Similar presentations:
Механические колебания и волны
1. Механические колебания и волны
2.
• Движения, обладающие той или инойстепенью повторяемости, называются
колебаниями.
• Если колебания повторяются через
равные промежутки времени, то они
называются периодическими.
• Гармонические – это такие колебания,
которые описываются периодическим
законом
х
(
t
)
A
sin(
t
)
0
0
или
х(t ) A cos( 0t 0 )
3. Дифференциальное уравнение гармонических колебаний:
2d x
2
x
0
0
2
dt
• Решение уравнения:
х(t ) A cos( 0t 0 )
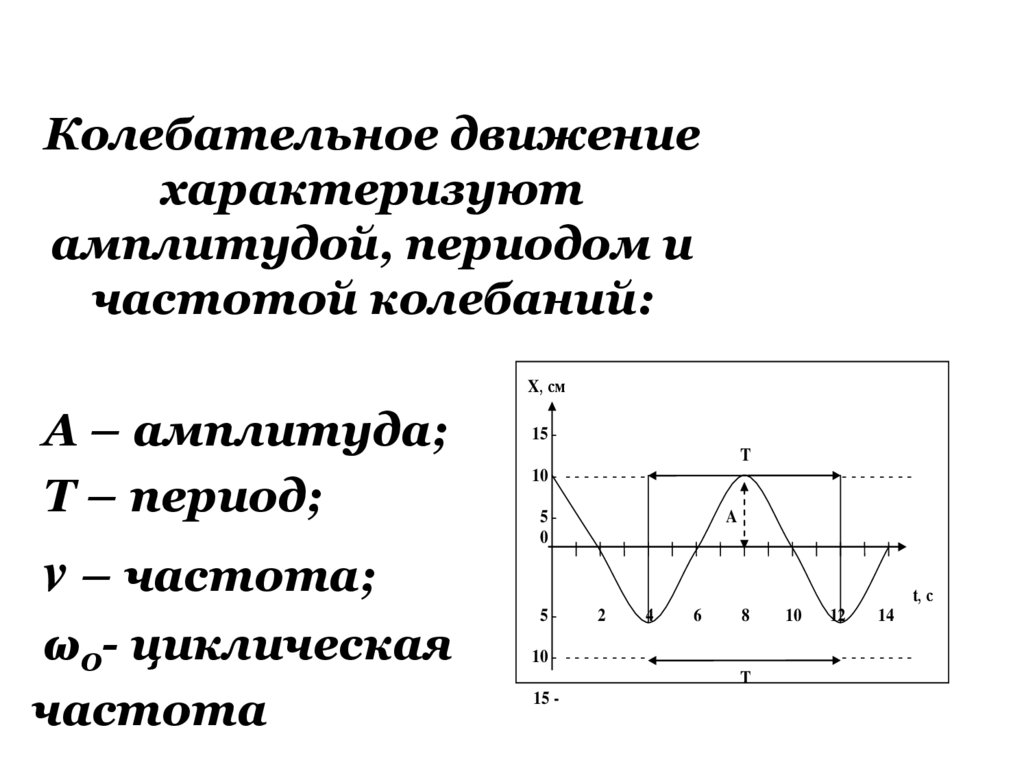
4.
Колебательное движениехарактеризуют
амплитудой, периодом и
частотой колебаний:
X, см
А – амплитуда;
Т – период;
Т
v = 0,125 Гц
15 T
10 - - - - - - - - - -
--------
50
A
v – частота;
ω0- циклическая
частота
t, с
5-
2
4
6
8
10 - - - - - - - - - -
12
14
-------T
15 -
10
5. Скорость колебательного движения:
max A 0dx
A 0 sin( 0t 0 )
dt
Ускорение колебательного
движения:
d d
a
( A 0 sin( 0t 0 ))
dt dt
2
2
A 0 cos( 0t 0 )
а max A
0
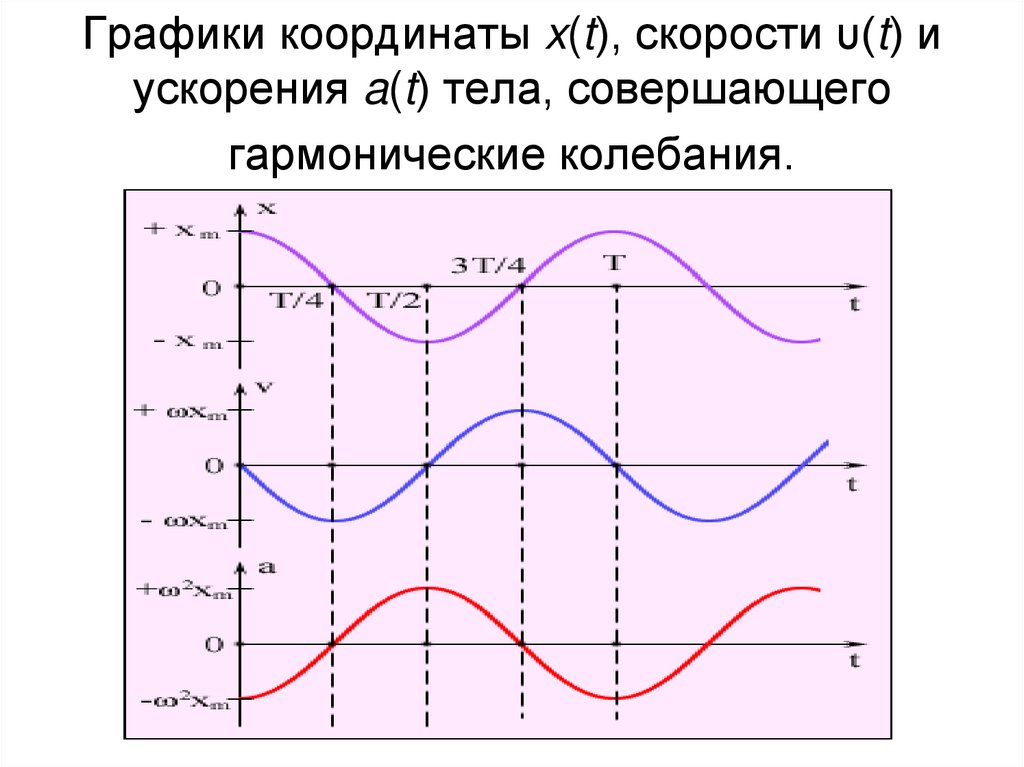
6. Графики координаты x(t), скорости υ(t) и ускорения a(t) тела, совершающего гармонические колебания.
7.
Затухающие колебания – это колебания,амплитуда которых, под действием
сил сопротивления, со временем
уменьшается, и через некоторый
промежуток времени становится
равной «0».
2
d x
dx
2
2
0 x 0
2
dt
dt
x A0 e
t
cos( t 0 )
8. График незатухающих колебаний
X, смА1 = А2 = А3 = . . . = const
График
10 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - незатухающих A 5 A
0
t, с
колебаний
1
3
5-
2
4
6
8
10
12
14
10 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - A2
График
затухающих
колебаний
X, см
А1 > A2 > A3 > . . . = 0
10 A1
50
A3
t, с
510
2
-
A2
4
6
8
10
12
14
9. Характеристики затухающих колебаний
Q NT
10.
• Декремент затухания θ - отношениезначений двух амплитуд, соответствующих
промежутку времени в один период
At
A0 e t
T
e
At T A0 e ( t T )
• Логарифмический декремент затухания:
ln
At
T
At T
11.
Свободные колебания –колебания, происходящие
под действием внутренних
сил в колебательной системе
за счёт первоначального
запаса энергии.
12.
Вынужденные колебания –колебания, происходящие под
воздействием внешних сил,
периодически изменяющихся с
течением времени.
2
F0
d x
dx
2
cos
t
2
x
0
2
m
dt
dt
13.
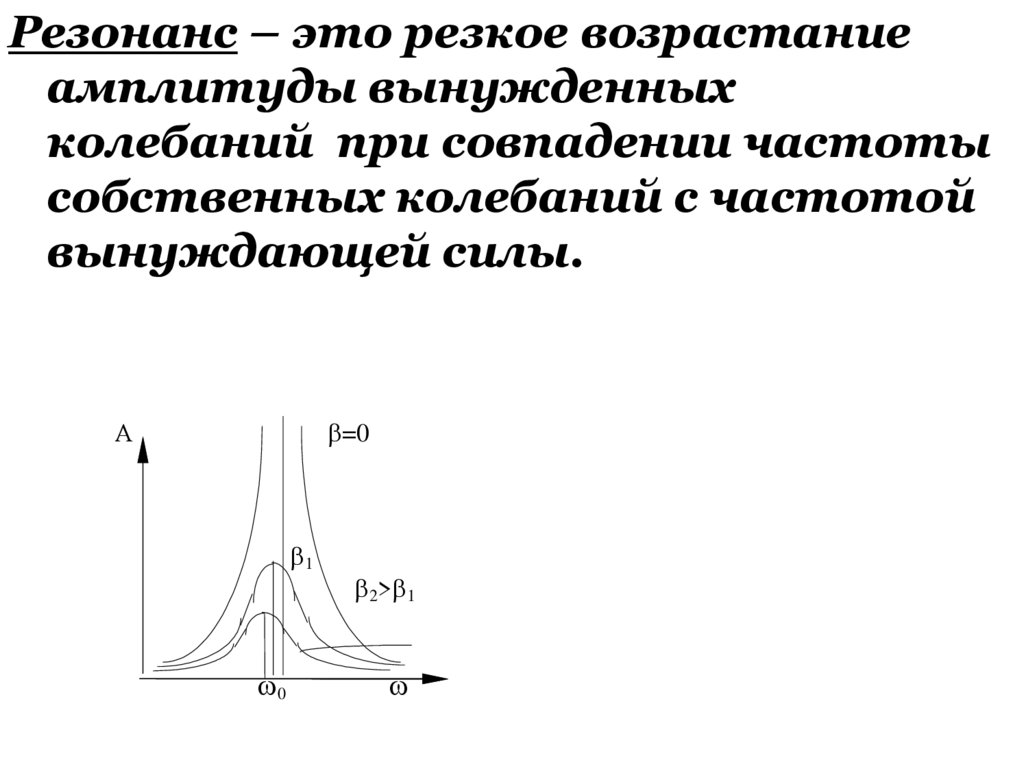
Резонанс – это резкое возрастаниеамплитуды вынужденных
колебаний при совпадении частоты
собственных колебаний с частотой
вынуждающей силы.
=0
А
1
0
Рис. 5.3.
A
2> 1
v
0
v
соб.
=
v
вын.
14.
• Пружинный маятник – тело массой m,подвешенный на пружине массой
которой можно пренебречь.
d2x
F m 2
dt
d2x
m 2 kx
dt
k /m
2
d x
2
x 0
2
dt
15.
20
Т
T 2
k
m
m
k
16.
Математический маятник – система, состоящая изневесомой и нерастяжимой нити, на которую
подвешена масса, сосредоточенная в точке.
d2x
F m 2
dt
F mg sin mg
d2x
2
x 0
2
dt
17.
20
Т
T 2
l
g
g
l
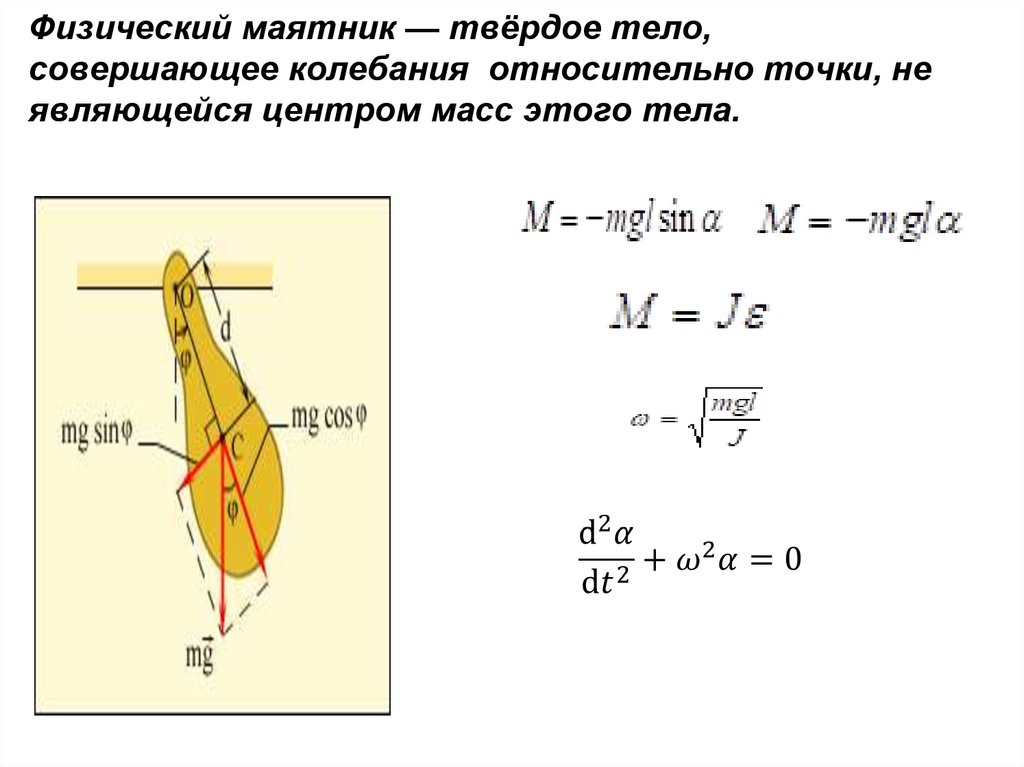
18. Физический маятник — твёрдое тело, совершающее колебания относительно точки, не являющейся центром масс этого тела.
19.
20
Т
mgl
I
T 2
I
mgl
20.
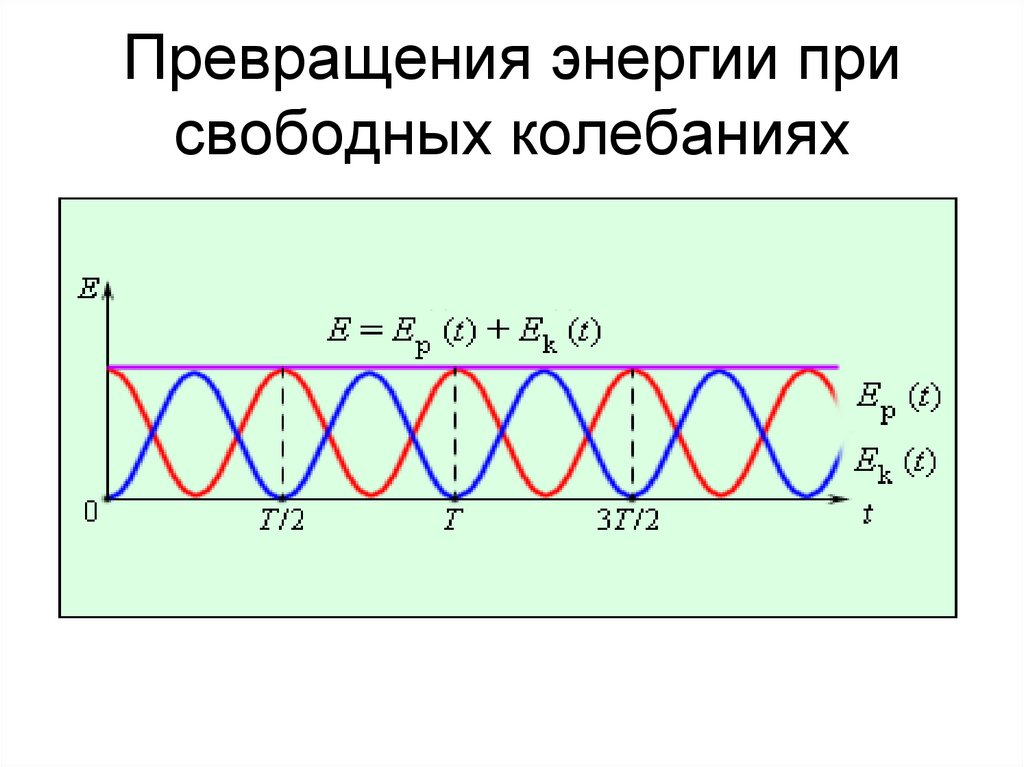
• При гармоническихколебаниях происходит
периодическое превращение
кинетической энергии в
потенциальную и наоборот.
21. Превращения энергии при свободных колебаниях
22.
2mv
1
2
2
2
EK =
m A cos t
2
2
23.
Полная энергия24. Сложение двух колебаний одного направления
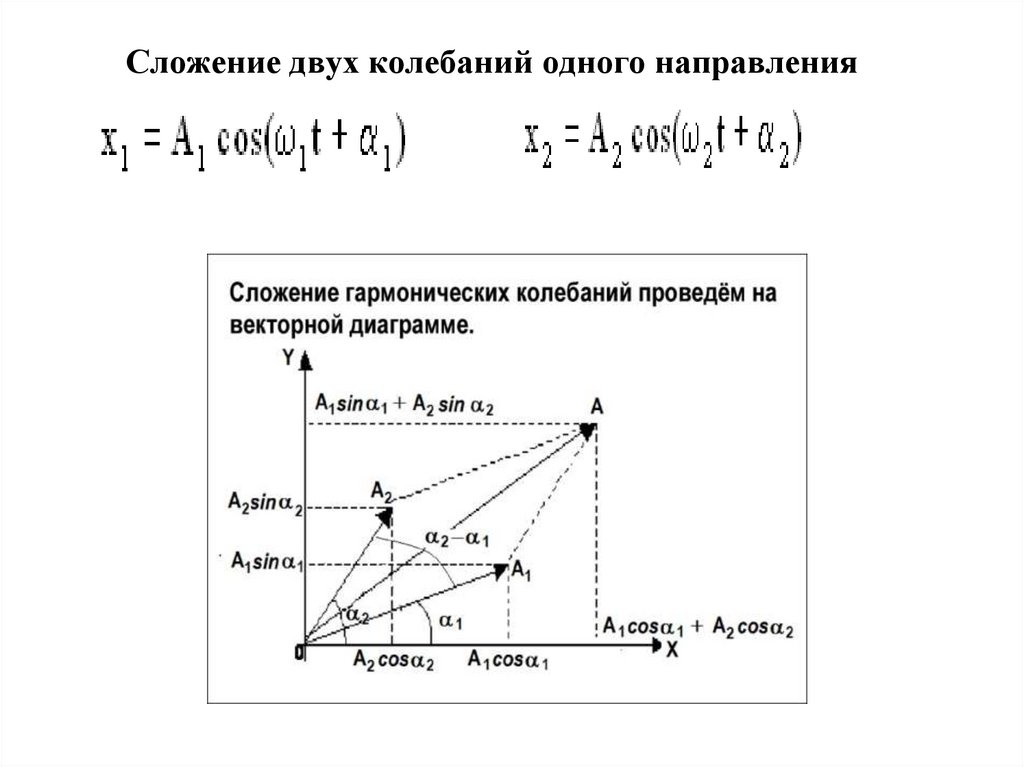
Сложение двух колебаний одного направления25.
A A A 2 A1 A2 cos( 2 1 )2
2
1
2
2
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2 cos 2
26.
Волна – процесс распространенияколебаний в пространстве.
y ( x, t ) A cos( (t
A cos( t kx )
x
) )
A
y ( x, t )
cos( t kr )
r
- волновое число-
27.
• Волновая поверхность — геометрическоеместо точек, колеблющихся в одинаковой
фазе (сферические, плоские).
• Волновой фронт — это поверхность, до
которой дошли колебания с одинаковой
фазой к данному моменту времени.
28.
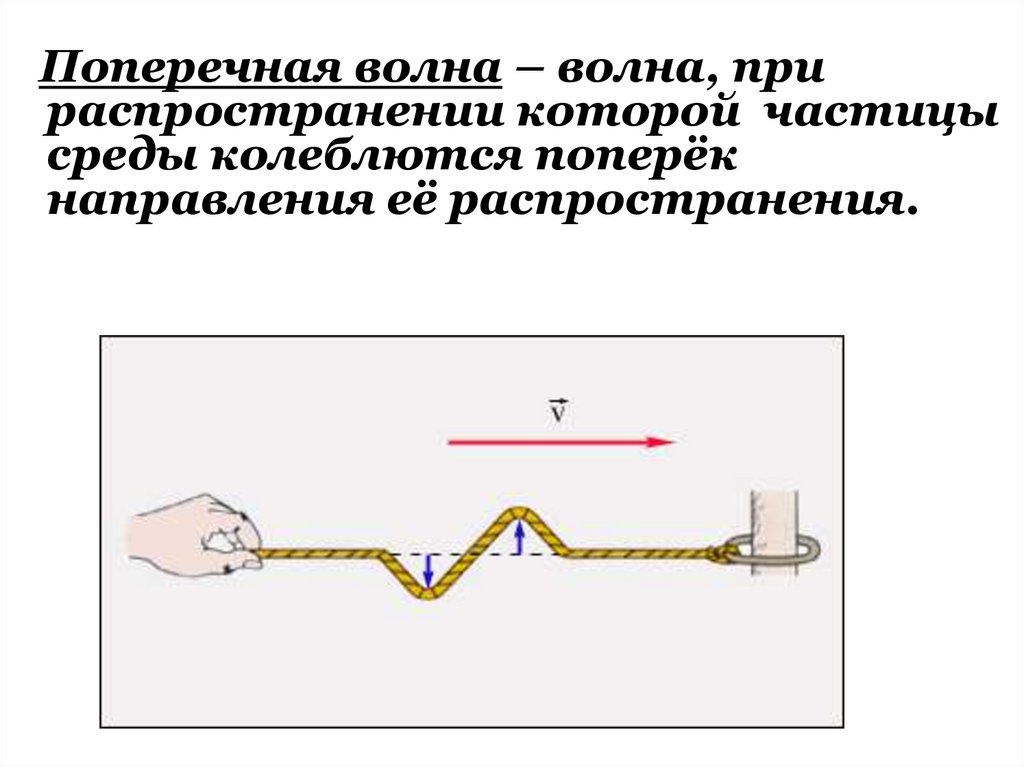
Поперечная волна – волна, прираспространении которой частицы
среды колеблются поперёк
направления её распространения.
29.
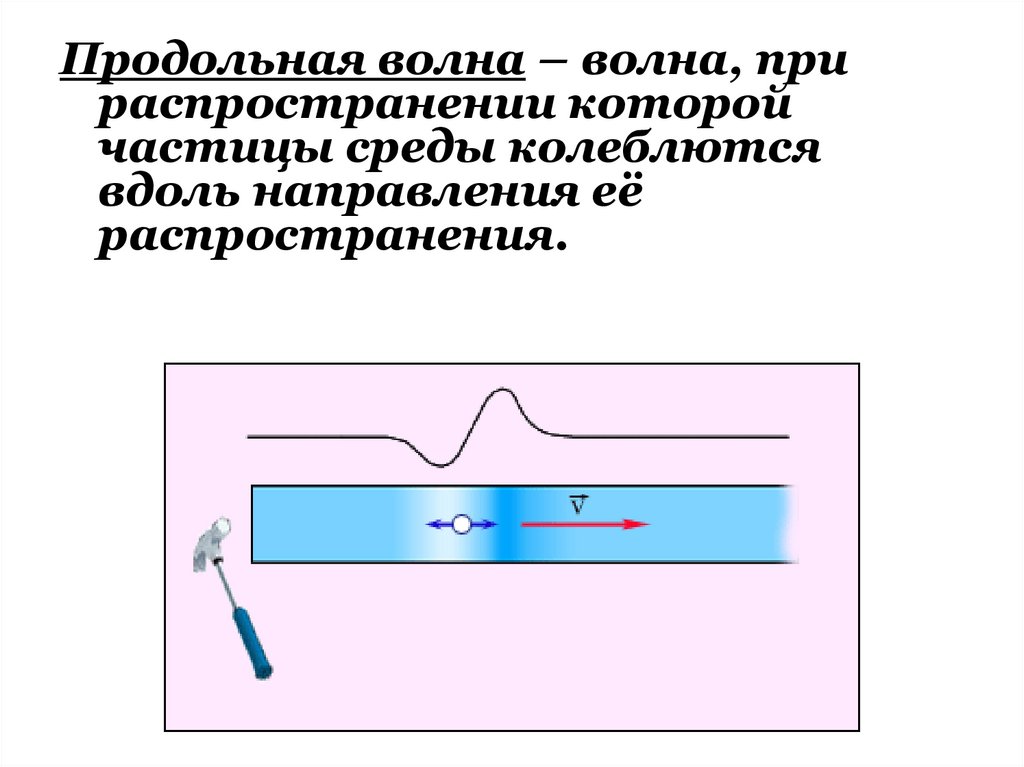
Продольная волна – волна, прираспространении которой
частицы среды колеблются
вдоль направления её
распространения.
30.
Скорость волны (v) - это скоростьраспространения колебаний в упругой
среде.
Длина волны ( λ ) – расстояние, на которое
распространяется волна за время, равное
одному периоду.
Т
• Волновое число k - характеризует скорость
изменения фазы в пространстве
2 2
k
vT v











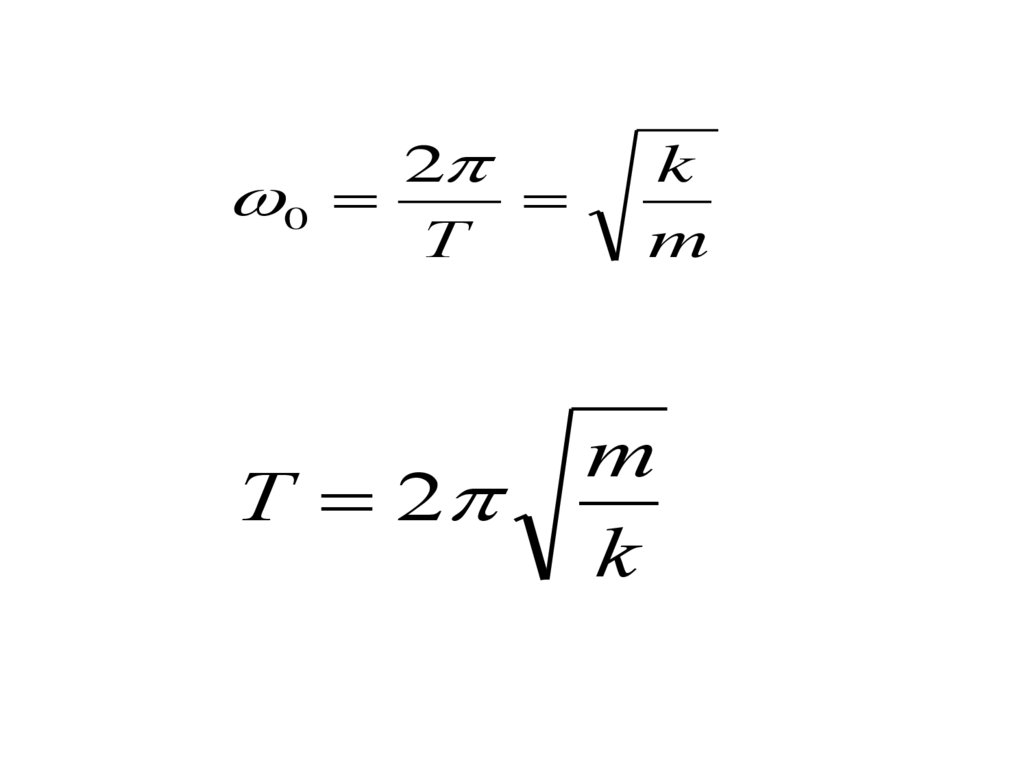

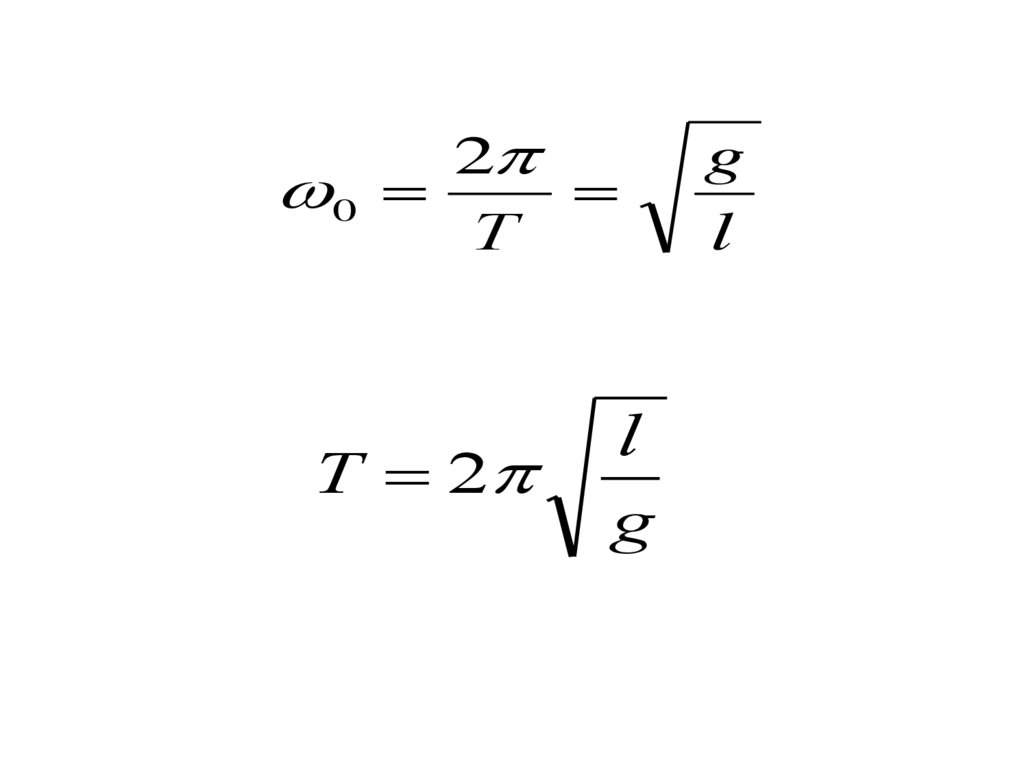
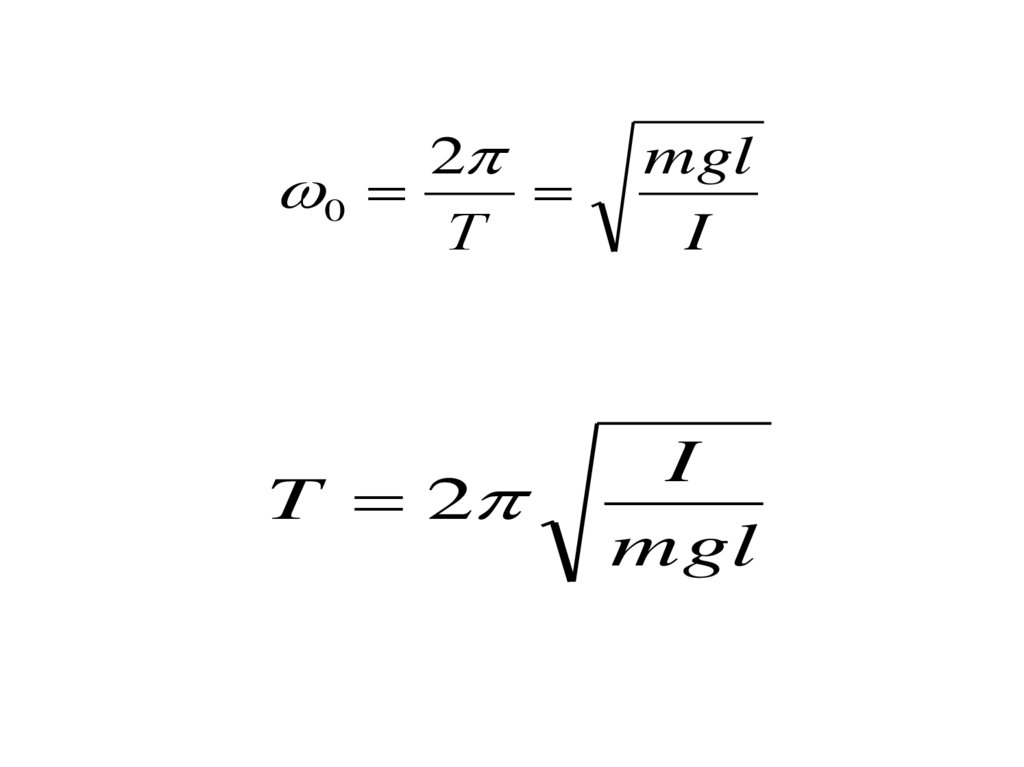







 physics
physics








