Механические колебания и волны

1.

4. Механические колебания и волны
1. Гармонические колебания и их характеристики.
2. Свободные незатухающие механические колебания.
3. Пружинный и математический маятники.
4. Свободные затухающие механические колебания.
5. Сложение гармонических колебаний.
6. Вынужденные колебания. Резонанс.
7. Механические волны.

2.

1. Гармонические колебания и их характеристики.
Колебания - процессы, характеризующиеся определенной повторяемостью во времени (периодические
изменения какой-либо величины).
Параметры гармонических колебаний
Период (Т) - время, в течении которого совершается одно полное колебание:
t
T ,
N
T 1c
N - число колебаний за время t
Частота колебаний - число полных колебаний, совершенных за единицу времени.
N
1
, Гц ,
t
c
1
1
T , .
T
Циклическая или круговая частота - число полных колебаний, совершенных за время 2 (единиц
времени):
2
2
Т

3.

Гармонические колебания - колебания, при которых изменение величины происходит по закону синуса
или косинуса:
x A cos( t 0 ),
х - значение изменяющейся величины;
А хmax - амплитуда колебаний, максимальное значение изменяющейся величины;
t 0 - фаза колебаний в момент времени t (угловая мера времени);
0 - начальная фаза
1рад
Скорость и ускорение при гармонических колебаниях:
dx
A sin t 0 , max A ,
dt
d
a
A 2 cos t 0 , a max A 2 .
dt
Гармонический осциллятор - колебательная система, совершающая гармонические колебания,

4.

2. Свободные незатухающие механические колебания:
Свободные или собственные колебания - колебания, которые совершает система около положения
равновесия после того, как она каким-либо образом была выведена из состояния устойчивого
равновесия и предоставлена самой себе.
Свободные или собственные колебания - это колебание, происходящие под действием возвращающей
силы:
а) для пружинного маятника - сила упругости;
б) для математического маятника - составляющая сила тяжести.
Если в системе отсутствуют силы трения, колебания продолжаются бесконечно долго с постоянной амплитудой и
называются собственными незатухающими колебаниями.

5.

6.

3. Пружинный и математический маятники
Пружинный маятник - материальная точка массой m, подвешенная на абсолютно упругой невесомой
пружине и совершающая колебания под действием упругой силы.
Fупр ma - 2 з-н Ньютона:
Fупр kx закон Гука,
d 2x d 2x k
d 2x
x 0
a 2 , kx m 2 ,
2
dt
m
dt
dt
k
02 , 0 циклическая частота собственных колебаний
m
d 2x
2
- дифференциальное уравнение свободных незатухающих
x
0
0
колебаний
dt 2
Решение этого уравнения:
x A cos( 0t )
2
m
T
2
Период колебаний пружинного маятника:
0
k

7.

Превращение энергии:
2 2
mА
0
m 2 mA2 02
2
Ek
sin 0 t 0 , E k max
;
2
2
2
2 2
2
m
kx2 kA2
kA
2
o А
Ep
cos 0 t 0 , E p max
,
2
2
2
2
k
02 k m 02
m
2 2
2 2
mA2 02
mA
mA
0
2
2
0
E Ek E p
sin 0 t 0
cos 0 t 0
,
2
2
2
E E k E p E k max E p max .
При гармонических колебаниях полная энергия системы
остается постоянной.

8.

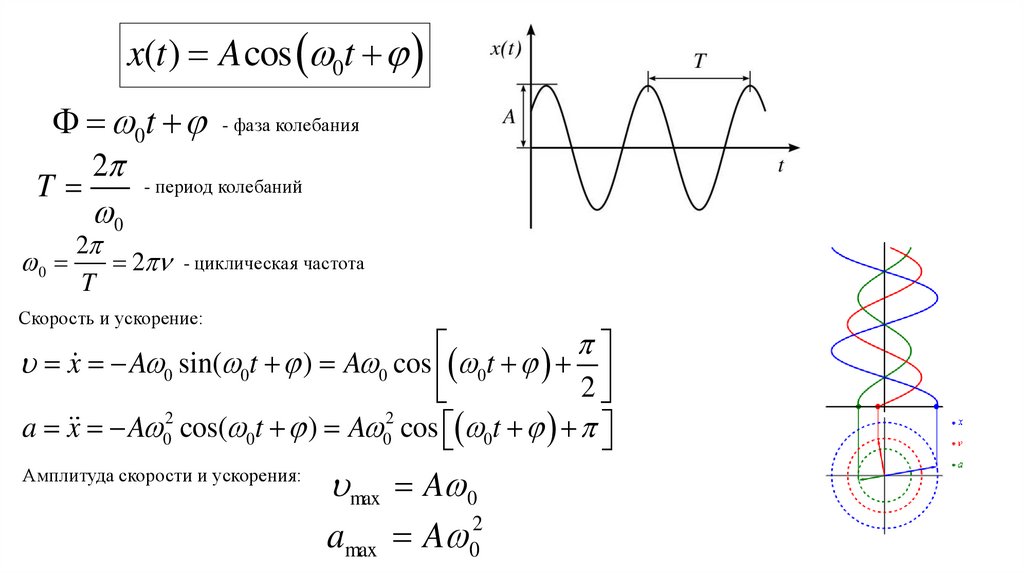
x(t ) A cos 0t
0t - фаза колебания
2
- период колебаний
T
0
2
0
2 - циклическая частота
T
Скорость и ускорение:
x A 0 sin( 0t ) A 0 cos 0t
2
a x A 02 cos( 0t ) A 02 cos 0t
Амплитуда скорости и ускорения:
max A 0
2
amax A 0

9.

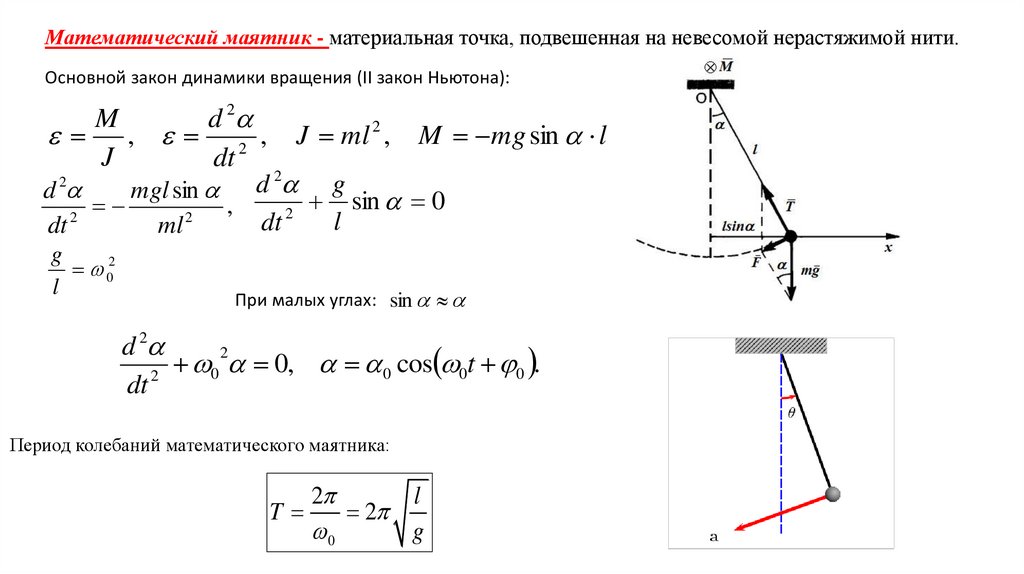
Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити.
Основной закон динамики вращения (II закон Ньютона):
M
d 2
, 2 , J ml 2 , M mg sin l
J
dt
2
2
d
g
d
mgl sin
sin 0
,
2
2
2
l
dt
dt
ml
g
02
l
При малых углах: sin
d 2
2
0 cos 0t 0 .
0 0,
2
dt
Период колебаний математического маятника:
T
2
l
2
0
g

10.

Пружинный и математический маятники являются гармоническими осцилляторами (как и
колебательный контур). Гармоническим осциллятором называется система, описываемая
уравнением:
d
2
0
0
2
dt
2

11.

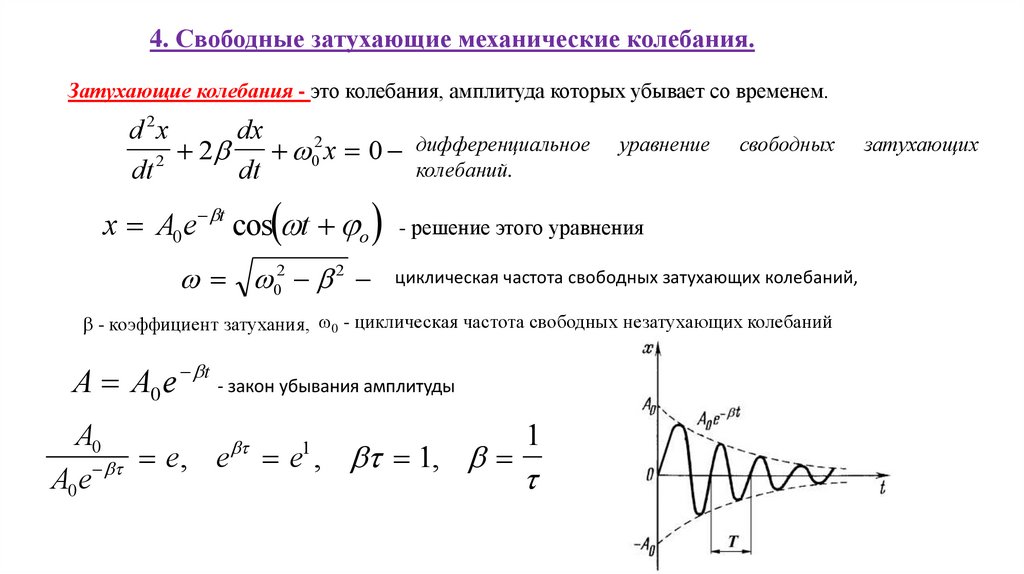
4. Свободные затухающие механические колебания.
Затухающие колебания - это колебания, амплитуда которых убывает со временем.
d 2x
dx
2
дифференциальное
2
x
0
0
колебаний.
dt 2
dt
уравнение
свободных
x A0e t cos t o - решение этого уравнения
02 2
циклическая частота свободных затухающих колебаний,
- коэффициент затухания, 0 - циклическая частота свободных незатухающих колебаний
А А0 е
t
- закон убывания амплитуды
А0
1
1
е е , 1,
е,
А0 е
затухающих

12.

Логарифмический декремент затухания - натуральный логарифм отношения двух амплитуд,
отличающихся друг от друга по времени на период:
A0
T
ln
ln e T
T
A0 e
x
Q1
Q2
x
0
Q1 Q2
0
t
t
N
T T
Q N
t
1
T
1
T T ,
N
- время релаксации - это время, за которое амплитуда уменьшается в e раз
Добротность - физическая величина, пропорциональная числу колебаний, в течение которых
амплитуда уменьшается в е раз

13.

5. Сложение гармонических колебаний: 1) одного направления и одинаковой
частоты; 2) взаимно перпендикулярных колебаний.
Векторная диаграмма - изображение гармонических колебаний графически в виде вектора на плоскости.
x A cos( t )
1. Сложение колебаний одного направления:
x1 A1 cos( t 1 ); x2 A2 cos( t 2 )
x = x1 + x2, 2 1
A2 A12 A22 2 A1 A2 cos 2 1
A12 A22 2 A1 A2 cos 2 1 ,
y y2
A sin 1 A2 sin 2
tq 1
1
x1 x2 A1 cos 1 A2 cos 2
a) 2 1 2k , (k 0,1,2...), A A1 A2 в фазе
b) 2 1 (2k 1) ,(k 0,1,2...), A A1 A2 в противофазе

14.

2. Сложение взаимно перпендикулярных колебаний:
Пусть оба колебания совершаются с одинаковой частотой:
x a1 cos t 1 ,
y a 2 cos t 2 .
Исключим время и свяжем х с у:
2
2
x y
2 xy
cos 2 1 sin 2 2 1
a1 a2 a1a2
a) 2 1 2k , k 0, 1, 2,...
y
2
2
x y
2 xy
0
a1 a 2
a1 a 2
x
x
y
0
a1 a 2
a2
y
x
a1
уравнение прямой
- уравнение эллипса

15.

б) 2 1 2k 1 , k 0, 1, 2,...
2
2
x y
2 xy
0,
a1 a 2
a1 a 2
a2
y x уравнение прямой
a1
y
x
в ) 2 1
2
2k 1 , k 0, 1, 2,...
y
y
a2
а
a1
x
x
x2 y2
2 1 уравнение эллипса
2
a1 a2
a1 a2 , x 2 y 2 a 2 - уравнение окружности
3. Если складываются взаимно перпендикулярные колебания с кратными периодами, то результирующее
движение происходит по сложным симметричным кривым, называемым фигурами Лиссажу. Их вид зависит от
соотношения периодов и разности фаз складываемых колебаний.

16.

Фигуры Лиссажу
x = acosωt
x = acosωt Y
Y
b
b
a
a
X
a X
a
b
y = bcos(2ωt+π/2)
y = bcos2ωt

17.

6. Вынужденные колебания. Резонанс.
Вынужденными называются колебания, которые совершаются
в системе под действием периодически
.
изменяющейся внешней силы.
Пусть внешняя сила изменяется по гармоническому закону:
F Fвозвр Fсопр ma ,
F F0 cos t
dx
d 2x
F0 cos t kx r m 2 ,
dt
dt
F0
d 2 x r dx k
x
cos t.
2
m dt m
m
dt
Пусть
F
r
k
2 , 02 , 0 f
m
m
m
d2x
dx
2
дифференциальное уравнение вынужденных гармонических колебаний
2
0 x f cos t
2
dt
dt
x A cos t решение дифференциального уравнения вынужденных гармонических колебаний
разность фаз колебаний х и F

18.

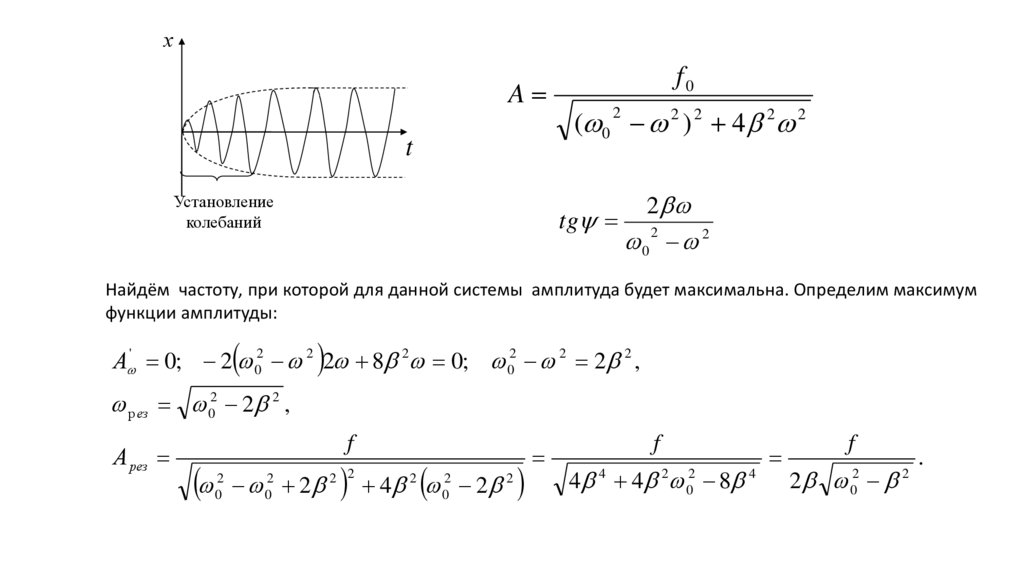
х
A
t
Установление
колебаний
f0
( 0 2 ) 2 4 2 2
2
tg
2
0 2 2
Найдём частоту, при которой для данной системы амплитуда будет максимальна. Определим максимум
функции амплитуды:
А ' 0; 2 02 2 2 8 2 0; 02 2 2 2 ,
р ез 02 2 2 ,
А рез
f
2 4 2
2
0
2
0
2 2
2
2
0
2
f
4 4 8
4
2
2
0
4
f
2
2
0
2
.

19.

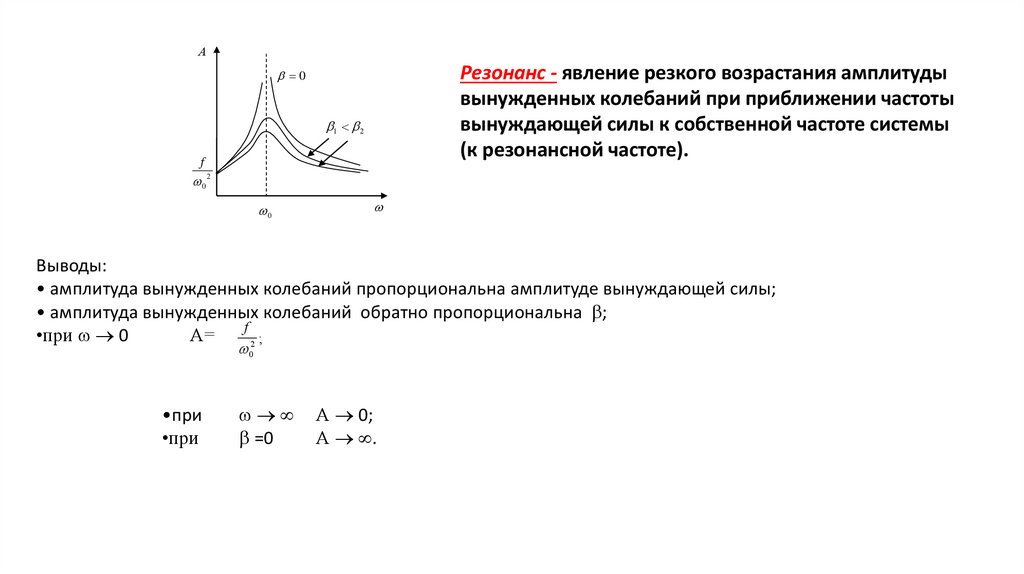
А
Резонанс - явление резкого возрастания амплитуды
вынужденных колебаний при приближении частоты
вынуждающей силы к собственной частоте системы
(к резонансной частоте).
0
1 2
f
0 2
0
Выводы:
• амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы;
• амплитуда вынужденных колебаний обратно пропорциональна ;
f
•при 0
А=
2 ;
0
•при
•при
=0
А 0;
А .

20.

7. Продольные и поперечные упругие волны. Принцип Гюйгенса.
Упругая волна - процесс распространения механических колебаний в упругой среде.
Этот процесс периодичен во времени и пространстве. При распространении волны частицы среды не
движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от
частицы к частице среды передается лишь состояние колебательного движения и его энергия.
Поэтому основное свойство всех волн - перенос энергии без переноса вещества.
Упругая волна называется продольной, если частицы среды колеблются вдоль направления
распространения волны
волны
частиц
Продольные волны возникают в твердых, жидких и газообразных телах,
в которых возникают упругие деформации при сжатии или растяжении.

21.

волны
частиц
Упругая волна называется поперечной, если частицы среды
колеблются перпендикулярно направлению распространения
волны.
Поперечная волна возможна в среде, где деформация сдвига вызывает упругие силы, т.е. в твердых телах.
Скорость продольных волн:
1
E
,
где
Е - модуль Юнга, - плотность среды
Скорость поперечных волн:
2
G
,
где - G - модуль сдвига.
1
E
2,5,
1,5
G
2
- для твердых веществ

22.

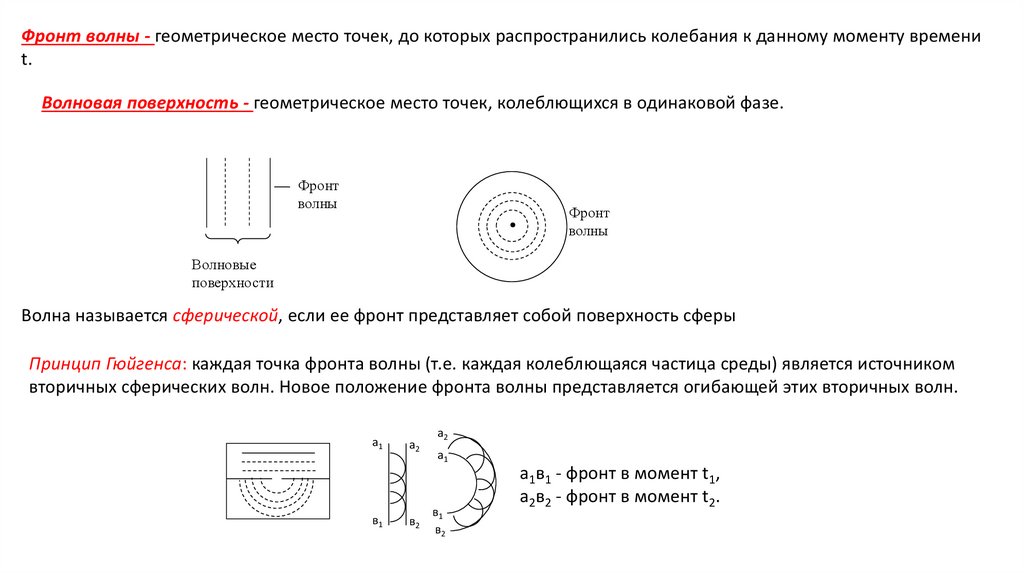
Фронт волны - геометрическое место точек, до которых распространились колебания к данному моменту времени
t.
Волновая поверхность - геометрическое место точек, колеблющихся в одинаковой фазе.
Фронт
волны
Фронт
волны
Волновые
поверхности
Волна называется сферической, если ее фронт представляет собой поверхность сферы
Принцип Гюйгенса: каждая точка фронта волны (т.е. каждая колеблющаяся частица среды) является источником
вторичных сферических волн. Новое положение фронта волны представляется огибающей этих вторичных волн.
а1
в1
а2
в2
а2
а1
в1
в2
а1в1 - фронт в момент t1,
а2в2 - фронт в момент t2.

23.

Уравнение плоской бегущей волны.
Бегущими называются волны, которые переносят в пространстве энергию.
Получим уравнение бегущей плоской волны, предполагая, что колебания носят гармонический характер, а ось Y
совпадает с направлением распространения волны.
Уравнение волны определяет зависимость смещения колеблющейся частицы среды от координат и времени.
В точке О смещение частицы от положения равновесия происходит по гармоническому закону:
X
В точке C:
В
0
y
С
Y
x A cos t ,
x A cos t ,
y
- время, за которое волна от точки O доходит до точки C,
- скорость распространения волны
y
x A cos t - уравнение плоской бегущей волны.
Если плоская волна распространяется не в положительном направлении оси Y, а в
противоположном направлении, то:
y
x A cos t .

24.

Длина волны - расстояние, на которое распространяется волна за период колебаний частиц среды:
T
T , , , 2
2 y
x A cos t
, x A cos t ky
1
k
2
- волновое число.
x A cos t ky 0
фаза плоской волны