Similar presentations:
Механические колебания и волны. Уравнение колебаний
1.
Механические колебанияи волны
2.
Механические колебания характеризуются величиной смещенияколеблющейся материальной точки (колеблющегося тела)
от положения равновесия.
Колебания, при которых смещение изменяется по закону синуса
или косинуса, называются гармоническими.
Если колебания происходят под действием внутренних сил системы
и начинаются тогда, когда систему выводят из положения равновесия,
то такие колебания называются свободными.
3.
Уравнение колебанийУравнение гармонических колебаний
x = Asin( 0t + 0),
где величины А, 0, 0 не зависят от времени.
Характеристики гармонических колебаний
А – амплитуда колебаний – максимальное смещение от положения
равновесия (максимальное значение изменяющейся величины).
Циклическая (или круговая) частота 0 – число полных колебаний,
совершаемых системой за промежуток времени 2 секунд.
Частота 0 – число полных колебаний, совершаемых системой за 1 с.
Период колебаний T0 – промежуток времени, за который совершается одно
полное колебание.
1
0
T0
2
0 2 0
T0
Фаза колебаний ( 0t + 0) определяет положение колеблющейся точки
(тела) в данный момент времени, 0 – начальная фаза, определяющая
положение колеблющейся точки в начальный момент времени при t = 0.
4.
Кинематические характеристикигармонических колебаний
x Asin( 0t 0 )
v x x A 0 cos( 0t 0 ) v0 cos( 0t 0 )
v0 A 0
ax v x – A 02sin( 0t 0 ) – a0sin( 0t 0 )
a0 A 02
ax = – ω02 x x = – ω02 x
ax – cx ω0 c
5.
Динамика гармонических колебанийmax Fрав x
ax = – ω02 x
Fрав x –m 02 x
Fx – kx
Гармонические колебания совершаются под действием
упругих или квазиупругих сил.
6.
Примеры расчета частоты колебанийв различных механических системах
Пример 1. Тело массой m подвешивается на пружине длиной l0
с коэффициентом упругости k . Определить период колебаний.
Fт Fупр 0 , mg k l
l mg / k
l l0 l l0 mg / k
7.
ma Fт Fупрна ось X : max mg – Fупр
Fупр k ( l x)
max – kx
k
ax x
m
k
k
2
0
0
m
m
m
T0 2
k
8.
Пример 2. Математический маятник представляет собойтело, которое можно считать материальной точкой,
подвешенное на длинной невесомой нерастяжимой нити.
Длина нити l. Определить период колебаний математического
маятника T.
F mgtg
x / l sin tg
F Fx mg , Fx Тsin
x
max mg
l
g
g
ax x ω02
ω0
l
l
g
l
T0 2
l
g
9.
Пример 3. В жидкости плотностью ж плавает цилиндр высотой h.Если цилиндр поглубже погрузить в жидкость или, напротив,
немного вытащить из жидкости, то после того, как его отпустят,
цилиндр начнет колебаться. Плотность материала, из которого сделан
цилиндр, м. Определить частоту колебаний цилиндра.
Fвыт Fт , ж Sx0 g ρ м Shg
x0 =
ρм
h
ρж
max – ж Sgx m мV
м hSax – ж Sgx
ρж g
ax = –
x
ρм h
ρж g
ω0 =
ρм h
10.
Примеры решения задачЗадача 1. Колебания материальной точки происходят относительно
положения равновесия по закону: x = A sin ( t) с периодом 12 с.
Определите, за какой наименьший промежуток времени t1 точка
удалится от положения равновесия на расстояние, равное половине
амплитуды. За какой промежуток времени t2 она пройдет оставшуюся
часть пути до максимального отклонения?
Решение.
В момент времени t1 смещение А/2 = А sin ( t1)
in ( t1) = 1/2
t1 = π/6 2 t1/T = π/6
t2 =T/4 – Т/12 = 2 c
t1 = Т/12 = 1 c
11.
Задача 2. x = 0,3 sin (t + 0,5) м. Определите: 1) амплитуду; 2) периодколебаний; 3) начальную фазу, а также смещение и ускорение через
0,25 с после начала колебаний.
Решение.
x Asin( t + 0 )
x 0,3 sin [ t 0,5 ] м
А 0,3 м , с –1 , 0 0,5
2 2
T
2с
x 0,3sin 0, 25 0,5 м 0, 21 м
ax – 2 x – 2,1 м / с 2
12.
Задача 3. В U-образной трубке находится столбик жидкости длиной l.При кратковременном изменении давления жидкости в одном из колен
уровни жидкости сместились, и столбик начал колебаться.
Определите частоту колебаний. Трением о стенки пренебречь.
Решение.
Fд pS gS 2 x
max – g 2Sx
m lS
2g
ax
x
l
2g
l
13.
Задача 4. На горизонтальной плите находится груз. Плита колеблетсяс частотой , совершая по вертикали гармонические колебания.
При каких амплитудах колебания груз не оторвется от плиты?
Решение.
max mg – N
N 0 x A
x Asin(ωt) , ax – 2 Asin(ωt)
x A ax – 2 А – g , 2 A g
А g / 2
14.
Задача 5. Шарик массой m подвешен на двух пружинах одинаковойдлины, но с разными упругими свойствами. Коэффициенты жесткости
пружин k1 и k2. Определите частоту колебаний шарика в двух случаях,
показанных на рисунках. Массами пружин можно пренебречь.
Решение.
mg – ( k1 k2 )x0
Fупр x – k1 k2 x0 x
max – k1 k2 x0 x mg
max – k1 k2 x
k1 k2
a
x
x
m
k1 k2
m
15.
mg k2 x20max – k2 ( x20 x2 ) mg
max – k2 x2
ах x x x1 x2
k1 x10 x1 k2 x20 x2
k1 x10 k2 x20
k1 x
x
x2
k
1 2 k1 k2
k1
k1k2
ax
x 2
k1 k2 m
k1k2
k1 k2 m
16.
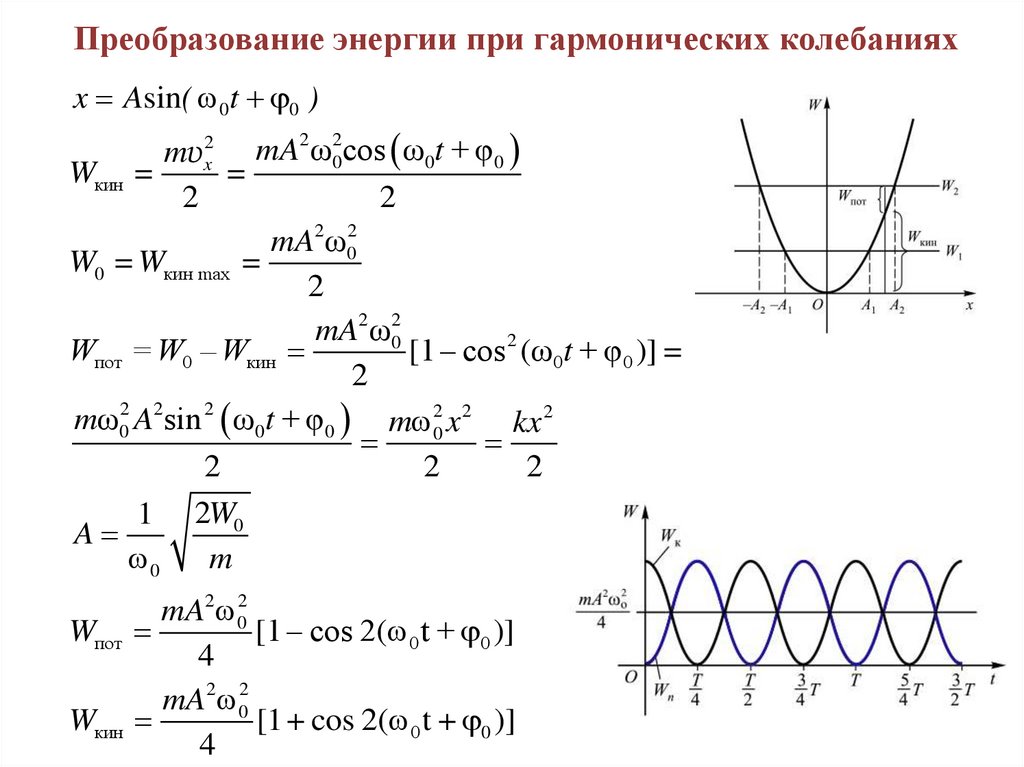
Преобразование энергии при гармонических колебанияхx Asin( 0t 0 )
mυ x2 mA ω0 cos ω0t + φ 0
Wкин =
=
2
2
mA2 ω02
W0 = Wкин max =
2
mA2 ω02
Wпот = W0 – Wкин
[1 – cos 2 (ω0t + φ 0 )] =
2
mω02 A2sin 2 ω0t + φ 0 m 02 x 2 kx 2
2
2
2
1 2W0
A
0
m
2
2
mA2 02
Wпот
[1 – cos 2( 0 t + 0 )]
4
mA2 02
Wкин
[1 + cos 2( 0 t + 0 )]
4
17.
Сложение колебаний, направленных вдоль одной прямойx1 A1 sin ( 0 t) , x2 A2 sin ( 0 t + )
x x1 x2 A1 sin ( 0 t) A2 sin ( 0 t + )
2 n,n 0, 1, 2,
x A1 A2 sin ( 0 t)
( 2n 1 )
x A1 A2 sin ( 0 t)
A1 – A2 A A1 A2
18.
Задача 9. Шарик массой 10 г совершает гармоническиеколебания с амплитудой А = 0,2 м и периодом T = 4 с.
В момент t0 = 0 смещение шарика x = A. Найдите кинетическую
и потенциальную энергию в момент времени t1 = 1 с.
Решение.
2
mvmax
Wкин max W0
2
2
vmax A A
T
mA2 4 2 2mA2 2
Wкин max W0
2
2T
T2
19.
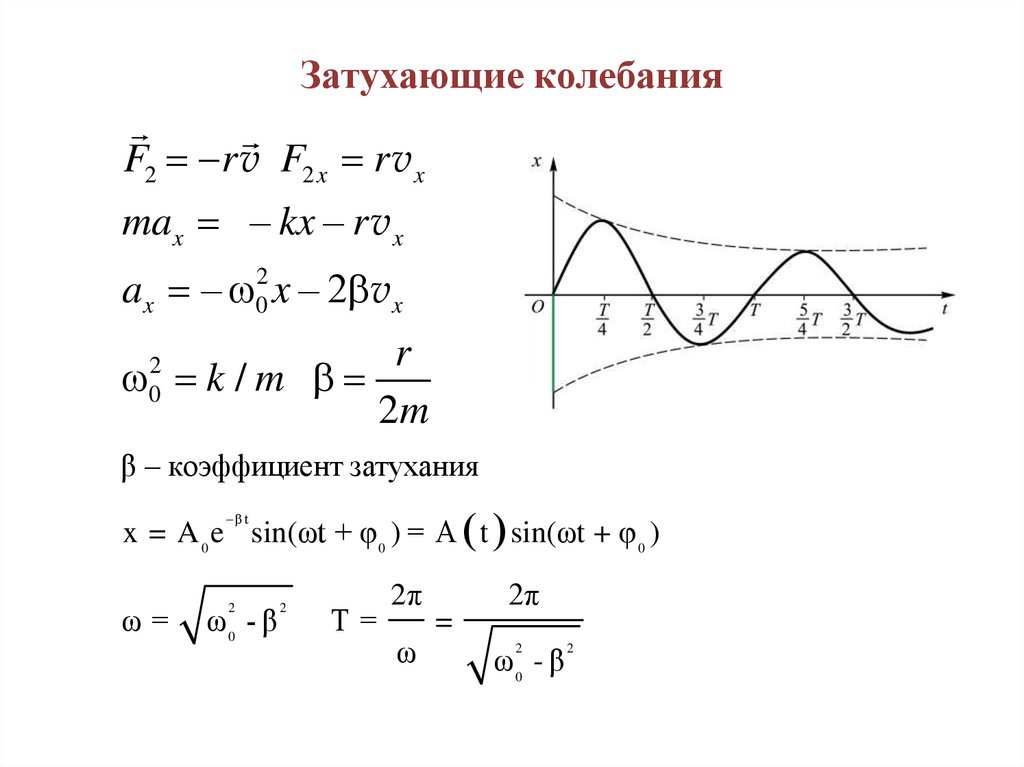
Затухающие колебанияF2 r v F2 x r v x
max – kx – r v x
ax – 02 x – 2 v x
r
k/m
2m
2
0
β – коэффициент затухания
x = A 0 e sin(ωt + φ 0 ) = А t sin(ωt + φ 0 )
–βt
ω=
2
ω0 - β
2
T=
2π
ω
=
2π
2
ω0 - β
2
20.
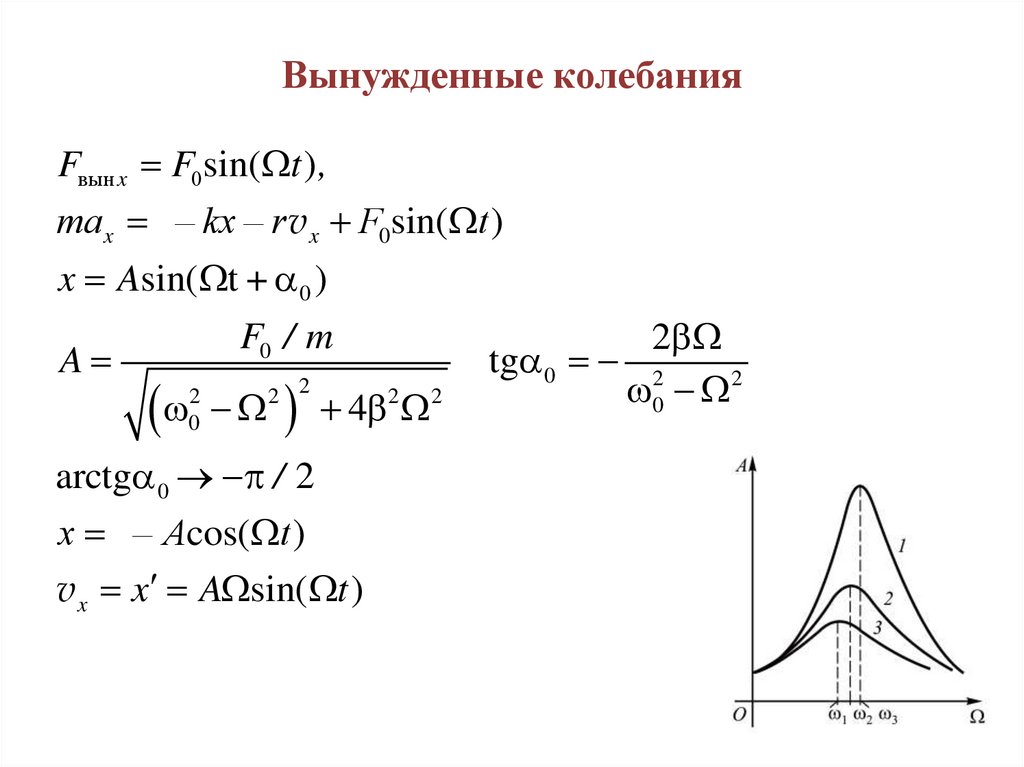
Вынужденные колебанияFвын x F0sin( t ) ,
max – kx – r v x F0sin( t )
x Asin( t + 0 )
A
F0 / m
2 2
4
2
0
2 2
arctg 0 / 2
x – Acos( t )
v x x A sin( t )
2
tg 0 2
0 2
21.
Задача 11. При какой скорости поезда маятник длиной l,подвешенный к потолку вагона, начнет сильно раскачиваться.
Расстояние между стыками рельсов равно s.
Решение.
s
1 1 g
0
v
T 2 l
0
l
v s / 2
g
22.
Задачи для самостоятельного решения.1. Во сколько раз изменится период колебаний математического маятника при
увеличении длины нити в 2 раза?
2. Математический маятник, длина нити которого равна 1 м, находится в лифте,
движущемся с ускорение g/2, направленным вниз.
Чему равен период колебаний маятника?
3. Шарик на пружине совершает гармоническое колебание с амплитудой А. Какое
расстояние проходит шарик за половину периода?
4. Чему равна начальная фаза в уравнении x = А sin ( t + 0), если при
t = 0 x = A/2.
5. Во сколько раз изменится период колебаний шарика, подвешенного на пружине, если
пружину разрезать пополам и его подвесить к одной из половин?
6. Имеется два одинаковых математических маятника. Нити маятников отводятся на
малые углы и 2 и одновременно отпускают. Какой из маятников первым пройдет
положение равновесия?
23.
Спасибо за внимание24.
Механические волны25.
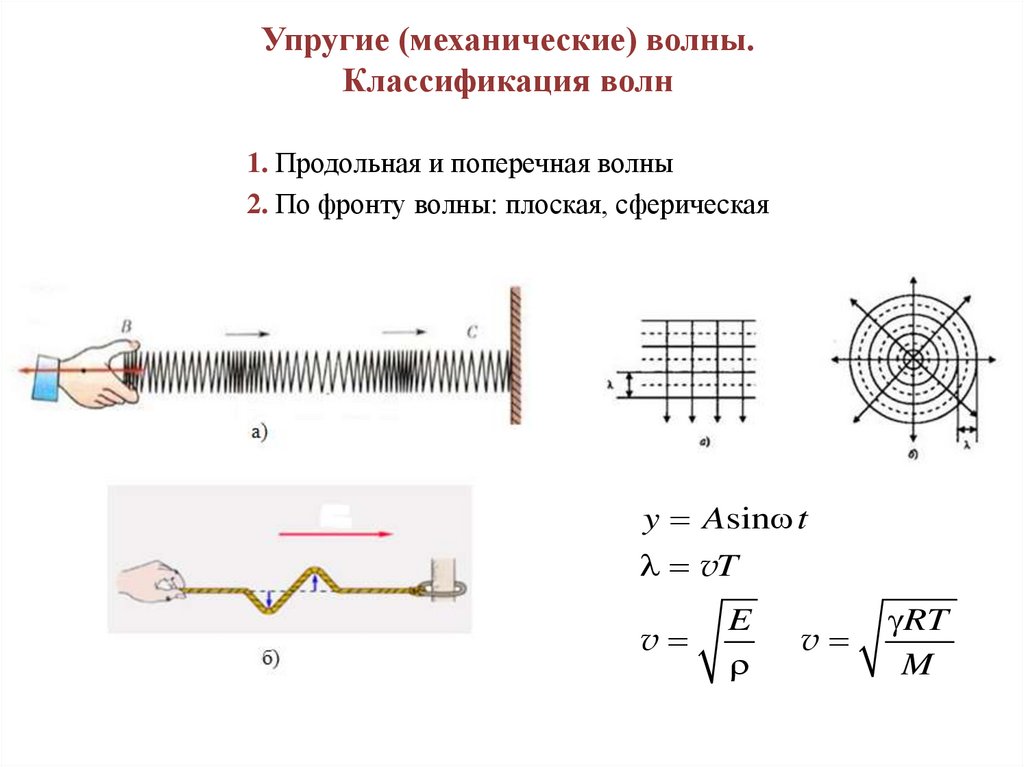
Упругие (механические) волны.Классификация волн
1. Продольная и поперечная волны
2. По фронту волны: плоская, сферическая
y Asin t
vT
v
E
v
RT
M
26.
Кинематическое уравнение плоской бегущей волныy0 Asin ( t ),
yМ Asin ( t )
xM
t = t τ = t
v
x
yM Аsin t M
v
x
y Asinω t
v
Длина волны – расстояние между точками, разность фаз колебаний
в которых, равна 2π
Скорость волны и скорость колебаний
x
u y y A cos t
v
27.
Интерференция волнИнтерференция – явление наложения волн в пространстве с
образованием устойчивой во времени картины максимумов и
минимумов амплитуды колебаний частиц среды.
Когерентными называются источники, вызывающие в каждой точке
пространства колебания c одинаковой частотой и разность фаз которых
остается постоянной во времени.
t l
t l
y1 = A1sin2 1 y2 = A2sin2 2
T
T
l l
2
1 – 2 2 1 2
l
2 n, n 0, 1, 2,
l
2
2 n, l nl A A1 A2
( 2n 1 ) l (2n 1) A A1 A2
2
28.
Когерентные источники :W ~ A2 4 A12 максимумы ( А1 А2 )
W 0 минимумы
4 A12 0
W
2 A12
2
Некогерентные источники :
W1 ~ A12 W2 ~ A22
W W1 W2 ~ A A Аср
2
1
А1 А2 ,W
2 A12
2
2
2
29.
Стоячая волнаt x
t x
yпр Asin2π yобр Asin2
T
T
2
yст yпр yобр 2 Аcos
x sin( t)
кинематическое уравнение стоячей волны
2
Аст 2 Аcos
x
x
2 n n 0 , 1, 2
x n
Аст 2 А пучности волны
2
x
2 (2n 1)
x (2n 1)
2
4
узлы стоячей волны
30.
Сравнение стоячей и бегущей волнБегущая волна
Стоячая волна
2 x
sinωt
Уравнение
t
x
y Asin 2
T
Амплитуда
Одинакова во всех
точках и равна А.
Зависит от положения
колеблющейся частицы
(воздуха, резинового шнура
и т. д.)
0 Аст 2А
Фаза
Зависит от положения
колеблющейся точки
Одинакова между двумя
соседними узлами
y 2 Аcos
31.
L = /2, = 2L. 1 – основной тон.Частоты колебаний, возбужденных этими волнами,
кратны 1: n 1,
n = 1, 2, 3, …
Эти частоты, на которых возникают стоячие волны,
называются собственными или резонансными частотами.
,
v
4 L, 1
4L
v
резонансные частоты равны n n n 1
4L
n 1, 2, 3,
32.
Звуковые волныν –16 Гц – 20 кГц 16 Гц
ν < 16 Гц – инфразвук, ν > 20 кГц – ультразвук
t x
y Asin 2
T
Вещество
Скорость
Вещество
звука, м/с
Скорость
звука, м/с
Воздух (20 С)
343
Вода
1440
Воздух (0 С)
331
Железо
5000
Водород
1300
Стекло
4500
Гелий
1005
Древесина
4000
v 331 + 0,6t C (м/с)
33.
Объективные и субъективные характеристики звукаОбъективные
характеристики звука
Субъективные
характеристики звука
Интенсивность волны
Громкость
Частота
Высота тона
Набор гармоник
Окраска звука (тембр,
качество звука)
I = 10–12 Вт/м2 (порог слышимости)
I = 1 Вт/м2 (порог болевого ощущения)
34.
Задача 1. Источник частотой 1000 Гц и амплитудой А = 0,5 ммвозбуждает в упругом шнуре волны длиной = 0,35 м.
Найдите:
1) скорость распространения колебаний в шнуре v,
2) максимальную скорость колеблющихся точек шнура umax.
Решение.
1)v = = 0,35 1000 м/с = 350 м/с.
2) umax = A = A 2 = 5 10–4 2 1000 м/с = м/с.
35.
Задача 2. В среде распространяется волна со скоростью υ = 720 м/с причастоте источника 600 Гц. Определите разность фаз колебаний в двух
точках, отстоящих друг от друга на расстоянии x = 0,2 м.
Решение.
2
yM Asin t xM Asin М
2
yN Asin t xN Asin N
2
2
N – M ( xM – xN ) x
2 x
v
3
36.
Задача 3. Труба длиной 1 м открыта с обоих концов. Определитесамую низкую резонансную частоту в трубе, скорость звука в воздухе
равна 330 м/с.
Решение.
vзв
max l / 2
vзв vзв
1
165 Гц
2l
37.
Задача 4. Выстрел произведен вертикально вверх. Какова начальнаяскорость пули v0, если звук выстрела и пуля достигают одновременно
высоты h = 850 м? Скорость звука в воздухе υзв = 340 м/с.
Решение.
gt22
y1 vзвt1 y2 v0t2 –
2
y1 y2 h, t1 t2 t
h
t
vзв
v0 h gh 2
h
2
vзв 2vзв
gh 2
h 2 vзв
2vзв
gh
м
v0
1 2 vзв 352
h
с
2vзв
38.
Задачи и тесты для самостоятельного решения1. Возбуждается поперечная волна в упругом стержне. Как изменится
скорость распространения волны в стержне и амплитуда колебаний в
разных точках стержня при увеличении периода колебаний в
источнике? При этом энергия источника волн постоянна.
Для каждой величины выберите соответствующий характер
изменения:
1) увеличится;
2)уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической
величины.
Скорость распространения волны
Амплитуда колебаний
39.
2. С берега высотой 5 м горизонтально бросают камень со скоростью 10 м/с.Скорость бегущей волны, образующейся на поверхности воды, равна 6 м/с. Через
какой промежуток времени с момента броска камня волна дойдет до берега?
3.По длинному шнуру начинает бежать волна со скоростью 200 м/с. Амплитуда
колебаний точек шнура равна 5 см, частота колебаний 5 Гц. Запишите уравнение
бегущей волны, взяв за начало отсчета координаты конец шнура (х = 0), а начало
отсчета времени — с момента начала колебаний этого конца.
x
4. Уравнение волны имеет вид s 0, 2sin 20 t
. Определите амплитуду и
300
период колебаний точек среды, длину волны и запишите уравнение колебаний в
точке, находящейся на расстоянии 15 м от источника.
5. Волна распространяется вдоль прямой со скоростью 50 м/с. Определите разность
фаз колебаний в точках, находящихся на этой прямой и отстоящих на расстоянии 50
см друг от друга. Период колебаний 0,05 с.
6. Чему равна длина струны, если при ее укорачивании на 10 см частота колебаний
увеличивается в 1,5 раза?






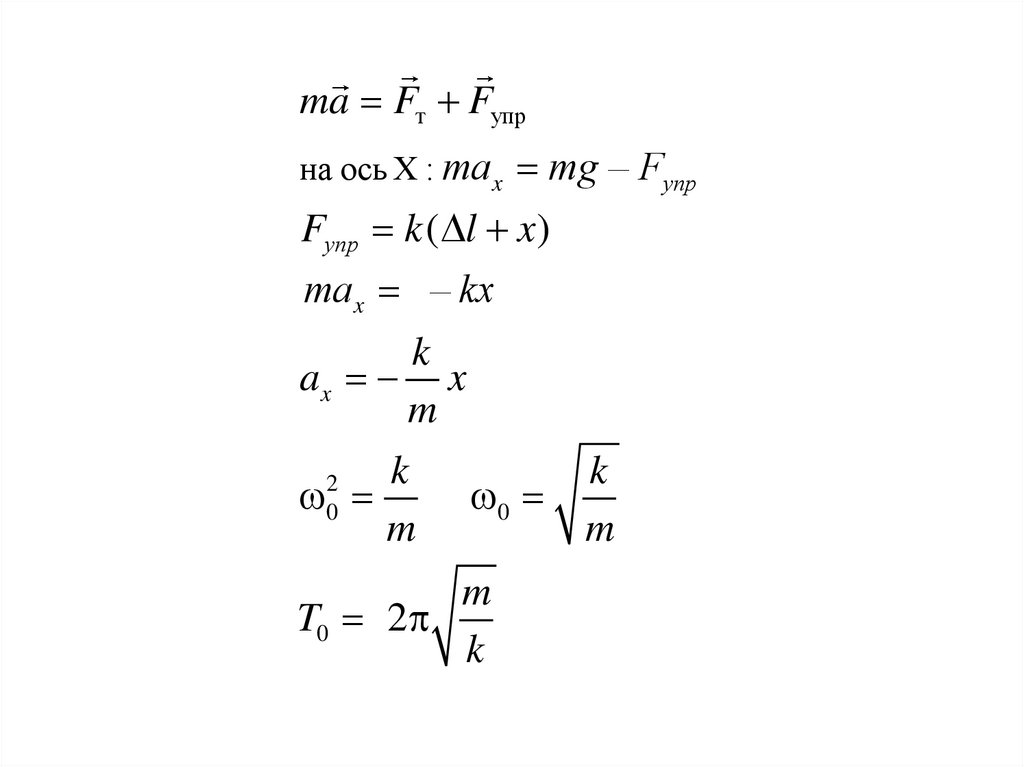





























 physics
physics








