Similar presentations:
Механические колебания. Вынужденные колебания. Сложение колебаний. Разложение и синтез колебаний. (Лекция 8)
1. Лекция 8
12.
Контрольный вопросГруз массы m, прикрепленный к пружине,
отведен в положение x = А и отпущен.
За полный цикл колебаний груз преодолеет путь, равный:
а) А/2,
б) А,
в) 2А,
г) 4А.
г) 4А.
2
3.
Содержание предыдущей лекцииМеханические колебания
• Гармонические колебания: амплитуда, частота и фаза
колебаний.
• Кинематическая и векторная форма представления
колебаний.
• Идеальный гармонический осциллятор. Уравнение
идеального осциллятора и его решение.
• Свободные затухающие колебания.
3
4.
Содержание сегодняшней лекцииМеханические колебания
• Вынужденные колебания. Время установления вынужденных
колебаний и его связь с добротностью.
• Сложение колебаний. Векторное описание сложения колебаний.
Биения, фигуры Лиссажу.
• Разложение и синтез колебаний.
• Понятие о спектре колебаний.
• Связанные колебания.
• Волновое движение.
• Уравнение волны в газах, жидкостях и твердых телах.
• Плоская механическая волна.
• Длина волны, волновое число, фазовая скорость.
• Одномерное волновое уравнение.
4
5.
РезонансРазрушение моста в результате резонанса.
5
6.
Время установления вынужденныхколебаний и его связь с добротностью
Процесс установления колебаний – переходный процесс.
Зависимость процесса установления колебаний от:
• соотношения между частотами собственных
колебаний и вынуждающей силы,
• сдвига по фазе между ними.
6
7.
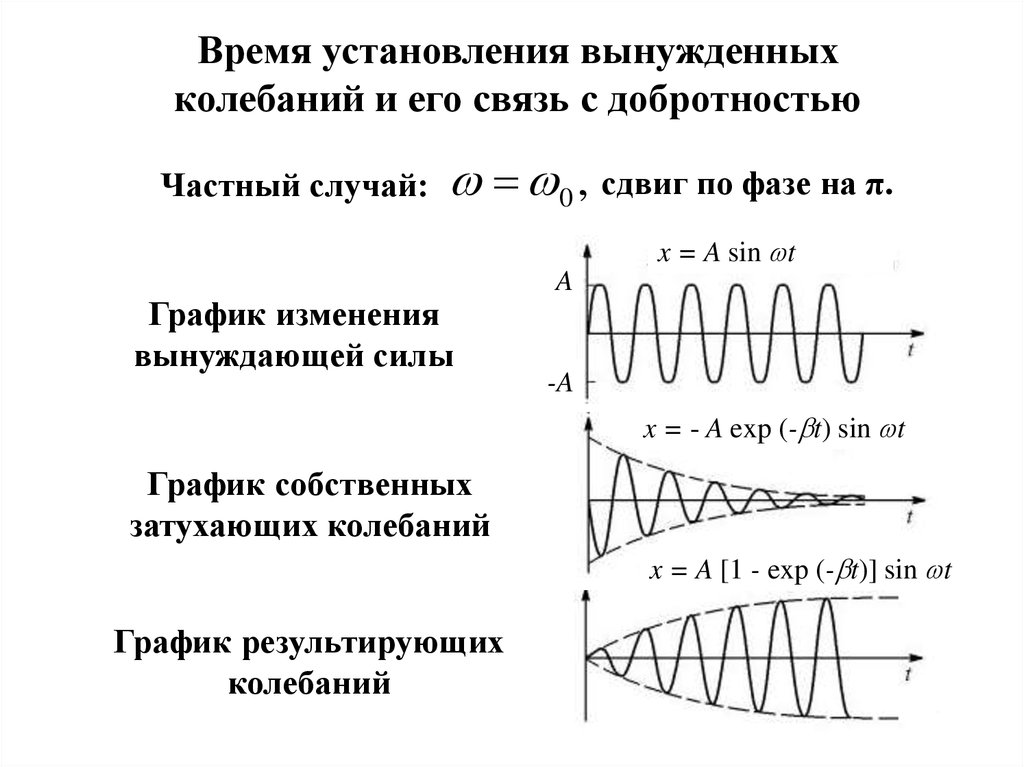
Время установления вынужденныхколебаний и его связь с добротностью
Частный случай:
0 , сдвиг по фазе на π.
x = A sin t
График изменения
вынуждающей силы
A
-A
x = - A exp (- t) sin t
График собственных
затухающих колебаний
x = A [1 - exp (- t)] sin t
График результирующих
колебаний
7
8.
Время установления вынужденныхколебаний и его связь с добротностью
Частный случай:
0 , сдвиг по фазе на π.
Завершение процесса:
только вынужденные колебания.
Случай малого затухания собственных колебаний:
результирующее колебание - синусоидальное колебание,
амплитуда которого медленно нарастает со временем.
Совпадение характерного времени установления колебаний
с временем жизни собственных затухающих колебаний
в той же системе.
8
9.
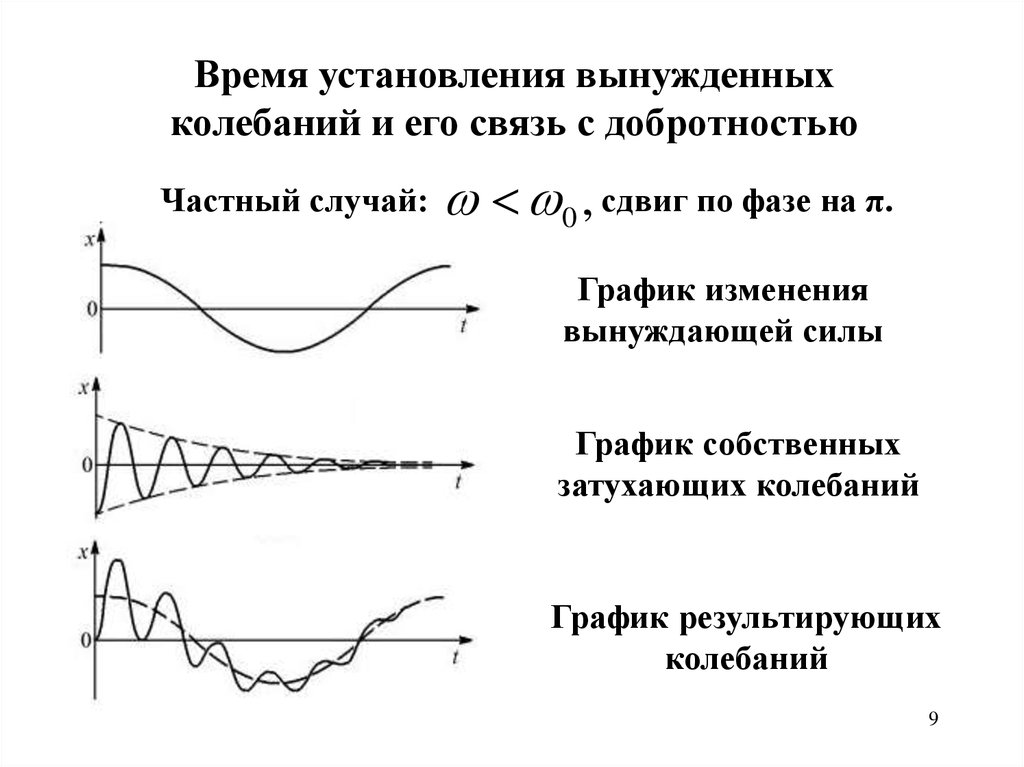
Время установления вынужденныхколебаний и его связь с добротностью
Частный случай:
0 , сдвиг по фазе на π.
График изменения
вынуждающей силы
График собственных
затухающих колебаний
График результирующих
колебаний
9
10.
Время установления вынужденныхколебаний и его связь с добротностью
Случай медленного затухания собственных колебаний:
• выше добротность,
• острее резонанс,
• больше запасаемая системой энергия.
Больше времени для сообщения энергии этой системе –
медленное установление колебаний.
Выше добротность - длительнее переходные процессы.
10
11.
Векторное представление колебательного движенияx A cos t
11
12.
Сложение колебаний одного направленияи одинаковой частоты
x1 A1 cos 0t 1
x2 A2 cos 0t 2
x x1 x2
A2 A12 A22 2 A1 A2 cos[ ( 2 1 )]
A12 A22 2 A1 A2 cos( 2 1 ),
A1 sin 1 A2 sin 2
tg
.
A1 cos 1 A2 cos 2
12
13.
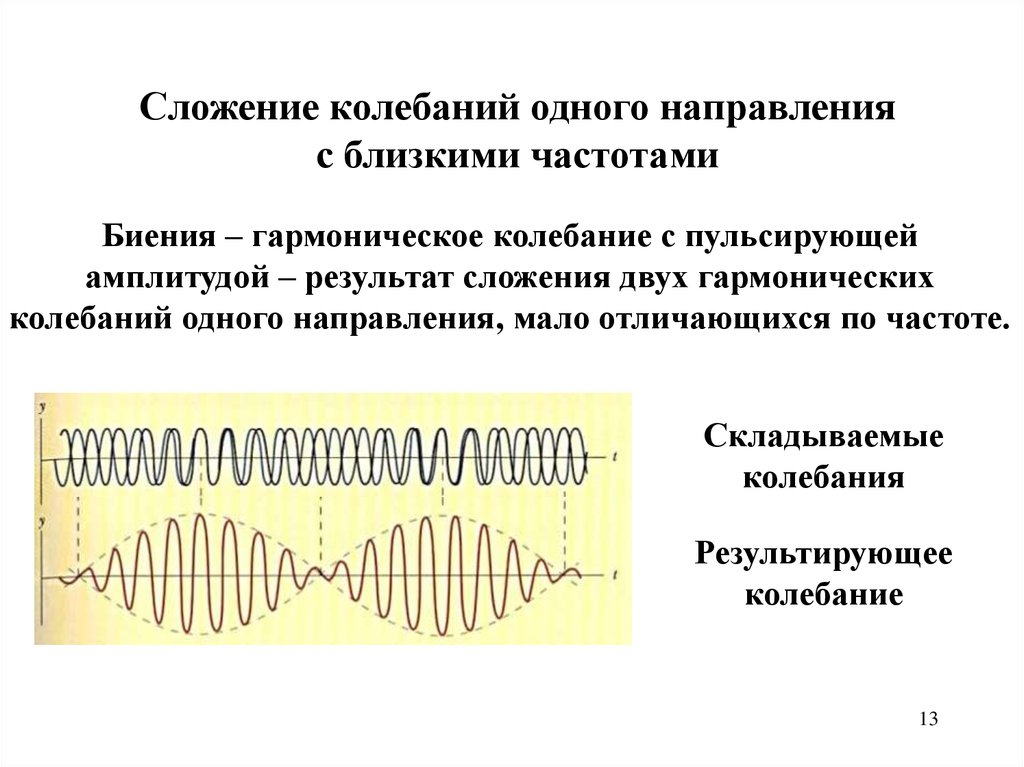
Сложение колебаний одного направленияс близкими частотами
Биения – гармоническое колебание с пульсирующей
амплитудой – результат сложения двух гармонических
колебаний одного направления, мало отличающихся по частоте.
Складываемые
колебания
Результирующее
колебание
13
14.
Сложение колебаний одного направленияс близкими частотами
x1 A cos t,
x2 A cos t
x x1 x2 2 A cos
t cos t
2
Медленно
изменяющаяся во
времени
амплитуда
-
частота биений (пульсаций амплитуды) равна
разности частот складываемых колебаний.
14
15.
Сложение взаимно перпендикулярных колебанийс одинаковыми частотами
x
cos t
x A cos t
A
2
x
y B cos( t )
sin t 1 2
A
y
cos t cos t cos sin sin t
B
x
x2
cos sin 1 2
A
A
2
2
2
x
y x
y x
x
2
cos sin 1 2
cos sin 1 2
B A
A
B A
A
x ex A cos t
y e y B cos( t )
x 2 y 2 2 xy
2
cos
sin
2
2
A B
AB
15
16.
x 2 y 2 2 xy2
cos
sin
.
2
2
A B
AB
Сложение взаимно перпендикулярных колебаний
с одинаковыми частотами
2
0:
x y
0.
A B
B
y x
A
- уравнение прямой.
16
17.
x 2 y 2 2 xy2
cos
sin
.
2
2
A B
AB
Сложение взаимно перпендикулярных колебаний
с одинаковыми частотами
2
:
B
x y
0. y x
A
A B
- уравнение прямой.
17
18.
x 2 y 2 2 xy2
sin
cos
2
2
AB
A B
Сложение взаимно перпендикулярных колебаний
с одинаковыми частотами
2
:
x2 y2
2 1
2
A B
- уравнение эллипса.
18
19.
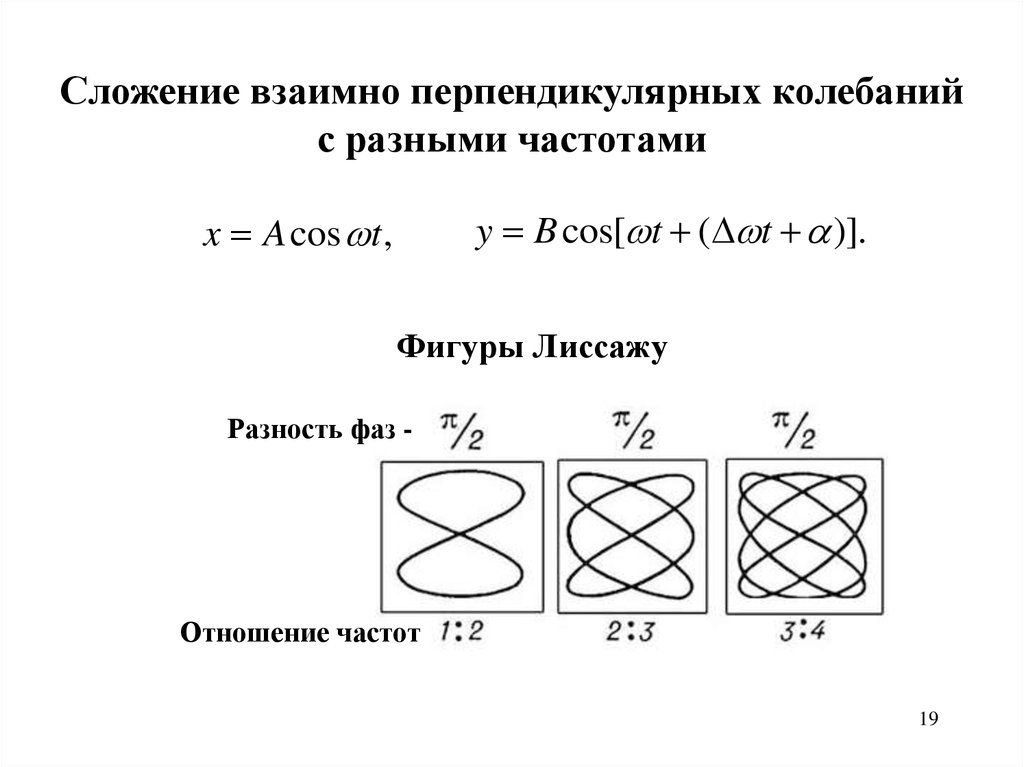
Сложение взаимно перпендикулярных колебанийс разными частотами
y B cos[ t ( t )].
x A cos t ,
Фигуры Лиссажу
Разность фаз -
Отношение частот
19
20.
Разложение и синтез колебанийФурье-анализ –
возможность представления периодических колебаний
комбинацией достаточного числа
гармонических (синусоидальных) колебаний.
Ряд Фурье y (t )
( A sin 2 f t B
n
n
n
cos 2 f nt ),
n
f n nf1 ,
An и Bn - амплитуды различных колебаний.
20
21.
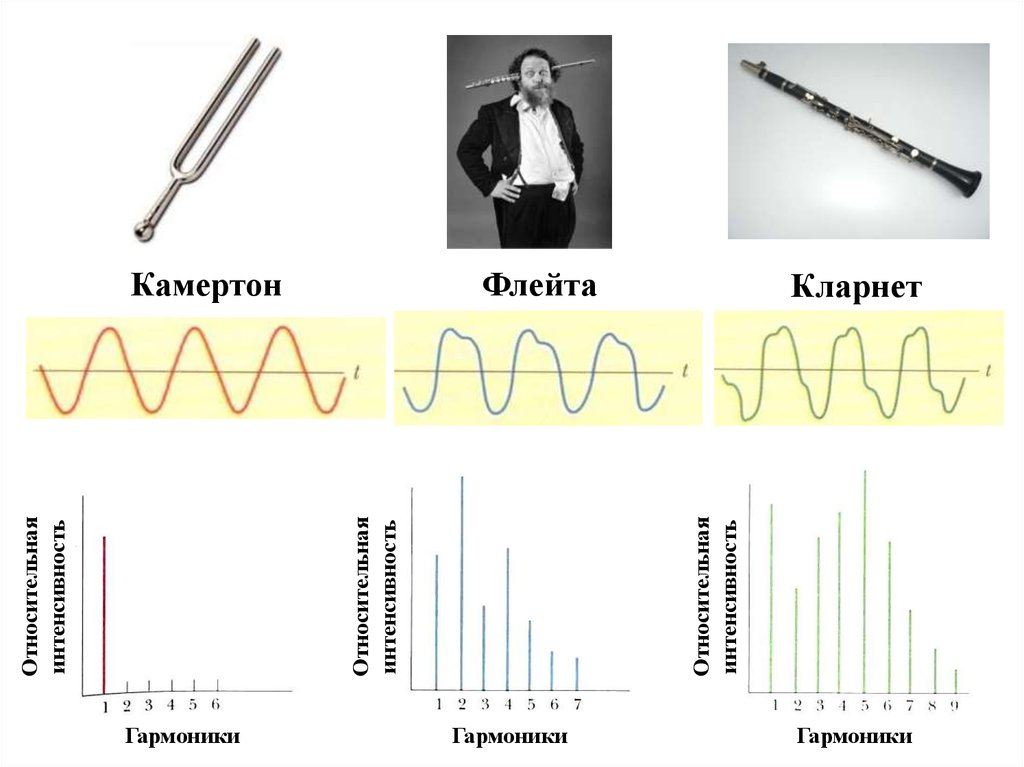
ГармоникиОтносительная
интенсивность
Относительная
интенсивность
Относительная
интенсивность
Камертон
Флейта
Гармоники
Кларнет
Гармоники
22.
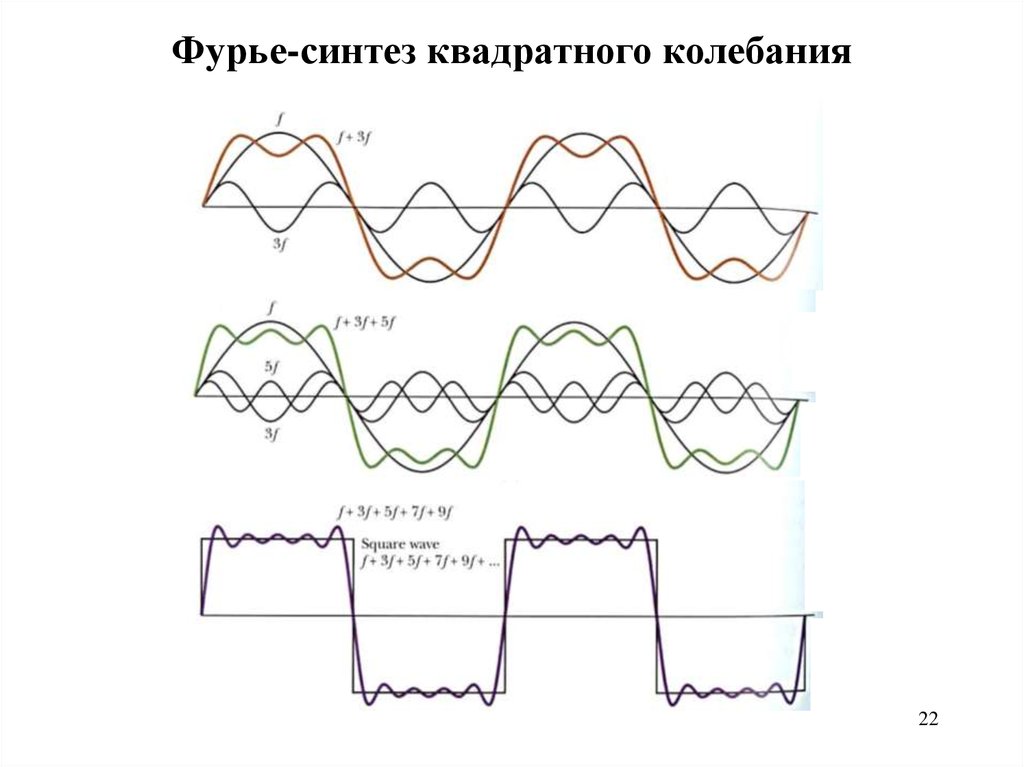
Фурье-синтез квадратного колебания22
23.
Передача сигналов на большие расстоянияТребование большой энергии сигналов.
Пропорциональность энергии сигнала
четвертой степени его частоты –
чем больше частота, тем больше энергия.
Практика: низкая частота колебаний у сигналов,
несущих в себе информацию, например, речевых сигналов.
Необходимость повышения частоты информационных
сигналов для их передачи на большие расстояния.
23
24.
Передача сигналов на большие расстоянияМодуляция –
накладывание низкочастотного информационного
сигнала на высокочастотный опорный сигнал.
24
25.
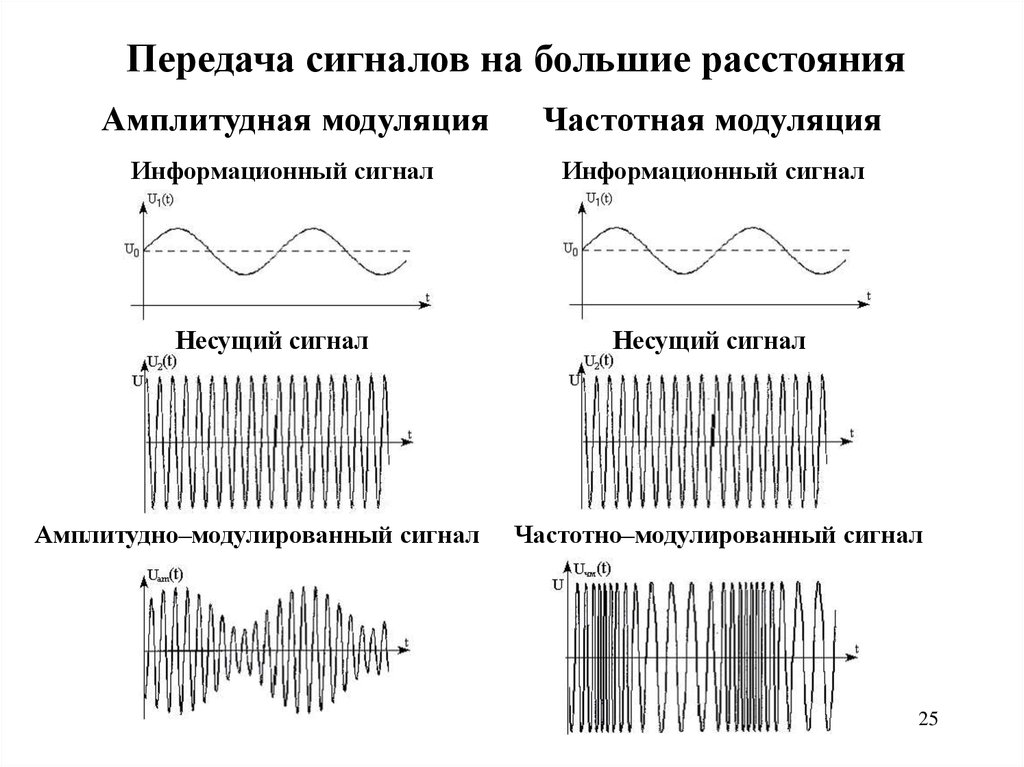
Передача сигналов на большие расстоянияАмплитудная модуляция
Информационный сигнал
Несущий сигнал
Амплитудно–модулированный сигнал
Частотная модуляция
Информационный сигнал
Несущий сигнал
Частотно–модулированный сигнал
25
26.
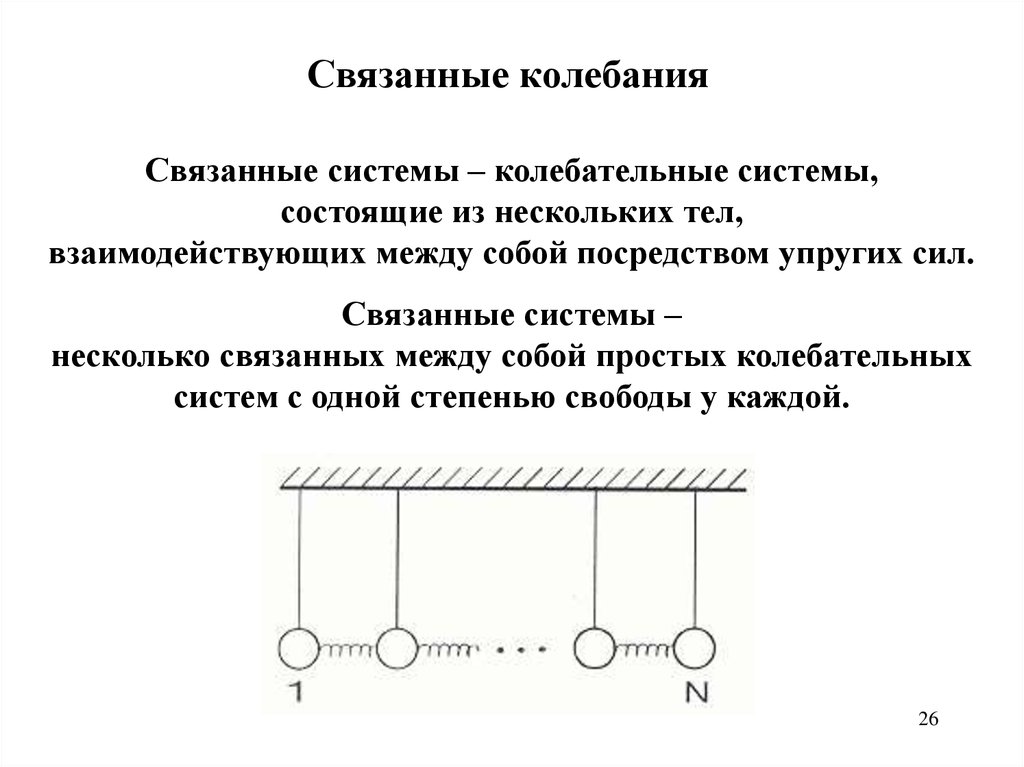
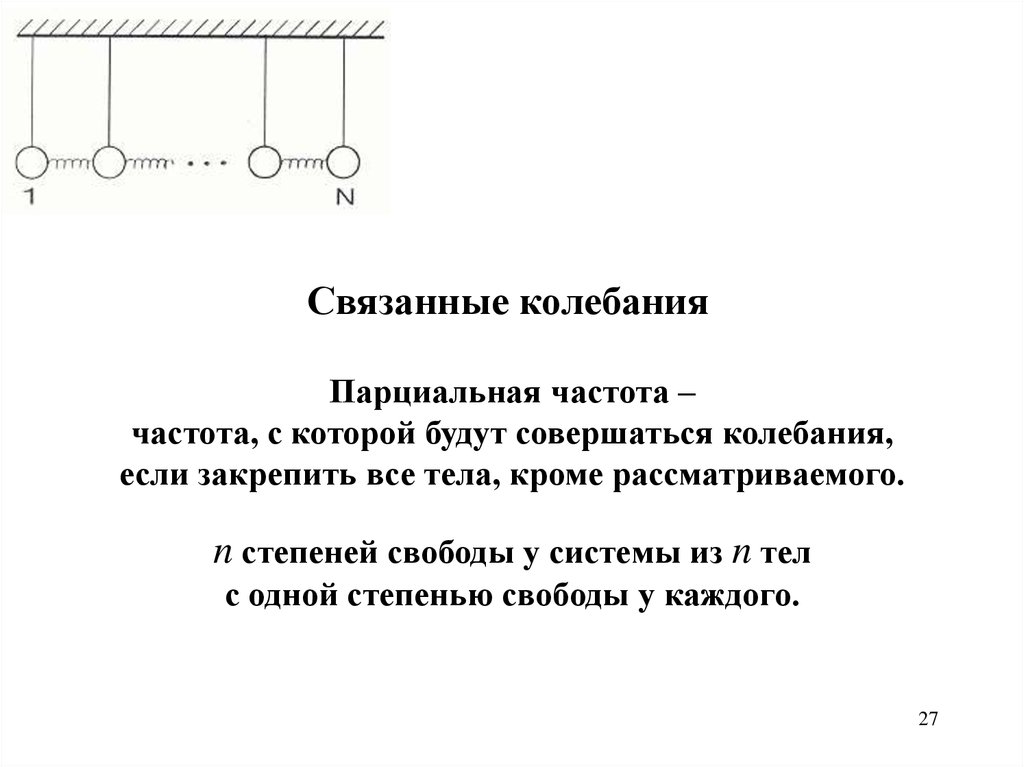
Связанные колебанияСвязанные системы – колебательные системы,
состоящие из нескольких тел,
взаимодействующих между собой посредством упругих сил.
Связанные системы –
несколько связанных между собой простых колебательных
систем с одной степенью свободы у каждой.
26
27.
Связанные колебанияПарциальная частота –
частота, с которой будут совершаться колебания,
если закрепить все тела, кроме рассматриваемого.
n степеней свободы у системы из n тел
с одной степенью свободы у каждого.
27
28.
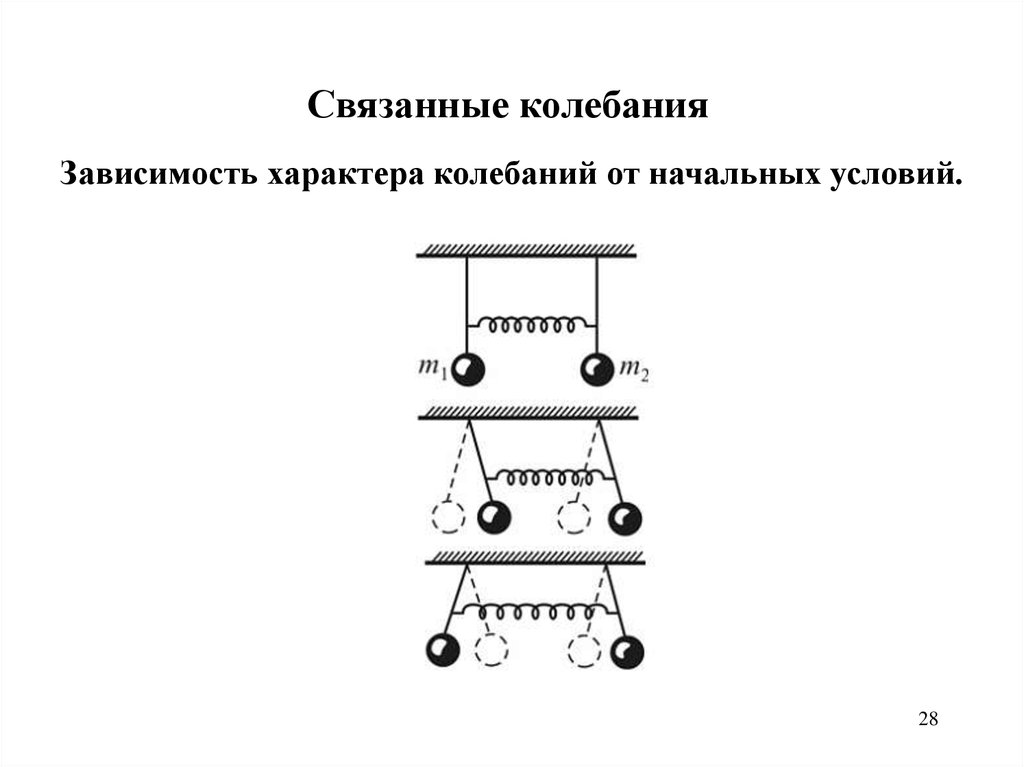
Связанные колебанияЗависимость характера колебаний от начальных условий.
28
29.
Связанные колебанияСмещение в одну сторону - синхронные колебания тел
с одинаковыми амплитудами, фазами и частотой 1,
равной частоте собственных колебаний.
1 – частота колебаний под действием силы тяжести
(пружина не оказывает влияния на колебания).
x1 A cos 1t
x2 A cos 1t
30.
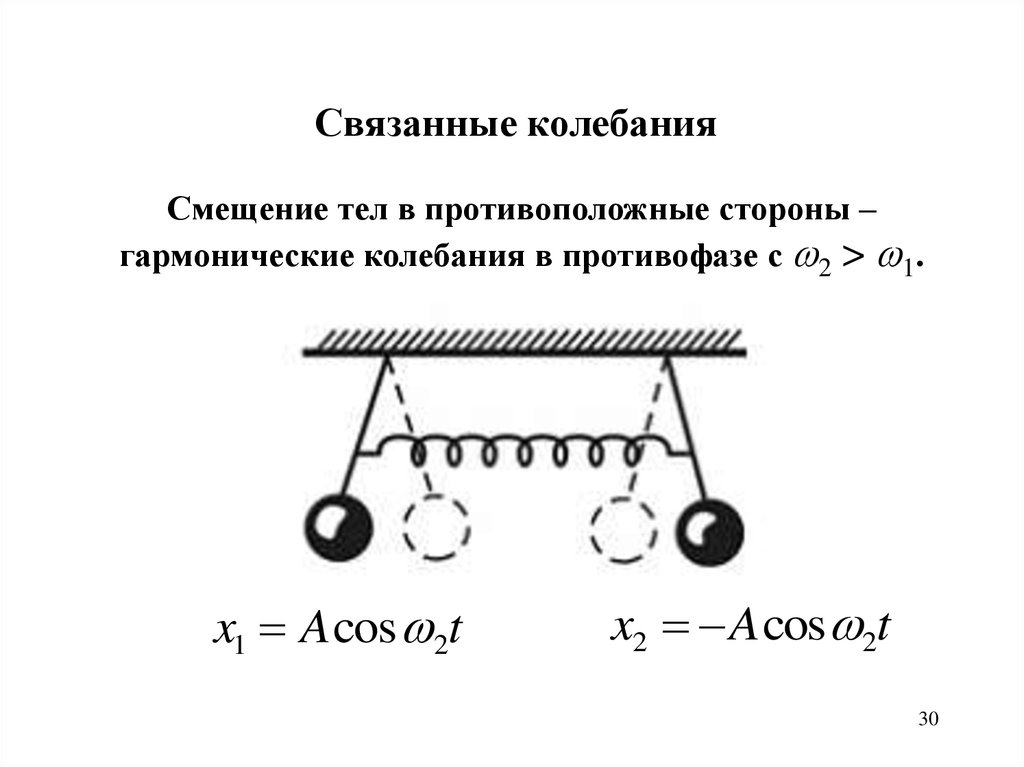
Связанные колебанияСмещение тел в противоположные стороны –
гармонические колебания в противофазе с 2 > 1.
x1 A cos 2t
x2 A cos 2t
30
31.
Связанные колебания1 и 2 – нормальные частоты колебаний тел системы,
а соответствующие колебания – нормальные колебания.
Соответствие числа степеней свободы системы
числу нормальных колебаний.
31
32.
Связанные колебанияДругие колебания системы –
суперпозиция нормальных колебаний.
Пример: суперпозиция нормальных колебаний
с одинаковыми амплитудами.
x1 A(cos 1t cos 2t ) 2 A cos
2 1
t cos t ,
2
2 1
x2 A(cos 1t cos 2t ) 2 A sin
t sin t ,
2
( 1 2 ) / 2.
Зависимость амплитуды колебаний от времени –
негармонические колебания.
32
33.
Связанные колебанияЖесткость пружины небольшая –
слабое воздействие на маятники:
2 1.
2 1
- возможность рассмотрения результирующих колебаний
как гармонических колебаний
с медленно меняющейся во времени амплитудой.
33
34.
x1 A(cos 1t cos 2t ) 2 A cos2 1
t cos t ,
2
2 1
x2 A(cos 1t cos 2t ) 2 A sin
t sin t.
2
Суперпозиция нормальных колебаний
с одинаковыми амплитудами
Начальные условия (t 0) :
x1 2 A,
Суперпозиция начальных
условий для нормальных
колебаний:
x2 0.
35.
Суперпозиция нормальных колебанийс одинаковыми амплитудами
x1
x2
Постепенный расход энергии,
сообщенной 1-ому маятнику при
его начальном отклонении,
на возбуждение колебаний 2-ого
маятника.
Концентрация энергии во 2-м
маятнике через промежуток
времени T0 /2 = / ( 2 - 1),
равный половине периода биений.
Далее: обратный переход энергии к 1-ому маятнику и
повторение связанных колебаний.
36.
T0 /2 = /( 2 - 1)Суперпозиция нормальных колебаний
с одинаковыми амплитудами
Равенство частоты биений (частоты передачи энергии)
разности нормальных частот колебаний системы.
Зависимость частоты биений в системе
от степени связи между колеблющимися телами.
Обусловленность процесса передачи энергии
между колеблющимися телами в системе
наличием связывающей их упругой пружины.
37.
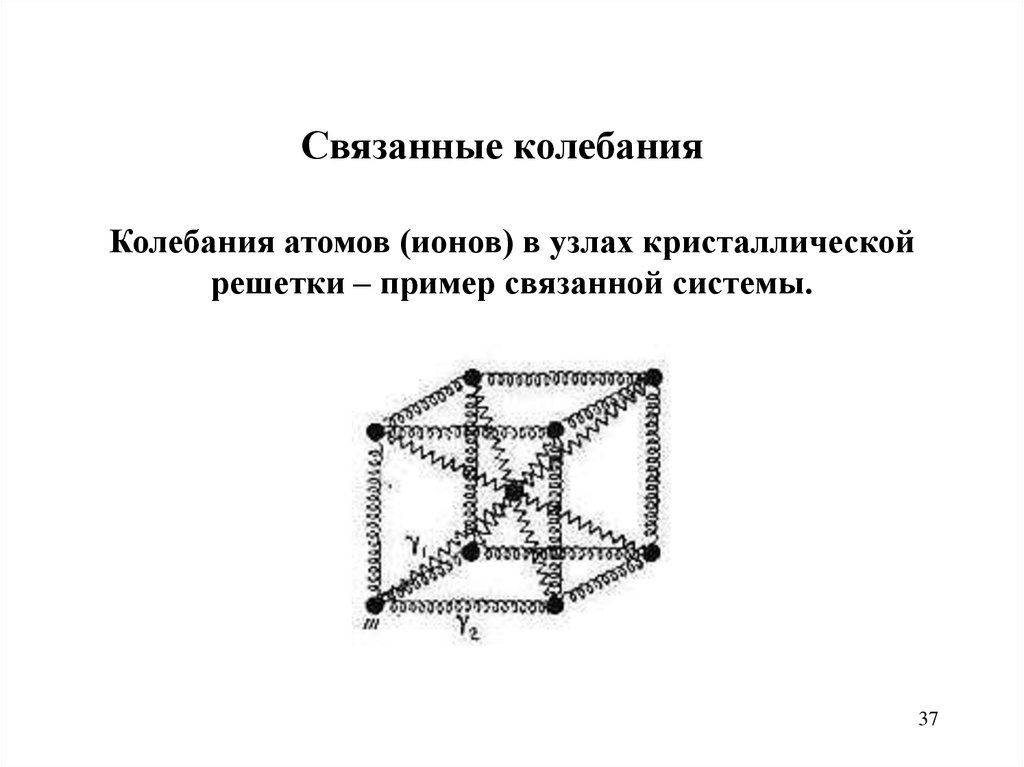
Связанные колебанияКолебания атомов (ионов) в узлах кристаллической
решетки – пример связанной системы.
37
38. Волновое движение
3839.
Волновое движениеВолновое движение - результат колебательного процесса.
39
40.
Волновое движениеДве разновидности волн –
механические и электромагнитные волны.
Распространение механических волн в какой-либо среде
(звуковые волны в воздухе, волны на поверхности воды,
упругие волны в твердом теле).
Распространение электромагнитных волн (видимый свет,
радиоволны, телевизионный сигнал, рентгеновские лучи)
даже в вакууме.
40
41.
Волновое движениеПредмет рассмотрения - механические волны.
Характеристики механических волн –
амплитуда, длина, частота,
направление и скорость распространения волны.
41
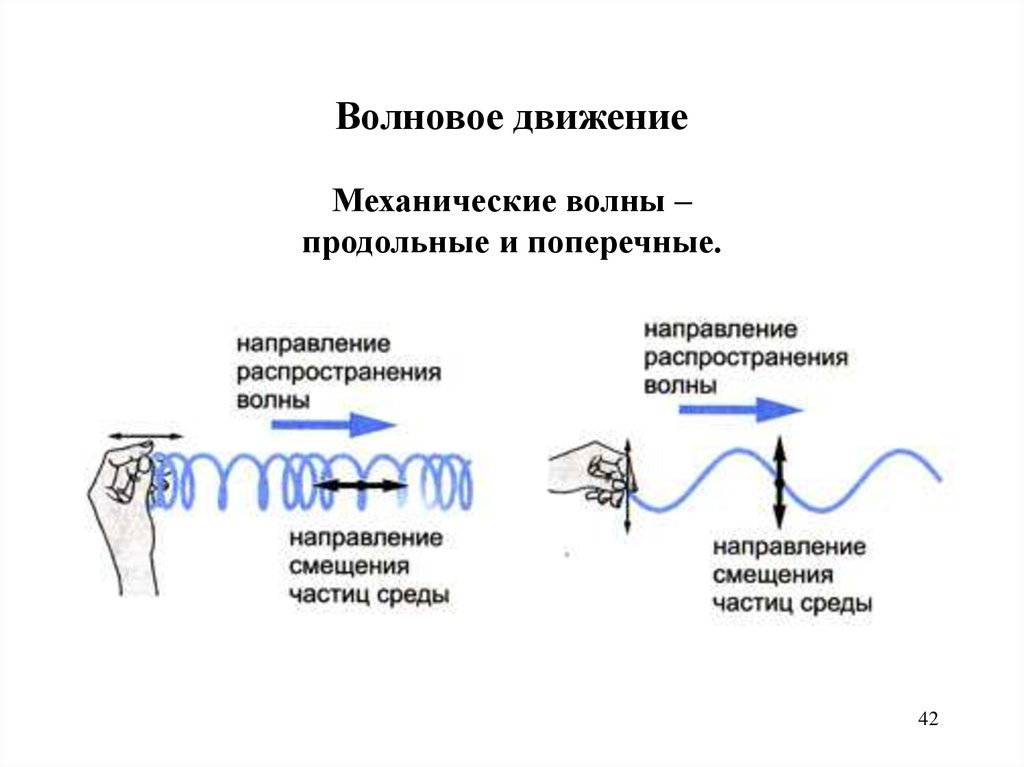
42.
Волновое движениеМеханические волны –
продольные и поперечные.
42
43.
Уравнение волны в газах, жидкостях и твердых телахПростейший случай – распространение синусоидальных волн.
Синусоидальные волны – результат гармонических колебаний.
Возможность описать распространение
продольной или поперечной волны
с использованием одинаковых аналитических выражений.
43
44.
Уравнение волны в газах, жидкостях и твердых телахПример: распространение поперечной волны в упругой среде.
y - положение точки упругой среды (смещение из
положения равновесия) в момент времени t.
y (x, 0) = f (x) – волновая функция,
описывающая профиль волны
(смещение точек упругой среды из положений равновесия)
в точке с координатой х в момент времени t = 0.
v – скорость распространения волны в упругой среде.
44
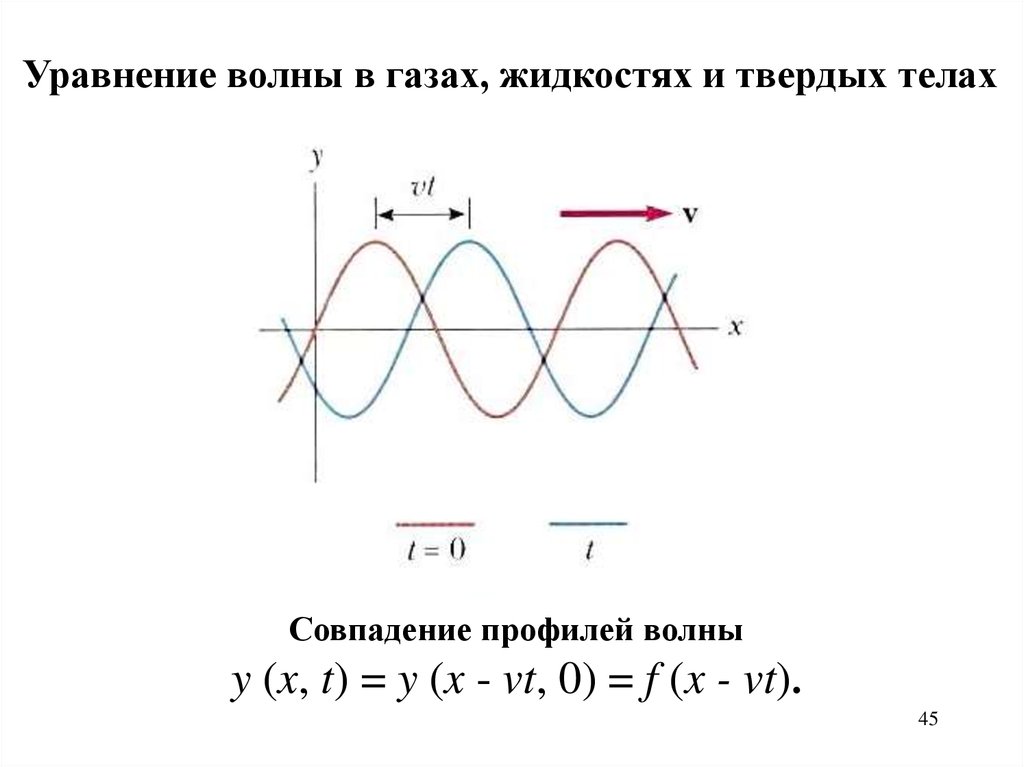
45.
Уравнение волны в газах, жидкостях и твердых телахСовпадение профилей волны
y (x, t) = y (x - vt, 0) = f (x - vt).
45
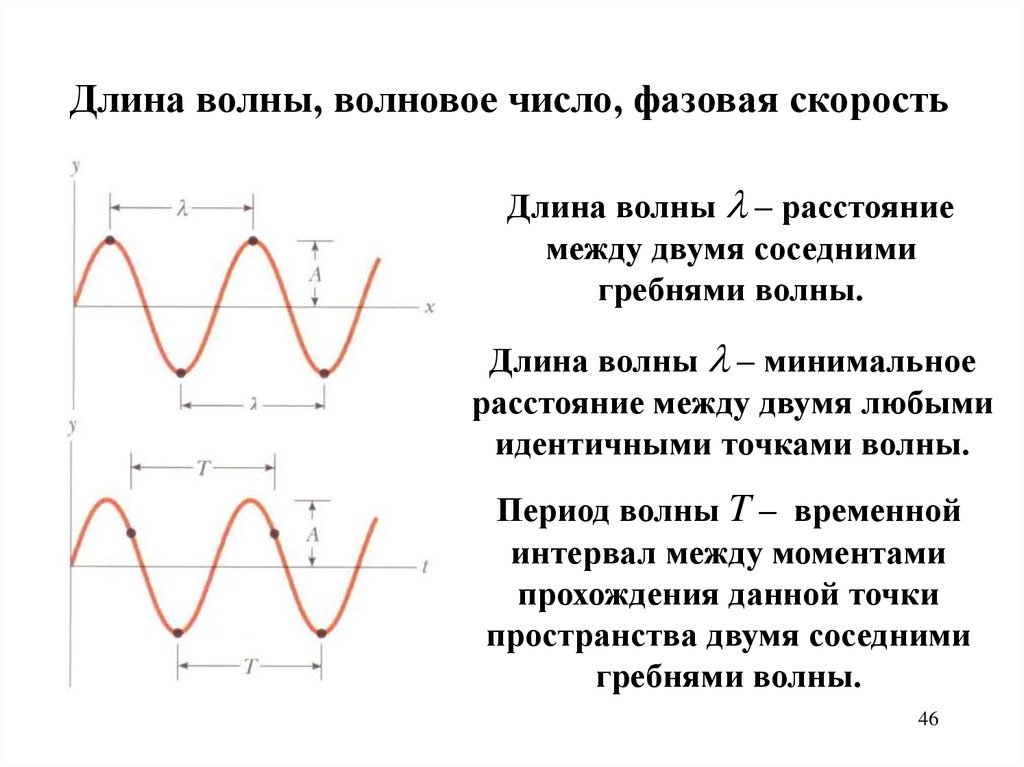
46.
Длина волны, волновое число, фазовая скоростьДлина волны – расстояние
между двумя соседними
гребнями волны.
Длина волны – минимальное
расстояние между двумя любыми
идентичными точками волны.
Период волны T – временной
интервал между моментами
прохождения данной точки
пространства двумя соседними
гребнями волны.
46
47.
Длина волны, волновое число, фазовая скоростьЧастота периодической волны f –
число гребней (или любых других идентичных точек) волны,
проходящих через данную точку пространства
за единичный интервал времени,
1
f .
T
Амплитуда А волны - максимальное смещение точки
среды из положения равновесия под воздействием волны.
47
48.
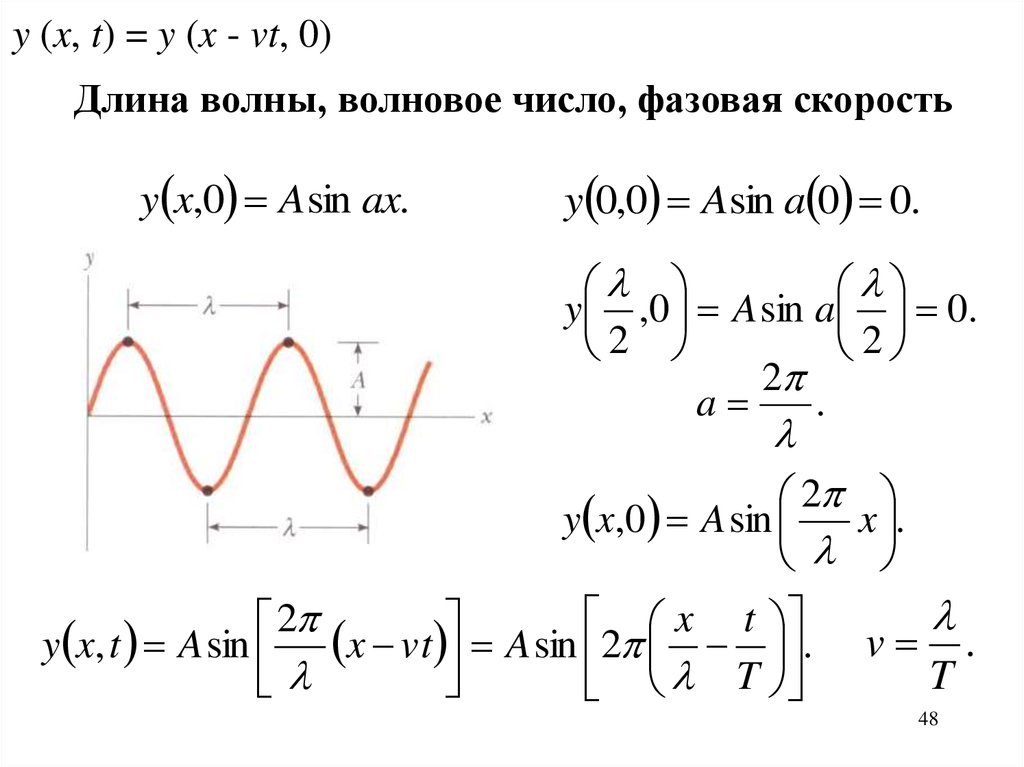
y (x, t) = y (x - vt, 0)Длина волны, волновое число, фазовая скорость
y x,0 A sin ax.
y 0,0 Asin a 0 0.
y ,0 A sin a 0.
2
2
2
a
.
2
y x,0 A sin
x t
2
y x, t A sin x vt A sin 2 .
T
x .
v
T
48
.
49.
x t2
y x, t A sin x vt A sin 2
T
Длина волны, волновое число, фазовая скорость
Волновое число
k
2
.
y A sin kx t .
Общий случай:
2
.
T
v
k
.
y Asin kx t .
Постоянная - фаза волны,
определяемая из начальных условий.
49
50.
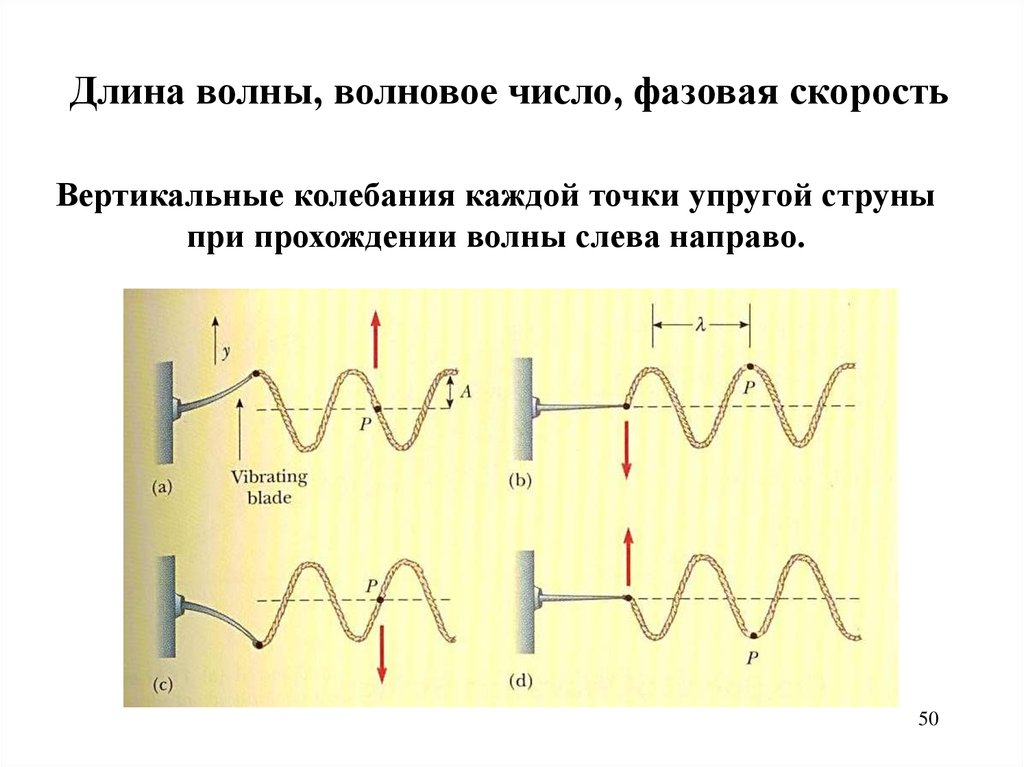
Длина волны, волновое число, фазовая скоростьВертикальные колебания каждой точки упругой струны
при прохождении волны слева направо.
50
51.
Длина волны, волновое число, фазовая скоростьУравнение волны
y A sin kx t
y
dy
vy
A cos kx t
dt x const t
v y
dv y
2
a y
A sin kx t
dt x const t
y 0:
v y ,max A.
y A:
a y ,max 2 A.
51
52.
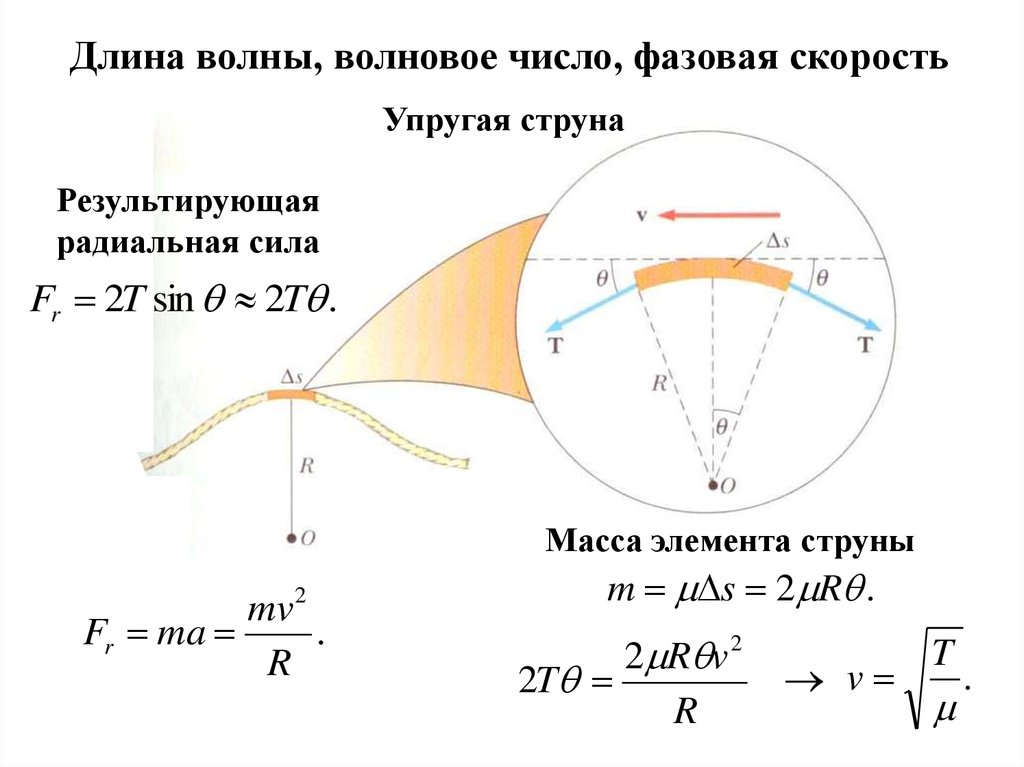
Длина волны, волновое число, фазовая скоростьУпругая струна
Результирующая
радиальная сила
Fr 2T sin 2T .
Масса элемента струны
mv2
Fr ma
.
R
m s 2 R .
2 R v 2
2T
R
v
T
.
53.
Одномерное волновое уравнениеВсе уравнения волны - решения волнового уравнения.
Элемент струны под действием растягивающих сил Т.
F
y
T sin B T sin A T sin B sin A .
F
y
T tan B tan A .
53
54.
Fy
T tan B tan A .
Одномерное волновое уравнение
2-й закон Ньютона:
y y
Fy T x x .
B
A
2 y
Fy may x t 2 .
y y
2 y
x 2 T .
t
x B x A
2 y
T t
2
y / x B y / x A
.
x
54
55.
2 yT t
2
y / x B y / x A
v
x
Одномерное волновое уравнение
f
f x x f x
lim
x x 0
x
2 y
2 y
2.
2
T t
x
2 y 1 2 y
2 2
2
x
v t
- общий вид одномерного волнового уравнения,
применимого для различных типов бегущих волн.
T
56.
Контрольный вопросСкорость поперечной волны в упругой среде
при увеличении амплитуды волны:
а) возрастает,
б) убывает,
в) не меняется,
г) нельзя однозначно ответить.
56






































 physics
physics








