Вынужденные колебания. Резонанс

1.

Кафедра физики
ЛЕКЦИЯ 9
ПЛАН ЛЕКЦИИ
1. Вынужденные колебания. Резонанс.
2. Колебательный контур. Свободные затухающие и
вынужденные электрические колебания в контуре.
Общая физика. «Физика колебаний и волн»

2.

Кафедра физики
Вынужденные колебания.
Интерес для техники представляет возможность поддерживать
колебания незатухающими.
Для этого необходимо восполнять потери реальной колебательной
системы с помощью периодически действующего фактора.
Пусть таким фактором в механической колебательной системе будет
действие вынуждающей силы, меняющейся по гармоническому закону:
F F0 cos t
где F0 и соответственно амплитуда и собственная частота
вынуждающей силы.
Рассмотрим пружинный маятник. Уравнение движения маятника:
d2x
m 2 kx
dt
Введем фактор диссипации энергии, например,
силу трения.
Общая физика. «Физика колебаний и волн»

3.

Кафедра физики
Вынужденные колебания.
Сила трения пропорциональна скорости:
dx
Fтр rv r
,
dt
где
r - коэффициент трения.
Закон движения маятника с учетом сил трения:
d2x
dx
m 2 kx r
dt
dt
Это уравнение свободных затухающих
колебаний пружинного маятника.
Пусть потери, возникающие в колебательной системе за счет действия
сил трения, компенсируются действием вынуждающей силы F .
Тогда уравнение движение маятника можно представить в виде:
d2x
dx
m 2 kx r
F0 cos t
dt
dt
Общая физика. «Физика колебаний и волн»

4.

Кафедра физики
Вынужденные колебания.
d2x
dx
m 2 kx r
F0 cos t
dt
dt
Преобразуем выражение. Разделим на m , введем обозначения:
ω0
r
k
- коэффициент затухания пружинного маятника.
,
m 2m
d2x
dx F0
2
Итог:
x
2
cos t , или
0
2
dt
dt m
F0
d2x
dx
2
2
x
cos t
0
2
dt
dt
m
Это линейное неоднородное дифференциальное
вынужденных колебаний пружинного маятника.
Общая физика. «Физика колебаний и волн»
уравнение

5.

Кафедра физики
Вынужденные колебания.
x
F0
d2x
dx
2
2
0 x cos t
2
dt
dt
m
t
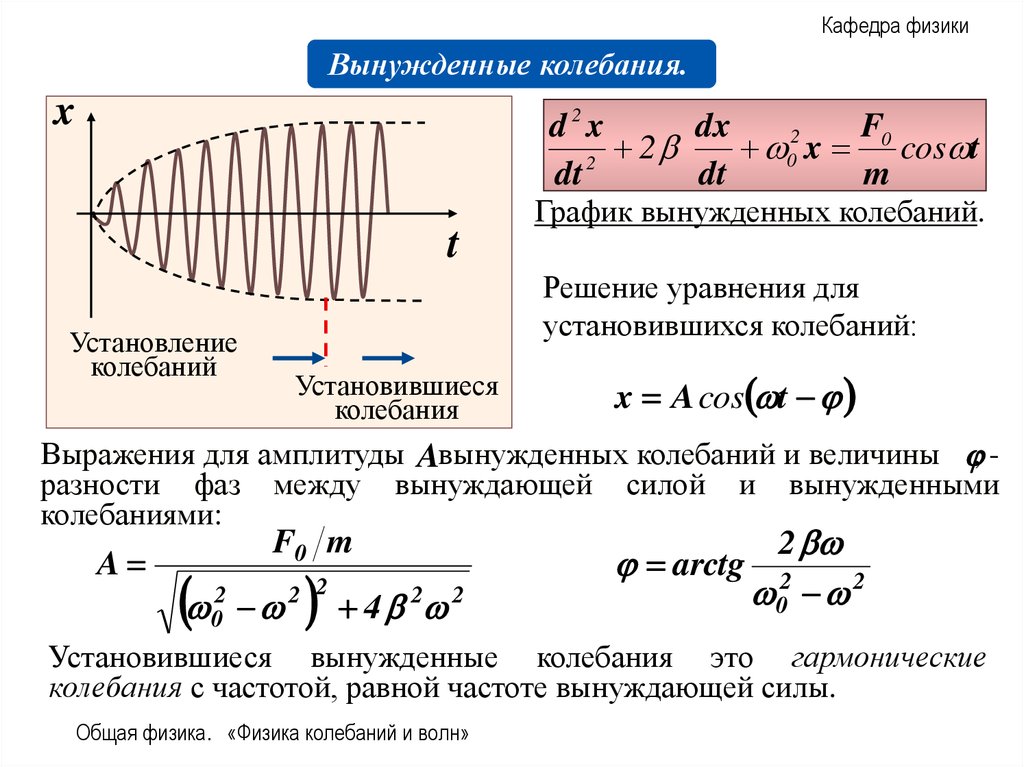
График вынужденных колебаний.
Решение уравнения для
установившихся колебаний:
Установление
колебаний
Установившиеся
колебания
x A cos t
Выражения для амплитуды Aвынужденных колебаний и величины , разности фаз между вынуждающей силой и вынужденными
колебаниями:
A
02
F0 m
2 2
4 2 2
2
arctg 2
0 2
Установившиеся вынужденные колебания это гармонические
колебания с частотой, равной частоте вынуждающей силы.
Общая физика. «Физика колебаний и волн»

6.

Кафедра физики
Вынужденные колебания.
Амплитуда вынужденных колебаний зависит от частоты
вынуждающей силы. Это приводит к тому, что при некоторой
определенной для системы частоте амплитуда колебаний достигает
максимального значения.
Это явление – резонанс. Частота – резонансная частота.
Для определения резонансной частоты нужно найти минимум
выражения, стоящего в знаменателе соотношения для амплитуды
вынужденных колебаний.
2
2 2
2 2
F
m
Если продифференцировать знаменатель
4
0
0
A
2
2 2
и приравнять его к нулю,
получим
для резонансной
0 4 выражение
2 2
частоты в виде:
рез 02 2 2
Общая физика. «Физика колебаний и волн»

7.

Кафедра физики
Вынужденные колебания.
Выражение для амплитуды при резонансе:
A
F0 m
2 02 2
При отсутствии сопротивления среды ( 0 ) амплитуда при резонансе
обращается в бесконечность.
Польза: акустика, радиотехника.
Вред: опасные вибрации корпуса корабля или крыльев самолета
при совпадении собственной частоты колебаний с частотой
колебаний, возбуждаемых вращением гребного винта или
пропеллера.
Общая физика. «Физика колебаний и волн»

8.

Кафедра физики
Электромагнитные колебания.
Колебательный контур.
Колебательный контур – это электромагнитная система, в которой
электрические величины (токи, заряды) периодически изменяются.
R
L
C
Состав:
последовательно
включенные
резистор сопротивлением R , катушка
индуктивностью L , и с конденсатор
емкостью C .
Идеализированный контур, это контур, сопротивление которого
пренебрежимо мало ( R 0 ).
Общая физика. «Физика колебаний и волн»

9.

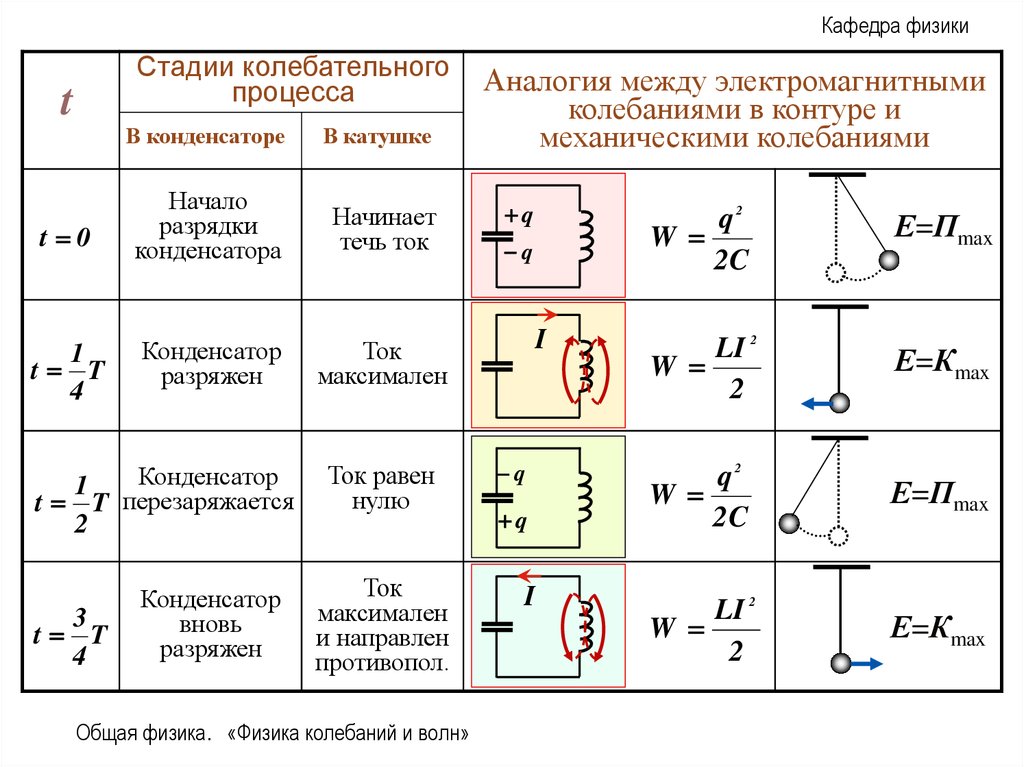
Кафедра физики
Стадии колебательного
процесса
t
В конденсаторе
В катушке
t 0
Начало
разрядки
конденсатора
Начинает
течь ток
1
t T
4
Конденсатор
разряжен
Ток
максимален
Конденсатор
1
t T перезаряжается
2
3
t T
4
Конденсатор
вновь
разряжен
Ток равен
нулю
Ток
максимален
и направлен
противопол.
Общая физика. «Физика колебаний и волн»
Аналогия между электромагнитными
колебаниями в контуре и
механическими колебаниями
q
q
I
q
q
I
q2
W
2C
Е=Пmax
LI 2
W
2
Е=Кmax
q2
W
2C
Е=Пmax
LI 2
W
2
Е=Кmax

10.

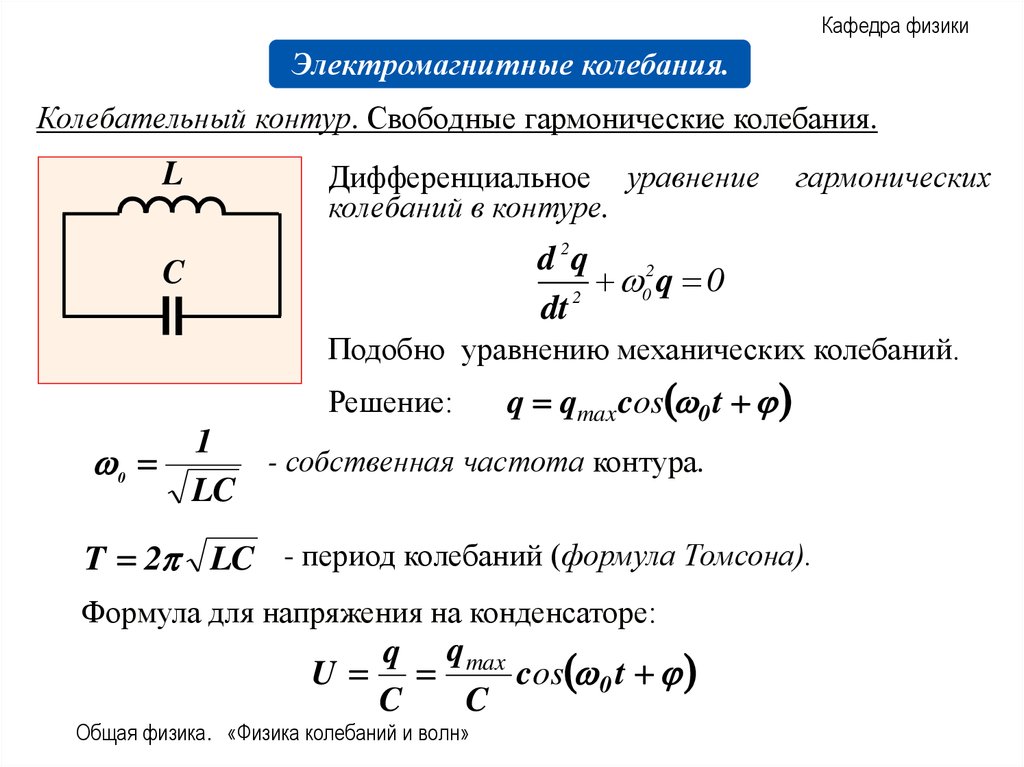
Кафедра физики
Электромагнитные колебания.
Колебательный контур. Свободные гармонические колебания.
L
Дифференциальное уравнение
колебаний в контуре.
гармонических
d 2q
2
q 0
0
2
dt
C
Подобно уравнению механических колебаний.
Решение:
0
q qmax cos 0 t
1
- собственная частота контура.
LC
T 2 LC - период колебаний (формула Томсона).
Формула для напряжения на конденсаторе:
q q max
U
cos 0 t
C
C
Общая физика. «Физика колебаний и волн»

11.

Кафедра физики
Электромагнитные колебания.
Колебательный контур. Свободные гармонические колебания.
L
Продифференцировав соотношение для
заряда, получим выражение для тока в
контуре :
3
I
C
q
2
q
d q
2
q 0
0
2
dt
q qmax cos 0 t
qmax
U
cos 0 t
C
I qmax 0 sin 0 t
dq
Видно, что сила тока опережает по фазе
I
напряжение
на конденсаторе на 2.
dt
I I max cos 0 t
2
В момент, когда ток достигает наибольшего
значения, заряд и напряжение обращаются
в нуль и наоборот.
Общая физика. «Физика колебаний и волн»

12.

Кафедра физики
Электромагнитные колебания.
Свободные затухающие колебания в контуре.
Реальный контур обладает активным сопротивлением.
Энергия, запасенная в контуре, постепенно расходуется на этом
сопротивлении на нагревание, свободные колебания затухают.
Дифференциальное уравнение затухающих колебаний в контуре:
d 2q
dq
2
2
q 0
0
2
dt
dt
Подобно уравнению механических колебаний.
R
2L
Общая физика. «Физика колебаний и волн»
0
1
LC

13.

Кафедра физики
Электромагнитные колебания.
Свободные затухающие колебания в контуре.
2
R
1
При условии, что 2 0 , т.е. при
решение уравнения
2
4L
LC
затухающих колебаний имеет вид
2
q qmax 0 e t cos t
где 02 2 .
Если в это выражение подставить соответствующие выражения для
и 0 , получим следующее соотношение для частоты затухающих
колебаний:
2
При R 1
получится выражение для
0 R
частоты
собственной
незатухающих
2
LC
4
L
свободных колебаний в контуре.
Общая физика. «Физика колебаний и волн»

14.

Кафедра физики
Электромагнитные колебания.
Вынужденные колебания в контуре.
Для компенсации потерь в колебательном контуре нужно оказывать
на контур периодически изменяющееся воздействие.
Это можно осуществить, например, включив последовательно с
элементами контура переменное напряжение.
R
L
U U max cos t
C
Уравнение вынужденных колебаний:
U max
d 2q
dq
2
2
0 q
cos t
2
dt
dt
L
U
Решение для установившихся колебаний:
qmax
ω
U max L
2
0
ω
2
2
4β 2 ω 2
Общая физика. «Физика колебаний и волн»
q qmax cos t
arctg
2
02 2