Similar presentations:
Колебательный контур. Свободные и вынужденные колебания. Резонанс
1.
2.
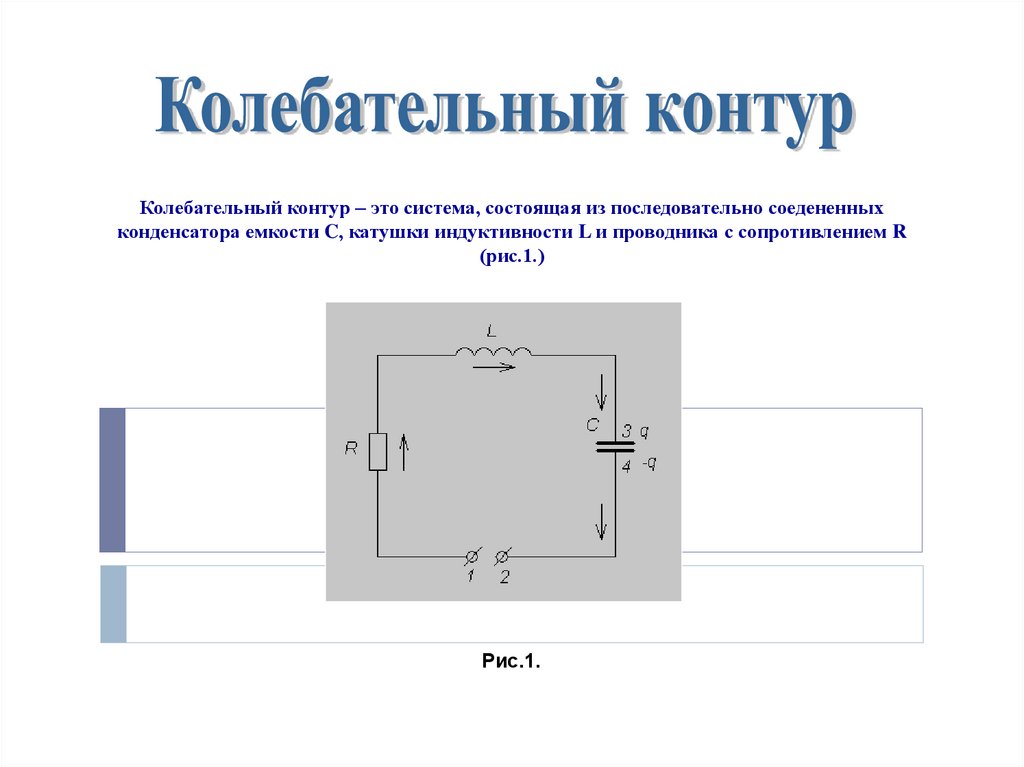
Колебательный контур – это система, состоящая из последовательно соедененныхконденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R
(рис.1.)
Рис.1.
3.
U R RIdI
UL L
dt
q
UC
C
U R U L UC
4.
Если нет сопротивления, то электрические колебания в колебательном контуре будутнезатухающими
qm2
a) Wp
2C
LI m2
б ) Wм
2
qm2
в ) Wp
2C
LI m2
г ) Wм
2
qm2
д) W p
2C
5.
qm2 CU m2We
максимальная энергия электрического поля
2C
2
LI m2
Wm
максимальная энергия магнитного поля
2
Полная энергия
Li 2 q 2 LI m2 qm2
W
2 2C
2
2C
Где i и q – сила тока и электрический заряд в любой момент времени
6.
Свободные электромагнитные колебания – это периодическиповторяющиеся изменения электромагнитных величин (q –
электрический заряд, I – сила тока, U – разность потенциалов),
происходящие без потребления энергии от внешних источников.
7.
d 2qdq q
L 2 R уравнение колебательного контура
dt
dt C
02
1
LC
R
2
L
X
C
q 2 q 02 q x
где 0 собственная частота колебаний системы
коэффициен тзатухания
Если сопротивление R равно нулю:
q 02 q 0 свободные незатухающие колебания
Решение этого уравнения:
q q0 cos( 0t )
8.
Если какая-либо величина меняется по времени по закону q q0 cos( 0t )то она совершает гармонические колебания.
Промежуток времени, через который значения колеблющихся величин
периодически повторяются, называется периодом колебания:
T0
2
0
Число колебаний в единицу времени называется частотой колебаний:
q0 амплитуда колебания
1 0
0
T 2
Для электрических колебаний собственная
1
0t фаза колебания
частота : 02
LC
начальная фаза колебания
T0 2 LC
- Формула Томпсона
9.
Свободные электромагнитные колебания в реальном колебательном контуре, представляющем собойпоследовательное соединение катушки индуктивности L, конденсатора емкости С и электрического
сопротивления R – называются затухающими электромагнитными колебаниями
Уравнение изменения заряда q на обкладках конденсатора во времени:
t
Решение уравнения:
0
з
q q e
sin( t )
L q R q
q
0
C
q0 амплитудное значение заряда в момент времени t 0
R
коэффициент затухания
2L
Циклическая частота свободных
электромагнитных колебаний в контуре:
з
1
R2
LC 4 L2
Период затухающих колебаний:
T
2
з
2
1
R2
LC 4 L2
Зависимость заряда от времени при затухающем колебании
10.
Незатухающие колебания в цепи под действием внешней, периодически изменяющейсяЭДС – называются вынужденными электромагнитными колебаниями
e Em sin t
e мгновенное значение ЭДС индукции (в данный момент времени )
Em амплитудное значение ЭДС
циклическая частота переменной ЭДС
Магнитный поток Ф сквозь плоскость рамки:
BS cos
угол между нормалью n к плоскости рамки и напряжением
вектора магнитной индукции B
По закону электромагнитной индукции:
скоростьизменения магнитной индукции
t
E
t
e BS sin t Em sin t
Em BS амплитуда ЭДС индукции
11.
Z R2 X 2где X X L X C
реактивное сопротивление колебательного контура
Z R 2 ( L
1 2
)
C
Из закона Ома для участка цепи переменного тока:
U
I
R 2 ( L
1 2
)
C
Сдвиг фаз между колебаниями силы тока и напряжения (отношение реактивного
сопротивления к активному):
tg
X
R
L
R
1
C
12.
Явление резкого возрастания амплитуды вынужденных колебаний тока в колебательном контуре, котороепроисходит при совпадении частоты вынужденных колебаний с собственной частотой колебательного
контура – называется резонансом.
Im
Если Um = const , то амплитуда вынужденных колебаний
силы тока зависит от ω :
R не зависит от L
0 собственная частота колебаний
1
справедливо, если
C
Um
Z
Um
R 2 ( L
1 2
)
C
1
0
LC
резонансная частота (частота переменного тока, прикоторой сила тока максимальна)
U mC U mL I m L
Im
Im
U резонансное напряжение
C
Um
1
U m C
I mC I mL
X
L
Если 0
I mC и I mL амплитудные значения силы токов
U m амплитудное значение приложенного U
1
I mC I mL , I m 0, R
LC
Условие резонанса токов:
0
1
LC











 physics
physics








