Similar presentations:
Колебания. Свободные и вынужденные колебания. Математический маятник
1.
КолебанияКолебаниями называются движения или процессы,
обладающие определенной повторяемостью во времени.
Гармоническими называются колебания, которые
происходят по закону синуса (косинуса).
Гармонические колебания величины Ψ описываются
уравнением типа
Ψ (t) = Acos( t+ 0).
Гармонические колебания происходят под действием
упругой или квазиупругой силы. Это силы
пропорциональные смещению и направленные к
положению равновесия, то есть подчиняющиеся закону
Гука:
F(x) = - kx,
где k – коэффициент упругости.
2.
По характеру внешних воздействий колебаниябывают свободные и вынужденные.
Свободными называются колебания, возникающие в
системе, которая в результате кратковременного
воздействия выведена из положения равновесия и затем
предоставлена самой себе.
• Если колебания такой системы происходят только под
действием внутренних сил, которые, как правило,
являются упругими или квазиупругими, то такие
колебания называются собственными. В реальных
условиях
свободные
колебания
являются
затухающими, так как они происходят при наличии
различного вида сил сопротивления.
• Вынужденными называются колебания, происходящие
под действием внешней периодической вынуждающей
силы.
3.
Параметры гармонических колебанийΨ (t) = Acos( 0t+ 0)
Ψ – обобщённый параметр, изменяющийся по
гармоническому закону;
А – амплитуда колебаний, наибольшее отклонение
параметра Ψ от равновесного значения;
( 0t+ 0) – фаза колебаний;
0 – начальная фаза;
0-собственная циклическая частота колебаний, число
колебаний за время 2 π секунд;
- линейная частота колебаний, число колебаний в
единицу времени;
0 = 2 , ωο = dφ/dt
Т - период колебаний, время одного полного колебания;
Т = 1/ = 2 / 0
4.
Кинематика гармонических колебаний• Ψ (t) = Acos( 0t+ 0)
• Скорость колеблющейся частицы
= -A 0sin( 0t+ 0) = A 0 cos( 0t+ 0+ /2)
υ=
• Ускорение колеблющейся частицы
= -A 02cos( 0t+ 0) = A 02 cos( 0t+ 0+ )
a=
а = - 02Ψ
Дифференциальное уравнение
гармонических колебаний
Дифференциальное уравнение гармонических колебаний
имеет вид: а+ω 2Ψ=0 или:
2 0
0
его решение Ψ = Acos( 0t+ 0)
0
5.
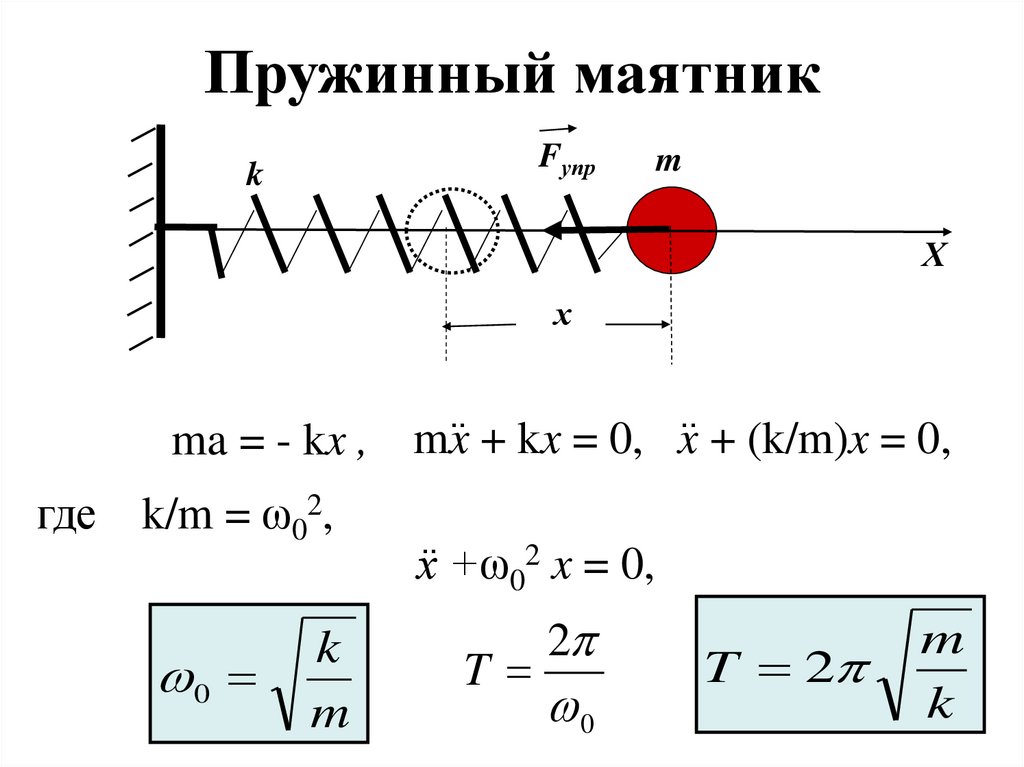
Пружинный маятникFупр
k
m
Х
х
ma = - kx , mx˙˙ + kx = 0, x˙˙ + (k/m)x = 0,
где k/m = ω02,
0
k
m
х˙˙ +ω02 x = 0,
T
2
0
T 2
m
k
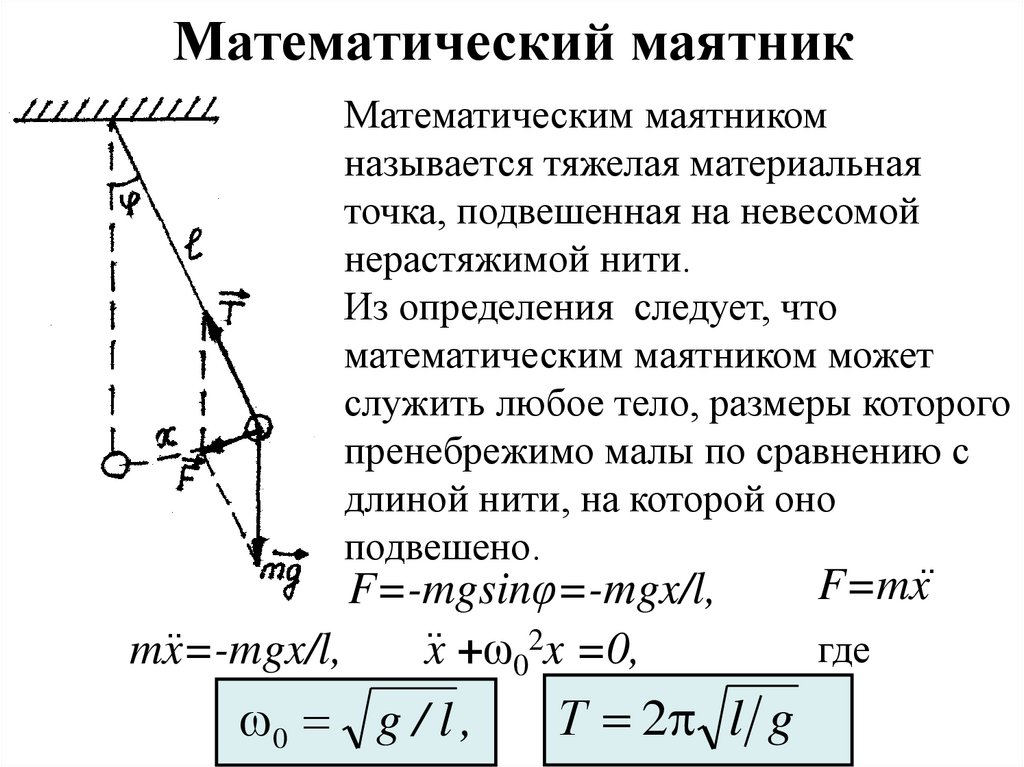
6. Математический маятник
хg
x 0,
l
Математическим маятником
называется тяжелая материальная
точка, подвешенная на невесомой
нерастяжимой нити.
Из определения следует, что
математическим маятником может
служить любое тело, размеры которого
пренебрежимо малы по сравнению с
длиной нити, на которой оно
подвешено.
F=-mgsinφ=-тgx/l,
˙˙
mx=-mgx/l,
x˙˙ +ω02x =0,
0 g / l ,
Т 2 l g
F=mẋ˙
где
7. Физический маятник
рℓпр
α ℓ
С
.
Физическим маятником называют
твердое тело, совершающее
колебания под действием силы
тяжести относительно оси, не
проходящей через центр тяжести
тела.
М ( ) mg sin ,
, J mg sin
М ( ) J
mg
2
0,
0 0;
J
mg
J
, T 2 2 J
пр
J
0
mg
m
mg
0
T 2
пр
g
8. Колебательный контур
• Колебательный контур – цепь, состоящая извключенных последовательно катушки индуктивностью
L, конденсатора емкостью С и резистора
сопротивлением R.
9. Гармонические колебания в колебательном контуре
Если R=0, то потерь энергии в контуре небудет, и колебания будут носить
периодический незатухающий характер, т.е.
заряд q на обкладках конденсатора,
напряжение U на конденсаторе и сила тока I,
текущего через катушку индуктивности, будут
меняться по гармоническому закону.
dI
q
IR + Uc = εs. При R=0 IR = 0. U c ,
S L
dt
C
dI q
1
2
L 0;
q
q 0,
q
q
0
0
dt C
LC
1
0
LC
Т 2 LC
10. Электромеханическая аналогия
• х ↔ q• υ ↔ I
• k ↔ (1/С)
•m ↔ L
• Wкин ↔ Wмагн
• Wпот ↔ Wэл
11.
Затухающие колебания1. Пружинный
маятник
Fтр r rx
• В вязкой среде
r – коэффициент
сопротивления.
m x kx rx
ma Fу Fтр ;
r
k
x
x
x 0;
Обозначим:
m
m
2
k / m 0
r / m 2 ,
х
х
x 2 x 02 x 0
Fтр
Решение уравнения:
х = х0 е-βt соs(ωt + φ0)
А = х0 е-βt - амплитуда затухающих колебаний;
ω=
Т=
02 2
2
02 2
- частота затухающих колебаний;
- период затухающих колебаний.
12.
Амплитуда затухающих колебаний:
А = х0 е-βt
Логарифмический декремент затухания:
θ = ln(An /An+1)
θ = βΤ
Время релаксации τ –время за которое амплитуда
колебаний уменьшается в е раз:
A( t )
e,
A( t )
t
x0 e
e e,
( t )
x0 e
β = 1/τ = 1/(Ne Τ) ,
θ = βΤ = 1/Ne ,
βτ=1
θ = 1/Ne
13.
2. Колебательный контур• Дифференциальное уравнение свободных затухающих
колебаний заряда в контуре (при R 0) имеет вид:
dI
q
L
IR
0;
dt
C
• Его можно переписать в виде:
d 2 q R dq 1 q 0
dt 2 L dt LC
R
2
• Вводя обозначения
L
• получим
и
1
2 ,
0
LC
d 2 q 2 dq 2q 0
0
dt
dt 2
q q0e t cos( t 0 )
• Решение уравнения имеет вид:
где
о2
2
2
1
R
LC 4 L2
14.
Вынужденные электромагнитные колебания.Закон Ома для переменного тока.
• Переменный ток можно рассматривать как
установившиеся вынужденные электромагнитные
колебания в цепи, содержащей резистор, катушку
индуктивности, конденсатор и источник
вынуждающей ЭДС.
• Мы будем рассматривать квазистационарные токи,
для которых мгновенные значения силы тока во всех
сечениях цепи практически одинаковы.
• Для мгновенных значений квазистационарных токов
выполняются закон Ома и вытекающие из него
правила Кирхгофа.
15.
СR
ε
~
UR+Uc = εi+ε
L IR+q/C= -L(dI/dt)+ε cosωt
0
R
1
I I
I 0 sin t
L
LC
L
Рисунок 1
где
I 2 I 02 I e0 sin t
Решение уравнения:
I0
0
I=I0 cos(ωt-φο)
(1)
2
2
L
1
/(
C
)
R
- закон Ома для
переменного тока
Разность фаз между напряжением и силой тока:
L 1 /( С )
tg 0
R
16.
Z2
2
L
1
/(
C
)
R
2
2
R (R L R C )
называется полным сопротивлением цепи
RL = ωL - индуктивное сопротивление;
RC = 1/ (ωC) - ёмкостное сопротивление;
1 - реактивное
X RL RC L
C сопротивление.
Реактивное сопротивление не вызывает тепловых
потерь в цепи переменного тока. Оно создаёт сдвиг
фаз между током и вынуждающей э.д.с.
R - активное сопротивление; за счёт него
возникают тепловые потери в контуре.
17.
Падение напряжения на отдельных участкахцепи, представленной на рис.1,:
1
UC = q/ С = Idt U0C cos(ωt - φ - π/2);
С
UL = L (dI/dt) = U0L cos(ωt - φ+ π/2);
UR = U0R cos(ωt - φ).
U0L
ε0
φ
U0L -U0C
U0R
Рисунок 2
U0C
I0
18.
Резонанс•Из выражения (1) следует, что амплитуда вынужденных
колебаний зависит от частоты вынуждающей силы ω.
При ω → ω0, амплитуда колебаний увеличивается.
Частоту изменения вынуждающей силы, при которой
амплитуда
вынужденных
колебаний
достигает
максимального значения, называют резонансной.
Расчёты показывают, что
рез = 0
Подставив это значение частоты в выражение ( 1 ),
получим формулу амплитуды при резонансе:
I рез
ε
0
R
19.
Рисунок 3ω
Рисунок 4
20.
Мощность в цепи переменного тока• P(t) = ε(t) I(t), где
ε(t) = ε0cos t, I(t) = I0 cos( t - ).
• P(t) = I0 ε0 cos( t- )cos t = I0 ε0 (cos2 t .
.cos + sin t cos t sin )
1
.
• P =
I0 ε0 cos
2
Из векторной диаграммы (рис. 2) следует, что
ε0 cos = RI0. Поэтому
1 2
P RI0
2


















 physics
physics







