Затухающие и вынужденные колебания

1. Затухающие и вынужденные колебания

ВоГУ
Лекция 08
Затухающие и
вынужденные
колебания
Кузина Л.А.,
к.ф.-м.н., доцент
2019 г.
1

2. План

1. Затухающие колебания. Дифференциальное
уравнение, коэффициент затухания,
логарифмический декремент затухания,
добротность
2. Вынужденные колебания: дифференциальное
уравнение, амплитуда. Резонанс
2

3.

Затухающие колебания
Fупр. kx
На тело действуют силы:
По второму закону Ньютона:
- квазиупругая (возвращающая)
Fc r v rx - сопротивления среды
ma Fупр. Fc
r
k
x x x 0
m
m
x 2 x 02 x 0
Здесь β – коэффициент затухания;
0 – циклическая частота собственных
колебаний, то есть колебаний системы
в отсутствие сил сопротивления
a x
mx k x r x
Дифференциальное уравнение
затухающих колебаний, где
приняты обозначения:
r 2 k
0
2
m
m

4.

Затухающие колебания
x 2 x 02 x 0
Решение этого дифференциального
уравнения затухающих колебаний
при условии малости затухания
(при β < ω0):
x A0 e t cos t 0
02 2
Если затухание велико (β > ω0),
движение системы не имеет
колебательного характера и будет
апериодическим

5.

x 2 x 02 x 0 – дифф.ур-е
x A0 e t cos t 0 – решение дифф. уравнения
02 2 0 – частота затухающих меньше частоты собственных
A t A e t – амплитуда уменьшается по экспоненте
0
A t
A0
T
A t T

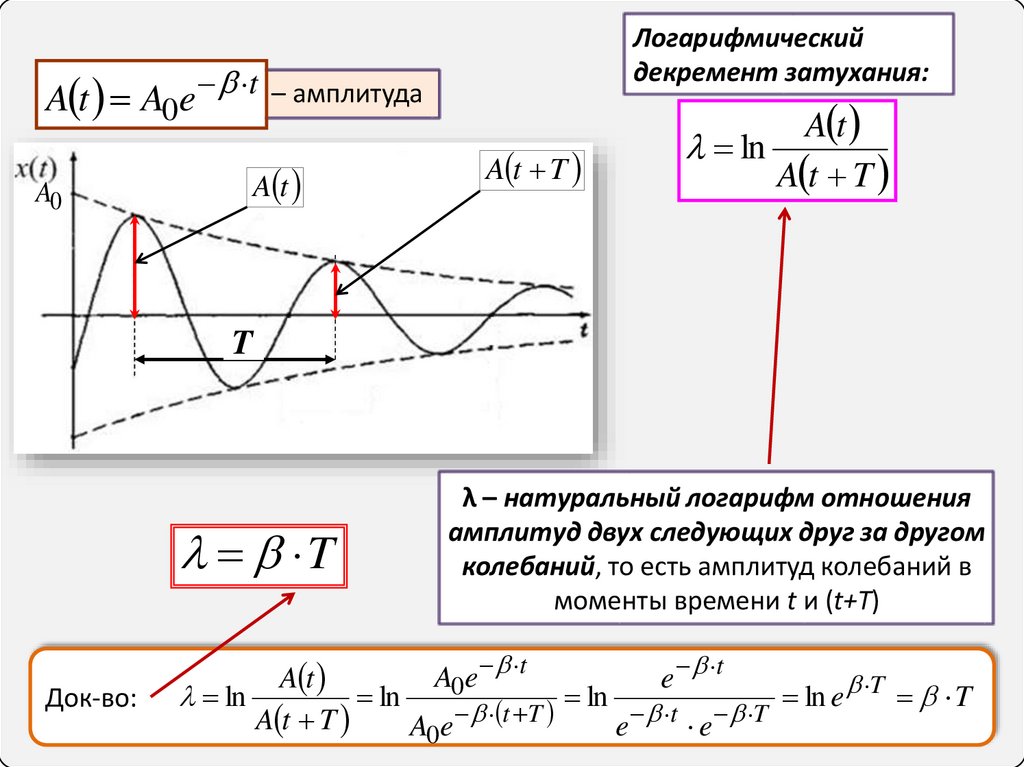
6.

Логарифмический
декремент затухания:
A t A0e t – амплитуда
A t
A0
A t T
A t
ln
A t T
T
T
Док-во:
λ – натуральный логарифм отношения
амплитуд двух следующих друг за другом
колебаний, то есть амплитуд колебаний в
моменты времени t и (t+T)
A0e t
A t
e t
ln
ln
ln
ln e T T
A t T
A0e t T
e t e T

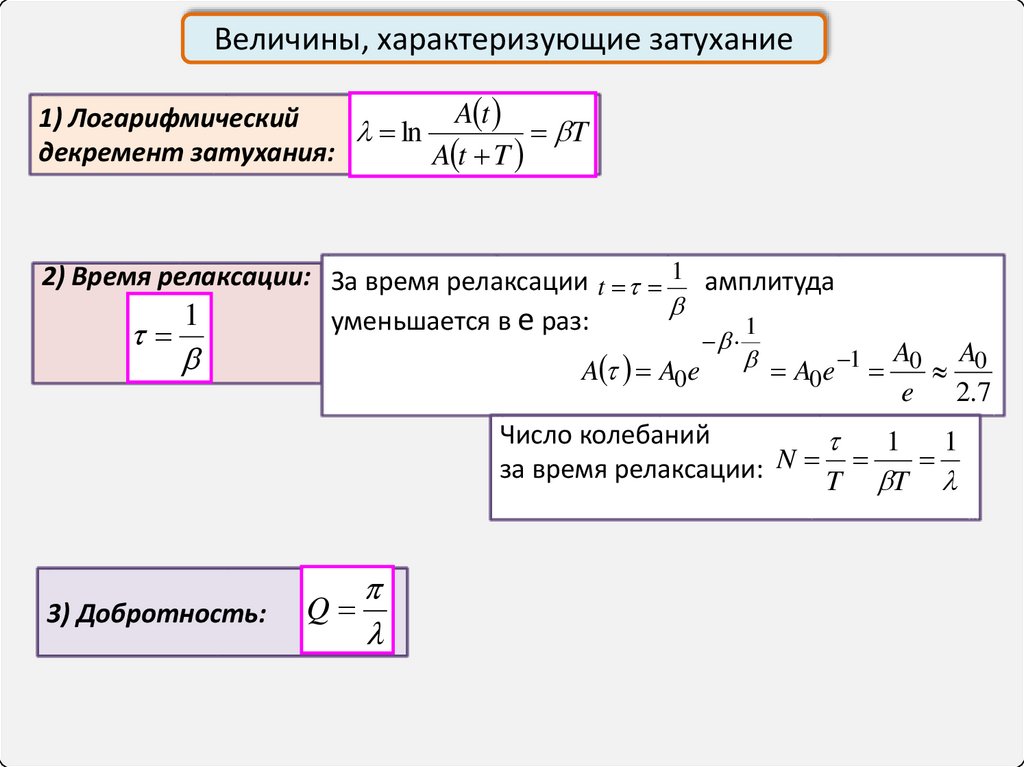
7.

Величины, характеризующие затухание
A t
1) Логарифмический
ln
T
декремент затухания:
A t T
2) Время релаксации: За время релаксации t 1 амплитуда
1
уменьшается в е раз:
1
A A0 e
A e 1 A0 A0
0
e
2.7
Число колебаний
1
1
N
за время релаксации:
T T
3) Добротность:
Q

8.

3) Добротность:
Q
Добротность пропорциональна числу
колебаний за время релаксации:
Q N
0 0
При условии малости затухания 0 : Q
T 2 2
Добротность обратно пропорциональна
относительной убыли энергии колебаний
за время, равное одному периоду:
W t
Q 2
W t W t T

9.

Вынужденные колебания
Чтобы при наличии сил сопротивления колебания не затухали,
колебательную систему нужно подпитывать энергией, - например, с
помощью вынуждающей периодической силы:
F F0 cos t
По второму закону Ньютона:
ma k x r v F0 cos t
r
k
F0
x x
cos t
m
m
m
x 2 x 02 x f0 cos t
x
Это - дифференциальное уравнение
вынужденных колебаний, где
приняты обозначения:
r
2
m
2
0
k
m
f0
F0
m

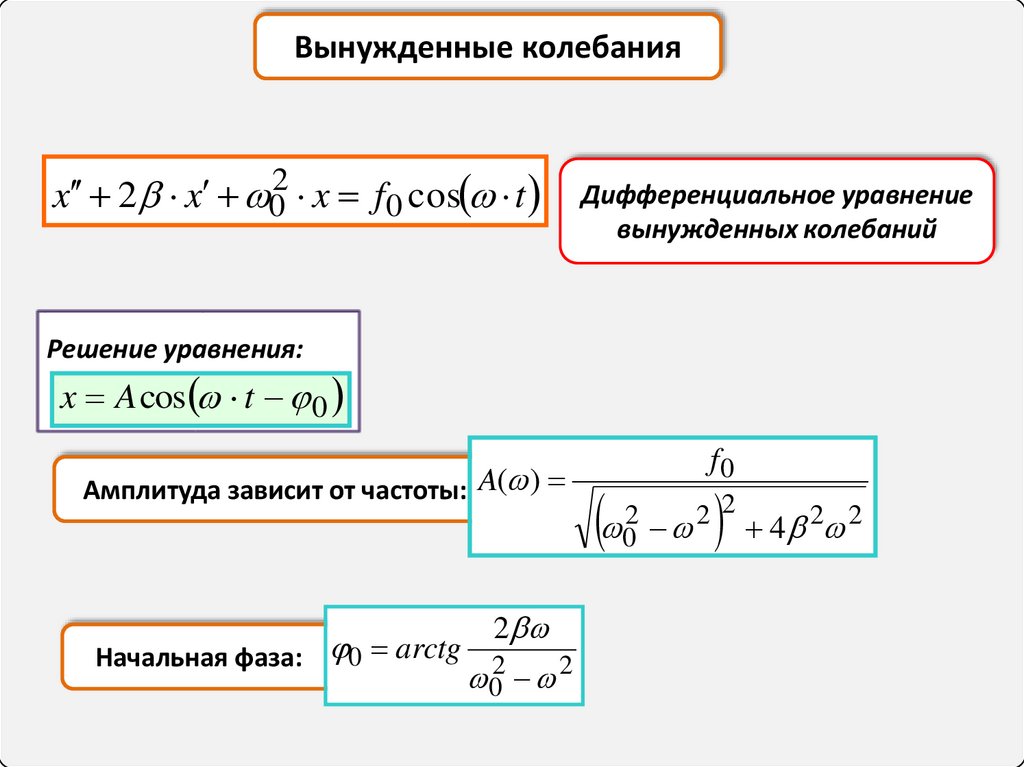
10.

Вынужденные колебания
x 2 x 02 x f0 cos t
Дифференциальное уравнение
вынужденных колебаний
Решение уравнения:
x A cos t 0
Амплитуда зависит от частоты: A( )
2
arctg
0
Начальная фаза:
02 2
f0
2
2 2
0
4 2 2

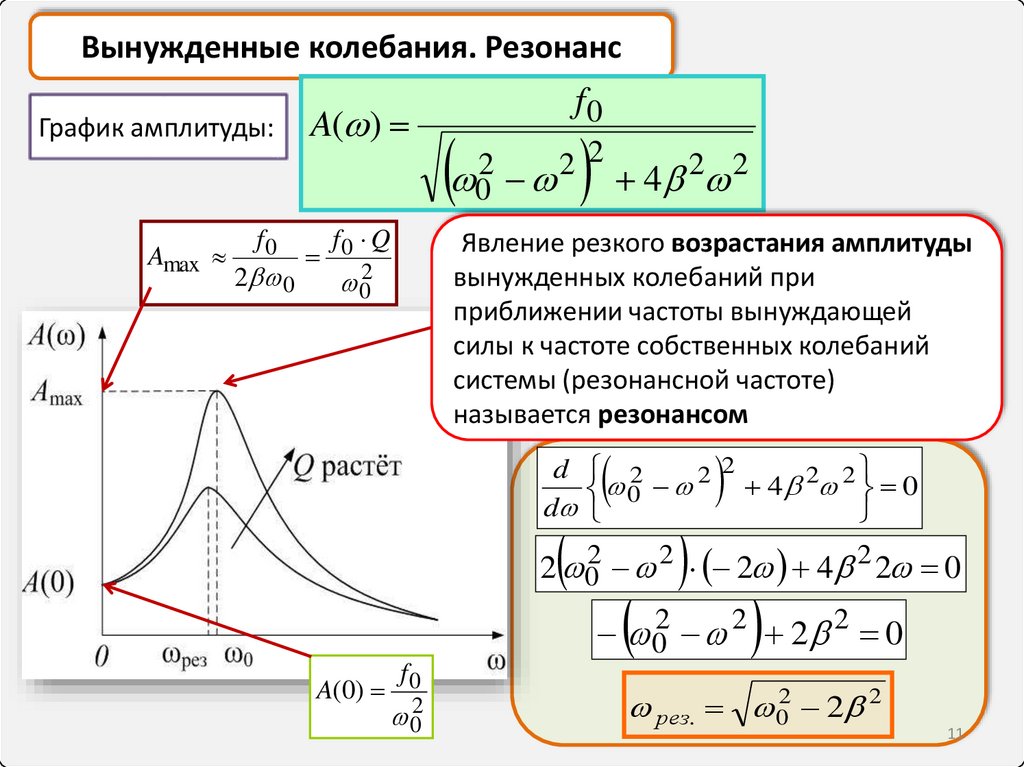
11.

Вынужденные колебания. Резонанс
График амплитуды:
Amax
f0
2 0
A( )
f Q
0
f0
2
2 2
0
4 2 2
Явление резкого возрастания амплитуды
вынужденных колебаний при
приближении частоты вынуждающей
силы к частоте собственных колебаний
системы (резонансной частоте)
называется резонансом
02
d 2
2 2
4 2 2 0
0
d
2 02 2 2 4 2 2 0
02 2 2 2 0
f
A(0) 0
02
рез. 02 2 2
11

12.

По этим ссылкам можно посмотреть видео
Свободные и вынужденные колебания:
https://youtu.be/093CzGsstv0
Затухающие колебания; запись песком:
https://youtu.be/ui0h6PfBvBM?list=PL9F96E1E5307658DB
Резонанс маятников; обмен энергией:
https://youtu.be/ux27Dovb9Fs
Биения на осциллографе:
https://youtu.be/RB51hhqLxCQ
12