Затухающие и вынужденные колебания

1.

Затухающие колебания.
Затухающими называются колебания амплитуда, которых уменьшается с течением
времени.
Пусть в системе действует диссипативная сила пропорциональная скорости колебаний
dx
F r
dt
где r – коэффициент сопротивления
Тогда дифференциальное уравнение затухающих колебаний примет вид
d 2 x r dx
2
0x 0
2
dt
m dt
решением которого будет уравнение затухающих колебаний
x X m0e
t
sin t
где – коэффициент затухания
r
2m

2.

x
X m X m0e
t
T
t
x X m0e
t
sin t

3.

Характеристики затухающих колебаний:
Частота затухающих колебаний:
1
02 2
Время релаксации – время в течение которого амплитуда колебаний
уменьшается в е раз
Декремент затухания- отношение амплитуд двух последующих колебаний за период.
X m( t )
e T
X m( t T )
Логарифмический декремент
ln T
Добротность системы – величина равная отношению энергии системы к затраченной
энергии за период.
0
Q
2

4.

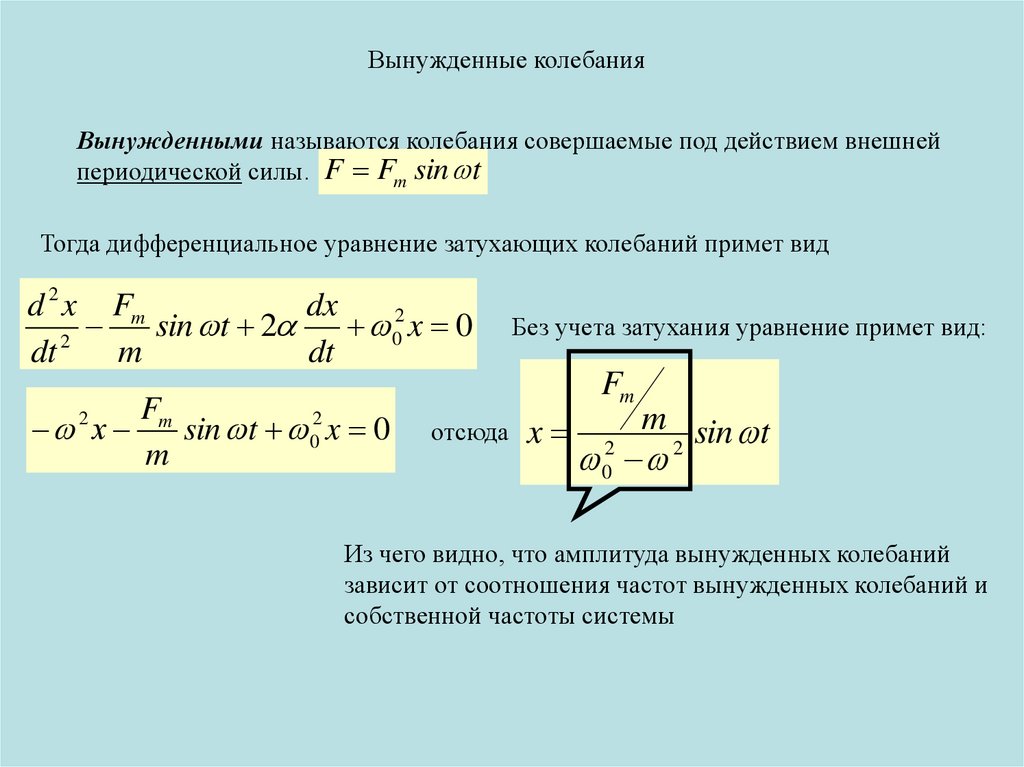
Вынужденные колебания
Вынужденными называются колебания совершаемые под действием внешней
периодической силы. F Fm sin t
Тогда дифференциальное уравнение затухающих колебаний примет вид
d 2 x Fm
dx
2
sin
t
2
0x 0
2
dt
m
dt
Fm
х
sin t 02 x 0
m
2
Без учета затухания уравнение примет вид:
Fm
отсюда
x
m sin t
02 2
Из чего видно, что амплитуда вынужденных колебаний
зависит от соотношения частот вынужденных колебаний и
собственной частоты системы

5.

Fm
Xm
Xm
m
02 2
Из графика видно, что амплитуда вынужденных
колебаний возрастает при приближении частоты
вынужденных колебаний к собственной частоте
системы.
Резонанс – явление резкого возрастания
амплитуды вынужденных колебаний при
совпадении частоты вынужденных колебаний
с собственной частотой системы.
0

6.

Xm
3
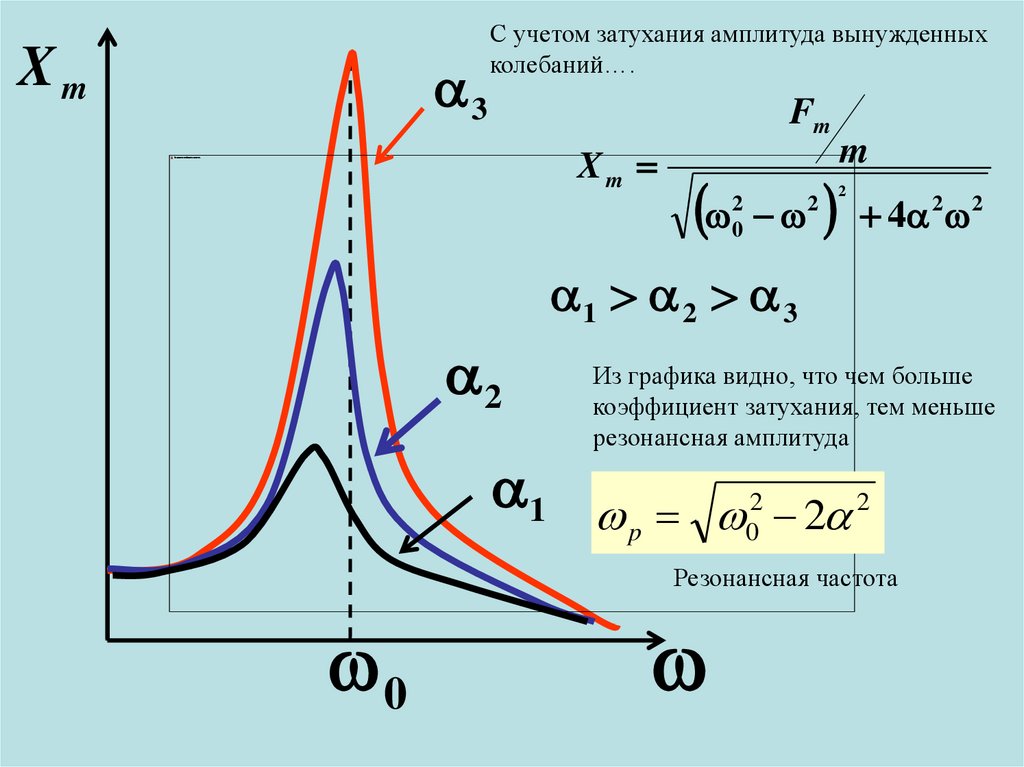
С учетом затухания амплитуда вынужденных
колебаний….
Fm
Xm
2
0
2
m
2
4 2 2
1 2 3
2
1
Из графика видно, что чем больше
коэффициент затухания, тем меньше
резонансная амплитуда
p 2
2
0
2
Резонансная частота
0