57a8a19bb5e64ab8b41eb4bf7185f7b7

1.

Затухающие и
вынужденные
колебания. Резонанс
вопросы

2.

Затухающие колебания – колебания, амплитуда
которых из-за потерь энергии реальной
колебательной системой с течением времени
уменьшается.
2
d x
dx
2
2
0 x 0
2
dt
dt
= const – коэффициент затухания,
в отсутствие потерь энергии = 0
x e u t
t
Свободные колебания реальной системы
всегда затухают
Закон затухания колебаний определяется
свойствами колебательных систем.
Затухания для маятника

3.

dx
Fтр r r
dt
2
d x
m 2 kx 0
dt
r- коэффициент
сопротивления.
Уравнение колебаний
пружинного маятника
2
d x
dx
Уравнение затухающих
m 2 r
kx 0 колебаний пружинного
dt
dt
маятника
x A0 e
r
t
2m
cos( t 0 )
Решение уравнения
Коэффициент затухания, амплитуда

4.

r
2m
Коэффициент затухания
r
2
0
2
2
0
2
4m
2
циклическая частота затухающих колебаний.
A A0 e
t
Амплитуда затухающих
колебаний
Изменяется амплитуда во времени!!
Частота изменяется относительно собственной
(начальной) частоты системы (частоты свободных
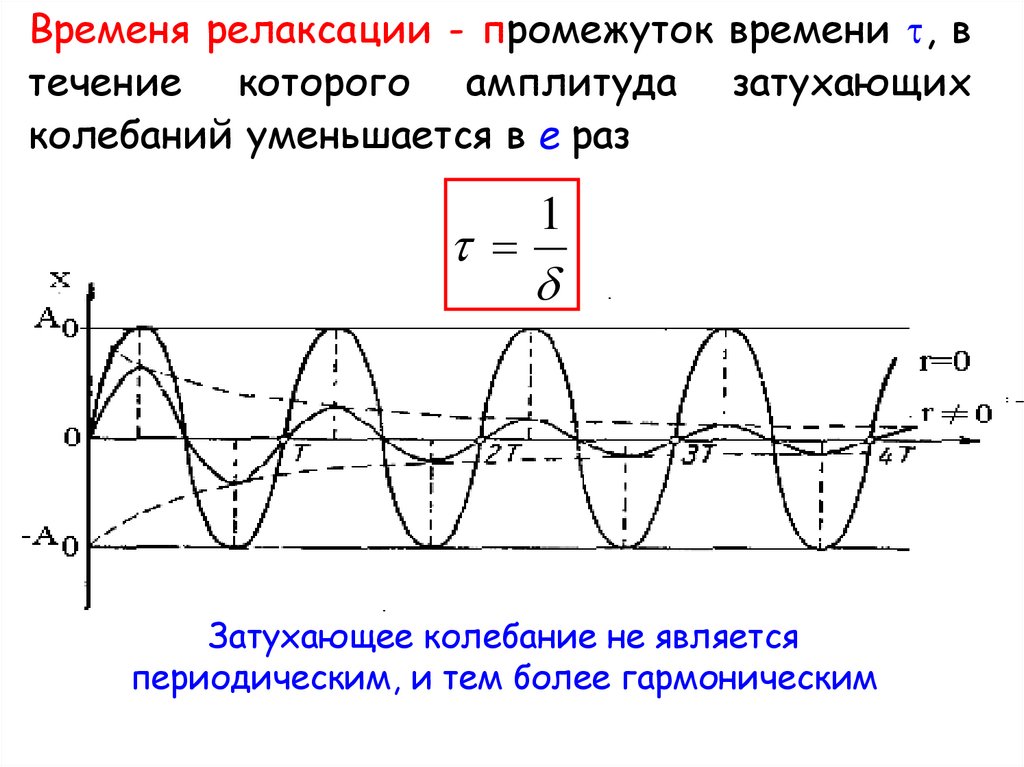
Время релаксации –
незатухающих колебаний)
график амплитуды

5.

Временя релаксации - промежуток времени , в
течение которого амплитуда затухающих
колебаний уменьшается в e раз
1
Затухающее колебание не является
периодическим, и тем более гармоническим

6.

Период
T
2
2
2
0
Декремент затухания отношение амплитуд 2-х
A t
T
e .
последовательных
A
t
T
колебаний:
Логарифмический декремент затухания:
2
A(t )
T
1
ln
T
A(t T )
Ne
Ne – число колебаний, совершаемых за время
ЛДЗ – const для данной колебательной
системы.

7.

Добротность:
0
Q N e
T0 2
Q равна с точностью до π числу колебаний Ne,
совершаемых системой за время релаксации τ.
Q пропорциональна отношению энергии W(t)
колеб. системы в момент времени t к убыли этой
энергии за промежуток времени от t до t + T
W t
Q 2
.
W t W t T

8.

От характера воздействия
1. Свободные колебания, возникающие при
однократном воздействии внешней силы
(первоначальном сообщении энергии) и при
последующем отсутствии внешних воздействий
на колебательную систему
2. Вынужденные – возникающие под действием
внешних, периодически изменяющихся сил (при
периодическом поступлении энергии извне к
колебательной системе)
3.Автоколебания – возникающие под действием
внутренних периодических сил(при периодическом
поступлении энергии от собственного источника
внутри колебательной системы)
вынужденные

9.

Вынужденные
колебания
–
незатухающие
колебания, возникающие в колебательной
системе под действием внешней периодической
силы,
изменяющейся
по
гармоническому
закону:
X t X 0 cos t
Для механических колебаний роль X(t) играет
внешняя вынуждающая сила
F F0 cos t
F

10.

Для простейшего пружинного маятника,
который действует внешняя сила:
на
2
d x
dx
m 2 kx r F0 cos t
dt
dt
Fупр
F
Fсопр
Дифференциальное
колебаний маятника:
уравнение
2
вын
вынужденных
F0
d x
dx
2
2
0 x cos t
2
dt
dt
m
r/2m =
k/m = 02

11.

Амплитуда установившихся вынужденных
колебаний:
F0
m
A
2
2 2
2 2
( 0 ) 4
Сдвиг фаз между смещением и вынуждающей
силой:
2
arctg 2
2
0

12.

В установившемся режиме вынужденные
колебания являются гармоническими,
происходят с частотой внешней гармонической
силы.

13.

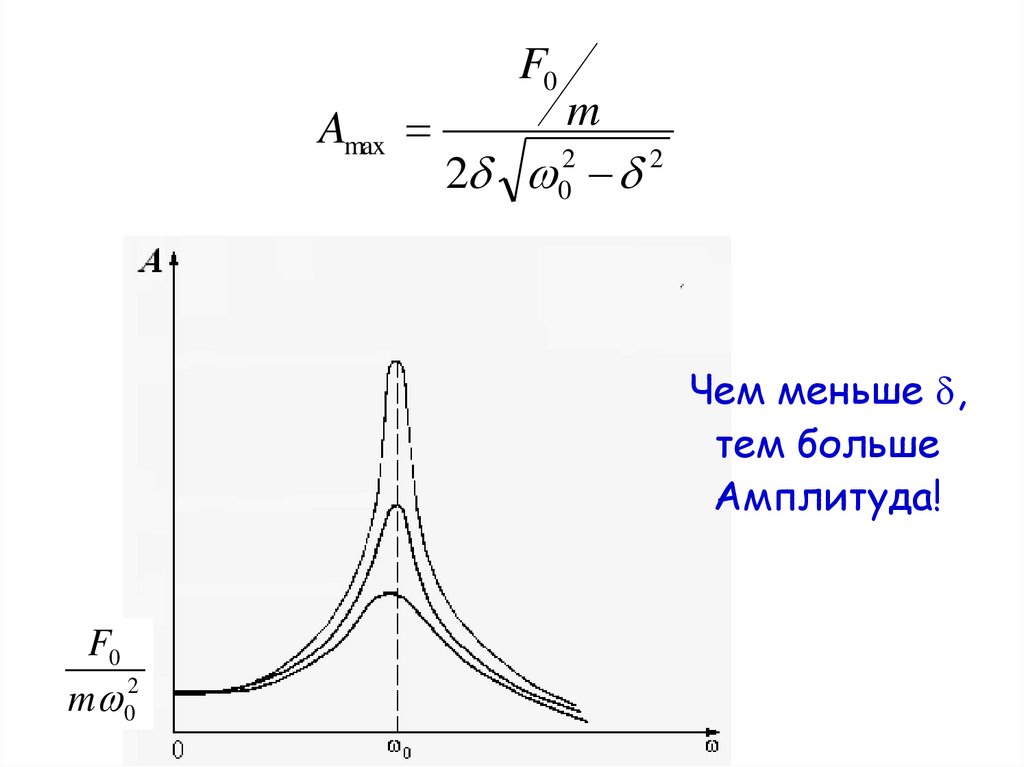
При некоторой частоте внешней силы –
резонансной частоте ωрез – амплитуда смещения
достигает максимального значения:
рез 2
2
0
2
Яв-ние резкого возрастания амплитуды
вынужденных колебаний при приближении
частоты вынуждающей силы к частоте, равной
или
близкой
собственной
частоте
колебательной
системы,
называется
механическим резонансом.

14.

F0
Amax
m
2
2
2 0
Чем меньше ,
тем больше
Амплитуда!
F0
m 02

15.

Автоколебания
колебательная
система,
совершающая незатухающие колебания за счёт
источника
энергии,
не
обладающего
колебательными
свойстваминазывается
автоколебательной системой.
Пример: часы с анкерным ходом, паровые
машины, двигатели внутреннего сгорания, отбойные
молотки, электрические звонки, смычёк для скрипки,
воздушные столбы в духовых инструментах, языки в
баянах и аккордеонах, голосовые связки при разговоре.