Колебания. Основные определения

1. Колебания

Пружинный маятник
Физический маятник
Математический маятник
Характеристики гармонических колебаний
Затухающие колебания
Вынужденные колебания. Резонанс

2. Основные определения

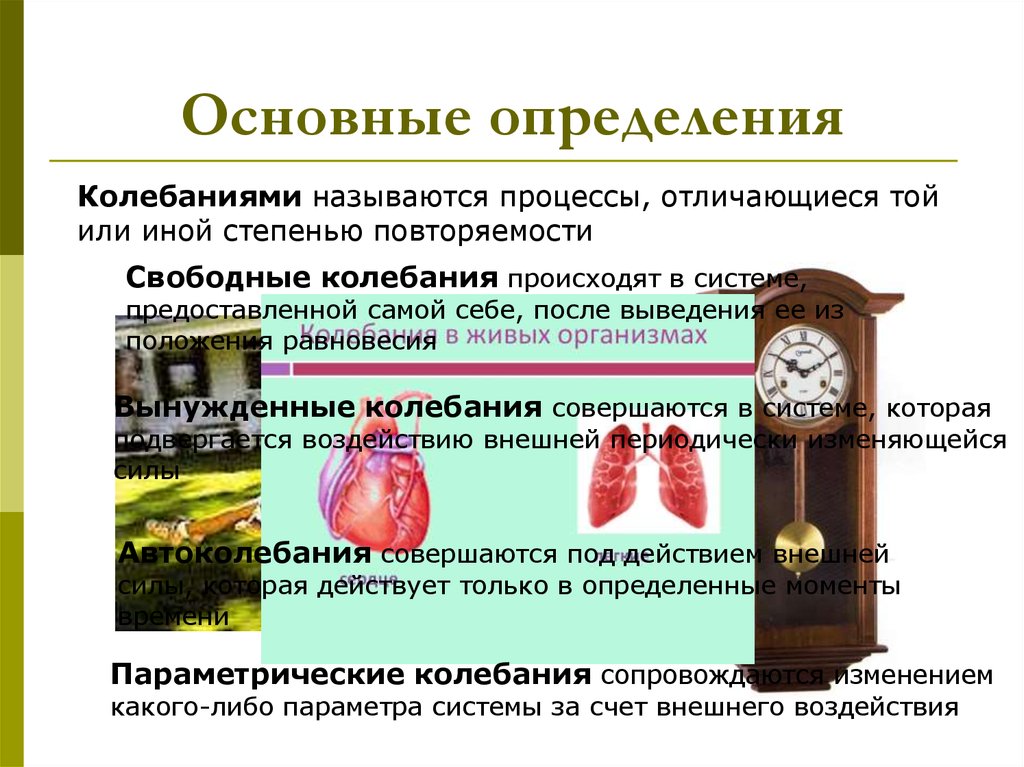
Колебаниями называются процессы, отличающиеся той
или иной степенью повторяемости
Свободные колебания происходят в системе,
предоставленной самой себе, после выведения ее из
положения равновесия
Вынужденные колебания совершаются в системе, которая
подвергается воздействию внешней периодически изменяющейся
силы
Автоколебания совершаются под действием внешней
силы, которая действует только в определенные моменты
времени
Параметрические колебания сопровождаются изменением
какого-либо параметра системы за счет внешнего воздействия

3. Пружинный маятник

4. Пружинный маятник

Дифференциальное уравнение
гармонических
колебаний
пружинного маятника:
2
d x k
x 0
2
dt
m
k
0
m
частота собственных колебаний
m
Т 2
k
период

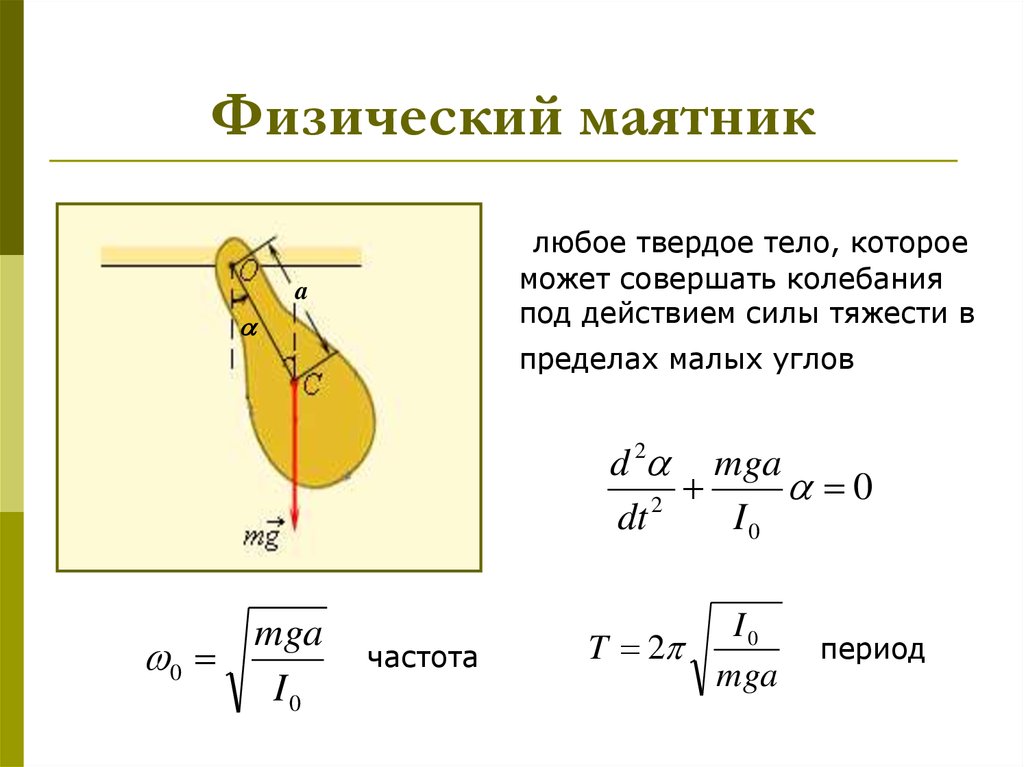
5. Физический маятник

любое твердое тело, которое
может совершать колебания
под действием силы тяжести в
a
пределах малых углов
d 2 mga
0
2
dt
I0
mga
0
I0
частота
I0
T 2
mga
период

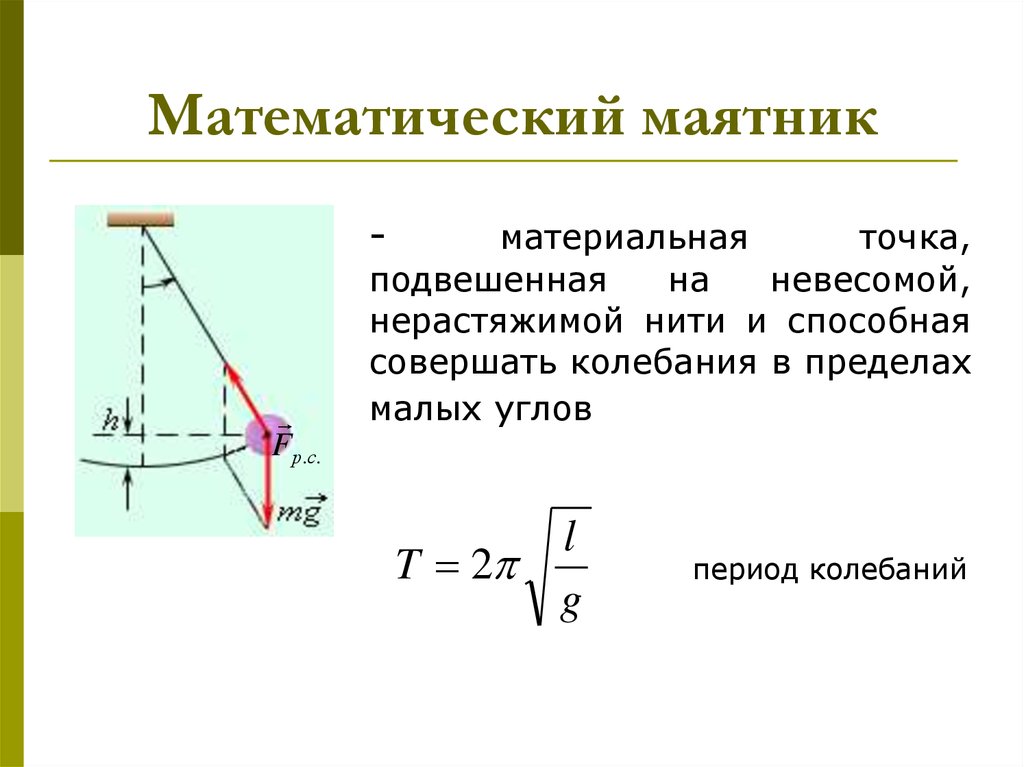
6. Математический маятник

-
Fр.с.
материальная
точка,
подвешенная
на
невесомой,
нерастяжимой нити и способная
совершать колебания в пределах
малых углов
l
T 2
g
период колебаний

7. Гармонические колебания

Пружинный
маятник
Физический
маятник
Математический
маятник
Колебательный
контур
k
0
m
k
x x 0
m
mga
0
J
mga
0
J
0
g
l
1
0
LC
g
0
l
1
Q
Q 0
LC

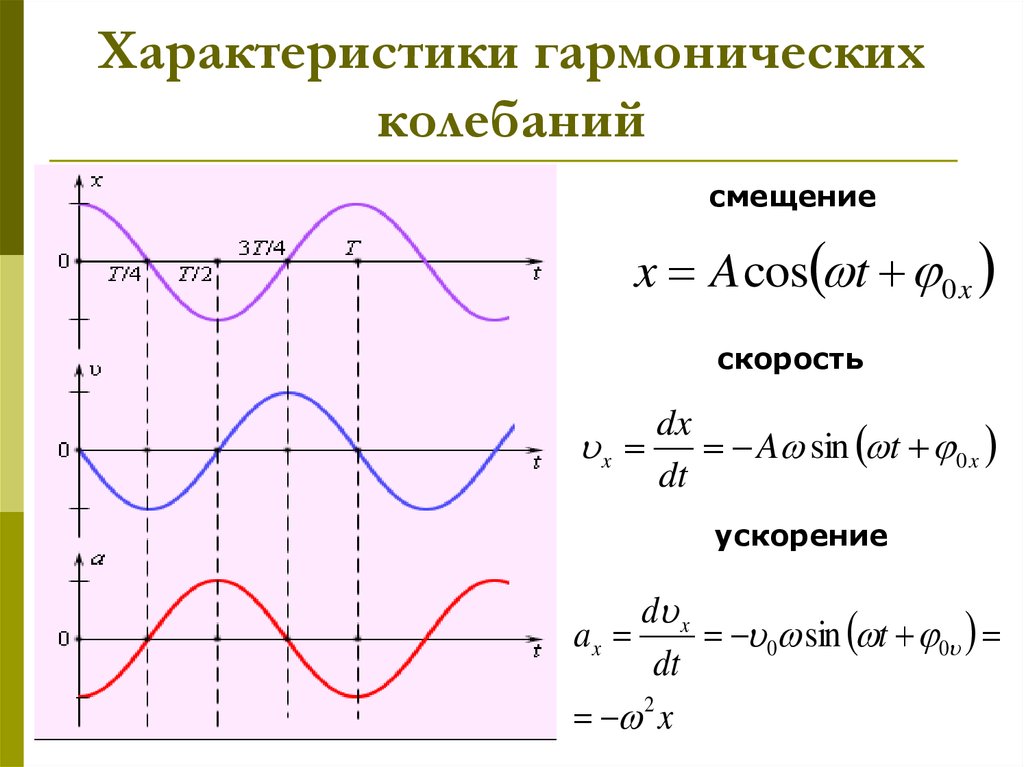
8. Характеристики гармонических колебаний

смещение
x A cos t 0 x
скорость
dx
x
A sin t 0 x
dt
ускорение
d x
ax
0 sin t 0
dt
2 x

9. Кинетическая и потенциальная энергия

x A cos( 0t )
dx
A 0 sin( 0t )
dt
d 2x
2
2
a
A
cos(
t
)
F
ma
m
0
0
0 x
2
dt
m 2 m A2 02
T
sin 2 ( 0t )
2
2
x
m 02 x 2 m A2 02
Eпот Fdx
cos 2 ( 0t )
2
2
0
m A2 02
Eполн T Eпот
2

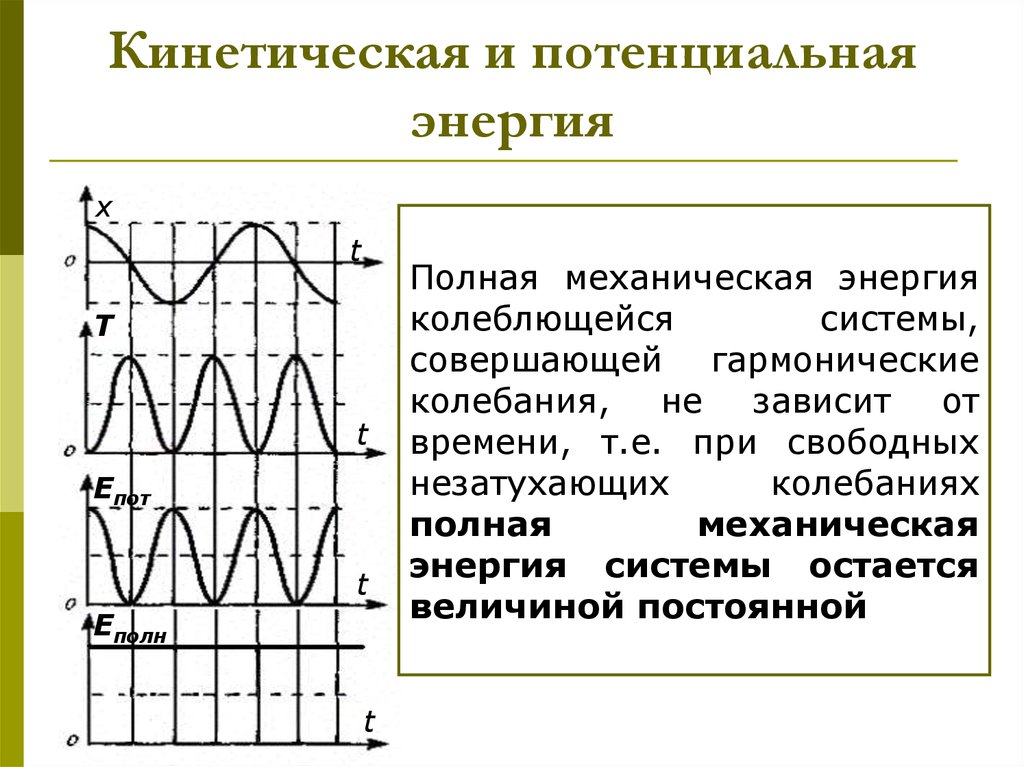
10. Кинетическая и потенциальная энергия

x
t
Т
t
Епот
t
Еполн
t
Полная механическая энергия
колеблющейся
системы,
совершающей гармонические
колебания, не зависит от
времени, т.е. при свободных
незатухающих
колебаниях
полная
механическая
энергия системы остается
величиной постоянной

11.

Затухающие колебания
d 2x
dx
2
2
0 x 0
2
dt
dt
0 2 2
x t A0 e t cos t 0
- частота затухающих колебаний
A(t )
e T
A(t T )
A(t ) A0 e t
декремент затухания
τ - время релаксации
1
A(t )
ln
T
A(t T )
логарифмический
коэффициент затухания

12. Вынужденные колебания

F0
d 2x
dx
2
2
0 x cos t
2
dt
dt
m
0x= x- F – сдвиг фаз между
смещением
силой:
A
и
вынуждающей
F0
m 0
2
4
2 2
2
2
x A cos t 0 x
2
tg 0 x 2
0 2
амплитуда вынужденных
колебаний

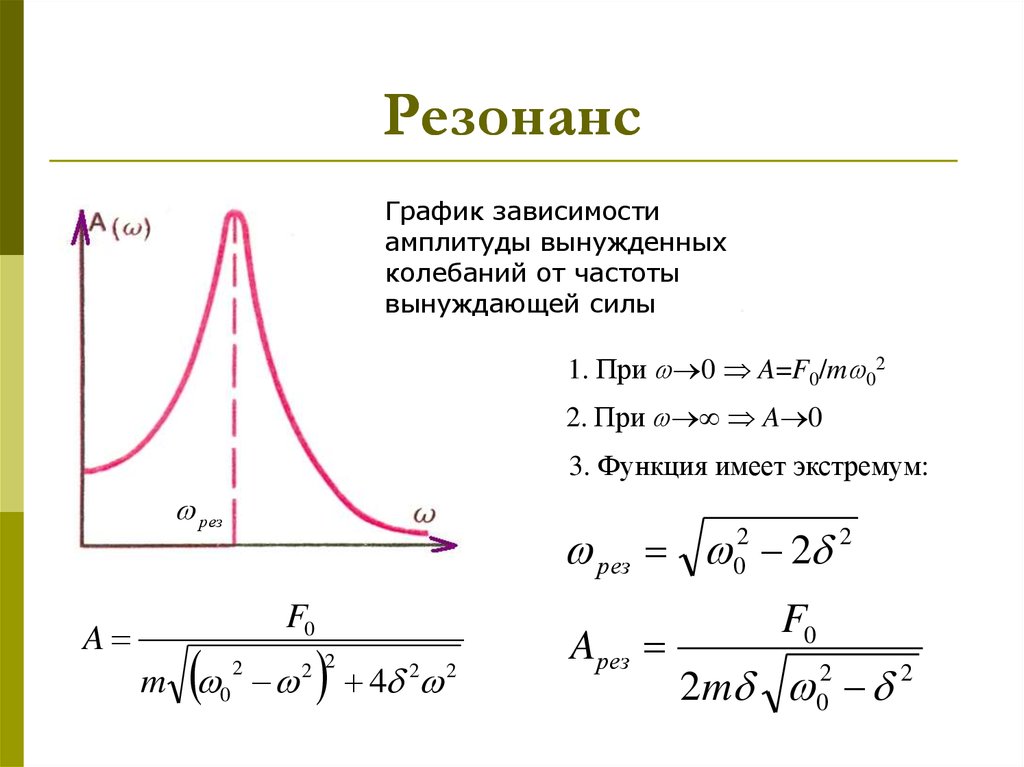
13. Резонанс

График зависимости
амплитуды вынужденных
колебаний от частоты
вынуждающей силы
рез
рез
1. При 0 A=F0/m 02
2. При A 0
3. Функция имеет экстремум:
рез
A
рез 02 2 2
F0
m 0
2
4
2 2
2
2
Aрез
F0
2m 02 2

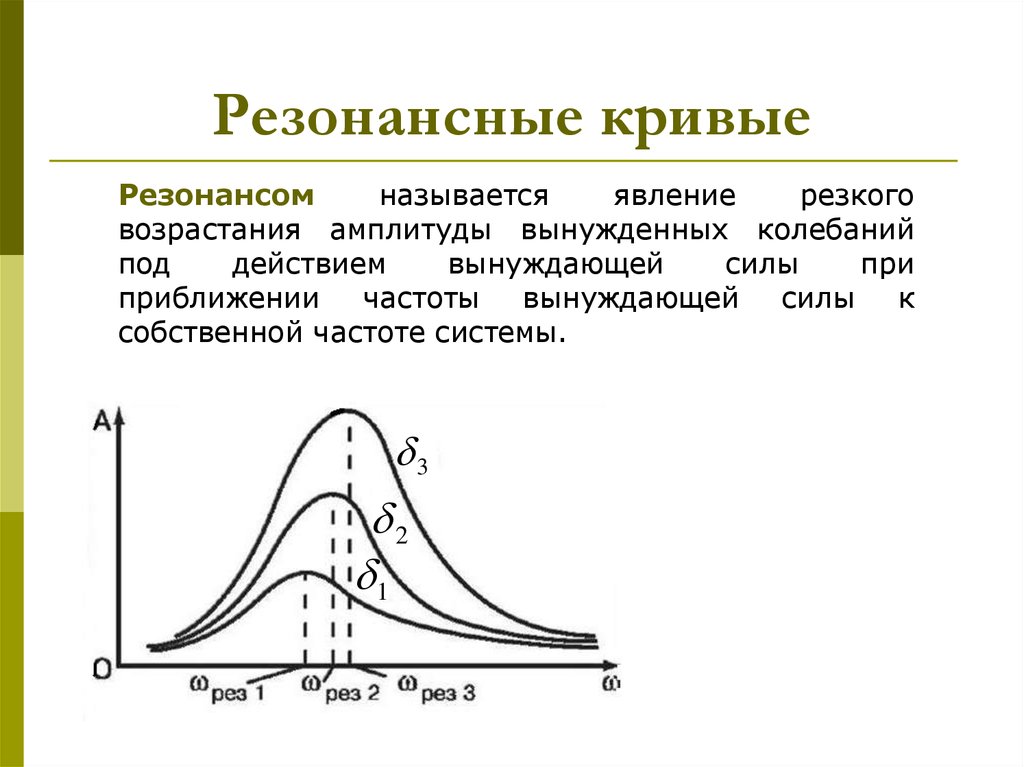
14. Резонансные кривые

Резонансом
называется
явление
резкого
возрастания амплитуды вынужденных колебаний
под
действием
вынуждающей
силы
при
приближении частоты вынуждающей силы к
собственной частоте системы.
3
2
1