Similar presentations:
Свободные затухающие и вынужденные колебания
1. Лекция 6. «Свободные затухающие и вынужденные колебания»
• Свободные затухающие колебания• Декремент и логарифмический декремент
колебаний
• Установившиеся и вынужденные колебания
• Механический резонанс
А.С. Чуев. 2020
1
2.
Знание законов заключается не в том,чтобы помнить их слова, а том, чтобы
постигать их смысл.
Цицерон
Все подобно всему в каком-нибудь
отношении.
Протагор
А.С. Чуев. 2020
2
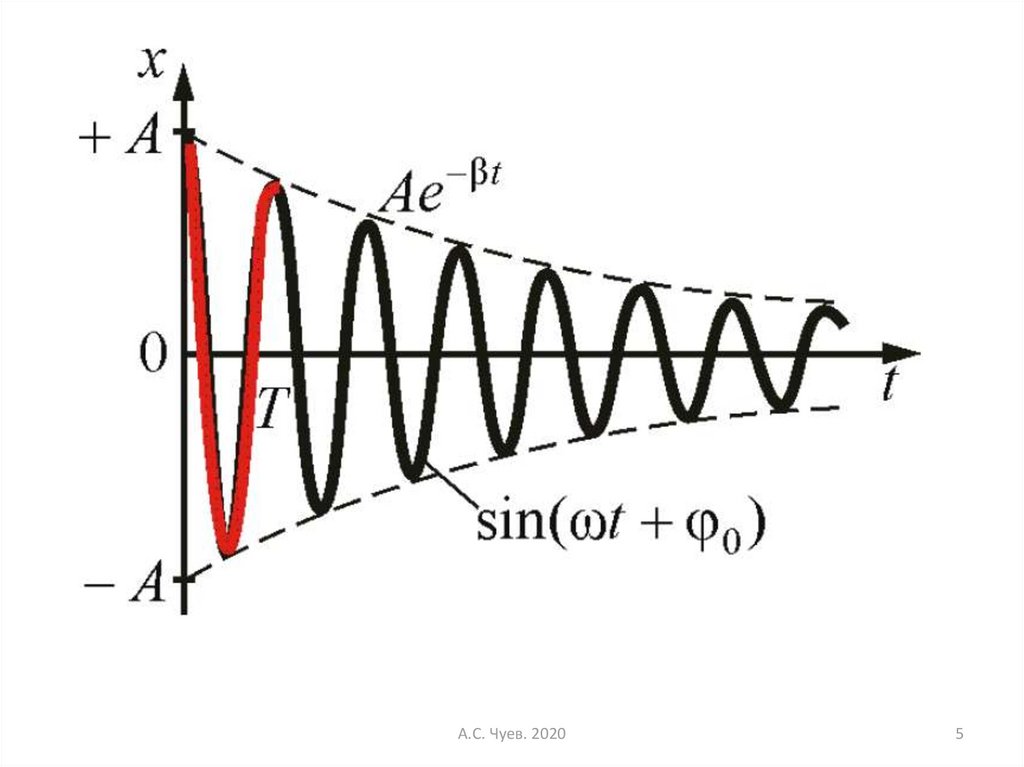
3. Свободные затухающие колебания
А.С. Чуев. 20203
4. Анимация
А.С. Чуев. 20204
5.
А.С. Чуев. 20205
6.
А.С. Чуев. 20206
7. Свободные затухающие колебания
Обозначим:А.С. Чуев. 2020
7
8.
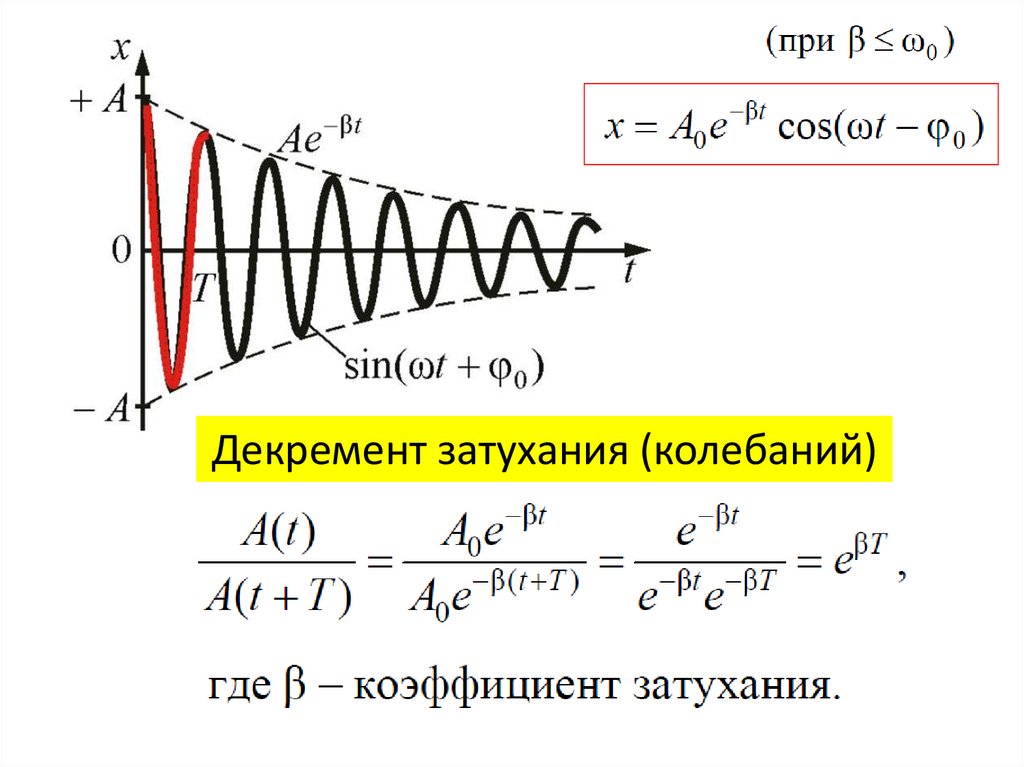
Декремент затухания (колебаний)9.
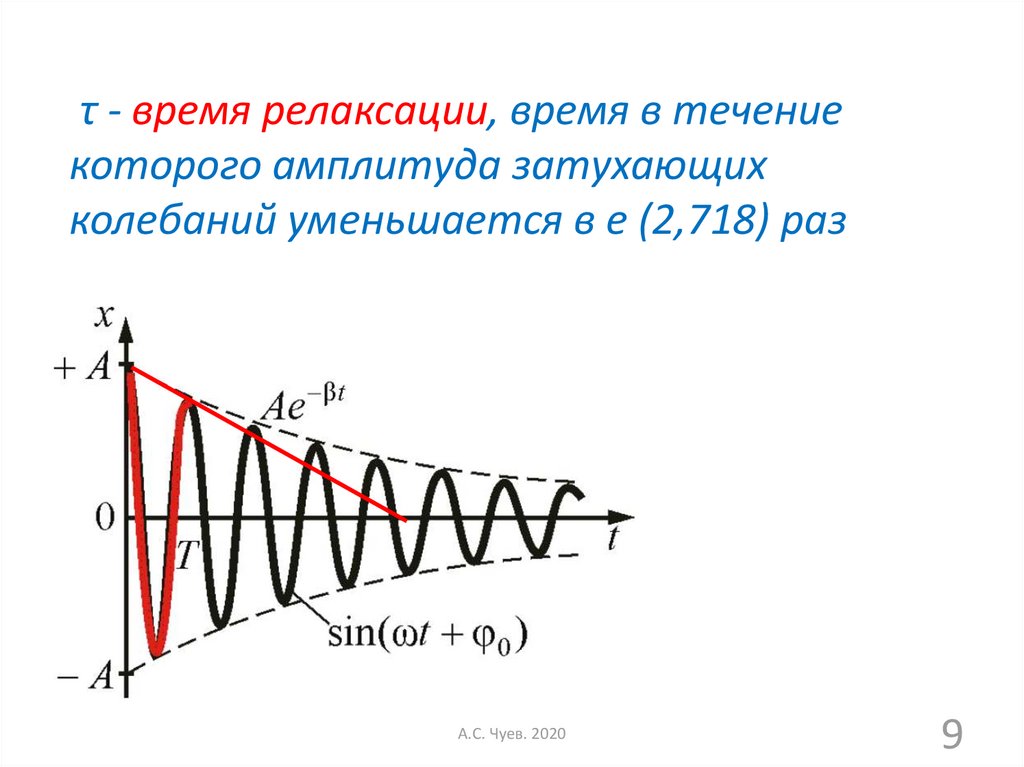
τ - время релаксации, время в течениекоторого амплитуда затухающих
колебаний уменьшается в e (2,718) раз
А.С. Чуев. 2020
9
10.
А.С. Чуев. 202010
11.
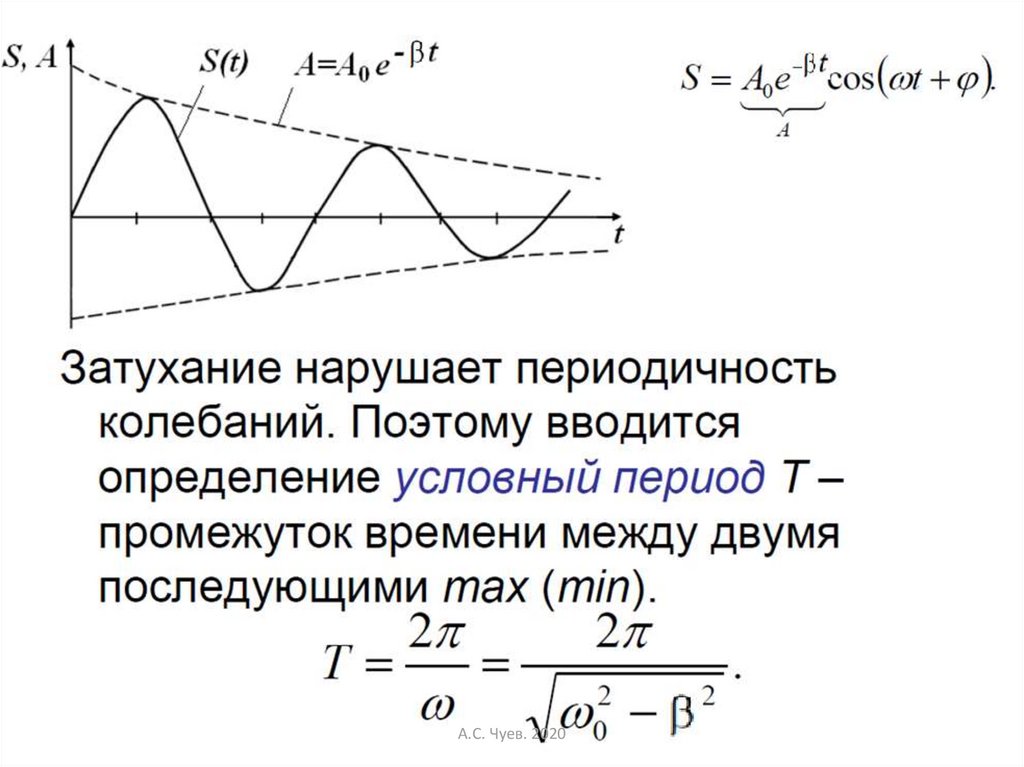
Вывод формулы, определяющей периодсвободных затухающих колебаний
Из формулы:
Следующие промежуточные выкладки можно опустить
А.С. Чуев. 2020
11
12.
Период затухающих колебанийА.С. Чуев. 2020
12
13.
Корни характ. уравнениямнимые
Корни характ. уравнения
действительные числа
А.С. Чуев. 2020
13
14.
Начало повторяетсяПроцесс затуханий колебаний
характеризует декремент затухания
(декремент колебаний) - отношение
амплитуды затухающих колебаний
через период
А.С. Чуев. 2020
14
15.
А.С. Чуев. 202015
16.
ФИЗИЧЕСКИЙ СМЫСЛдобротности колебательной системы
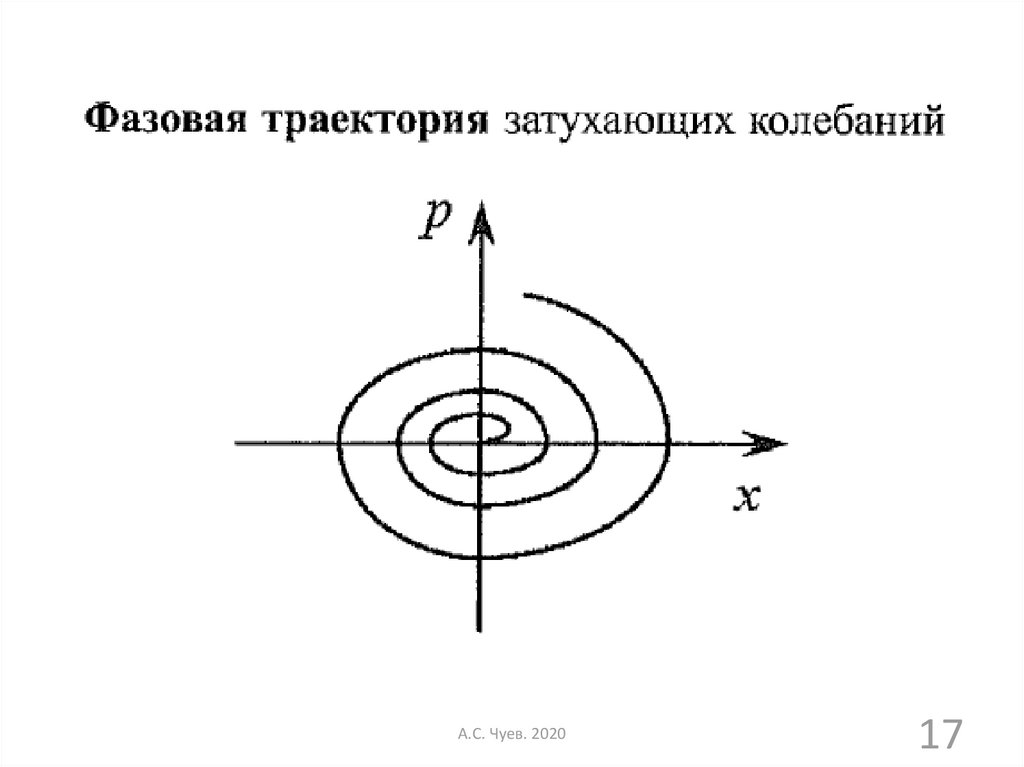
17.
А.С. Чуев. 202017
18.
А.С. Чуев. 202018
19.
Дальше частота внешней вынуждающейсилы Ω обозначается как ω
А.С. Чуев. 2020
19
20.
Вынужденные колебания(1)
(2)
Неоднородное линейное ДУ 2-го порядка
Решением неоднородного линейного ДУ является
сумма 2-х частей: решения однородного ДУ:
А.С. Чуев. 2020
20
21.
Это общее решение:и частное решение, не содержащее
произвольных постоянных
Предполагая, что решение имеет вид:
Дифференцируем его и подставляем в (2):
А.С. Чуев. 2020
21
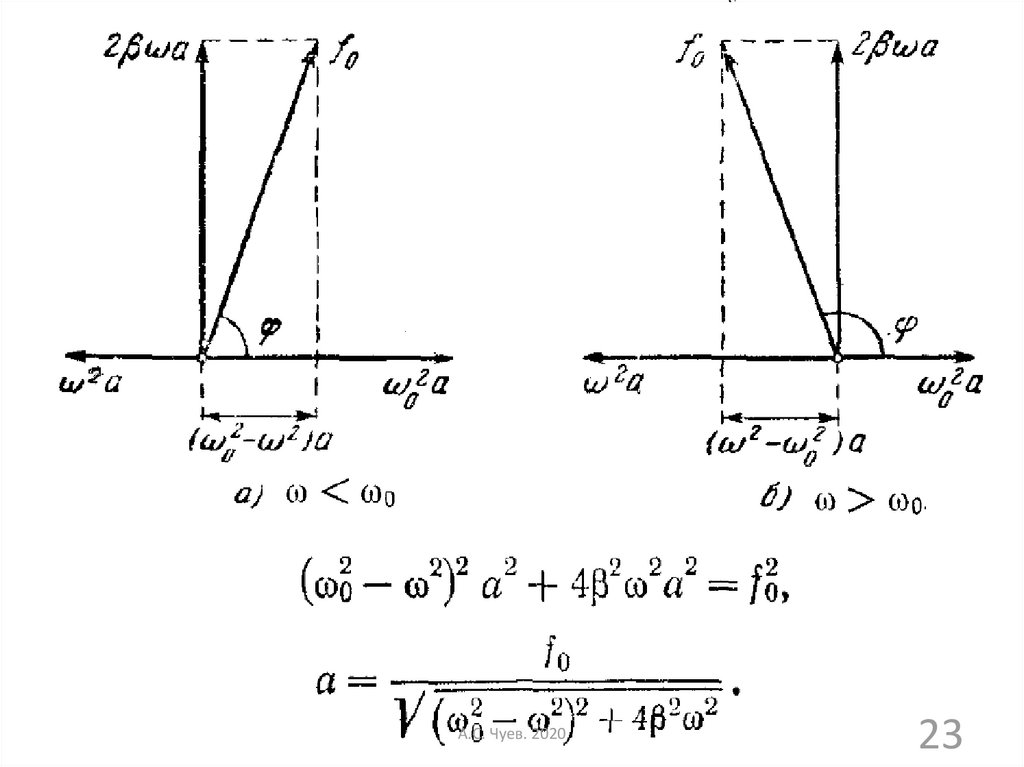
22.
Три составляющих уравнения (2):Наиболее простое решение - графическое
А.С. Чуев. 2020
22
23.
А.С. Чуев. 202023
24.
Из рисунка также следует:Подставив значения а и в частное
решение, получим:
А.С. Чуев. 2020
24
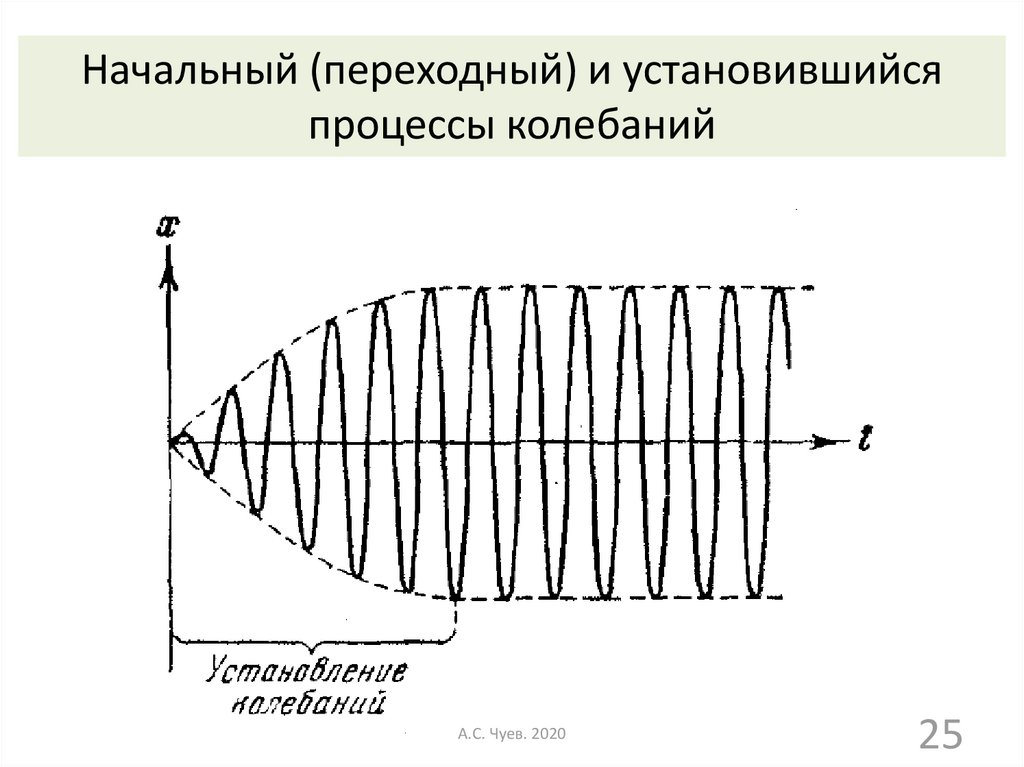
25.
Начальный (переходный) и установившийсяпроцессы колебаний
А.С. Чуев. 2020
25
26.
Общее решение определяет переходный процесс,поскольку присутствует экспоненциальный
множитель
Частное решение определяет установившиеся
вынужденные колебания. Частота вынужденных
колебаний определяется частотой колебаний
вынуждающей силы.
А.С. Чуев. 2020
26
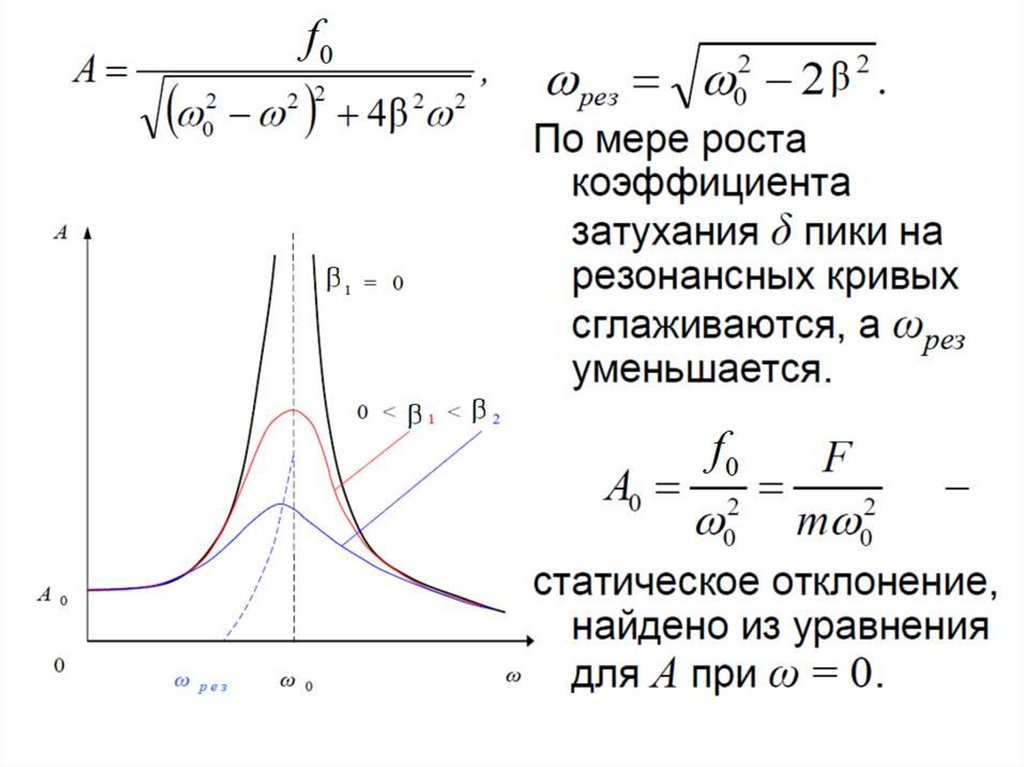
27.
Определив минимум подкоренноговыражения путем дифференц –ия и
приравнивания 0, получим:
А.С. Чуев. 2020
27
28.
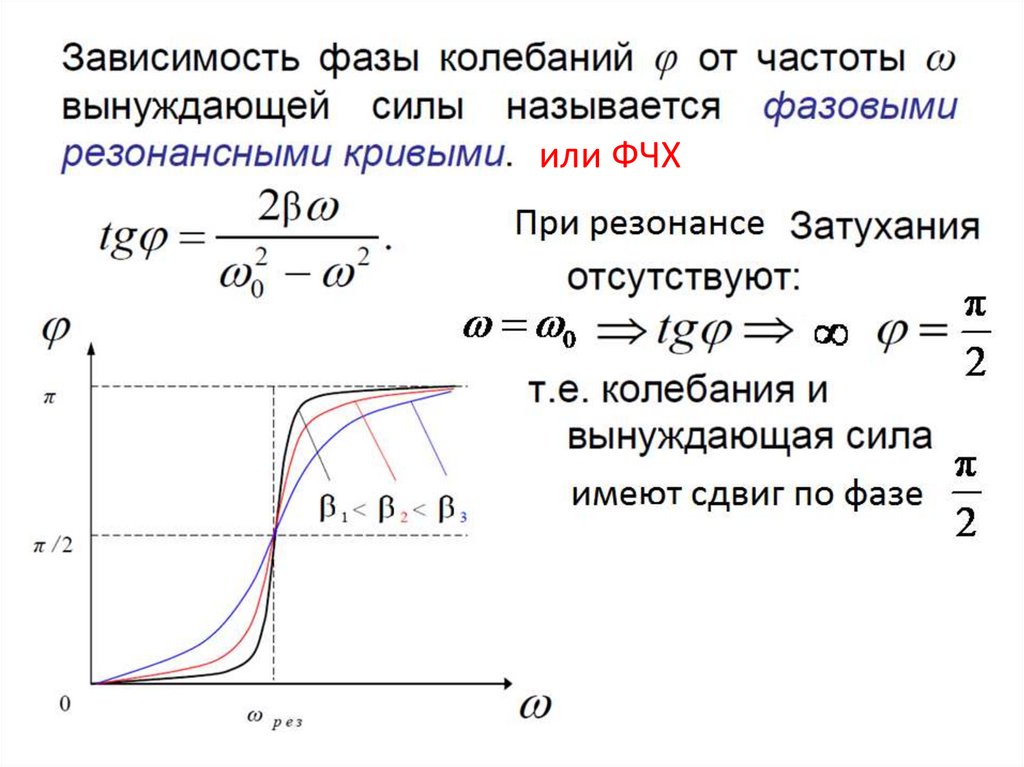
Резонанс29.
30.
или АЧХ31.
32.
или ФЧХ33.
Добротность КС – определяетсяотношением амплитуды колебаний
при резонансе к амплитуде
статического отклонения
Q
Aрез
Aст
34.
Автоколебания и параметрический резонанс- разобрать самостоятельно
А.С. Чуев. 2020
34
35.
А.С. Чуев. 202035
36.
К выполнению ДЗ по колебаниямl0
lГР
- х0
h0
h0
Положение равновесия
l0 - длина пружины в свободном состоянии;
h0 - дополнительное растяжение пружины в поле гравитации;
- х0 - начальное смещение массы от положения равновесия.
А.С. Чуев. 2020
36
mg
k
37.
F k(x h0 )m x mg - k(x h0 )
С учетом
mg kh0
m x kx
x(t) A cos( t 0 )
x (t) A sin( t 0 )
При t = 0
x0 Aсos 0
А.С. Чуев. 2020
v 0 A sin 0
37
38.
v0A sin 0
x0 Aсos 0
2
2
x v0
1
A A
Другой способ:
2
0
2
0
Отсюда
2
0
kx mv
kA
2
2
2
x0
0 arcсos
A
v0
A x
2
2
С учетом ω2=k/m
косинус функция четная, поэтому 0
дополнительно уточняем через тангенс
v0
0 arctg(
)
x0
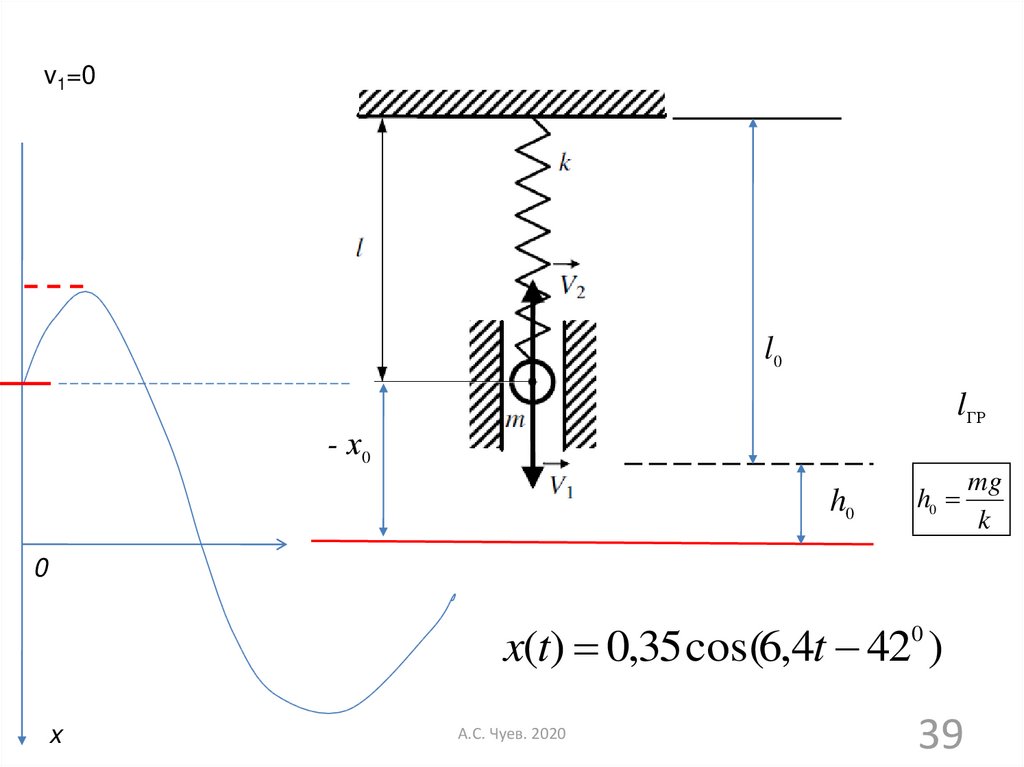
39.
v1=0l0
lГР
- х0
h0
h0
0
x(t) 0,35 cos(6,4t 42 )
0
x
А.С. Чуев. 2020
39
mg
k


























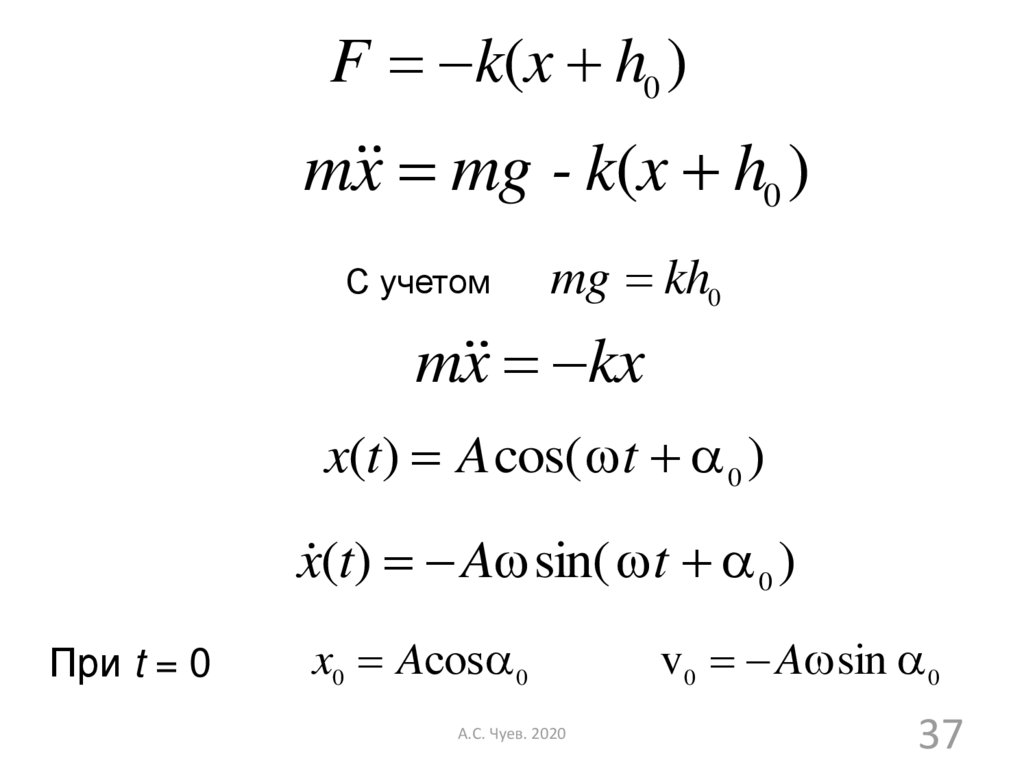


 physics
physics







