Similar presentations:
Сложение колебаний
1. 5.4 СЛОЖЕНИЕ КОЛЕБАНИЙ
Часто периодический процесс описывается некойнегармонической функцией F (t ) F (t T ) , где Т –
период. Можно строго показать, что такая функция есть
сумма гармонических колебаний различных частот i .
Метод разложения негармонической функции на
гармонические составляющие называется разложением
в ряд Фурье и является основным методом исследования
в радиотехнике.
2.
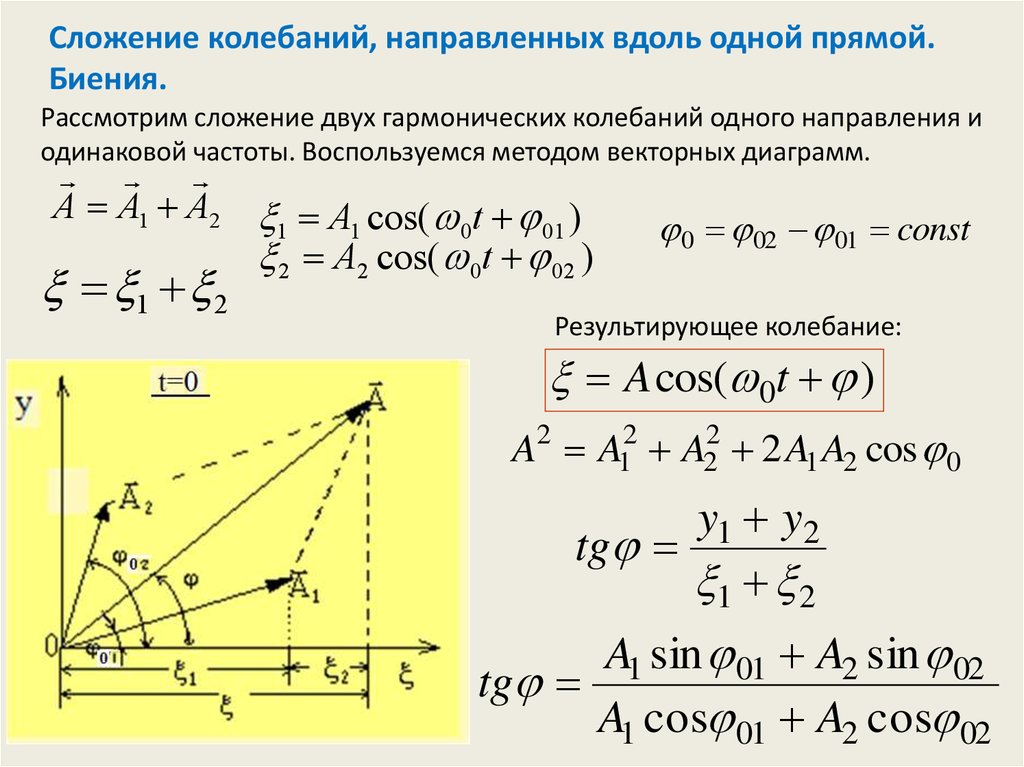
Сложение колебаний, направленных вдоль одной прямой.Биения.
Рассмотрим сложение двух гармонических колебаний одного направления и
одинаковой частоты. Воспользуемся методом векторных диаграмм.
A A1 A2
1 2
1 A1 cos( 0t 01 )
2 A2 cos( 0t 02 )
0 02 01 const
Результирующее колебание:
A cos( 0t )
A
2
2
A1
2
A2
2 A1 A2 cos 0
y1 y2
tg
1 2
A1 sin 01 A2 sin 02
tg
A1 cos 01 A2 cos 02
3.
Если01 02
Тогда разность фаз
колебаний:
, результирующее колебание будет негармоническим.
2 1 ( 02 01 )t ( 02 01 )
Рассмотрим случай близких частот, когда
01 ; 02
Пусть
Тогда:
A1 A2 A0
1 A0 cos t
2 A0 cos( )t
и
01 02 0
cos cos 2 cos
2
cos
2
1 2 A0 cos t cos( )t
2 A0 cos(
)t cos
t
2
2
t cos( t )
2 A0 cos
2
4.
Периодические изменения амплитуды результирующего колебания приналожении двух гармонических колебаний одинакового направления с
близкими частотами называются биениями.
2 A0 cos
t cos( t )
2
A(t ) 2 A cos
t
2
- амплитуда
биений
Биения возникают от того, что один
из двух сигналов постоянно отстаёт
от другого по фазе и в те моменты,
когда колебания происходят
синфазно, суммарный сигнал
оказывается усилен, а в те моменты,
когда два сигнала оказываются в
противофазе, они взаимно гасят
друг друга. Эти моменты
периодически сменяют друг друга
по мере того как нарастает
отставание.
2
Tб
- период пульсаций
амплитуды
5.
Сложение взаимно перпендикулярных колебаний.Фигуры Лиссажу.
x A1 cos 1t
Найдем траекторию движения м.т.,
колеблющейся одновременно вдоль осей OX и OY
по законам:
Вначале рассмотрим случай
y A2 cos( 2t 0 )
1 2
x
x
cos t sin t 1
A1
A1
2
y
cos( t 0 ) cos t cos 0 sin t sin 0
A2
2
x
y
x
cos 0 1 sin 0
A2 A1
A1
2
x
x
y
1 sin 0 cos 0
A1
A25
A1
6.
22
x 2
x
y
xy
1 sin 2 0 cos2 0 2
cos 0
A1 A2
A1
A1
A2
2
2
x
xy
y
2
2
cos 0 2 sin 0
2
A1 A2
A1
A2
(1)
- траектория
движения точки.
Это уравнение эллипса, оси которого повернуты относительно
осей OX,OY.
Рассмотрим частные случаи.
x2
xy
y2
а) 0 0 :
2
2 0;
2
A1 A2 A2
A1
y
x
0;
A2 A1
A2
y
x
A1
A2
tg
A1
7.
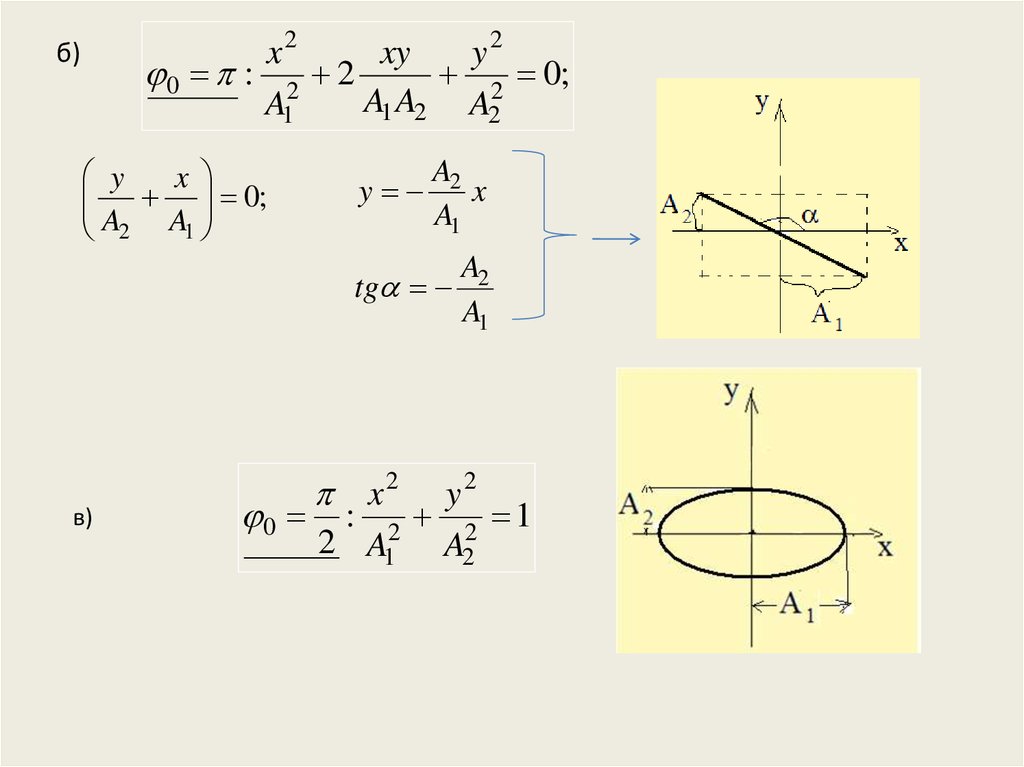
x2xy
y2
0 : 2 2
2 0;
A1 A2 A2
A1
б)
y
x
0;
A2 A1
y
A2
x
A1
A2
tg
A1
в)
x2
y2
0 : 2 2 1
2 A1 A2
8.
Рассмотрим случай близких частот, когда01 ; 02
и
x A1 cos t
y A2 cos t 0 A2 cos t (t )
(t ) t o - разность фаз складываемых колебаний медленно
меняется со временем по сравнению с изменением
самих фаз.
9.
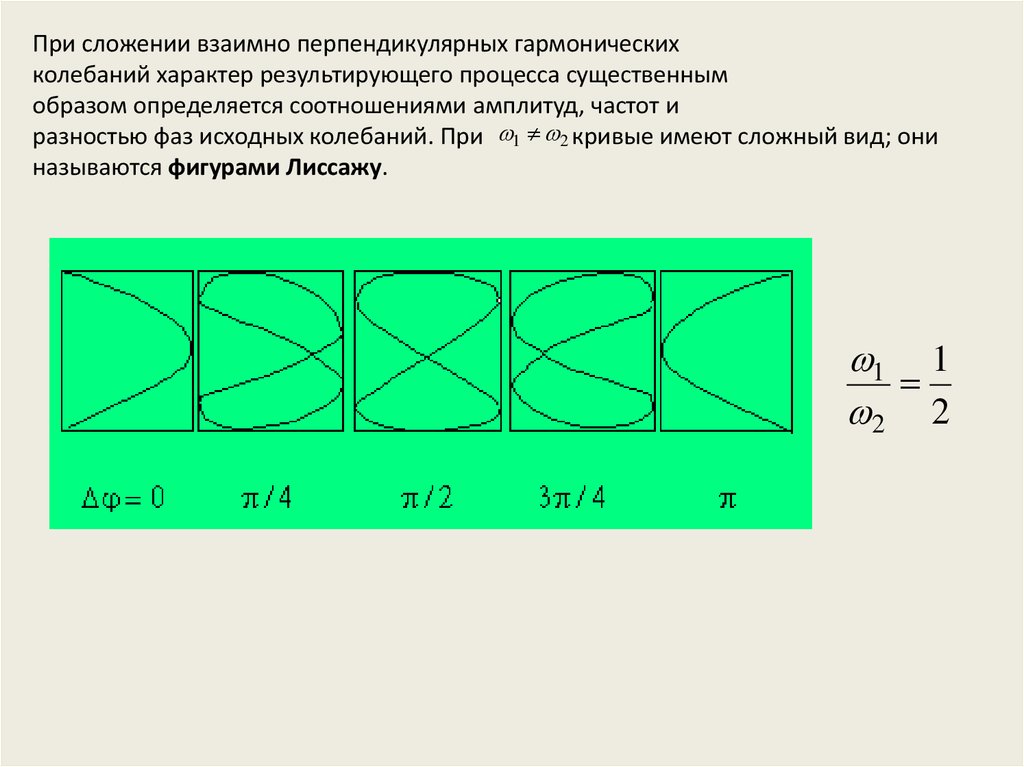
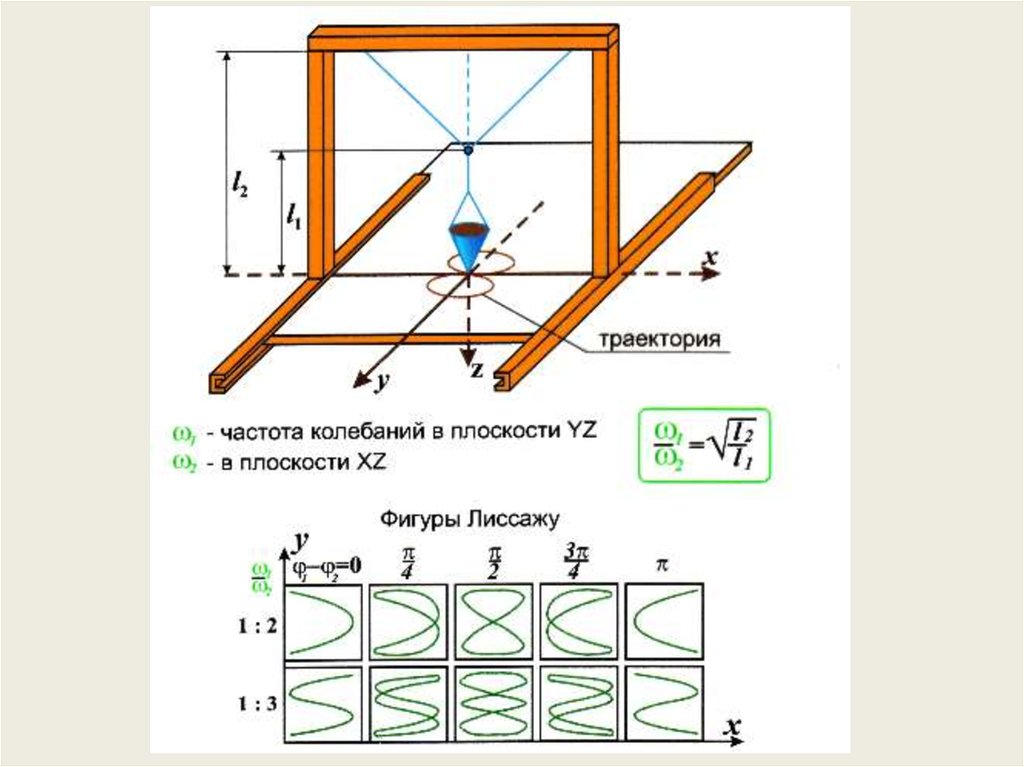
При сложении взаимно перпендикулярных гармоническихколебаний характер результирующего процесса существенным
образом определяется соотношениями амплитуд, частот и
разностью фаз исходных колебаний. При 1 2 кривые имеют сложный вид; они
называются фигурами Лиссажу.
1 1
2 2

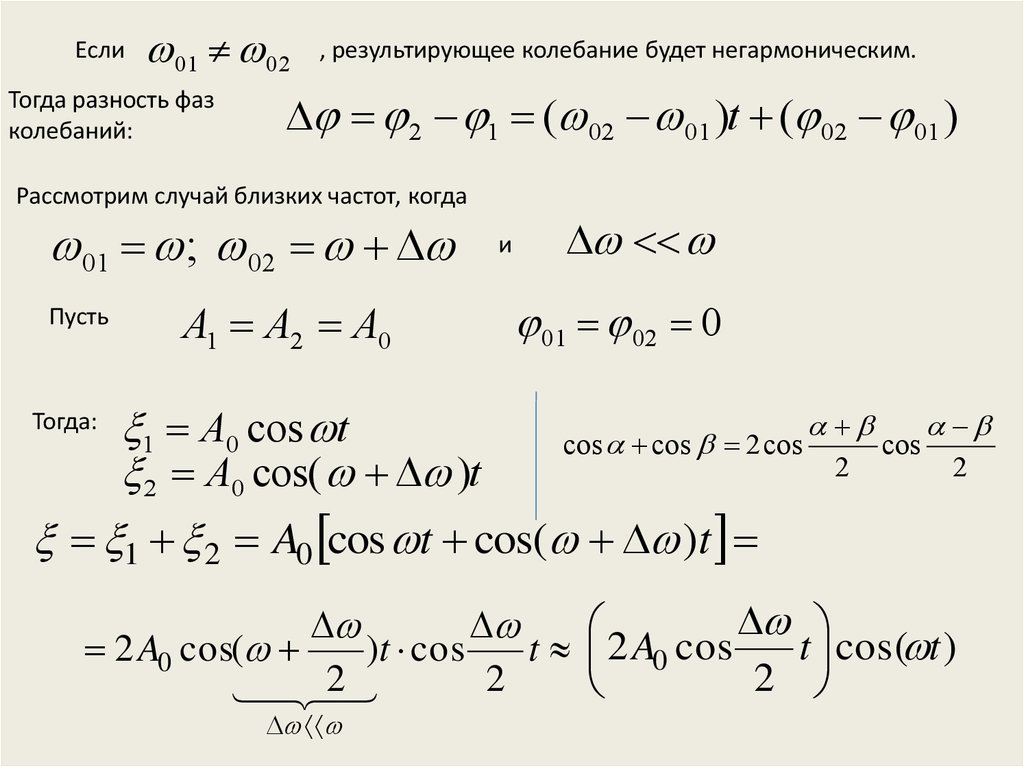




 physics
physics