Сложение гармонических колебаний. Тема 2

1.

Сегодня: пятница, 13 июня 2025 г.
ЛЕКЦИЯ 1 (часть 2)
Тема 2. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
2.1. Способы представления гармонических колебаний
2.2. Сложение гармонических колебаний. Биения CРC
2.3. Сложение взаимно перпендикулярных колебаний
CРC
2.4. Фигуры Лиссажу (частные случаи) СРС*

2.

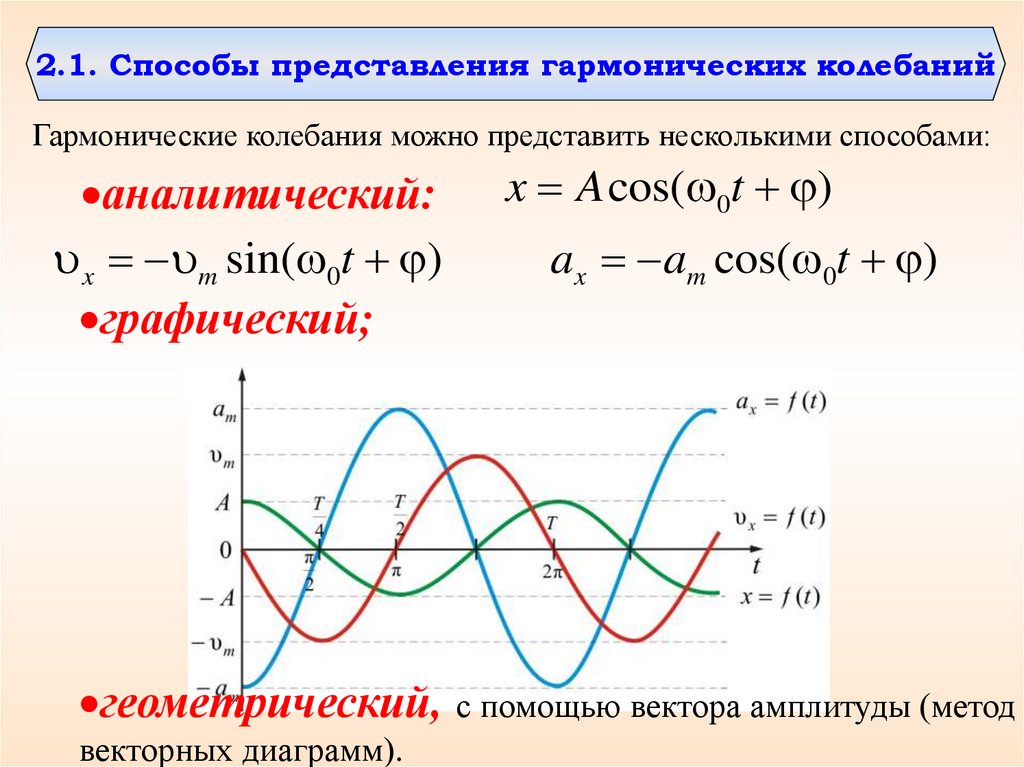
2.1. Способы представления гармонических колебаний
Гармонические колебания можно представить несколькими способами:
аналитический:
x m sin( 0t )
графический;
x A cos( 0t )
ax am cos( 0t )
геометрический, с помощью вектора амплитуды (метод
векторных диаграмм).

3.

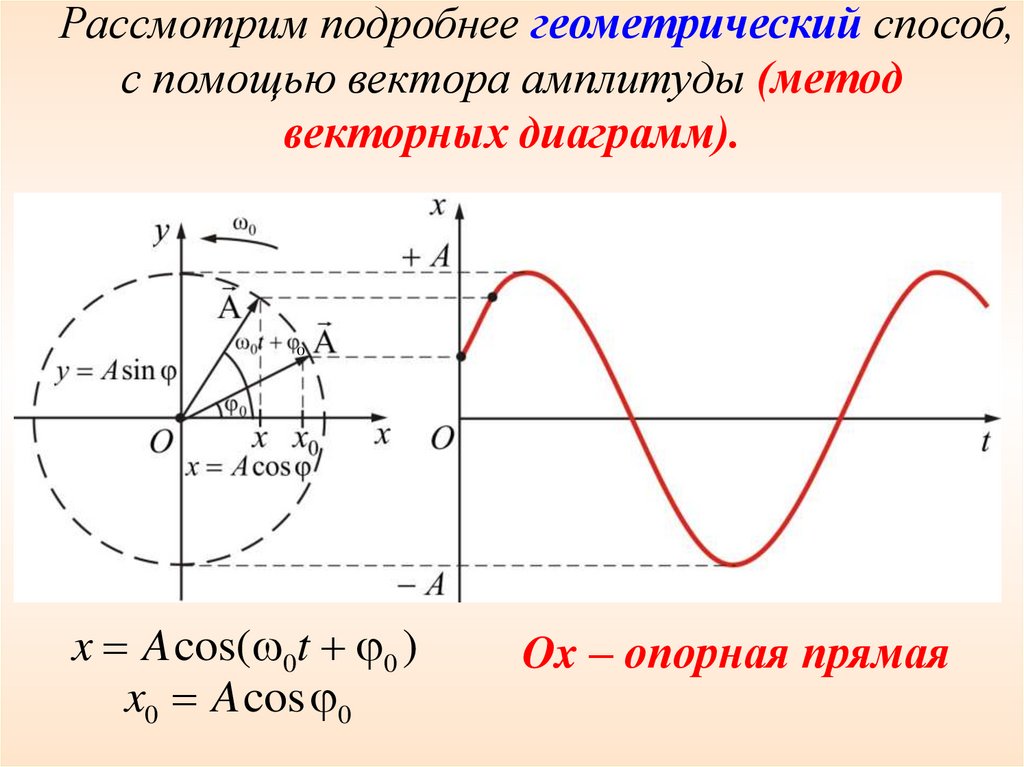
Рассмотрим подробнее геометрический способ,
с помощью вектора амплитуды (метод
векторных диаграмм).
0
x A cos( 0t 0 )
x0 A cos 0
Ox – опорная прямая

4.

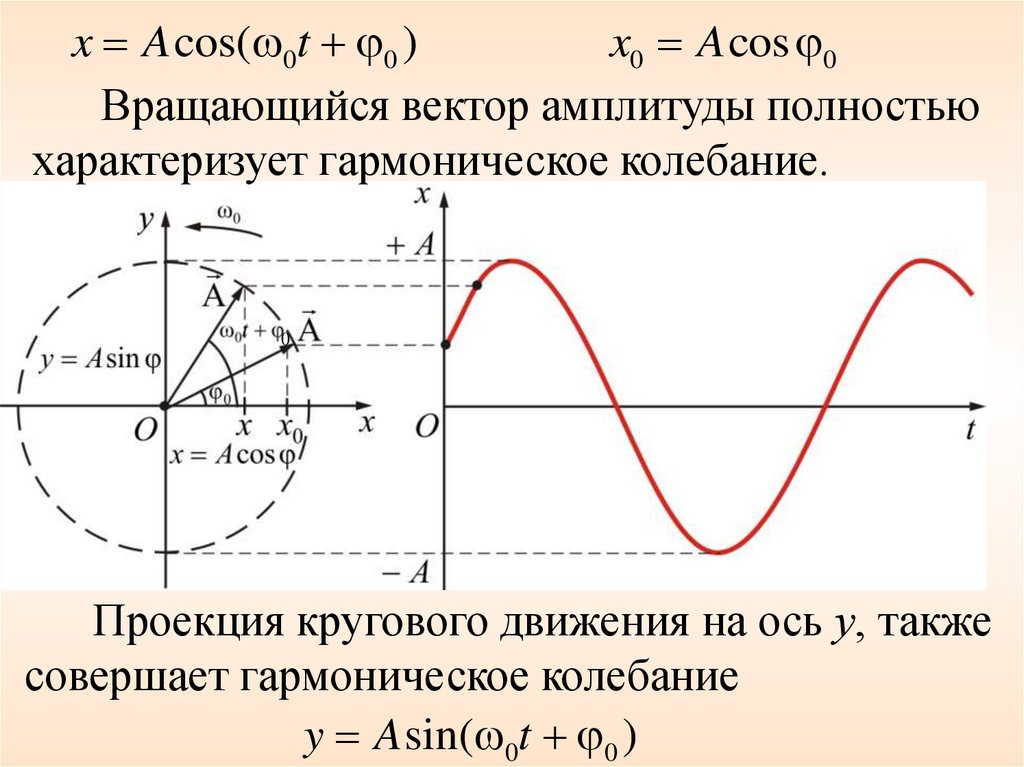
x A cos( 0t 0 )
x0 A cos 0
Вращающийся вектор амплитуды полностью
характеризует гармоническое колебание.
0
Проекция кругового движения на ось у, также
совершает гармоническое колебание
y A sin( 0t 0 )

5.

2.2. Сложение гармонических колебаний. Биения
Круговая волна на
поверхности жидкости,
возбуждаемая гармонически
колеблющимся шариком.
Интерференция между двумя
круговыми волнами от
точечных источников,
колеблющихся в фазе друг с
другом. На поверхности
жидкости образуются узловые
линии, в которых колебание
max или отсутствует.

6.

Пусть точка одновременно участвует в двух
гармонических колебаниях одинакового периода,
направленных вдоль одной прямой.
(2.2.1)
x1 A1 cos( 0t 1 )
x2 A2 cos( 0t 2 )
Такие два колебания
называются
когерентными,
их разность фаз не
зависит от времени:
2 1 const

7.

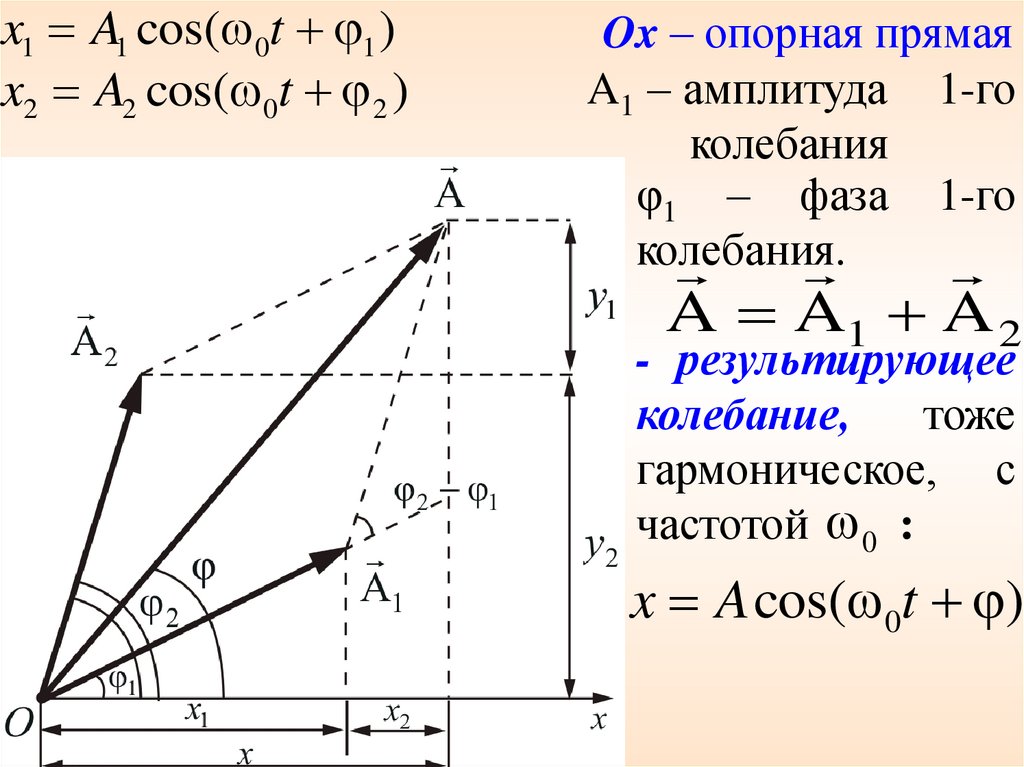
x1 A1 cos( 0t 1 )
x2 A2 cos( 0t 2 )
Ox – опорная прямая
A1 – амплитуда 1-го
колебания
φ1 – фаза 1-го
колебания.
A A1 A 2
- результирующее
колебание,
тоже
гармоническое, с
частотой 0 :
x A cos( 0t )

8.

По правилу сложения векторов найдем суммарную
амплитуду, результирующего колебания:
A A A 2 A1 A2 cos( 2 1 )
2
2
1
2
2
(2.2.2)
Начальная фаза определяется из соотношения
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2 cos 2
(2.2.3)
Амплитуда А результирующего колебания
зависит от разности начальных фаз 2 1

9.

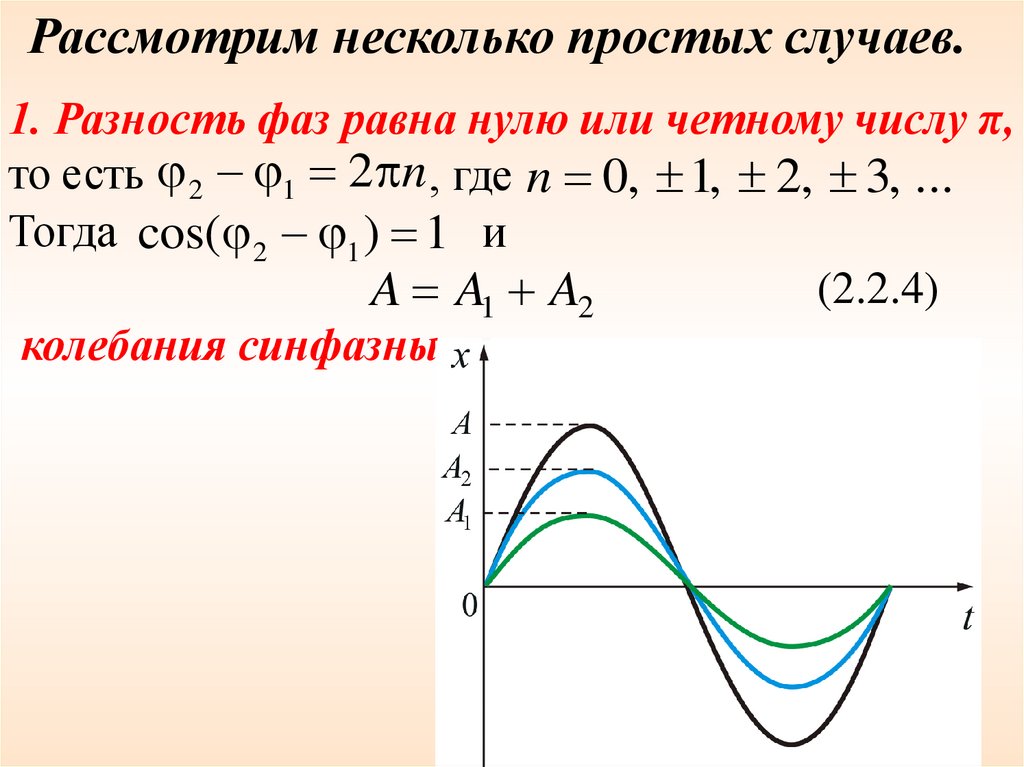
Рассмотрим несколько простых случаев.
1. Разность фаз равна нулю или четному числу π,
то есть 2 1 2 n , где n 0, 1, 2, 3, ...
Тогда cos( 2 1 ) 1 и
(2.2.4)
A A1 A2
колебания синфазны

10.

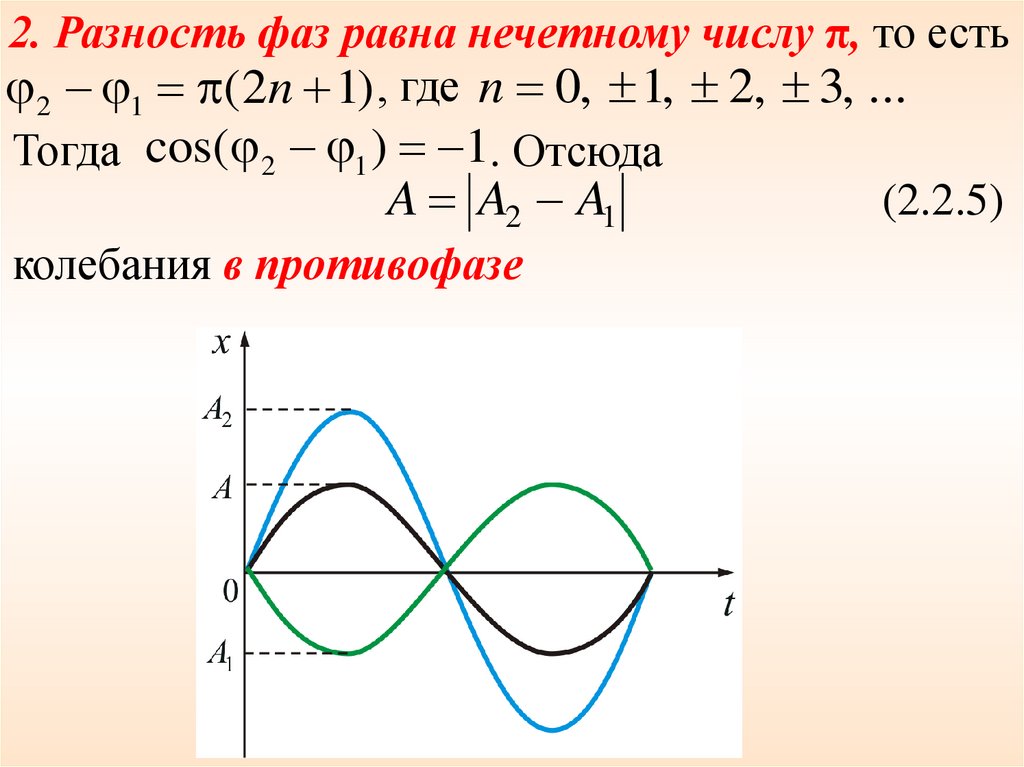
2. Разность фаз равна нечетному числу π, то есть
2 1 (2n 1) , где n 0, 1, 2, 3, ...
Тогда cos( 2 1 ) 1. Отсюда
(2.2.5)
A A2 A1
колебания в противофазе

11.

3. Разность фаз изменяется
произвольным образом
x1 A1 cos[ 1t 1 (t )]
x2 A2 cos 2t 2 (t )
во
времени
(2.2.6)
Это некогерентные колебания
Здесь интересен случай, называемый биениями,
когда частоты близки
1 2

12.

Периодические изменения амплитуды
колебания, возникающие при сложении двух
гармонических колебаний с близкими
частотами 1 2 , называются биениями.
x Aб cos 0t

13.

2.3. Сложение взаимно перпендикулярных колебаний СРС
x A1 cos( 0t 1 );
1 2 0
2
y A2 cos( 0 t 2 )
2 1
(2.3.1)
2
y
x
2 xy
2
2
cos( 2 1 ) sin ( 2 1 ) (2.3.2)
2
A2 A1 A1 A2
В результате
получили
уравнение эллипса
с произвольно
расположенными
осями

14.

15.

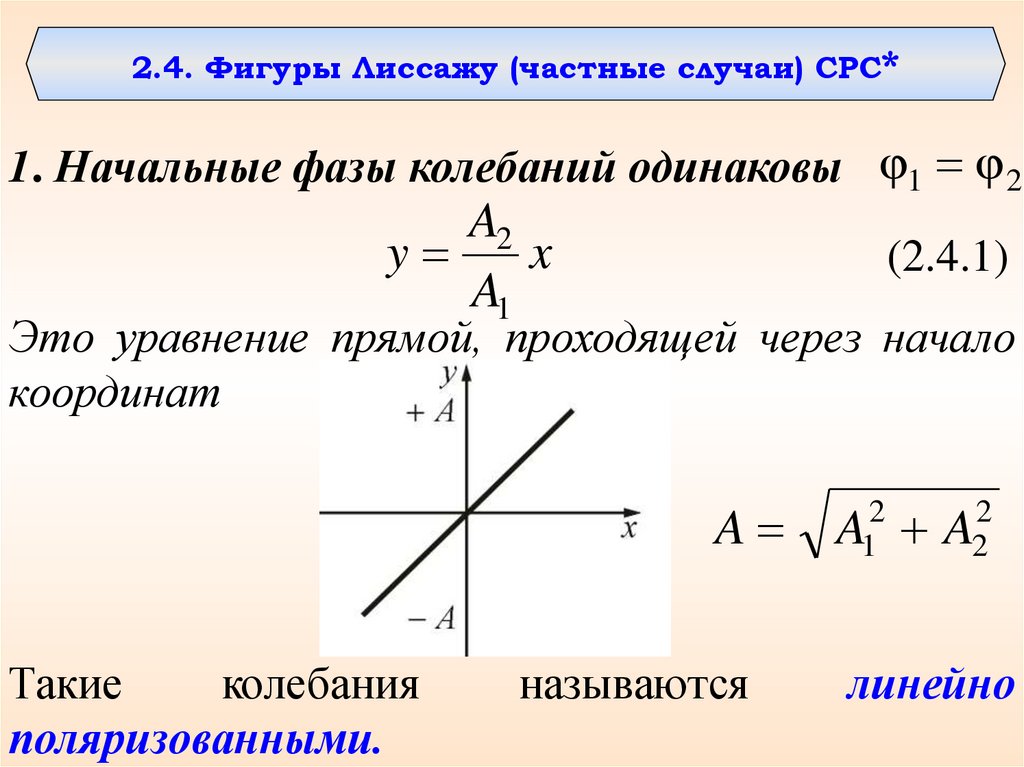
2.4. Фигуры Лиссажу (частные случаи) СРС*
1. Начальные фазы колебаний одинаковы φ1 φ 2
A2
y
x
A1
(2.4.1)
Это уравнение прямой, проходящей через начало
координат
A
Такие
колебания
поляризованными.
называются
2
2
A1 A2
линейно

16.

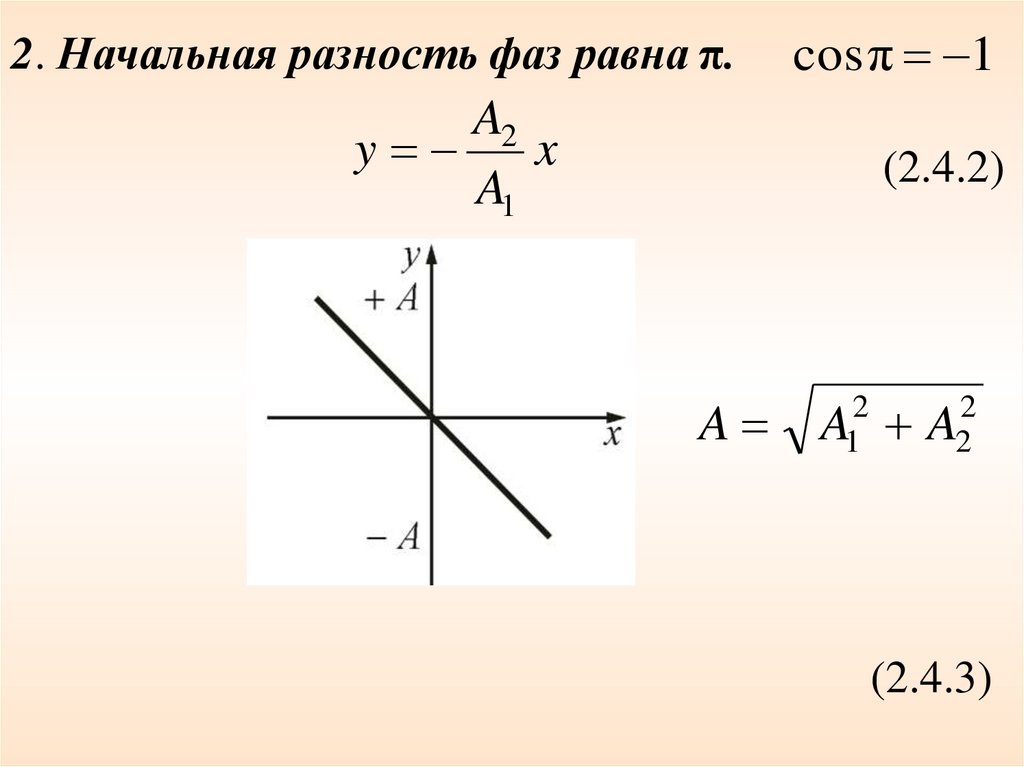
2. Начальная разность фаз равна π.
A2
y
x
A1
cos π 1
(2.4.2)
A
2
2
A1 A2
(2.4.3)

17.

3. Начальная разность фаз равна π/2. cos / 2 0
2
2
x
y
2 1
2
A1 A2
(2.4.4)
– это уравнение эллипса с полуосями А1 и А2
( Эллиптически поляризованные колебания)
При A1 A2 – получим уравнение окружности
(циркулярно-поляризованные колебания).

18.

4. Все остальные разности фаз дают эллипсы
с различным углом наклона относительно осей
координат.
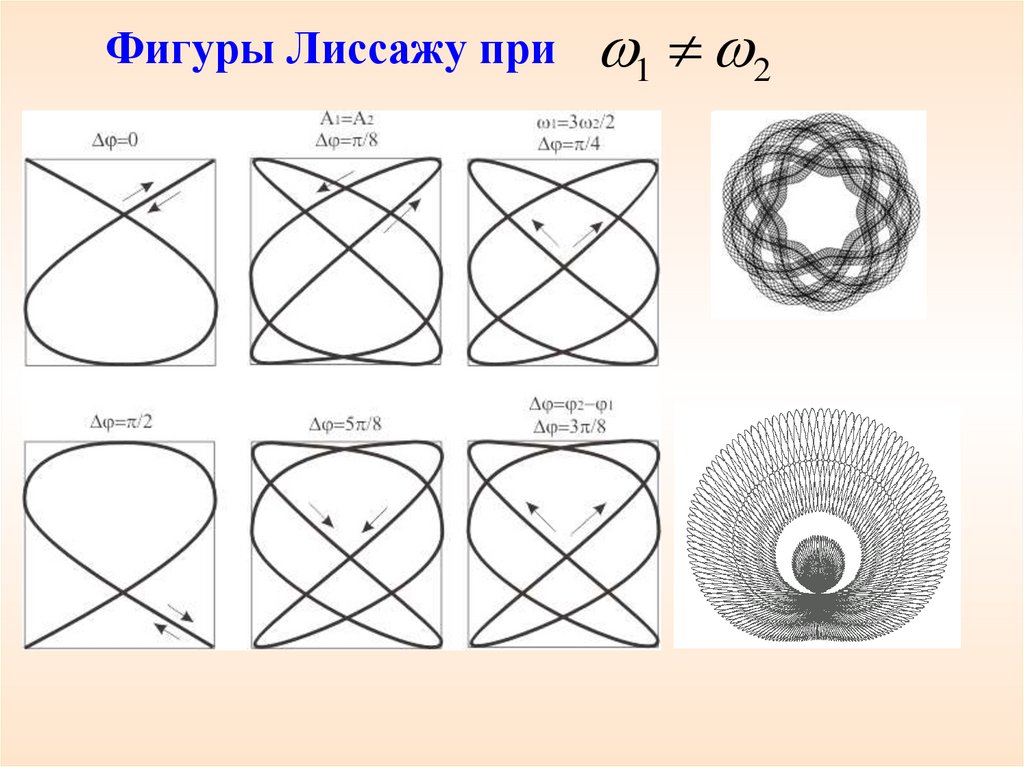
Фигуры, получаемые при сложении взаимно
перпендикулярных колебаний разных частот,
называются фигурами Лиссажу.
Здесь рассматривались простейшие случаи, когда
1 2 .
Если 1 2
тогда в результате будут
получаться уже не эллипсы, а более сложные
фигуры Лиссажу

19.

20.

Фигуры Лиссажу при
1 2

21.

22.

http://www.youtube.com/watch?v=DXpntnHxNZQ –
Фигуры Лиссажу. Видео.
http://arbuz.uz/w_lisagu.html – Фигуры Лиссажу:
первая любовь каждого программиста.
http://ligis.ru/effects/science/250/index.htm – Статья с
анимацией о фигурах Лиссажу.