Similar presentations:
Сложение колебаний. Затухающие колебания. Лекция № 2
1.
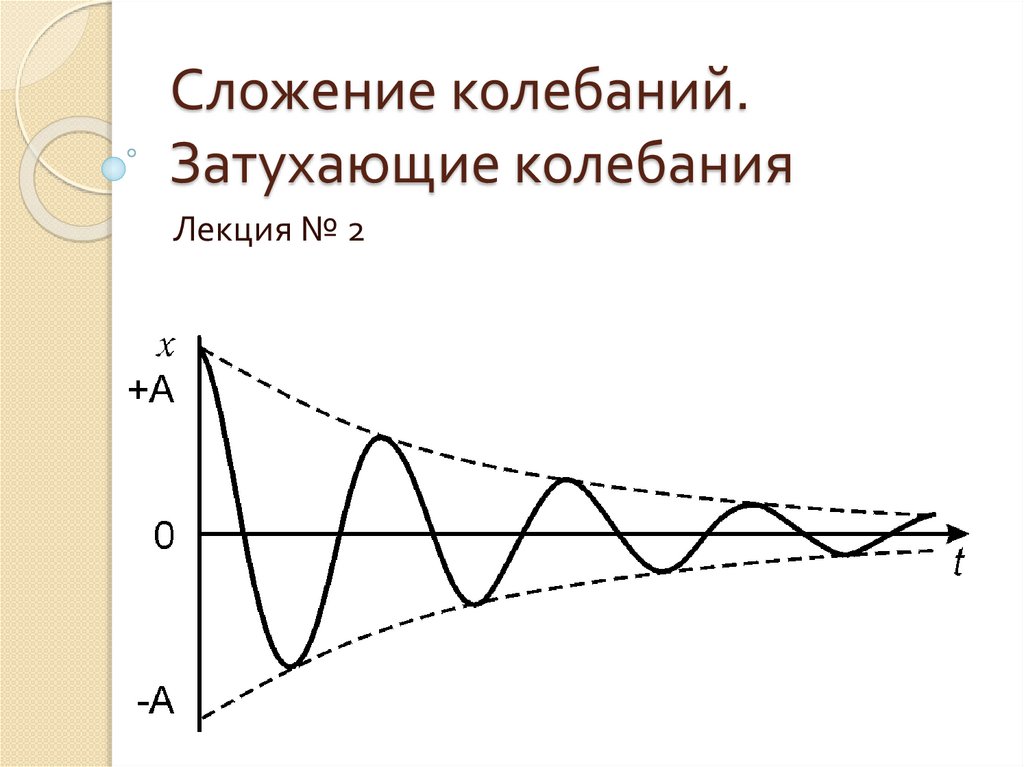
Сложение колебаний.Затухающие колебания
Лекция № 2
2.
План лекцииСложение гармонических
колебаний одного направления и
одинаковой частоты. Биения.
2. Сложение взаимно
перпендикулярных колебаний.
1.
3.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
Сложим гармонические колебания
одного направления и одинаковой
частоты:
x1 A1 cos 0t 1
x2 A2 cos 0t 2
4.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
Уравнение результирующего колебания
будет
x x1 x2 A cos 0t
где
2
A
2
2
A1 A2 2 A1 A2 cos 2 1
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2 cos 2
5.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
Проанализируем выражение для
амплитуды в зависимости от разности
фаз 2 1 :
1)
2 1 2m
(т=0, 1, 2, ...), тогда
A=A1+A2;
2) 2 1 2m 1 (т=0, 1, 2, ...), тогда
A=|A1–A2|.
6.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
Периодические изменения амплитуды
колебания, возникающие при сложении
двух гармонических колебаний с
близкими частотами, называются
биениями.
Пусть амплитуды складываемых
колебаний равны А, а частоты равны и
+ , причем << .
x1 A cos t ,
x2 A cos t .
7.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
Складывая эти выражения и учитывая, что
во втором сомножителе /2<< , найдем
x 2 A cos
t cos t
2
Амплитуда биений:
Aб 2 A cos
t
2
Частота биений:
б
Период биений:
2
Tб
8.
1. Сложение гармонических колебаний одногонаправления и одинаковой частоты. Биения
График биений:
9.
2. Сложение взаимноперпендикулярных колебаний
x A cos t ,
y B cos t
где ‒ разность фаз обоих колебаний,
А и В ‒ амплитуды складываемых
колебаний.
Исключаем параметр t:
x A cos t ;
y B cos t cos t cos sin t sin
10.
2. Сложение взаимноперпендикулярных колебаний
Заменяя во втором уравнении
cos t
sin t
x A
2
1 ( x / A)
Получаем уравнение эллипса:
x 2 2 xy
y2
2
cos 2 sin
2
A
AB
B
эллиптически поляризованные колебания
11.
2. Сложение взаимноперпендикулярных колебаний
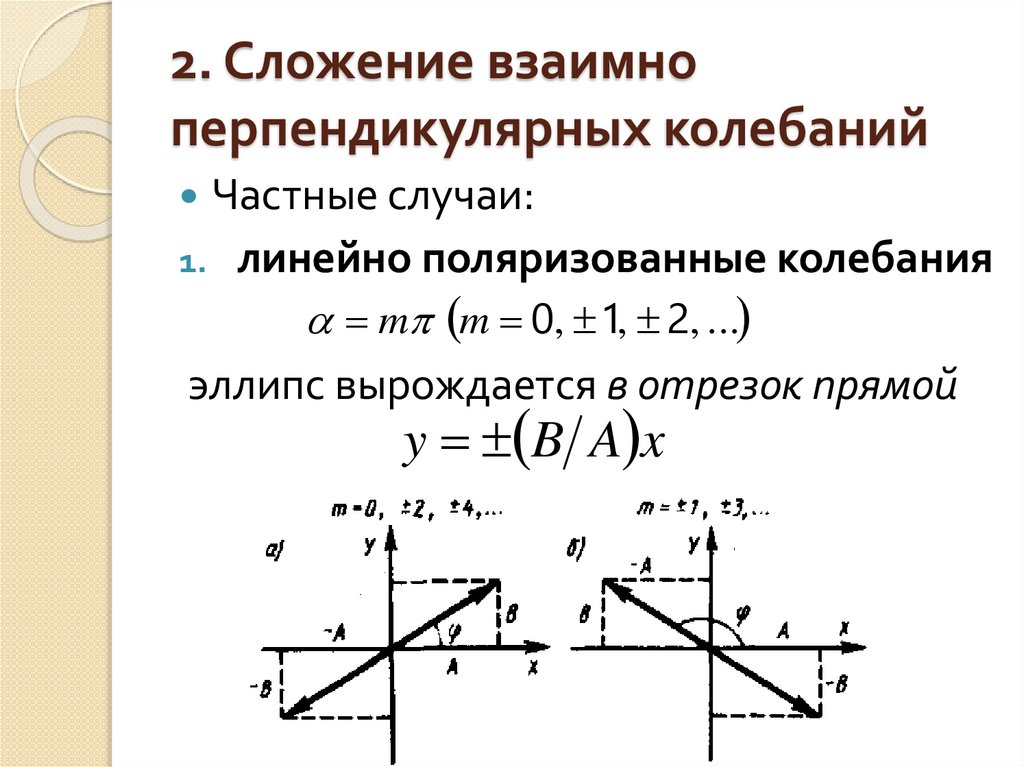
Частные случаи:
1.
линейно поляризованные колебания
m m 0, 1, 2, ...
эллипс вырождается в отрезок прямой
y B A x
12.
2. Сложение взаимноперпендикулярных колебаний
Результирующее колебание является
гармоническим колебанием с частотой
и амплитудой
A B
2
2
B
arctg cos m
A
13.
2. Сложение взаимноперпендикулярных колебаний
2.
эллиптически поляризованные
колебания
2m 1 m 0, 1, 2, ...
2
2
2
x
y
1
2
2
A B
14.
2. Сложение взаимноперпендикулярных колебаний
Если
A B
то эллипс вырождается в окружность.
Такие колебания называются
циркулярно поляризованными
колебаниями или колебаниями,
поляризованными по кругу.
15.
Дифференциальное уравнение свободныхзатухающих колебаний. Автоколебания
Затухающие колебания – колебания,
амплитуды которых из-за потерь энергии
реальной колебательной системой с
течением времени уменьшаются.
Дифференциальное уравнение
свободных затухающих колебаний:
d 2S
dS
2
2
0S 0
2
dt
dt
16.
Дифференциальное уравнение свободныхзатухающих колебаний. Автоколебания
Решение уравнения в случае малых затуханий
( 2 02 )
S A0e t cos t
где
A A0e
t
амплитуда затухающих
колебаний, а А0 начальная
амплитуда.
17.
Дифференциальное уравнение свободныхзатухающих колебаний. Автоколебания
Промежуток времени =1/ , в течение
которого амплитуда затухающих
колебаний уменьшается в е раз, называется
временем релаксации.
Период затухающих колебаний
T
2
2
02 2
Декремент затухания
A t
e T
A t T
18.
Дифференциальное уравнение свободныхзатухающих колебаний. Автоколебания
Логарифмический декремент затухания
A t
T
1
ln
T
A t T
Ne
Ne число колебаний, совершаемых за
время уменьшения амплитуды в е раз.
Добротность
Q
19.
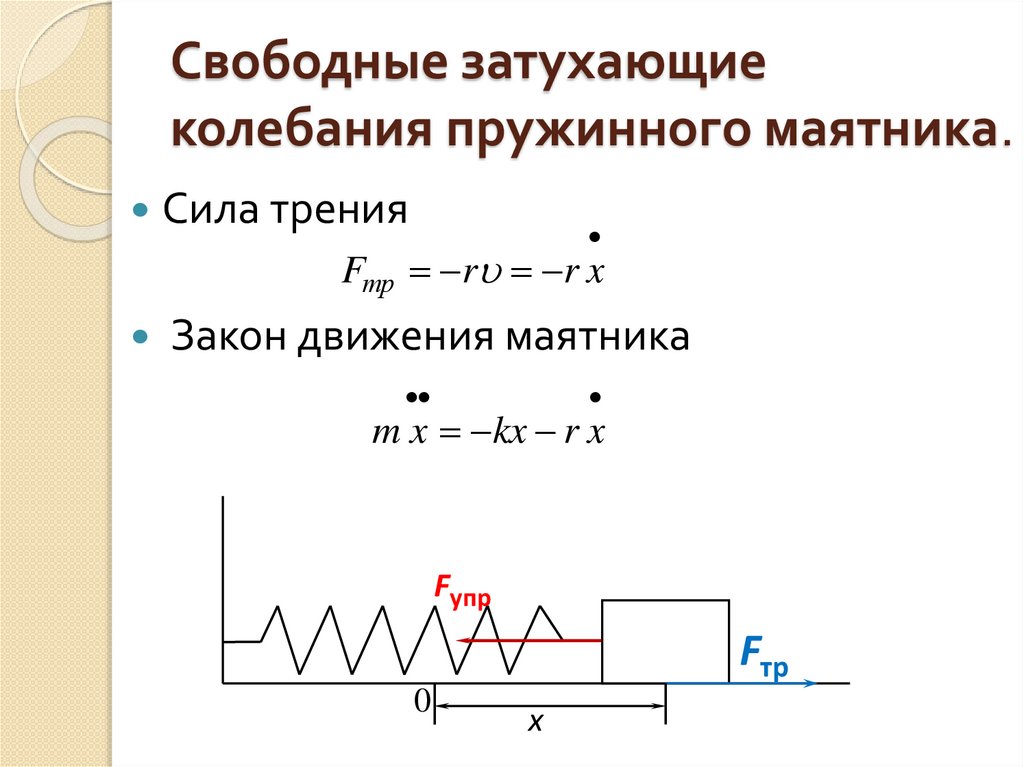
Свободные затухающиеколебания пружинного маятника.
Сила трения
Fтр r r x
Закон движения маятника
m x kx r x
Fупр
Fтр
0
x
20.
Свободные затухающие колебанияпружинного маятника
Используя формулу 0= k / m
и
принимая, что коэффициент затухания
r
2m
Получим дифференциальное
уравнение затухающих колебаний
маятника:
x 2 x 02 x 0
21.
Свободные затухающиеколебания пружинного маятника.
Решение уравнения:
x A0e t cos t
частота
2
r
02 2
4m
Добротность пружинного маятника:
Q= km /r.
22.
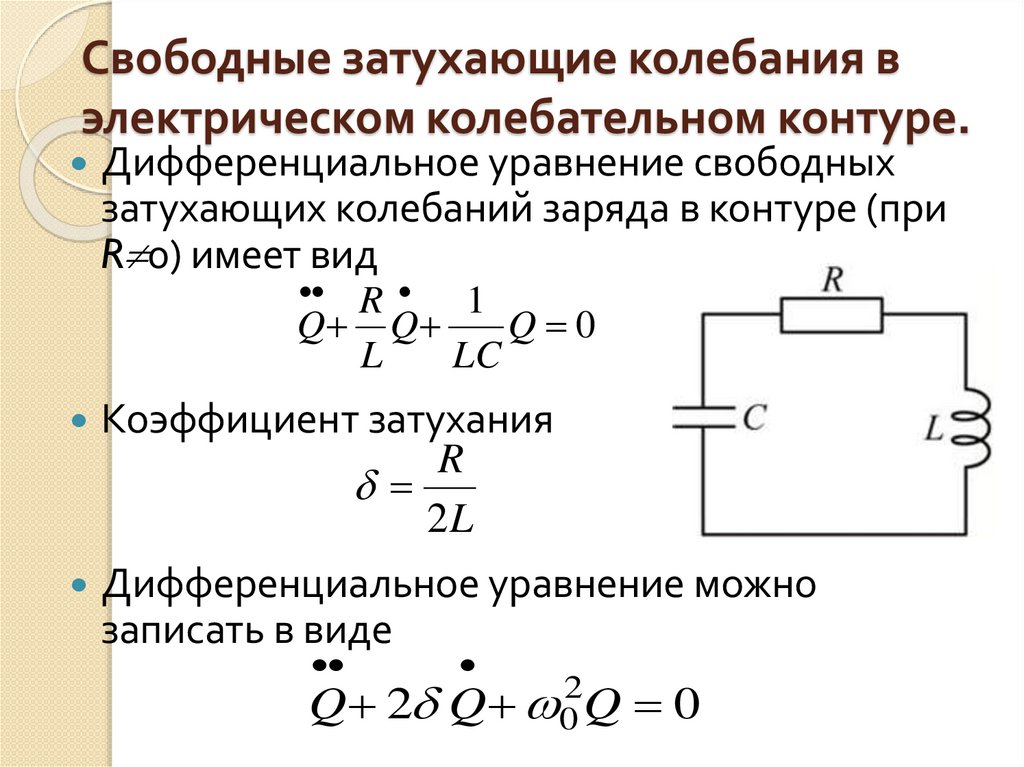
Свободные затухающие колебания вэлектрическом колебательном контуре.
Дифференциальное уравнение свободных
затухающих колебаний заряда в контуре (при
R 0) имеет вид
R 1
Q Q
Q 0
L
LC
Коэффициент затухания
R
2L
Дифференциальное уравнение можно
записать в виде
2
Q 2 Q 0 Q 0
23.
Свободные затухающие колебания вэлектрическом колебательном контуре.
Колебания заряда совершаются по закону
Q Qme
t
cos t
с частотой
1
R2
2
LC 4 L
Добротность колебательного контура
1 L
Q
R C
24.
Дифференциальное уравнение свободныхзатухающих колебаний. Автоколебания
Автоколебания незатухающие
колебания, поддерживаемые в
диссипативной системе за счет
постоянного внешнего источника энергии,
причем свойства этих колебаний
определяются самой системой.
Примером автоколебательной системы
могут служить часы.




















 physics
physics








