Similar presentations:
Гармонические колебания. Сложение гармонических колебаний
1.
General Physics NRNU MEPhIКолебательное движение.
Лекция 01
10 февраля 2021
Гармонические колебания.
Сложение гармонических колебаний.
Лектор: доцент НИЯУ МИФИ,
Андрей Станиславович ОЛЬЧАК
2.
Виды движения1. Поступательное движение
2. Вращательное движение
+Плоское движение = поступательное + вращение
3. Колебания (Oscillations)
3. Условия равновесия системы с одной степенью свободы.
Вблизи минимума любую гладкую функциюможно разложить в степенной ряд
Brook Taylor (1685-1731):
f(x) = f(x=0)+xf '(x=0)+(x2/2)f '' (x=0) + ...
… + (xn/n!)f (n)(x=0) +…
В системе координат с началом в точке минимума :
f(x=0) = 0; f '(x=0) = 0; f '' (x=0) > 0
f(x) ~= f’’(0)x2/2 = kx2/2
В механике минимуму потенциальной энергии соответствует положение
равновесия материальной точки или системы. ВОПРОС : какая сила будет
на материальную точку вблизи вблизи точки минимума ее потенциальной
энергии? ОТВЕТ:
Если U(x) = kx2/2, то F = -dU/dx = - kx
Такие силы называются квази-упругими, а коэффициент
квазиупругой силы.
k - коэффициент
4.
Движение под действием квазиупругойсилы
3-ой закон Ньютона):
mx’’(t) = F
F = - kx
mx’’(t) = - kx(t)
или
x’’(t) + ω02x(t) = 0,
где ω0 = (k/m)1/2 - круговая частота гармонических колебаний
Решение:
x(t)= A cos(ω0t + φ0)
x’(t)= -A ω0 sin(ω0t + φ0)
x’’(t)= - A ω02cos(ω0t + φ0).
4
5.
Гармонические колебанияЗависимость от времени
положения x(t)
x(t) = Acos(ωt + φ0)
скорости v(t)
vx(t) = - Aω sin(ωt + φ0)
ускорения w(t)
wx(t) = - Aω2cos(ωt + φ0) =
= - ω2x(t)
Ekin = px2(t)/2m = (m/2)A2ω2sin2(ωt + φ0) = (k/2)A2sin2 (ωt + φ0)
Epot = k x2(t)/2 = = (k/2)A2cos2 (ωt + φ0)
Ekin + Epot = E = (k/2)A2 = Const
5
6.
Гармонические колебанияx
T
A
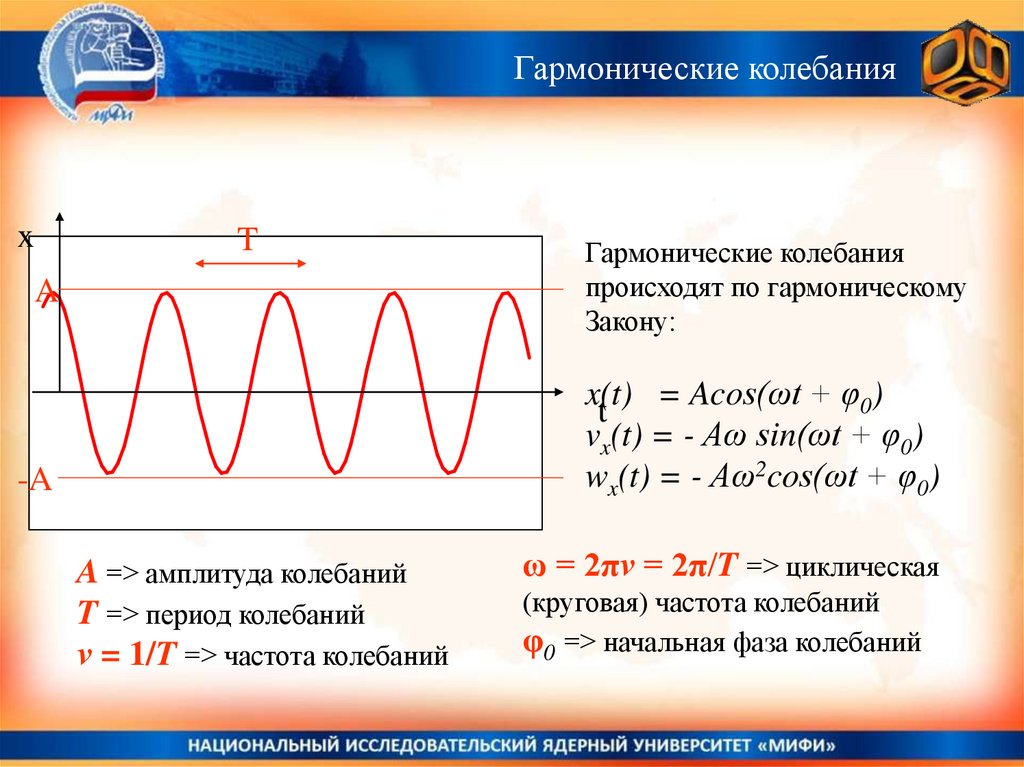
Гармонические колебания
происходят по гармоническому
Закону:
x(t)
t = Acos(ωt + φ0)
vx(t) = - Aω sin(ωt + φ0)
wx(t) = - Aω2cos(ωt + φ0)
-A
A => амплитуда колебаний
T => период колебаний
ν = 1/T => частота колебаний
ω = 2πν = 2π/T => циклическая
(круговая) частота колебаний
φ0 => начальная фаза колебаний
7.
Пример: Пружинный маятникГоризонтальный пружинный маятник движется под
действием упругой силы (закон Гука)):
Fупр = - kx(t)
Уравнение движения пружинного маятника
X=0
Fупр = - kX
X(t)
X
mx’’(t) = - kx(t)
или
x’’(t) + ω02x(t) = 0,
где ω0 = (k/m)1/2 - круговая частота
гармонических колебаний
Решение:
x(t)= A cos(ω0t + φ0)
x’(t)= -A ω0 sin(ω0t + φ0)
x’’(t)= - A ω02cos(ω0t + φ0).
7
8.
ПРИМЕР 2: Математический маятникL
φ(t)
Если угол отклонения маятника невелик
(φ << 1 рад), то sin(φ) ~= φ и второй закон
Ньютона в проекции на ось Х можно записать в
mwt = - mgφ
виде:
mg sin(φ)
mg
Тангенциальное ускорение выражается через
Х угловое ускорение:
wt = Lφ’’(t)
В результате для угла отклонения φ(t) получаем уравнение гармонических
колебаний:
φ’’(t) + ω02φ(t)
Причем ω02
= g/L
8
9.
ПРИМЕР 3: Физическиймаятник
o
L
C
m
Физический маятник - массивное тело, совершающее
(небольшие) колебания на оси подвеса
L - расстояние от центра масс до точки подвеса маятника
Полная механическая энергия физ. маятника всегда равна:
E = T+U =Izω2/2+mgL(1-cosφ)
При небольших углах отклонения φ<<1 рад
1-cosφ ~= φ2/2;
U = mgLφ2/2
dE/dt=0 => Izφ’’(t) + mgLφ(t) = 0
=> φ’’(t) + (mgL/ Iz)φ(t) = 0
Маятник совершает гармонические колебания с круговой частотой
ω0 = (mgL/ Iz)1/2
9
10.
Уравнение гармонических колебанийУравнение гармонических колебаний
x’’(t) + ω02x(t) = 0 выводится
из второго закона Ньютона для ЛЮБОЙ системы, движущейся под действием
квазиупругой силы F
= -kx(t), где коэффициент пропорциональности k
зависит от природы системы, ω02 = k/m
Уравнение гармонических колебаний
x’’(t) + ω02x(t) = 0 возникает
ВСЕГДА, когда материальная точка движется в поле с потенциальной энергией,
= kx2/2.
ω02 = k/m
параболически зависящей от отклонения от положения равновесия: U
Коэффициент k зависит от природы потенциального поля сил.
11. Гармонические колебания
Уравнение гармонических колебаний:x’’(t) + ω02x(t) = 0
Общее решение этого уравнения:
x(t) = Acos(ω0 t + φ0),
А - амплитуда колебаний и φ0 - начальная фаза колебаний
(определяются из начальных условий задачи).
Энергия гармонических колебаний:
T = mV2/2 = mA2ω02 sin2(ω0 t + φ0)/2
U = kx2/2 = kA2cos2(ω0 t + φ0)/2
E = mA2ω02/2 =mVmax2/2 = kA2/2 = Const
11
12.
Сложение гармонических колебанийИтак - общий закон гармонических колебаний
x(t) = Acos(ω0 t + φ0),
где А - амплитуда колебаний и φ0 - начальная фаза колебаний
Представим себе, что одно и то же тело может совершать колебательное
движение под действием 2 или более разных причин с 2-мя или более
разными частотами и амплитудами:
x1(t) = A1cos(ω1t + φ1), x2(t) = A2cos(ω2 t + φ2), …
Наложение даже 2-х мод гармонических колебаний с разными частотами
может дать весьма сложную и негармоническую картину движения
x(t) = A1cos(ω1t + φ1) + A2cos(ω2 t + φ2) +
ВАЖНО! Иногда даже очень сложную функцию можно представить в виде
суммы небольшого числа гармонических колебаний!
12
13.
Гироскопические эффекты.x(t) = А0+A1cos(ω1t + φ1)+A2cos(ω2t + φ2)+A3cos(ω3t + φ3)
Периоды (для Земли):
1) прецессия – 25,8 тыс. лет
2) нутация – 41 тыс.лет
3) изменение эксцентрисета – 92 тыс.лет
Слободан Миланкович, 1939
14.
Сложение гармонических колебанийИнтересный случай – сложение двух колебаний с одинаковыми (близкими)
амплитудами и близкими (но НЕ одинаковыми) частотами:
x(t) = Acos(ωt) + Acos(ωt+Δωt) =
= 2Acos(Δωt/2)cos(ωt + Δωt/2) ~=
= 2Acos(Δωt/2)cos(ωt) = A(t)cos(ωt)
Гармонические
колебания с
периодически
меняющейся
амплитудой –
биения.
14
15.
Сложение гармонических колебанийСложение двух колебаний в разных плоскостях:
x (t) = A1cos(ω1t + φ1), y (t) = A2cos(ω2 t + φ2)
.
- сложение таких колебаний может давать как картину полного хаоса, так
и (при некоторых условиях) красивую «гармоничную» картину
регулярного движения.
15
16.
Сложение гармонических колебанийСложение двух колебаний в разных плоскостях:
x (t) = A1cos(ω1t + φ1), y (t) = A2cos(ω2 t + φ2)
.
ПРИМЕР 1: ω1
= ω 2 ; φ1 = φ2 .
y
A2
y (t) = (A2 /A1)x (t) =>
x
.
A1
16
17.
Сложение гармонических колебанийСложение двух колебаний в разных плоскостях:
x (t) = A1cos(ω1t + φ1), y (t) = A2cos(ω2 t + φ2)
.
ПРИМЕР 2: ω1
= ω2 ; φ2 = φ1 + π/2.
.
x(t) = A1cos(ωt + φ0),
y(t) = +A2sin(ωt + φ0),
y
A2
x
A1
17
18.
Сложение гармонических колебанийСвязь колебательного и вращательного движения
Пример 3:
ω
φ0 + ωt
R
φ0
φ = φ0 + ωt
x(t) = R cos(ωt + φ0),
y(t) = R sin(ωt + φ0),
19.
Сложение гармонических колебанийСложение двух колебаний с кратными частотами, но в разных плоскостях:
x1(t) = A1cos(ω1t + φ1), y2(t) = A2cos(ω2 t + φ2)
Если ω1 / ω2 = n/m, где n, m = 1, 2, 3, 4… - целые числа.
- сложение таких колебаний дает очень красивую «гармоничную»
картину движения (фигуры Лиссажу)
19
20.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
21.
КолебанияЗатухающие колебания
21
22. Уравнение колебаний
Рассмотрим движение системы вблизи положения равновесия поддействием квазиупругой силы (гармонические колебания), но
с учетом возможного действия других сторонних сил.
Таким движениям соответствует уравнение:
mx’’(t) = - kx(t) + F(x,x’,t)
или:
где
x’’(t) + ω02x(t) = F(x,x’,t)/m
ω02 = k/m
22
23. Затухающие колебания
x’’(t) + ω02x(t) = F(x,x’,t)/mЕсли сторонняя сила – это сила сопротивления среды,
x’’(t) + ω02x(t) = - (r/m)x’(t)
Введем обозначение r/m = 2β. Величина β называется
F = -rx’(t):
коэффициентом затухания и имеет размерность [1/с],
совпадающую с размерностью циклической частоты.
x’’(t) + 2βx’(t) + ω02x(t) = 0
Решение этого дифференциального уравнения будет содержать не только
синусы (или косинусы), но и экспоненту!
Нам необходимо вспомнить немного математики!
23
24. Немного математики! Функции комплексных переменных.
Синусы, косинусы и экспоненты на поле функций комплексныхпеременных представляются в общем виде (формула Эйлера):
Если Z
= a+ib - комплексное число (где i = (-1)1/2 -мнимая
единица), то экспонента от этого числа представляется в виде:
exp(Z)=exp(a+ib) = exp(a)(cos(b) + i sin(b))
Будем искать решение нашего уравнения
x’’(t) + 2βx’(t) + ω2x(t) = 0
в виде
x(t) = А0 exp(Zt+iφ0), где Z = a+iω
а затем возьмем от него действительную часть, соответствующую
физической постановке задачи.
24
25.
Затухающие колебанияИтак, ищем решение уравнения
в виде
x’’(t) + 2βx’(t)+ ω02x(t) = 0
x(t) = А0 exp(Zt+iφ0); Z = a+iω
Подставим предполагаемое решение в уравнение:
А0 Z2exp(Zt+iφ0) + +2βА0Zexp(Zt +iφ0) +
+ ω02А0exp(Zt+iφ0)=0
=>
Z2+2βZ + ω02 =0 => (a+iω)2+2β(a+iω)+ω02=0
=> a2+i2aω - ω2 +2βa+i2βω +ω02=0
Приравняем нулю отдельно действительную и мнимую часть уравнения:
a2 - ω2 +2βa+ω02=0;
2aω + 2βω = 2ω(a + β) = 0 => a = - β
25
26.
Затухающие колебанияИтак, мы ищем решение уравнения
в виде
x’’(t) + 2βx’(t)+ ω02x(t) = 0
x(t) = А0 exp(Zt+iφ0);
Нашли:
Z = a+iω
a2 - ω2 +2βa+ω02=0; причем a = -β =>
β2 - ω2 - 2β2 +ω02=0; => ω2 = ω02 - β2
По формуле Эйлера искомое решение имеет вид:
x(t) = А0 exp(-βt)(cos(ωt +φ0)+i sin(ωt +φ0))
Физический смысл имеет действительная часть решения (при ω0 >β):
x(t) = А0 exp(-βt)(cos(ωt +φ0)),
А0 – начальная амплитуда, φ0 - начальная фаза, ω = (ω02 - β2)1/2 -
где
круговая частота колебаний
26
27.
Затухающие колебанияИтак, решение нашего уравнения
x’’(t) + 2βx’(t)+ ω02x(t) = 0
при ω0 >β имеет вид: x(t) = А(t)(cos(ωt +φ0))
И соответствует гармоническим колебаниям с круговой частотой
ω = (ω02 - β2)1/2 и с экспоненциально затухающей амплитудой
А(t)=А0exp(-βt).
Важные характеристики затухающих колебаний:
T = 2π/ω = 2π/(ω02 - β2)1/2
Декремент (decrement) затухания exp(βT) = A(t)/A(t+T)
Логарифмический декремент затухания λ= βT.
Добротность (Q-factor) Q = π/λ = ω/2β = (ω02 - β2)1/2 /2β
- “Период” (period) колебаний
-
27
28.
Затухающие колебанияСвободные затухающие колебания.
28
29.
Апериодическое движениеОсобый интерес представляет случай ω0 < β, когда ω = (ω02 - β2)1/2 мнимое число. В этом случае общее решение уравнения можно переписать в
виде
x(t) = А0exp(-βt - (β2 - ω02)1/2 t + iφ0)
Физический смысл имеет действительная часть решения:
x(t) = А0cos(φ0) exp(-(β +(β2 - ω02)1/2)t),
что соответствует экспоненциально затухающему движению. Это случай очень
большой силы трения. Исчезает физический смысл фазы движения.
Если коэффициент затухания много больше собственной частоты, то движение
системы перестает зависеть и от собственной частоты системы
x(t) =~ Аexp(-2βt)
29
30.
Курс общей физики НИЯУ МИФИСпасибо за внимание!





























 physics
physics








