Метод векторной диаграммы. Сложение гармонических колебаний. Биения

1.

Кафедра физики
ЛЕКЦИЯ 8
ПЛАН ЛЕКЦИИ
1. Метод векторной диаграммы. Сложение
гармонических колебаний. Биения.
2. Сложение
взаимно
перпендикулярных
колебаний. Фигуры Лиссажу.
3. Свободные затухающие колебания.
Общая физика. «Физика колебаний и волн»
1

2.

Кафедра физики
Метод векторной диаграммы
Графическое изображение колебаний в виде векторов на плоскости векторная диаграмма.
Рассмотрим произвольный вектор a, образующий с осью x угол .
Пусть вектор вращается относительно точки О с угловой скоростью 0.
Проекция конца вектора будет перемещаться по оси в пределах от +А
до -А.
0
Закон изменения координаты
проекции со временем:
a
O
x
x A cos 0 t
x
Общая физика. «Физика колебаний и волн»
2

3.

Кафедра физики
Метод векторной диаграммы
0
O
a
x
x
Проекция конца вектора a будет совершать
гармоническое колебание с амплитудой,
равной длине вектора, с круговой частотой,
равной угловой скорости 0 вращения
вектора, и с начальной фазой, равной .
x A cos 0 t
Гармоническое колебание может быть задано с помощью вектора,
длина которого равна амплитуде колебания, а направление вектора
образует с осью х угол, равный начальной фазе колебания.
Общая физика. «Физика колебаний и волн»
3

4.

Кафедра физики
Сложение гармонических колебаний.
Сложим два гармонических колебания одинакового направления и
одинаковой частоты:
x1 A1 cos 0 t 1
и
x 2 A2 cos 0 t 2
В любой момент времени смещение x колеблющейся точки будет
суммой смещений x 1 и x 2 .
Определим вид и параметры результирующего
Воспользуемся методом векторной диаграммы.
колебания.
Каждое
из колебаний в отдельности представляет собой вектор ( a1 и
.a ),
длина которого равна амплитуде колебания, а направление вектора
2
образует с осью
угол, равный
начальной фазе колебания.
x
Общая физика. «Физика колебаний и волн»
4

5.

Кафедра физики
Сложение гармонических колебаний.
a
a1
O
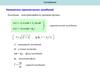
Проекция этого вектора на ось x равна
сумме проекций слагаемых векторов:
2
0
1
По правилам сложения векторов
построим результирующий вектор a .
a2
x2
x1
x
x x1 x 2
x
Результирующий вектор вращается с
той же угловой
скоростью 0 , что и
векторы a 1 и a 2 .
Следовательно, результирующее колебание будет гармоническим
колебанием с частотой 0 , амплитудой A и начальной фазой 0:
x A cos 0 t 0
Общая физика. «Физика колебаний и волн»
5

6.

Кафедра физики
Сложение гармонических колебаний.
x A cos 0 t 0
O
A2 A12 A22 2 A1 A2 cos 2 1
a
a1
1
В этом уравнении
2
0
x2
a2
x1
x
A1 sin 1 A2 sin 2
tg 0
A1cos 1 A2 cos 2
x
Вывод: метод векторной диаграммы
позволяет свести сложение нескольких
гармонических колебаний одной частоты
к операции сложения векторов.
Из анализа выражения для амплитуды:
а) Если разность фаз колебаний 2 1 равна или кратна
нечетному числу , (колебания находятся в противофазе), то
амплитуда результирующего колебания равна по модулю разности
амплитуд A2 A1 . Колебания максимально ослабляют друг друга.
Общая физика. «Физика колебаний и волн»
6

7.

Кафедра физики
Сложение гармонических колебаний.
x A cos 0 t 0
a
a1
1
O
A2 A12 A22 2 A1 A2 cos 2 1
2
0
x2
a2
x1
x
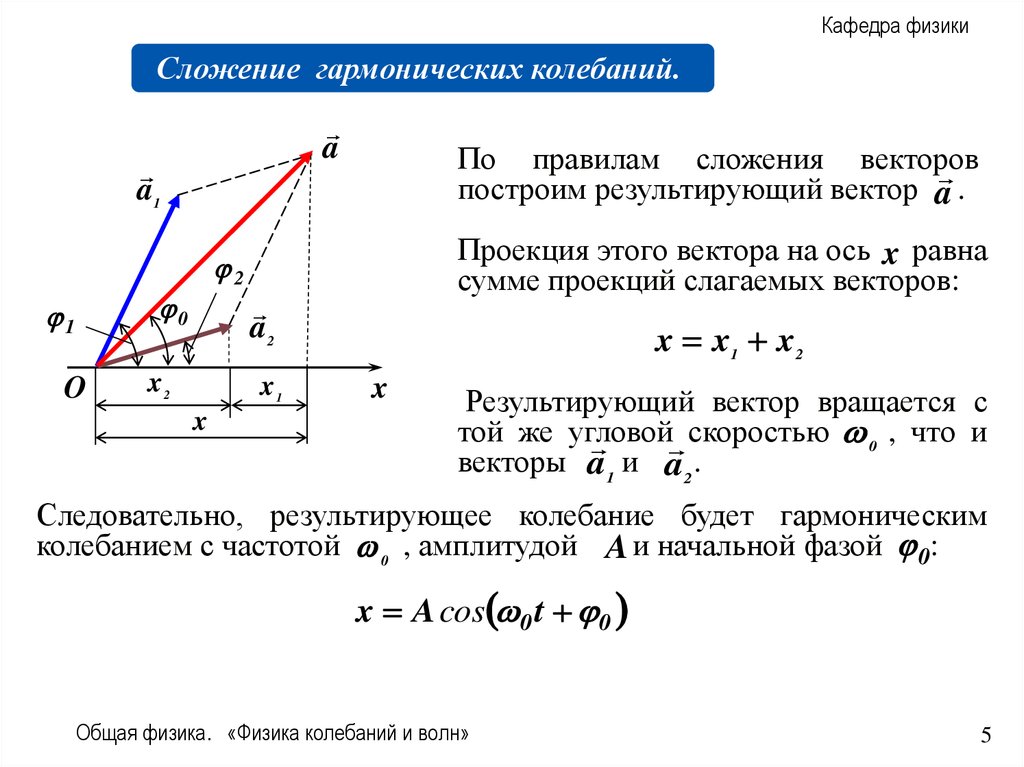
б) Если частоты
колебаний различны, то
векторы a 1 и a 2 будут вращаться с разными
угловыми
скоростями
на
векторной
диаграмме.
x
Результирующий вектор в этом случае уже
не будет определять гармоническое
колебание. Его величина и скорость
вращения будут меняться со временем.
Квадрат результирующей амплитуды
выражаться уравнением вида
такого
колебания
будет
A2 A12 A22 2 A1 A2 cos 2 1 t
Сумма гармонических колебаний одного направления с разными
частотами не является гармоническим колебанием.
Общая физика. «Физика колебаний и волн»
7

8.

Кафедра физики
Сложение гармонических колебаний.
a
Пусть два складываемых гармонических
a1
колебания одинакового направления мало
2
различаются по частоте. Результирующее
0
движение - гармоническое колебание с
a2
пульсирующей амплитудой - биения.
1
O
x2
x1
x
x
Биения
Имеются два колебания, различающиеся только частотами:
x1 A cos t ,
x2 A cos t ,
Результат сложения колебаний:
x 2 A cos
t cos t
2
Итог: получили выражение для почти гармонического колебания с
частотой . Амплитуда изменяется по периодическому закону.
Aбиений 2 A cos
t
2
- циклическая частота биений
Tбиений 2 - период биений.
Общая физика. «Физика колебаний и волн»
8

9.

Кафедра физики
Сложение гармонических колебаний.
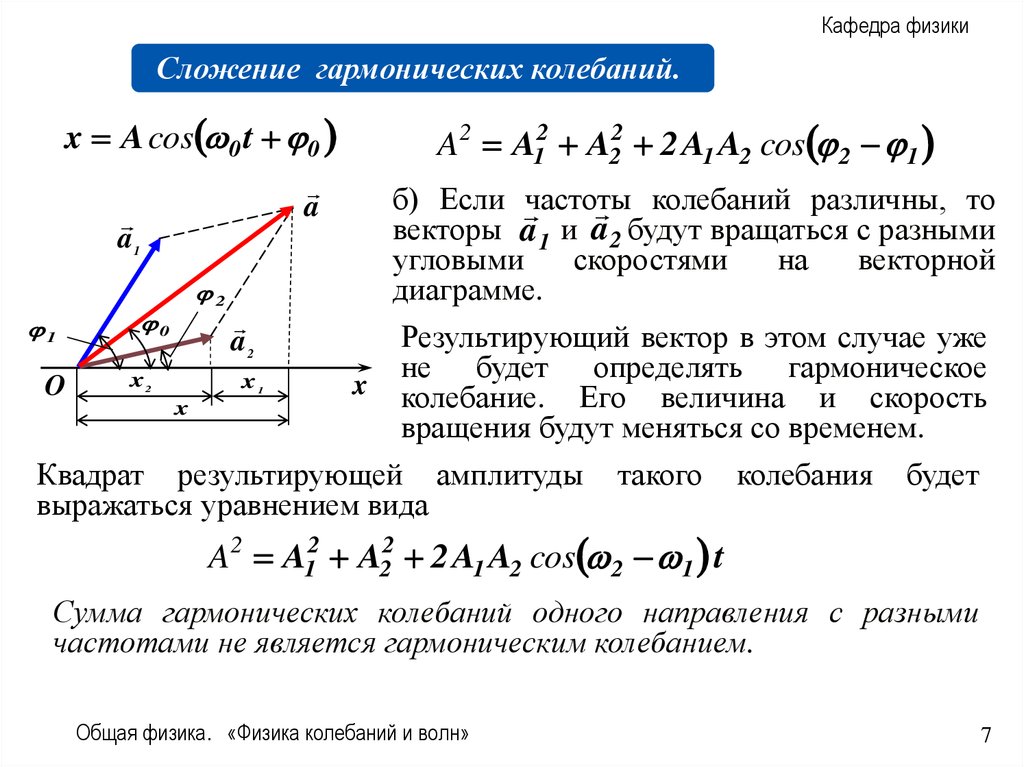
Биения
x
T 2
x 2 A cos
t cos t
2
Амплитуда
t
Aбиений 2 A cos
t
2
Tбиений 2
Общая физика. «Физика колебаний и волн»
t
Tбиений 2
9

10.

Кафедра физики
Сложение гармонических колебаний.
Сложение взаимно перпендикулярных колебаний.
Рассмотрены варианты сложения однонаправленных колебаний.
Сложение разнонаправленных колебаний - более сложный случай.
Рассмотрим результат сложения двух гармонических колебаний
одинаковой частоты, происходящих во взаимно перпендикулярных
направлениях вдоль осей x и y .
Пример: на управляющие вертикальные и горизонтальные пластины
осциллографа поданы периодические гармонические сигналы.
Пусть начальная фаза первого колебания равна нулю. Уравнения
колебаний:
x A cos t
y B cos t
Общая физика. «Физика колебаний и волн»
10

11.

Кафедра физики
Сложение гармонических колебаний.
Сложение взаимно перпендикулярных колебаний.
Для
нахождения
уравнения
траектории
x A cos t
результирующего колебания из уравнений
y B cos t
исключается t.
После преобразований:
x 2 y 2 2 xy
2
cos
sin
2
2
AB
A
B
Анализ:
а) Пусть разность фаз n , n 0 , 1, 2 , .... Из уравнения следует
x2 y2
n 2 xy
2 1
0
2
AB
2
A
B
x 2 y 2 2 xy x y
При четных n получается
2
0,
2
AB A B
A
B
B
x y
или
0 , y x
A
A B
B
При нечетных n получается y x
A
Общая физика. «Физика колебаний и волн»
11

12.

Кафедра физики
Сложение гармонических колебаний.
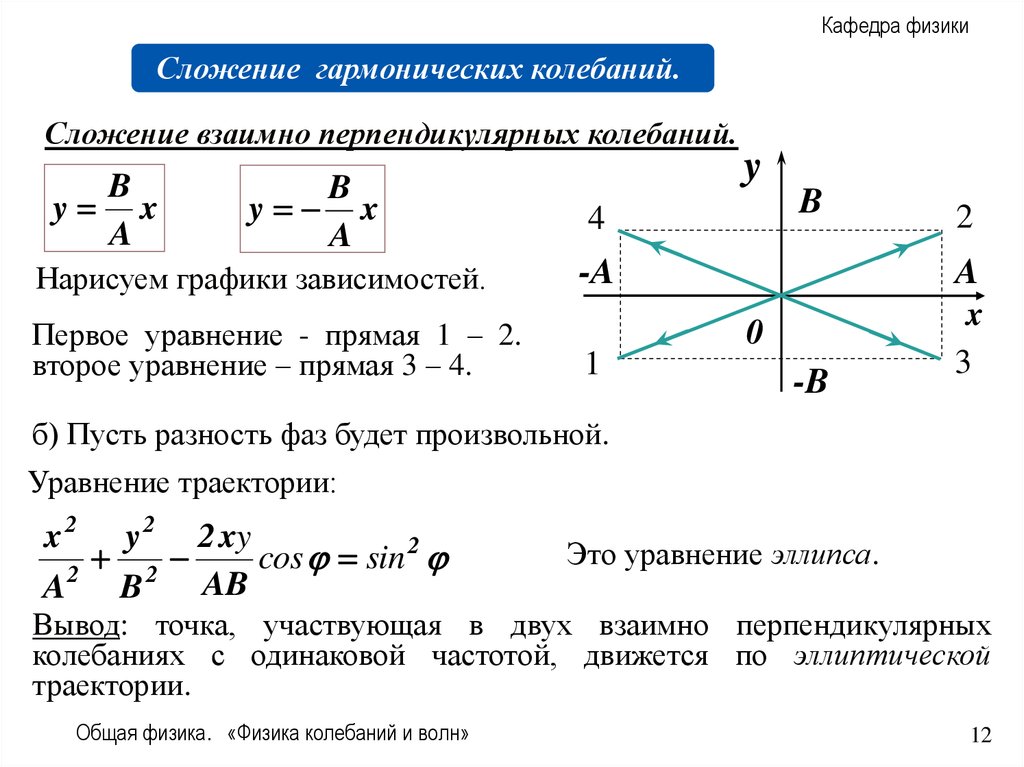
Сложение взаимно перпендикулярных колебаний.
B
y x
A
y
B
x
A
Нарисуем графики зависимостей.
Первое уравнение - прямая 1 – 2.
второе уравнение – прямая 3 – 4.
y
4
B
-A
1
2
A
0
-B
x
3
б) Пусть разность фаз будет произвольной.
Уравнение траектории:
x 2 y 2 2 xy
2
cos
sin
2
2
AB
A
B
Это уравнение эллипса.
Вывод: точка, участвующая в двух взаимно перпендикулярных
колебаниях с одинаковой частотой, движется по эллиптической
траектории.
Общая физика. «Физика колебаний и волн»
12

13.

Кафедра физики
Сложение гармонических колебаний.
Сложение взаимно перпендикулярных колебаний.
Параметры траектории определяются соотношением амплитуд и
разностью фаз исходных колебаний.
Пример: если 1 2 n , n 1, 2 , .... , то получим уравнение
2
вида
y
B 2 .
2
2
x
y
Это каноническое
1
уравнение эллипса -A
A
A2 B 2
Стрелки показывают направление
движения точки вдоль траектории
при 2 и 2 .
0
x
-B 2
Полуоси эллипса равны соответствующим амплитудам колебаний.
При A B эллипс вырождается в окружность.
Общая физика. «Физика колебаний и волн»
13

14.

Кафедра физики
Сложение гармонических колебаний.
Сложение взаимно перпендикулярных колебаний.
Если частоты взаимно перпендикулярных колебаний неодинаковы, то
траектория результирующего движения может иметь вид сложных
кривых, называемых фигурами Лиссажу.
Пример: Пусть отношение частот взаимно перпендикулярных
колебаний равно 1:2 и разность фаз 2 .
Уравнения колебаний имеют вид:
x A cos t , y B cos 2 t
2
Результирующее колебание показано на
рисунке.
Траектория вырождается в незамкнутую
кривую, по которой точка движется туда и
обратно. Это одна из простейших фигур
Лиссажу.
Общая физика. «Физика колебаний и волн»
y
B
-A
0
A
x
-B
14

15.

Кафедра физики
Свободные затухающие колебания.
В реальных системах всегда присутствуют процессы, приводящие к
диссипации энергии. Это, например, силы трения. Происходит
затухание (изменение амплитуды) колебаний.
Рассмотрим законы изменения параметров свободных затухающих
колебаний.
Свободные затухающие колебания – это такие свободные колебания,
амплитуда которых из-за потерь энергии реальной колебательной
системой с течением времени уменьшается.
Закон затухания колебаний определяется свойствами колебательных
систем.
Общая физика. «Физика колебаний и волн»

16.

Кафедра физики
Свободные затухающие колебания.
Дифференциальное уравнение свободных затухающих колебаний:
d2x
dx
2
2
0x 0
2
dt
dt
const - коэффициент затухания
0 -
собственная частота колебательной системы (частота
свободных незатухающих колебаний в отсутствие потерь энергии).
В случае малых затуханий ( 0 ) решение уравнения затухающих
колебаний имеет вид
х A0 e t cos t
Общая физика. «Физика колебаний и волн»

17.

Кафедра физики
Свободные затухающие колебания.
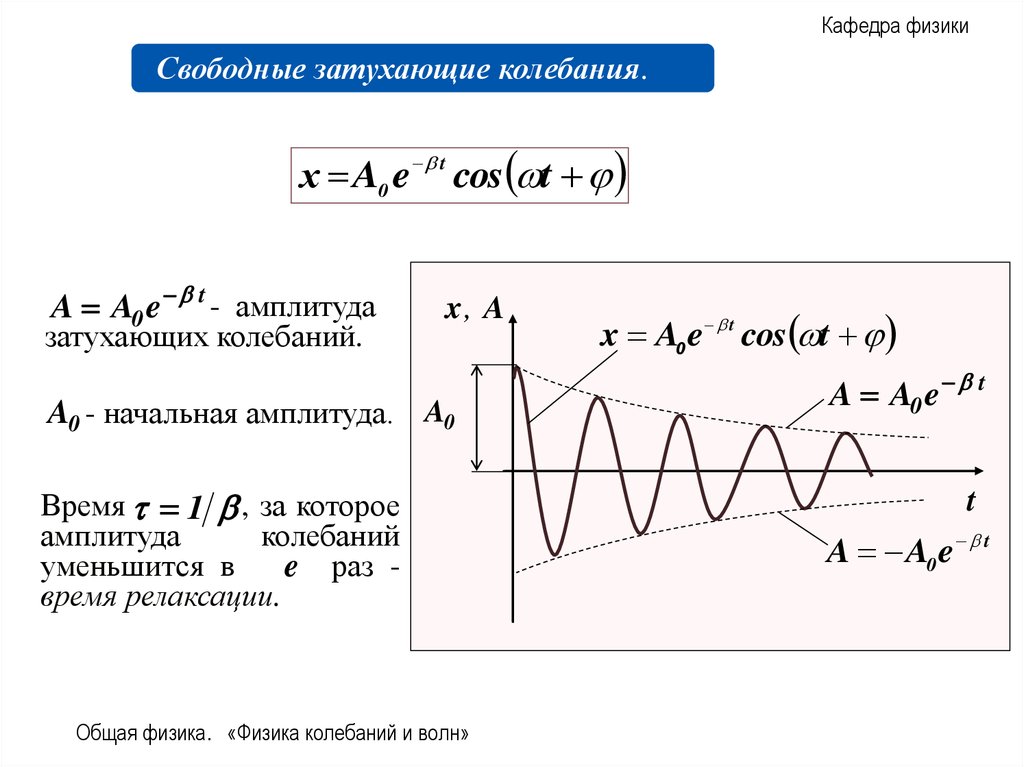
х A0 e t cos t
A A0 e t - амплитуда
затухающих колебаний.
x, A
A0 - начальная амплитуда. A0
Время 1 , за которое
амплитуда
колебаний
уменьшится в
e раз время релаксации.
Общая физика. «Физика колебаний и волн»
x A0 e t cos t
A A0 e t
t
A A0 e t

18.

Кафедра физики
Свободные затухающие колебания.
x, A
x A0 e t cos t
A A0 e t
A0
t
T
A A0 e t
Колебание x A0 e t cos t не
периодическое и не гармоническое.
Периодичность
колебания
нарушается затуханием.
Следовательно, к затухающим колебаниям неприменимо понятие
периода или частоты.
Но: при малом затухании можно пользоваться понятием периода как
промежутка времени между двумя последующими максимумами или
минимумами колеблющейся физической величины.
Выражение для периода:
Общая физика. «Физика колебаний и волн»
T 2 2
02 2

19.

Кафедра физики
Свободные затухающие колебания.
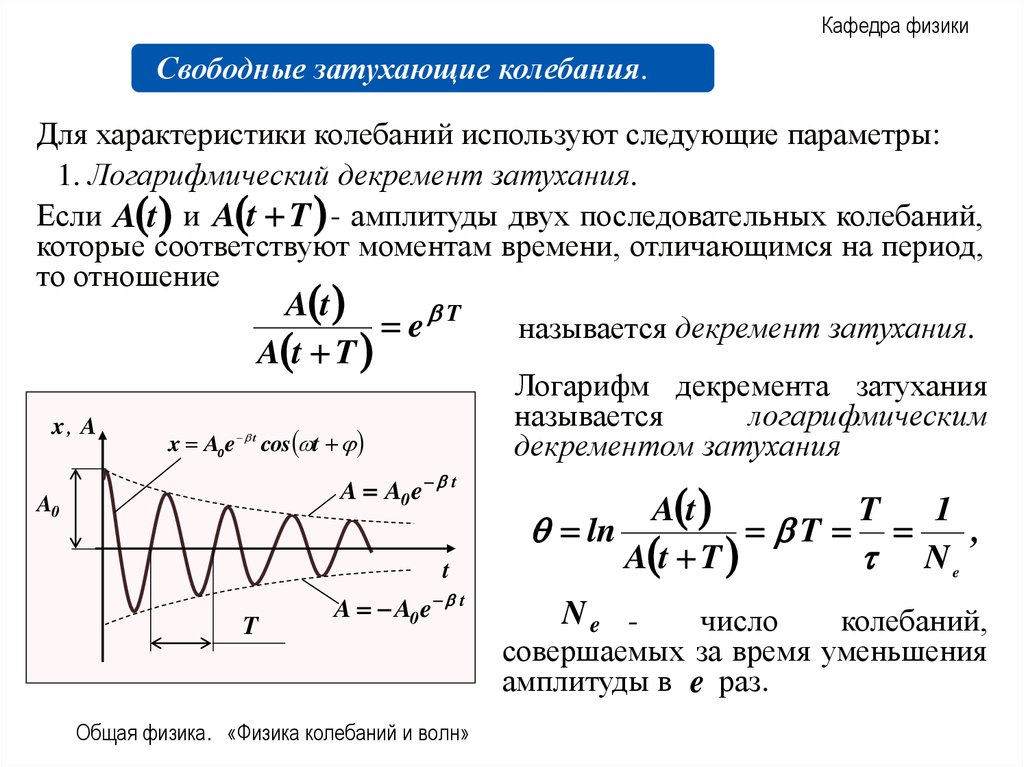
Для характеристики колебаний используют следующие параметры:
1. Логарифмический декремент затухания.
Если A t и A t T - амплитуды двух последовательных колебаний,
которые соответствуют моментам времени, отличающимся на период,
то отношение
A t
e T
A t T
x, A
x A0 e t cos t
A A0 e t
A0
t
T
A A0 e t
Общая физика. «Физика колебаний и волн»
называется декремент затухания.
Логарифм декремента затухания
называется
логарифмическим
декрементом затухания
A t
T
1
ln
T
,
A t T
Ne
Ne -
число
колебаний,
совершаемых за время уменьшения
амплитуды в e раз.

20.

Кафедра физики
Свободные затухающие колебания.
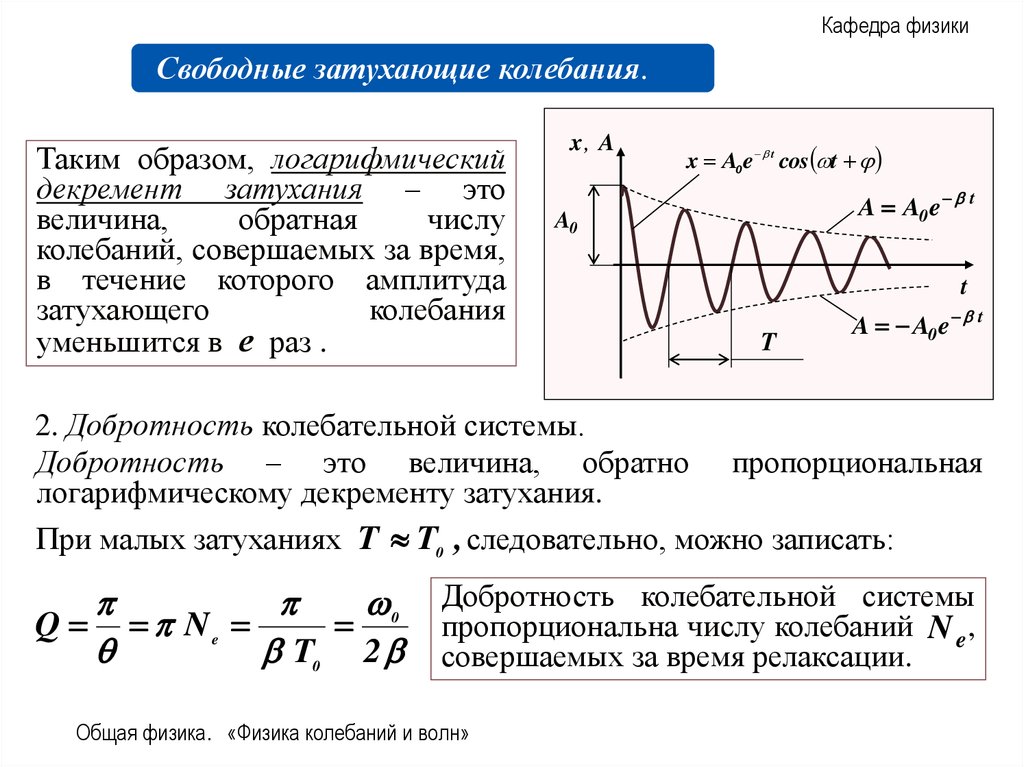
Таким образом, логарифмический
декремент затухания – это
величина,
обратная
числу
колебаний, совершаемых за время,
в течение которого амплитуда
затухающего
колебания
уменьшится в е раз .
x, A
x A0 e t cos t
A A0 e t
A0
t
T
A A0 e t
2. Добротность колебательной системы.
Добротность – это величина, обратно пропорциональная
логарифмическому декременту затухания.
При малых затуханиях T T0 , следовательно, можно записать:
0
Q Ne
T0 2
Добротность колебательной системы
пропорциональна числу колебаний N e ,
совершаемых за время релаксации.
Общая физика. «Физика колебаний и волн»