Колебания. Кинематика гармонических колебаний

1.

Колебания
Кинематика гармонических колебаний
Колебания – повторяющийся во времени процесс
x(t ) A1 cos t A2 sin t
x (t ) A cos( t 0 )
A
A12 A22 , tg 0 A2 A1
A – амплитуда колебаний
– угловая частота
( t + 0) – фаза колебаний
0 – начальная фаза
T
2
– гармонические колебания
– период колебаний

2.

Колебания
Комплексная форма гармонических колебаний
z x iy
– алгебраическая форма
z (cos i sin )
z e i
i 1
– тригонометрическая форма
– показательная форма
– мнимая единица
e i cos i sin
x2 y 2
– формула Эйлера
– модуль комплексного числа
tg y x , – фаза комплексного числа

3.

Колебания
Комплексная форма гармонических колебаний
Сложение комплексных чисел
z z1 z2 ( x1 x2 ) i ( y1 y2 )
Геометрически сложение производится по правилу параллелограмма
iy
z z1 z2
z2
z1
x
Умножение комплексных чисел
z z1 z 2 1 2 e i ( 1 2 )

4.

Колебания
Комплексная форма гармонических колебаний
Комплексная форма гармонической функции
x A cos( t 0 )
z Aei ( t 0 )
График гармонических колебаний
iy
x Re( z ) A cos( t 0 )
y Im( z ) A sin( t 0 )
z
t
0
x
– гармонические
колебания

5.

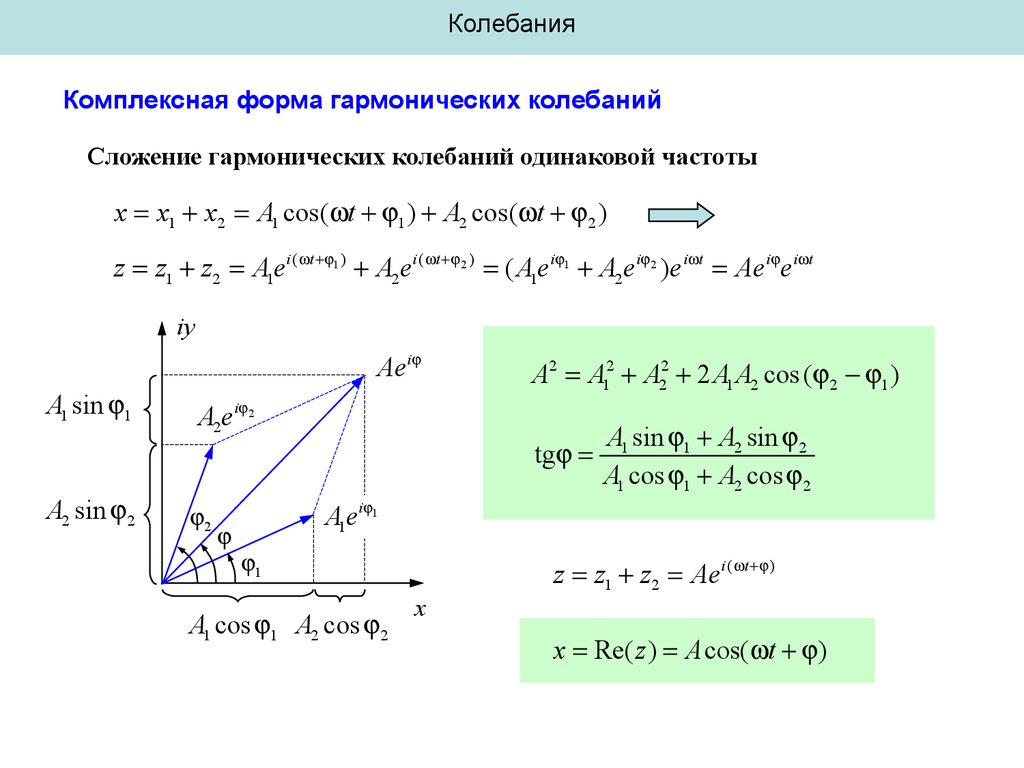
Колебания
Комплексная форма гармонических колебаний
Сложение гармонических колебаний одинаковой частоты
x x1 x2 A1 cos( t 1 ) A2 cos( t 2 )
z z1 z2 A1ei ( t 1 ) A2 ei ( t 2 ) ( A1ei 1 A2ei 2 )e i t Aei ei t
iy
Aei
A1 sin 1
A2 sin 2
A2ei 2
2
A2 A12 A22 2 A1 A2 cos ( 2 1 )
tg
A1 sin 1 A2 sin 2
A1 cos 1 A2 cos 2
A1ei 1
1
A1 cos 1 A2 cos 2
x
z z1 z2 Aei ( t )
x Re( z ) A cos( t )

6.

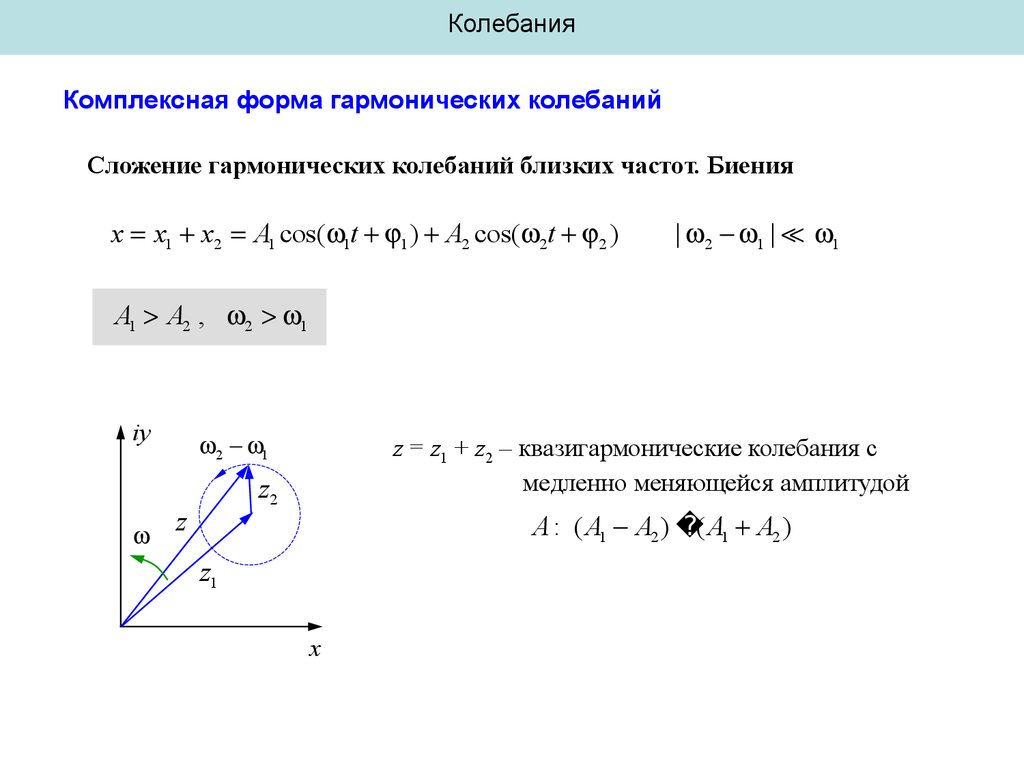
Колебания
Комплексная форма гармонических колебаний
Сложение гармонических колебаний близких частот. Биения
x x1 x2 A1 cos( 1t 1 ) A2 cos( 2t 2 )
| 2 1 | 1
A1 A2 , 2 1
iy
2 1
z = z1 + z2 – квазигармонические колебания с
медленно меняющейся амплитудой
z2
z
A : ( A1 A2 ) ( A1 A2 )
z1
x

7.

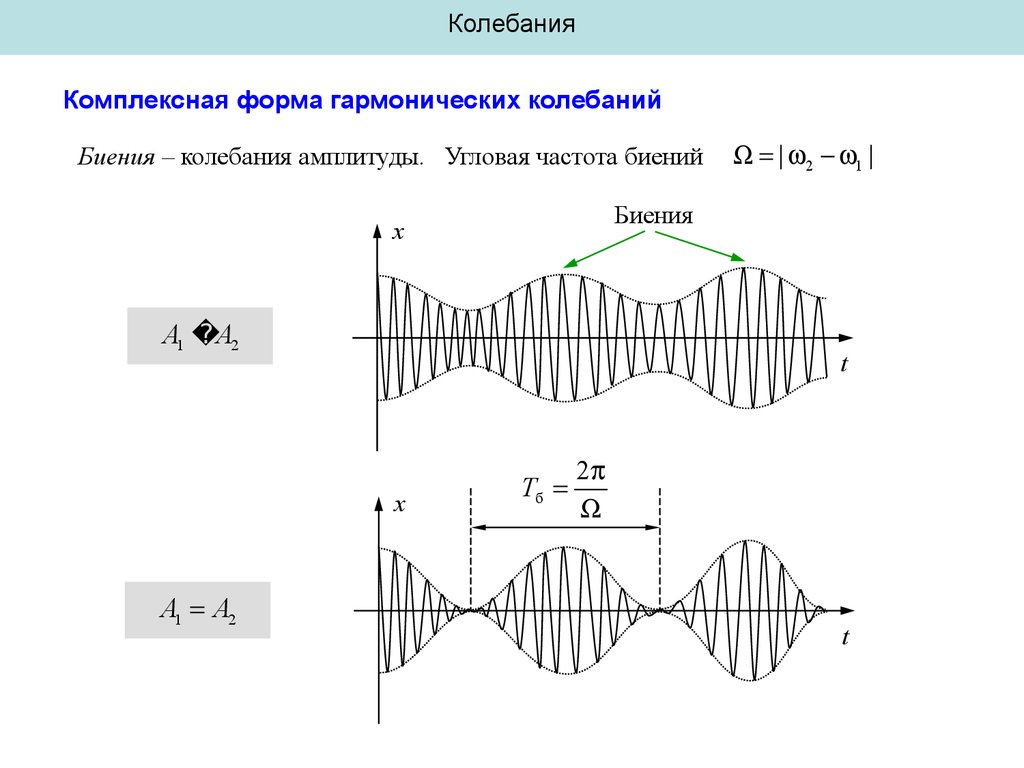
Колебания
Комплексная форма гармонических колебаний
Биения – колебания амплитуды. Угловая частота биений
Биения
x
A1 A2
t
x
A1 A2
| 2 1 |
Tб
2
t

8.

Колебания
Гармонический осциллятор
Уравнение движения системы, совершающей движение около положения
равновесия при малых отклонениях
& f ( x )
mx&
При малых отклонениях
& kx
mx&
x 2 x 0
f ( x ) kx
:m
– уравнение динамики гармонических колебаний
Система, совершающая малые колебания, называется
линейным, или гармоническим осциллятором.
Общее решение
2 k m
x A cos( t 0 )

9.

Колебания
Гармонический осциллятор
Пружинный маятник
& f ( x )
mx&
k
m
0
f ( x ) kx
x
x 2 x 0
и
x A cos( t 0 )
T
k
m
2
m
2
k

10.

Колебания
Гармонический осциллятор
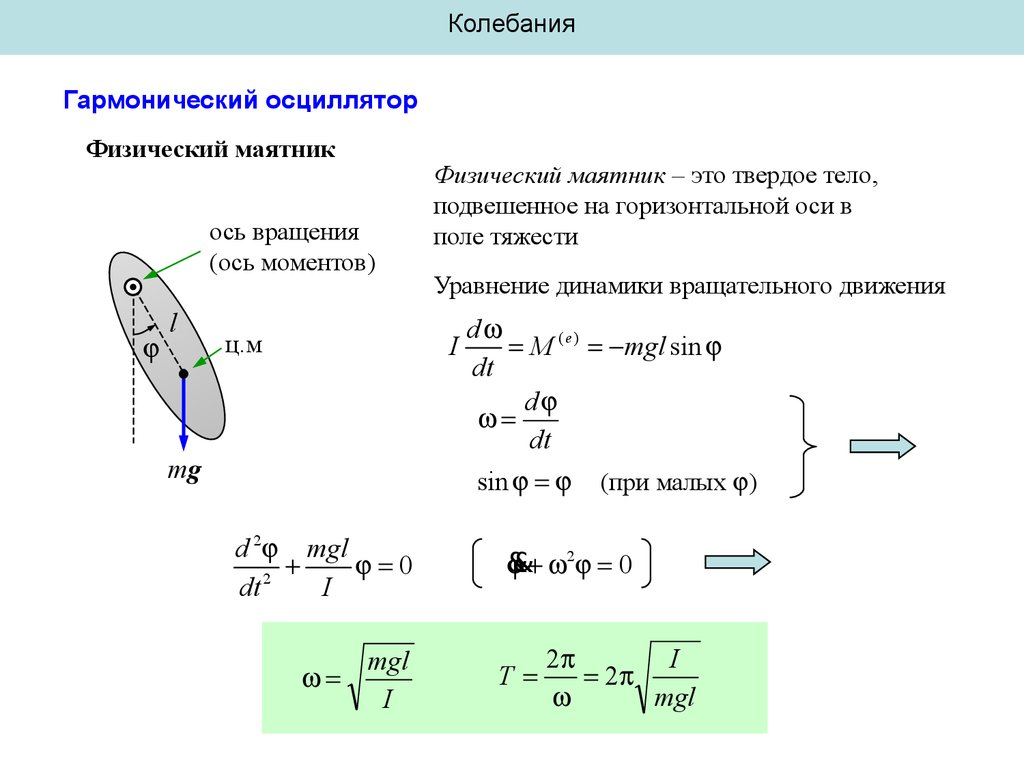
Физический маятник
ось вращения
(ось моментов)
l
ц.м
Физический маятник – это твердое тело,
подвешенное на горизонтальной оси в
поле тяжести
Уравнение динамики вращательного движения
I
mg
d
M ( e ) mgl sin
dt
d
dt
sin
d 2 mgl
0
2
dt
I
mgl
I
(при малых )
&
& 2 0
T
2
I
2
mgl

11.

Колебания
Гармонический осциллятор
Математический маятник
l
m
Математический маятник – это физический маятник,
состоящий из материальной точки, подвешенной на
твердом невесомом стержне
I ml 2
(из формул для физического маятника)
mg
g
l
T 2
l
g

12.

Колебания
Затухающие колебания
Линейный осциллятор при наличии трения
v
Fтр bx& – жидкое трение
Fтр
Уравнение движения
x 2 x 02 x 0
Решение ищем в виде
& kx bx& : m
mx&
b
k
, 02
2m
m
– уравнение динамики затухающих колебаний
x A0 e i t
A0 e i t ( 2 2i 02 ) 0
2 2i 02 0

13.

Колебания
Затухающие колебания
Решение квадратного уравнения
i 02 2 i
x A1e ( i ) t A2 e ( i ) t e t ( A1e i t A2 e i t )
Общее решение
При малом затухании
x Ae t cos( t )
b 2m
1
02 2
0
– уравнение затухающих колебаний
– коэффициент затухания
– время затухания
(время, за которое амплитуда уменьшается в e раз)

14.

Колебания
Затухающие колебания
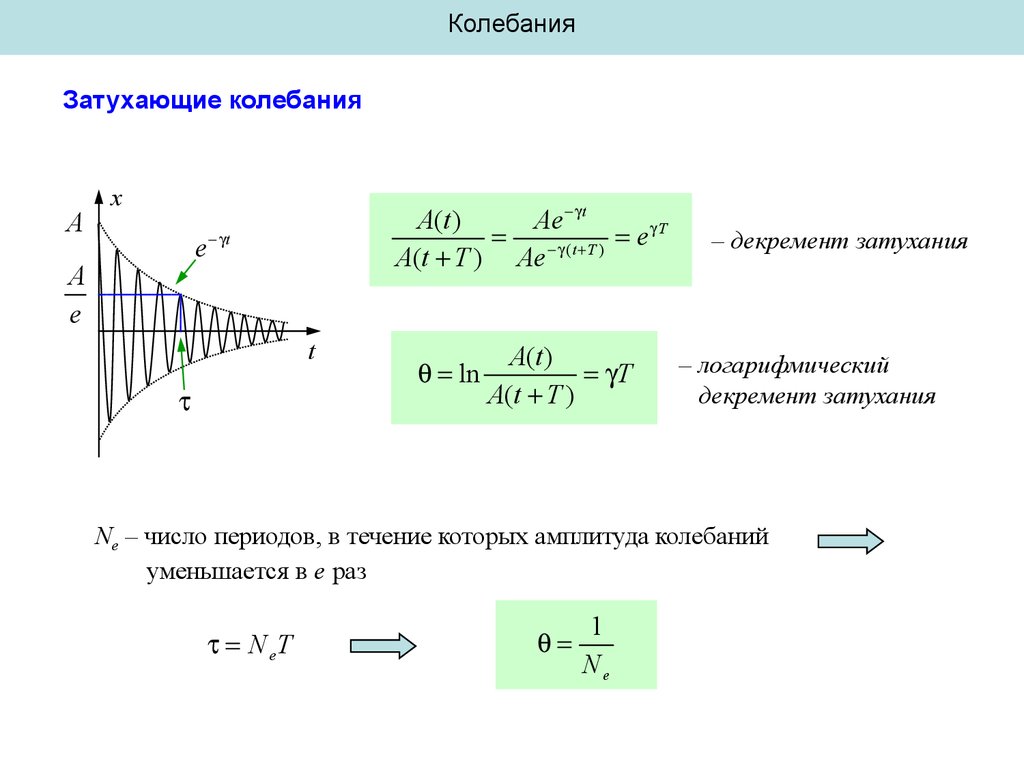
A
x
A(t )
Ae t
( t T ) e T
A(t T ) Ae
e t
A
e
t
ln
A(t )
T
A(t T )
– декремент затухания
– логарифмический
декремент затухания
Ne – число периодов, в течение которых амплитуда колебаний
уменьшается в e раз
N eT
1
Ne