Колебания. Основные понятия и классификация колебаний

1.

Тема 5
Часть1
Основные понятия и классификация колебаний
Колебаниями называются движения или процессы, которые
характеризуются определенной повторяемостью во времени.
Физическая природа колебаний может быть разной, поэтому различают
колебания механические, электромагнитные и электромеханические.
Пример колебательного процесса: движение м.т. по окружности с
постоянной скоростью.
x(0) R cos 0
Такое движение – суперпозиция колебательных движений
во взаимно перпендикулярных направлениях.
Любой повторяющийся процесс, исключая случайный, можно представить в
виде конечной суммы колебаний.

2.

Колебания называются свободными (или собственными),
если они совершаются за счет первоначально сообщенной
энергии при последующем отсутствии внешних воздействий
на колебательную систему (систему, совершающую колебания).
Вынужденными называют такие колебания, которые
происходят в системе под периодическим внешним воздейст–
вием

3.

5.1 Гармонические колебания
Гармонические колебания описываются уравнением
x A cos( 0t )
Или, т.к. cos sin(
2
),
x A sin( 0t )
2
, где
x
- смещение колеблющейся величины из положения равновесия
A – амплитуда колебаний
0 – круговая (циклическая) частота
– начальная фаза колебаний
( 0t )
– фаза колебаний

4.

Минимальный промежуток времени, по истечении которого
колебательный процесс повторяется, называется периодом
колебаний T
0 (t T ) 0t 2
Откуда
T
2
0
Величина, обратная периоду,, называется частотой колебаний
Циклическая частота
1
T
0 2
Гармонические колебания – колебания, при которых колеблю–
щаяся величина изменяется со временем по закону синуса
(косинуса); при этом параметры
.
Колебательная система, в которой могут происходить гармони–
ческие колебания, называется гармоническим осциллятором

5.

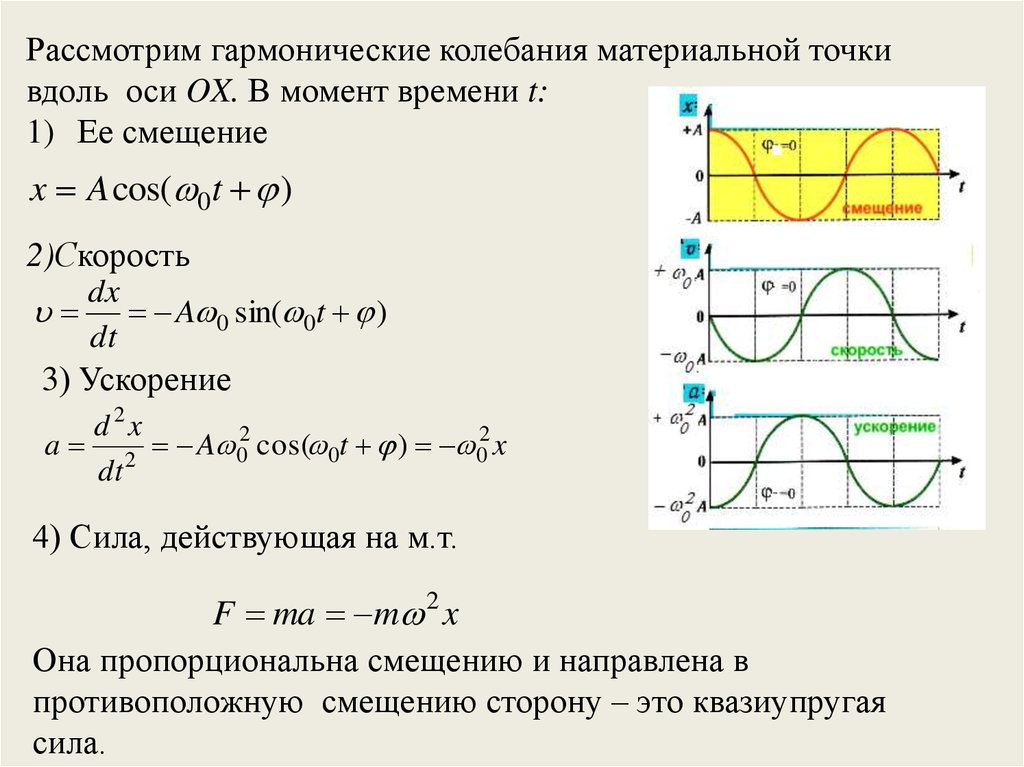
Рассмотрим гармонические колебания материальной точки
вдоль оси OX. В момент времени t:
1) Ее смещение
x A cos( 0t )
2)Скорость
dx
A 0 sin( 0t )
dt
3) Ускорение
d 2x
a 2 A 02 cos( 0t ) 02 x
dt
4) Сила, действующая на м.т.
F ma m 2 x
Она пропорциональна смещению и направлена в
противоположную смещению сторону – это квазиупругая
сила.

6.

5) Кинетическая энергия м.т.
m 2 mA2 02
T
sin 2 0t
2
2
6) Потенциальная энергия материальной точки, совершающей
гармонические колебания под действием квазиупругой силы
F:
x
x
2 2
2 2
m
x
mA
0
2
0
Fdx m 0 xdx
cos2 ( 0t )
2
2
0
0
7) Полная энергия
1
E T mA 2 02
2

7.

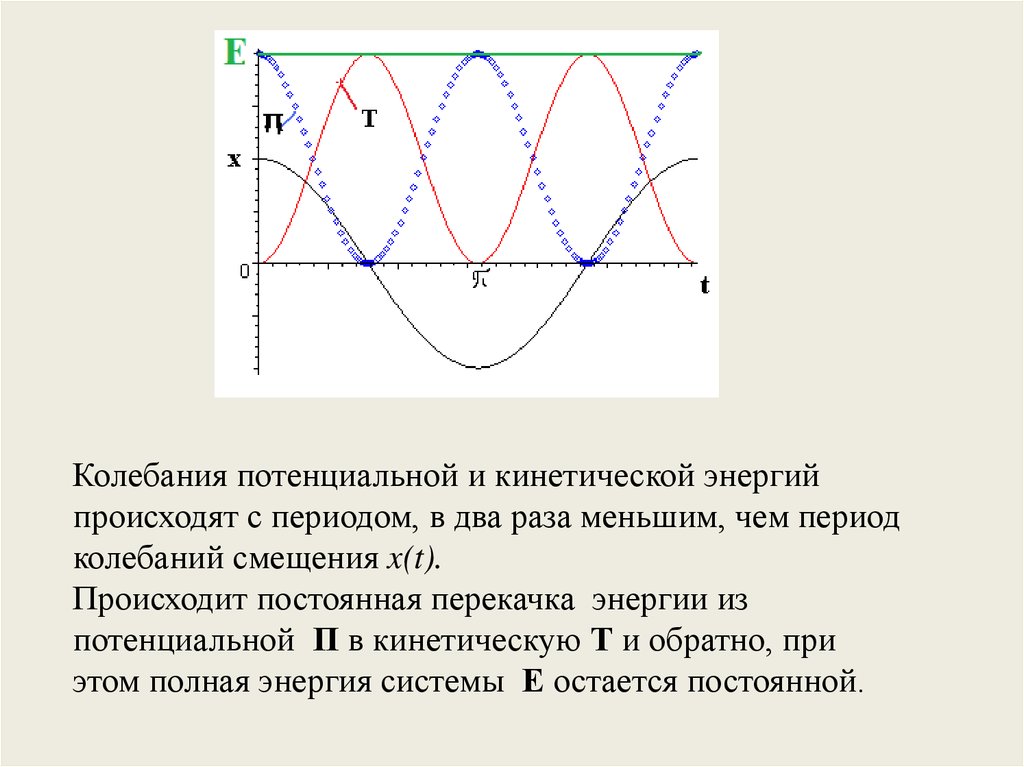
Колебания потенциальной и кинетической энергий
происходят с периодом, в два раза меньшим, чем период
колебаний смещения x(t).
Происходит постоянная перекачка энергии из
потенциальной П в кинетическую Т и обратно, при
этом полная энергия системы Е остается постоянной.

8.

8) Дифференциальное уравнение гармонических колебаний
м.т.:
mx kx
k
0
m
Его решение:
k
x x 0
m
2
x 0 x
m
T 2
k
x A cos( 0t )
Или с учетом того, что cos sin( )
2
x(t ) A sin( 0t )
2
0

9.

Гармонические колебания изображаются графически
методом векторных диаграмм.

10.

Колеблющуюся величину представляют и комплексным числом
i
e cos i sin
i ( 0t )
~
x Ae
~
Re( x ) A cos( 0t ) x
Обозначение
Re вещественной части обычно опускается
i ( 0t )
x Ae
В теории колебаний принимается, что колеблющаяся величина x
равна вещественной части комплексного выражения,
стоящего в этом равенстве справа.

11.

Гармонический осциллятор. Пружинный, физический
и математический маятники
Гармоническим осциллятором называется система,
совершающая колебания, описываемые уравнением вида:
2
x 0 x
0
Пружинный маятник.
mx kx
k
x x 0
m
k
0
m
m
T 2
k

12.

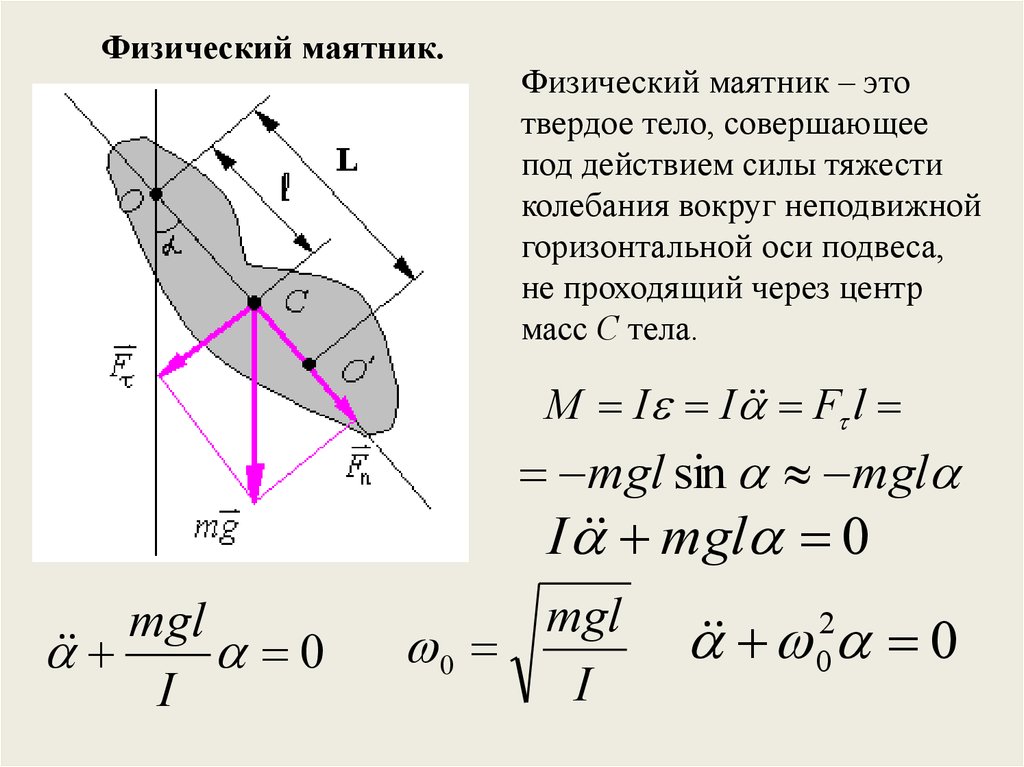
Физический маятник.
Физический маятник – это
твердое тело, совершающее
под действием силы тяжести
колебания вокруг неподвижной
горизонтальной оси подвеса,
не проходящий через центр
масс С тела.
M I I F l
mgl sin mgl
I mgl 0
mgl
0
I
mgl
0
I
0
2
0

13.

0
2
0
0 cos( 0t )
;
2
I
L
T
2
2
0
mgl
g
I
L
ml
– приведенная длина физического маятника

14.

Математический маятник.
Математический маятник – это идеализированная система,
состоящая из материальной точки массой m, подвешенной на
нерастяжимой невесомой нити, и колеблющаяся под действием
силы тяжести.
I ml 2
I
ml 2
l
T 2
2
2
mgl
mgl
g
l
T 2
g
Приведенная длина физического маятника – это длина
такого математического маятника, период колебаний
которого совпадает с периодом колебаний данного
физического маятника.

15.

Свободные гармонические колебания
в колебательном контуре.
IR UC s
dI
Q
L
IR 0
dt
C
R
1
Q Q
Q 0
L
LC
R 0:
1
Q
Q 0
LC
(*)
1
Q
Q 0
LC
Q Q0 cos( 0t )

16.

1
0
LC
T 2 LC
Формула Томсона
I Q 0Q0 sin( 0t ) I 0 cos( 0t )
2
Q Q0
UC
cos( 0t ) U 0 cos( 0t )
C C
Отсюда видно, что колебания тока опережают по фазе колебания
заряда на .
2

17.

Колебания электрической энергии , запасенной в конденсаторе
CU 2 CU 20
WE
cos2 ( 0t )
2
2
Колебания энергии магнитного поля в катушке
LI 2 LI 20 2
WH
sin ( 0t )
2
2
Полная энергия, запасенная в контуре
CU 2 LI 2 C Q02
L Q02
Q02
2
2
W
cos ( 0t )
sin ( 0t )
const
2
2
2
2C
2 LC
2C
Связь амплитудных значений тока и напряжения
LI02 CU 20
W
2
2
L
U0
I0
C

18.

Превращения энергии в колебательном контуре
q q0 cos( 0t )
I I 0 sin( 0t )
В последующие полпериода
процесс повторяется в обратном
направлении.
t 0 : qmax
q02 -мгновенной разрядке С препятствует s ,
q0 , E
2C сдерживающая процесс нарастания I в
катушке.
1
LI02
t T , q 0, I max I 0 , E
4
2
- С разряжен, ток и энергия магнитного
поля максимальны. Мгновенному
убыванию тока I препятствует
появление s .
2
q2
t T , I 0, q q0 , E 0
4
2C
- С зарядился индукционным током
катушки.