Электромагнитные колебания. Уравнение гармонических колебаний

1.

Электромагнитные колебания
Колебания
называются
свободными,
если
они
совершаются за счет первоначально сообщенной энергии,
без дальнейшего внешнего воздействия на колебательную
систему.
Колебания в
электрической цепи
называются
затухающими, если они
происходят в контуре с
омическим
сопротивлением
Колебания в
электрической цепи
называются
вынужденными, если
они происходят под
действием
периодически
изменяющегося
внешнего
воздействия,
например
переменного
напряжения
Колебания в
электрической цепи
называются
свободными, если они
происходят в контуре
вблизи состояния
системы с максимумом
потенциальной энергии
(заряженного
конденсатора). В
отсутствии омического
сопротивления –
колебания
характеризуют частотой
собственных колебаний.

2.

Уравнение гармонических колебаний
Свободный колебательный контур –
электрическая цепь, состоящая из
0
конденсатора с емкостью С и катушки с
индуктивностью L.
IR 1 2 si
R 0
q
1 2
C
dq
I
dt
1
LC
T 2 LC
dI
si L
dt
d 2q 1
q 0
q
(
t
)
q
cos(
t
)
2
0
0
0
dt
LC
q( t ) q0
UС
cos( 0t 0 ) U 0 cos( 0t 0 )
C
C
dI
U L U С L U 0 cos( 0t 0 )
dt
dq
I
q0 0 sin( 0t 0 ) I 0 cos 0t 0
dt
2

3.

Энергия гармонических колебаний
0
q 2 LI 2 q02 cos 2 ( 0t 0 ) Lq02 02 sin 2 ( 0t 0 )
W
2C
2
2C
2
q02 LI 02
W
2C
2
1
LC

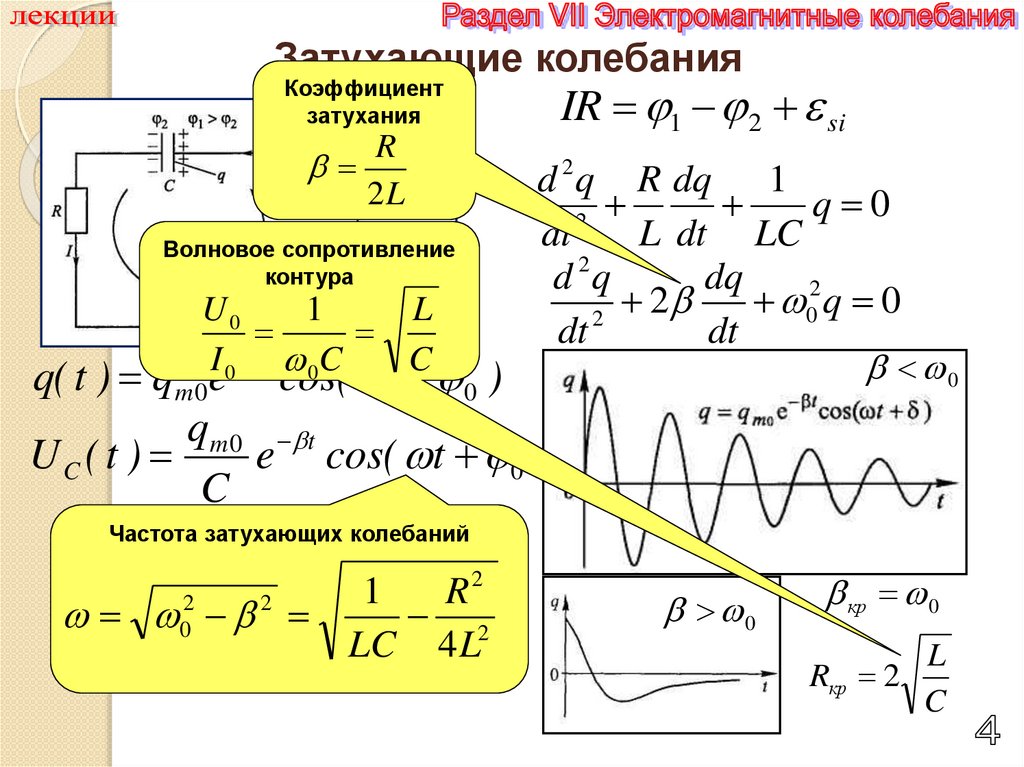
4.

Затухающие колебания
Коэффициент
затухания
R
2L
IR 1 2 si
d 2 q R dq 1
q 0
2
dt
L dt LC
Волновое сопротивление
контура
d 2q
dq
2
2
U0
1
L
0q 0
2
dt
dt
0C
C
0
q( t ) qm 0 eI 0 t cos(
t
0 )
qm 0 t
UC ( t )
e cos( t 0 )
C
Частота затухающих колебаний
2
0
2
1
R2
2
LC 4 L
0
кр 0
L
Rкр 2
C

5.

Затухающие колебания
dq
qm 0 e t cos( t 0 ) sin( t 0 )
dt
2
2
cos( t 0 )
sin( t 0 )
2
2
2
2
I( t )
qm 0 e t
qm 0e t 0 cos cos( t 0 ) sin sin( t 0 )
I ( t ) qm 0 e t 0 cos( t 0 )
tg
cos 0
sin 0
В случае
гармонических
колебаний на
/2
2
Ток опережает по фазе
напряжение на конденсаторе
более чем на /2

6.

Затухающие колебания
Добротность
Коэффициент
затухания
R
2L
Время жизни
Логарифмический
декремент затухания
a( t )
ln
a( t T )
a( t )
e
T
ln
e
T
a( t )
qm 0 e t
Число колебаний за
t
e
e
время, когда
( t )
амплитуда
qm 0 e
1
1
уменьшается в e раз
Ne
T
1
T
Q N e
T
W W0 e 2 t
dW
2 t
W
WT
2 T
W
W
Q
WT 2

7.

Затухающие колебания

8.

Вынужденные колебания
IR 1 2 si
m
d 2 q R dq 1
q
cos t
2
dt
L dt LC
L
m
d 2q
dq
2
2
0 q
cos t
2
dt
dt
L
m cos t
q( t ) qm 0 e t cos( затt 0 ) qm cos( t )
q( t ) qm cos( t )
m
qm
L
4
2
0
2 2
2
2
2
tg 2
0 2

9.

Вынужденные колебания
1. Сила тока
dq
I( t )
qm sin( t ) qm cos t
dt
2
Im
m
L
I ( t ) I m cos t
4
2
0
2 2
2
Im
m
C
2
R 2 L 1
2
tg tg ctg
2
2
2
0
2
L 1 C
R
2. Напряжение на сопротивлении R
U R I m R cos t U Rm cos t
U Rm I m R
m
Z

10.

Вынужденные колебания
q
UC
C
qm
Im
U Cm
C C
qm
UC
cos( t ) U Cm cos( t ) U Cm cos t
C
2
3. Напряжение на конденсаторе
U Cm
m 2
4
2 2
2
0
2
U Cm
2
m
2
C R L 1
2
C
4. Напряжение на катушке индуктивности
U Lm I m L
dI
U L si L
dt
U L I m L sin( t ) U Lm cos t
2
m L
m 2
U
U Lm
4
2
0
2 2
2
Lm
2
R L 1
2
C
2

11.

Вынужденные колебанияУровень половины
Резонанс
Амплитудные резонансные кривые
R
C 1
LC R
рез L
L Q
рез max 02 2 2 0
энергии колебаний с
резонансной частотой
полуширина
R
L
Фазовые резонансные кривые

12.

Вынужденные колебания
Векторная диаграмма напряжений
q
dI
IR L m cos t
C
dt
tg
L 1 C
R
U R U C U L m cos t
U R I m R cos t
Im
UC
cos t
С
2
U L I m L cos t
2
0
В условиях резонанса
U Cm
В условиях
резонанса контур
обладает только
активным
сопротивлением
Im
L
L
Im
U Lm I m 0 L I m
0С
C
C
Резонанс
напряжений

13.

Вынужденные колебания
Переменный ток
1. Переменный ток в цепи,
обладающей только
активным сопротивлением
2. Переменный ток в цепи,
обладающей только
индуктивностью
Im
m
Im
L
m
R
3. Переменный ток в цепи,
обладающей только емкостью
I m m С
Im
Емкостное
сопротивление
XC 1
C
4. Переменный ток в цепи,
обладающей емкостью и
индуктивностью
m
индуктивное
сопротивление
Переменный ток представляет собойреактивное
X L в L
вынужденные электрические колебания
сопротивление
цепи, обладающей индуктивностью, емкостью
и активным сопротивлением.
L 1 С
X L 1
С

14.

Вынужденные колебания
Переменный ток
5. Полное сопротивление цепи - импеданс
Im
m
R 2 L 1
C
2
m
Z
Z R L 1
2
C
2
Мощность переменного тока
Pt IU
1. Мгновенное значение мощности переменного тока
I mU m
cos( 2 t ) cos
Pt I m cos( t )U m cos t
2
2. Среднее значение мощности переменного тока
I mU m
I mU m
cos( 2 t ) cos
P
cos
2
2
1
R
R
cos
2
2
2
2
2
1 tg
R
X
1
R L
C

15.

Вынужденные колебания Действующее
(эффективное) значение
силы тока
Действующие значения
1
P I mU m cos
2
U Rm U m cos I m R
1 2
P ImR
2
P I R
2
эф
Im
I эф
2
T
T
1 2
2
I эф R I ( t )Rdt
T0
I
2
эф
1 2
I ( t )dt
T0
T
Um
U эф
2
2
U эф
T
2
1 U (t )
dt
R
T0 R
Действующее
(эффективное) значение
напряжения
U
2
эф
1
U 2 ( t )dt
T0
Коэффициент мощности
P I эфU эф cos

16.

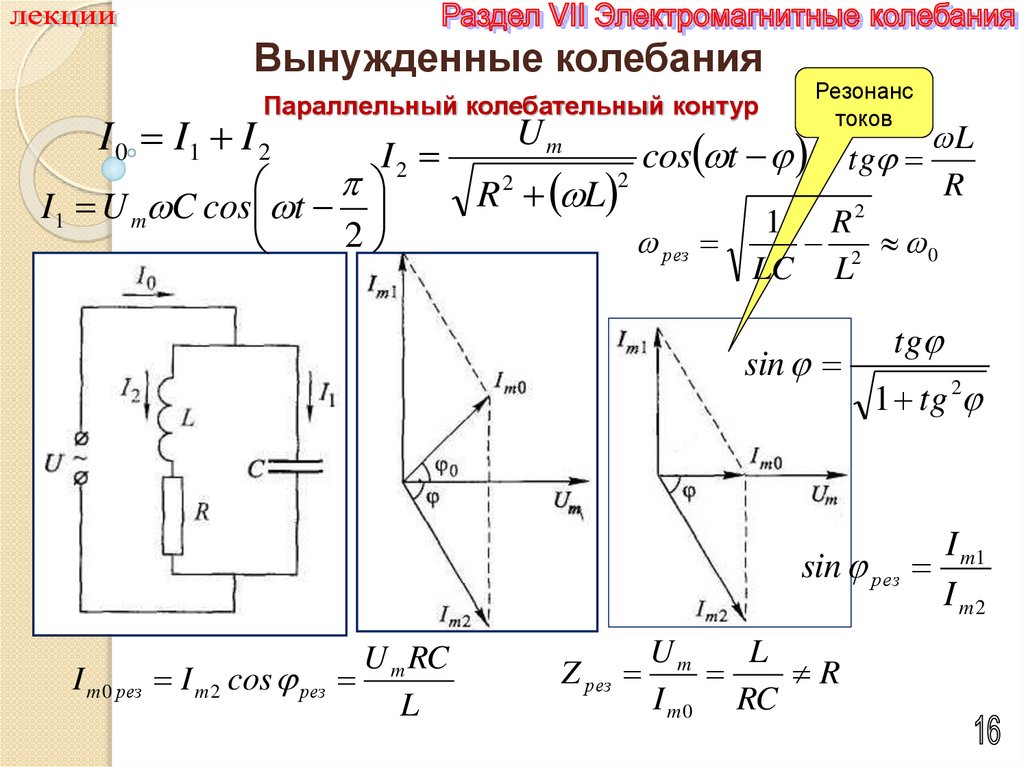
Вынужденные колебания
Параллельный колебательный контур
I 0 I1 I 2
Резонанс
токов
L
I2
cos t tg
2
2
R
R
L
2
I1 U m C cos t
1
R
2
рез
2 0
Um
LC
L
sin
tg
1 tg 2
I m1
sin рез
I m2
U m RC
I m 0 рез I m 2 cos рез
L
Z рез
Um
L
R
I m 0 RC

17.

ВОПРОСЫ ВЫНОСИМЫЕ НА 2 КОЛЛОКВИУМ
1.
2.
3.
4.
5.
6.
Гармонические электромагнитные колебания
Затухающие электромагнитные колебания
Вынужденные электромагнитные колебания
Резонанс в различных контурах. Метод диаграмм.
Переменный ток. Закон Ома. Импеданс.
Переменный ток . Мощность.