Similar presentations:
Электромагнитные колебания
1.
Электромагнитные колебания1. Свободные колебания в электрическом
контуре без активного сопротивления
2. Свободные затухающие электрические
колебания
3. Вынужденные электрические колебания
4. Переменный ток
5. Работа и мощность переменного тока
2.
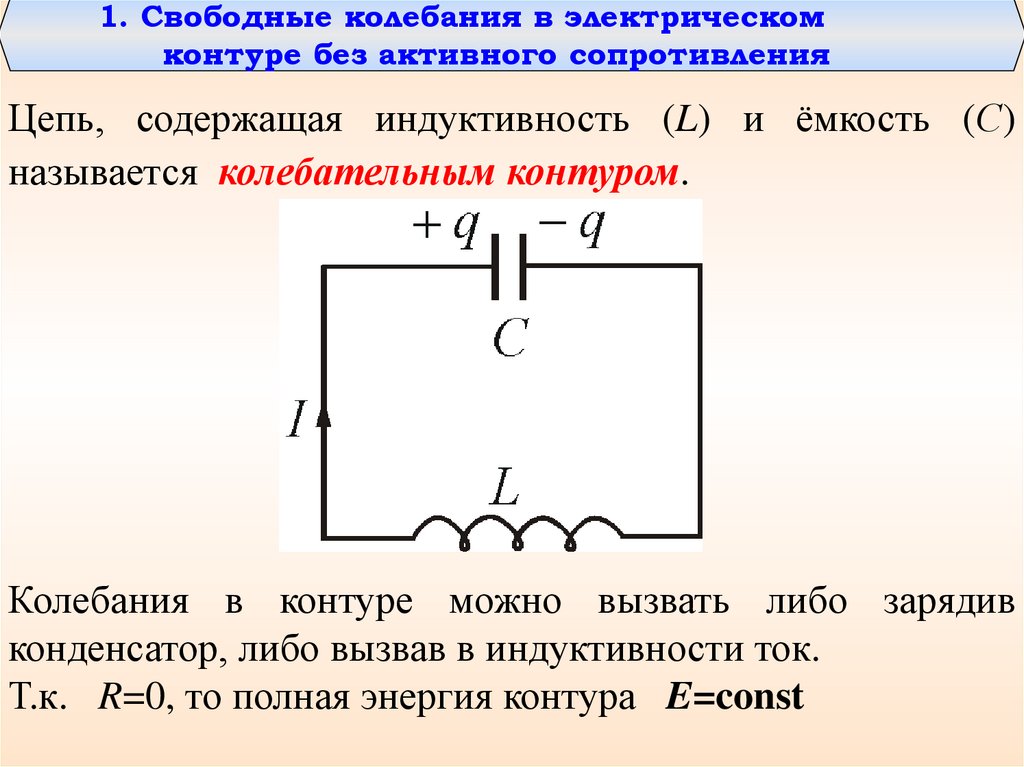
1. Свободные колебания в электрическомконтуре без активного сопротивления
Цепь, содержащая индуктивность (L) и ёмкость (С)
называется колебательным контуром.
Колебания в контуре можно вызвать либо зарядив
конденсатор, либо вызвав в индуктивности ток.
Т.к. R=0, то полная энергия контура E=const
3.
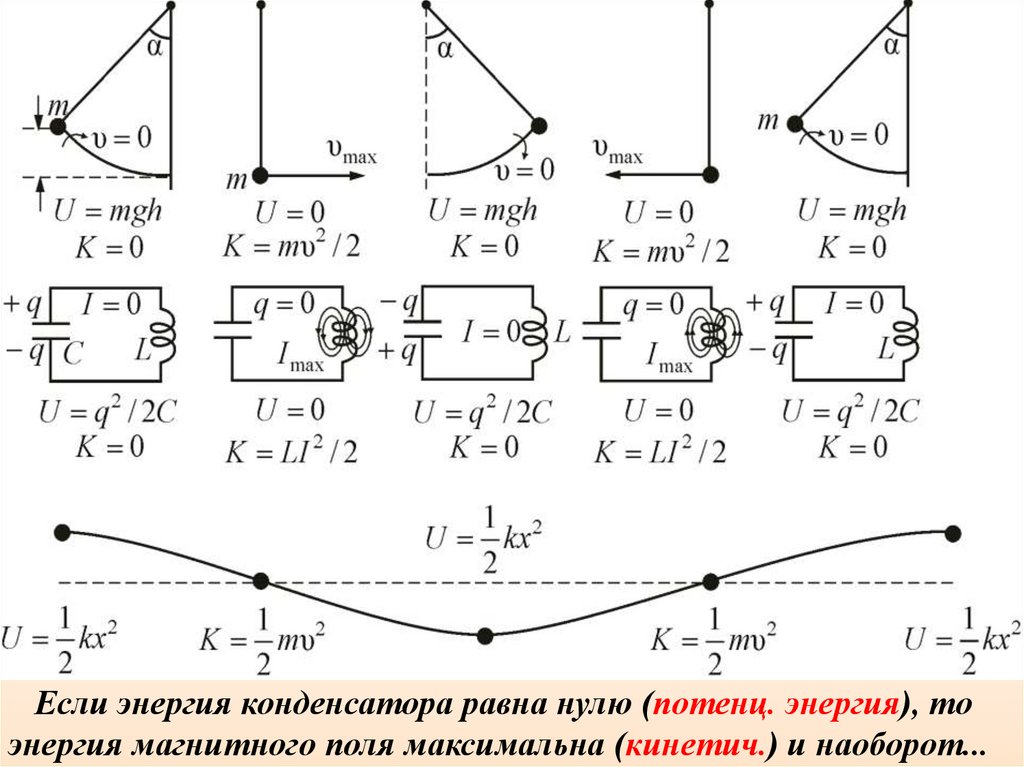
Если энергия конденсатора равна нулю (потенц. энергия), тоэнергия магнитного поля максимальна (кинетич.) и наоборот...
4.
5.
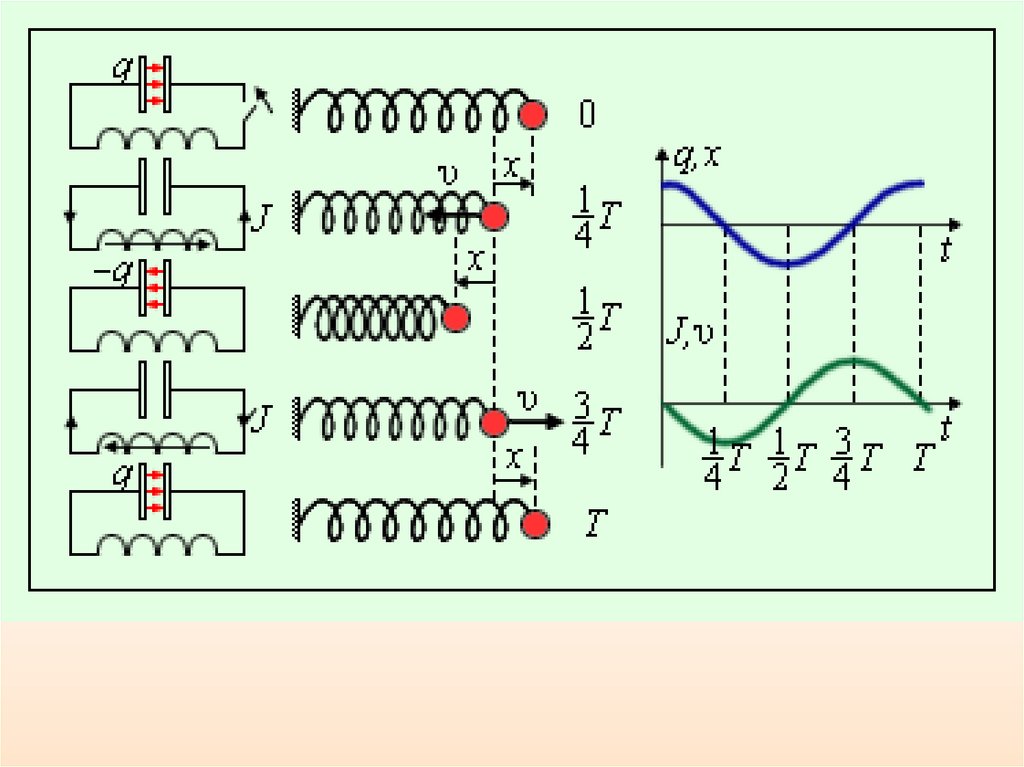
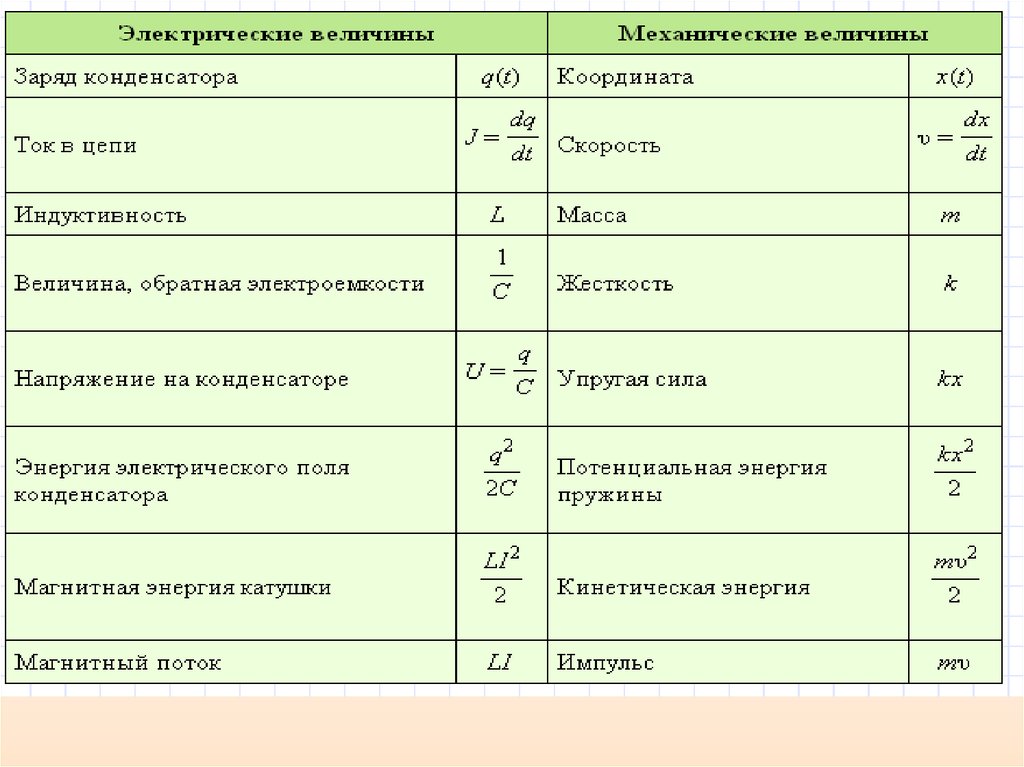
Из сопоставления электрических и механическихколебаний следует, что:
энергия
электрического
поля
аналогична
потенциальной энергии упругой деформации
•энергия магнитного поля аналогична кинетической
энергии;
• Индуктивность L играет роль массы m
• 1/С – роль коэффициента жесткости k
• Заряду q соответствует смещение маятника х
• Силе тока I ~ скорость υ
• Напряжению U ~ ускорение а
6.
7.
В соответствии ссохранения энергии)
законом
Кирхгофа
(и
законом
dq L dI ,
I
, i
dt
dt
q
dI
R=0
L
C
dt
2
d q 1
q 0
2
dt
LC
Дифференциальное
колебаний:
2
dq
2
ω0 q 0,
2
dt
уравнение
ω0
электромагнитных
1
LC
Собственная
частота
контура
Решение уравнения - гармоническая функция:
q qm cos( ω0t φ)
8.
q qm cos( ω0t φ)Таким образом, заряд на обкладке конденсатора
изменяется по гармоническому закону с частотой
ω0 – собственная частота контура.
Период колебаний определяется по формуле Томсона:
1 2π
T
2π LC
ν ω0
T 2π LC
9.
Напряжениеqm
U
cos ω 0t φ U m cos ω0t φ на
конденсаторе
C
L Закон Ома
L – волновое
Um Im
сопротивл.
для контура
C
C
[Ом].
Ток в цепи:
dq
π
I
ω0 qm sin ω0t φ I m cos ω0t φ
dt
2
I m ω 0 qm
Амплитуда тока
На емкости ток опережает напряжение на π/2.
На индуктивности наоборот напряжение опережает ток на
π/2.
10.
2. Свободные затухающие электрические колебанияВсякий
реальный
контур
обладает
активным
сопротивлением R. Энергия, запасенная в контуре,
постепенно расходуется в этом сопротивлении на
нагревание, вследствие чего колебания затухают.
11.
По второму закону Кирхгофаq
dI
IR L
c
dt
Уравнение свободных
затухающих колебаний в
контуре R,L и C
2
dq
dq
2
2
β
ω
0q 0
2
dt
dt
решение этого уравнения имеет вид:
q q0 e
βt
cos( ωt φ),
β R / 2 L, - коэффициент затухания
1
ω0
- собственная частота контура
LC
2
Частота
1
R
2
2
ω ω 0 β или ω
затухающих
2
LC 4 L
колебаний
12.
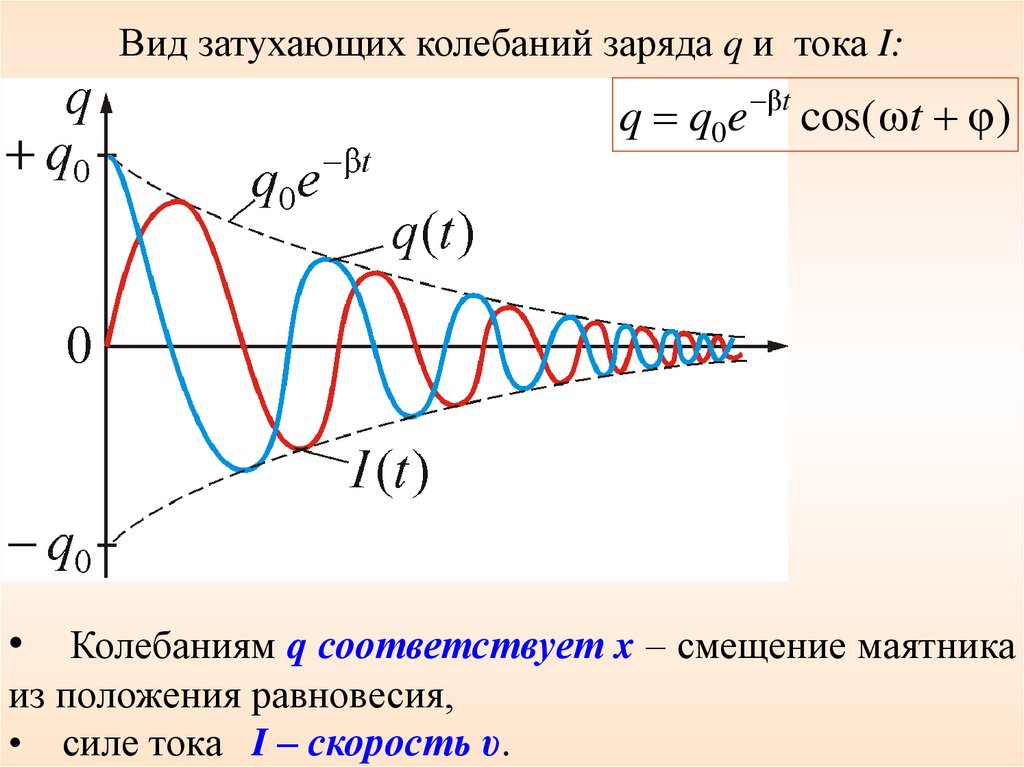
Вид затухающих колебаний заряда q и тока I:q q0e
βt
cos( ωt φ)
Колебаниям q соответствует x – смещение маятника
из положения равновесия,
• силе тока I – скорость υ.
13.
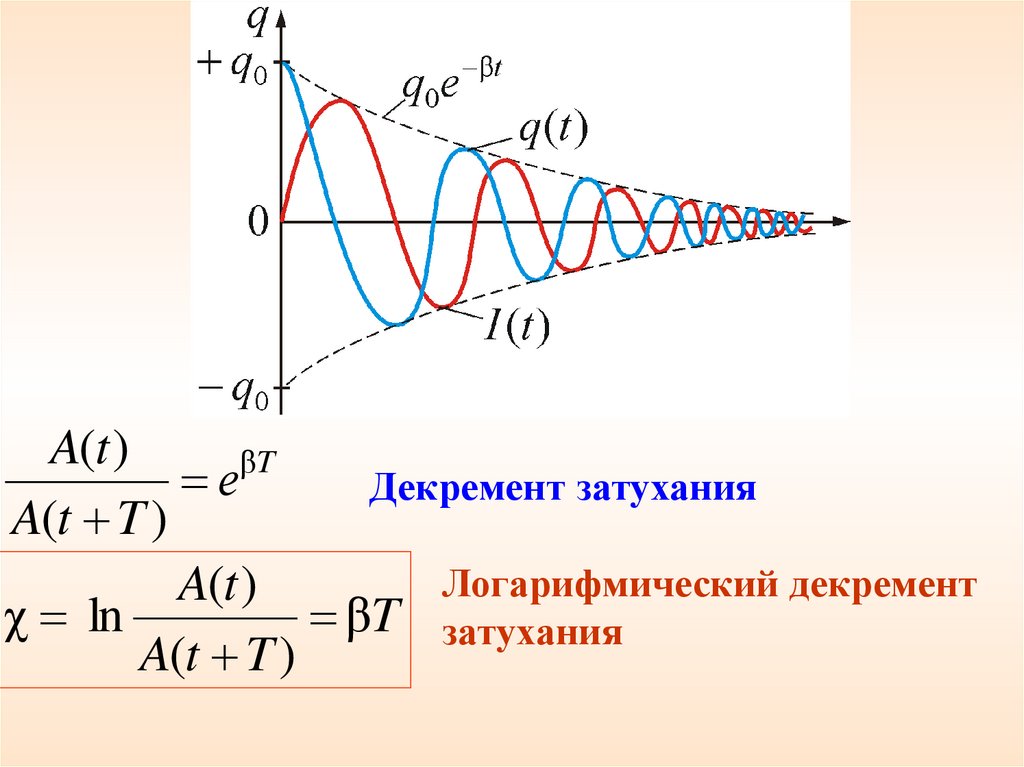
A(t )еβT
Декремент затухания
A(t T )
Логарифмический декремент
A(t )
χ ln
βT затухания
A(t T )
14.
Т.к. коэффициент затуханияПериод затухающих колебаний
Тогда
πR
χ βT
Lω
R
β
2L
2π
T
;
ω
R, L, ω – определяются параметрами контура,
следовательно, и χ является характеристикой контура.
Если затухание невелико β 2 ω 02
ω ω0
1
,
LC
C
χ πR
L
14
15.
Добротность колебательного контура Qопределяется как величина обратно
пропорциональная χ (Чем меньше
затухание, тем выше добротность)
1
π
Q
χ
Время затухания – время за которое
амплитуда колебаний уменьшается в е раз
1
Ne
T T
Число колебаний совершаемых
за время затухания
1
χ
Nе
W
Q 2π
ΔW
то
Q πN е
W – энергия контура в данный момент,
ΔW – убыль энергии за один период, следующий
за этим моментом
16.
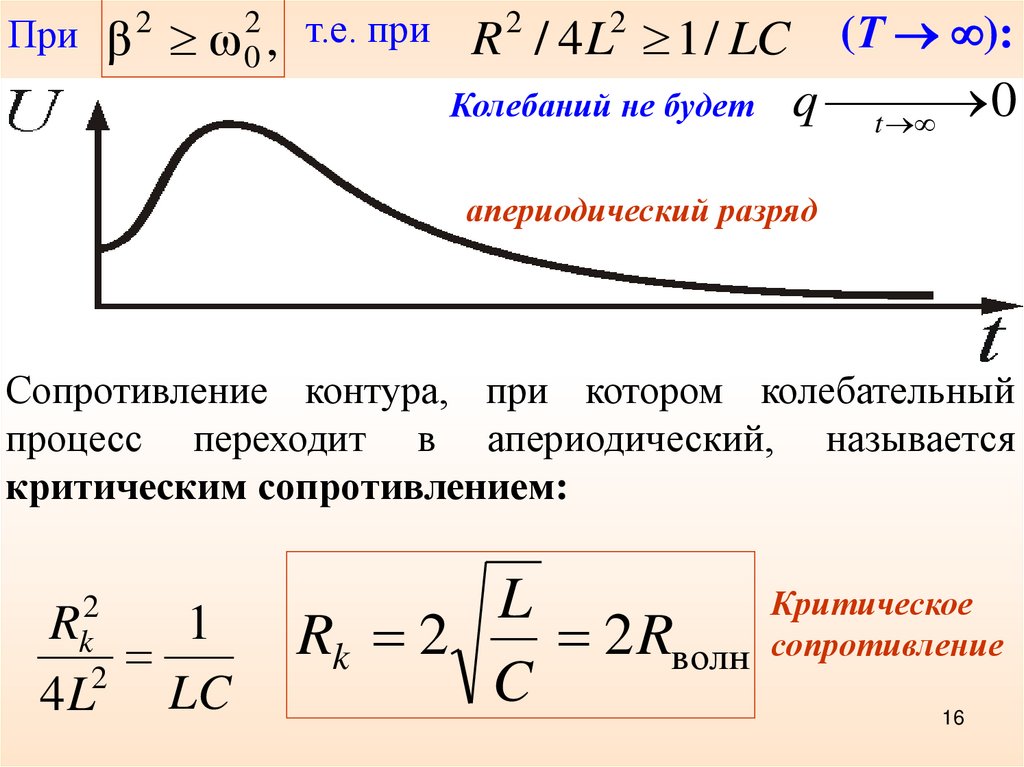
Приβ
2
ω 02 ,
т.е. при
(Т ):
R / 4 L 1 / LC
2
2
Колебаний не будет
q
0
t
апериодический разряд
Сопротивление контура, при котором колебательный
процесс переходит в апериодический, называется
критическим сопротивлением:
2
Rk
2
1
4 L LC
L
Rk 2
2 Rволн
C
Критическое
сопротивление
16
17.
3. Вынужденные электрические колебанияК контуру, изображенному на рис. подадим переменное
напряжение U : U U m cos ωt
2
dq
dq
Um
2
2
β
ω
q
cos
ω
t
0
2
dt
L
dt
уравнение вынужденных электрических колебаний
совпадает с вынужденными механическими колебаниями.
18.
Это уравнение совпадает с дифференциальнымуравнением механических колебаний.
Решение уравнения при больших t:
q qm cos( ωt φ)
Здесь амплитуда колебаний заряда:
2
1
2
2
qm U m / ω R ωL
U
/
ω
R
(
R
R
)
m
L
C
ωC
2
19.
1Z R ωL
ωC
2
2
1
X RL RC ωL
ωC
полное
сопротивление цепи
(импеданс)
– реактивное
сопротивление
R – активное сопротивление отвечает за потерю
мощности в цепи.
X – реактивное сопротивление, определяет величину
энергии пульсирующей в цепи с частотой 2ω.
20.
Резонанс напряжений (последовательный резонанс)При последовательном
соединении R, L, С, при
1
ωL
ωC
наблюдается резонанс.
ωрез
Тогда
2
ω0
2β
2
Угол сдвига фаз между током и
напряжением обращается в нуль
(φ = 0)
Z R
U U R , а UC и UL одинаковы по амплитуде
и противоположны по фазе. Такой вид резонанса называется
резонансом напряжения или последовательным резонансом.
21.
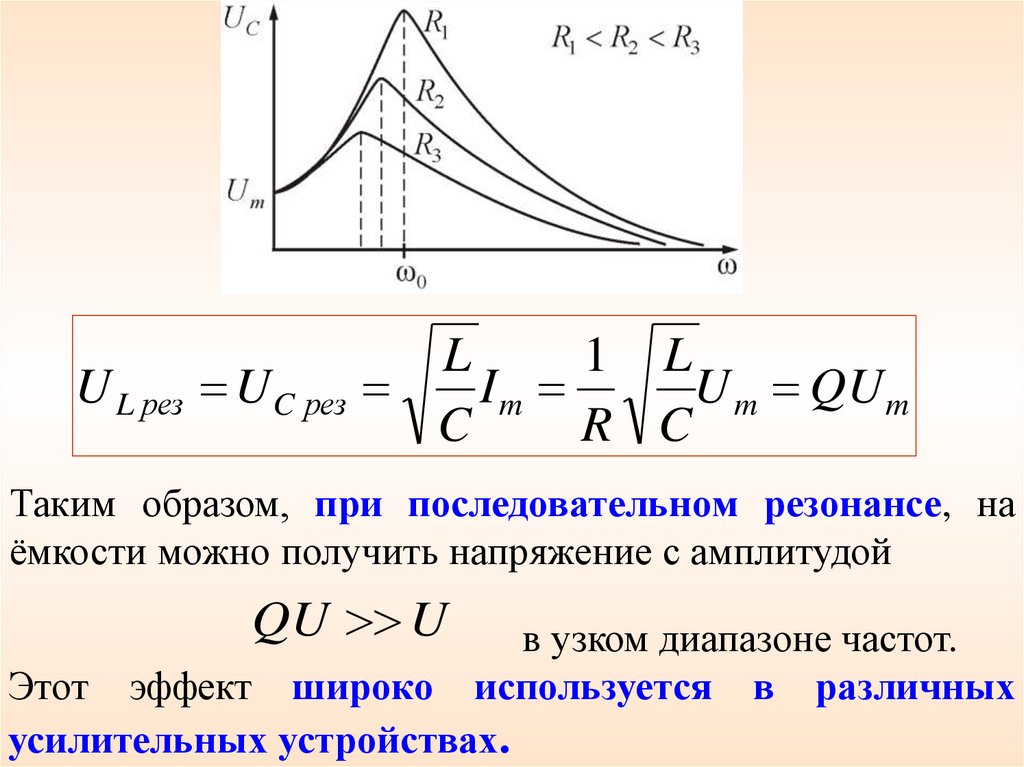
U L рез U C резL
1 L
Im
U m QU m
C
R C
Таким образом, при последовательном резонансе, на
ёмкости можно получить напряжение с амплитудой
QU U
в узком диапазоне частот.
Этот эффект широко используется в различных
усилительных устройствах.
22.
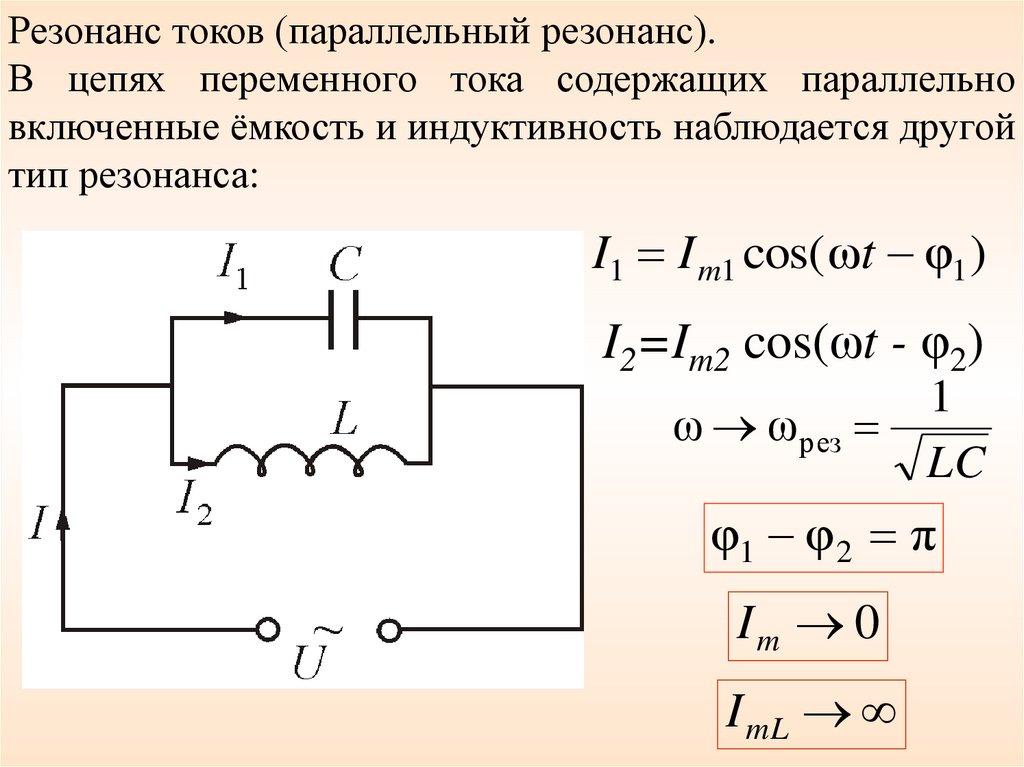
Резонанс токов (параллельный резонанс).В цепях переменного тока содержащих параллельно
включенные ёмкость и индуктивность наблюдается другой
тип резонанса:
I1 I m1 cos( ωt φ1 )
I2=Im2 cos(ωt - φ2)
ω ωрез
1
LC
φ1 φ 2 π
Im 0
I mL
23.
При R = 0, L = 0:Um
I m1
1 / ωC
I1 I m1 cos( ωt φ1 )
tg φ1 = - ∞ т.к. φ1 = (2n +3/2 )π,
где n = 1,2,3….
При R =0, C =∞: I2=Im2 cos(ωt - φ2)
Im2 = U /ωL
tg φ2 = +∞ , т.е.
φ1 φ 2 π
φ2= (2n + 1/2 ) π
где n = 1,2,3…..
24.
Таким образом разность фаз в ветвях цепиφ1 φ 2 π
т.е. токи противоположны по фазе
1
I m I m1 I m 2 U m ωC
ωL
1
Если ω ω рез
то
LC
Im 0
I m1 I m 2
Ёмкость конденсатора можно подобрать так, что в
результате резонанса ток в подводящих цепях резко
уменьшается, зато ток через индуктивность возрастёт
25.
ω ω рез1
LC
Явление уменьшения амплитуды тока во внешней цепи
и резкого увеличения тока в катушке индуктивности, при
приближении частоты приложенного напряжения ω к ωрез
называется резонансом токов, или параллельным
резонансом
(Используется в резонансных усилителях, приемниках,
а также в индукционных печах для разогрева металла).
26.
4. Переменный токПри
рассмотрении
электрических
колебаний
приходится иметь дело с токами, изменяющимися во
времени – переменными токами:
I = I0 sin( t + )
Закон Ома и вытекающие из него правила Кирхгофа
были установлены для постоянного тока. Однако они
остаются справедливыми и для мгновенных значений
изменяющегося тока.
27.
Электромагнитные сигналы распространяются по цепи соскоростью света с.
• Пусть l – длина электрической цепи.
• Время распространения сигнала в данной цепи
t l / c.
• Если t T то такие токи называются
квазистационарными (Т – период колебаний тока).
• При этом условии мгновенное значение силы тока во
всех участках цепи будет постоянным.
• Для частоты 50Гц условие квазистационарности будет
выполняться при длине цепи ~ 100 км
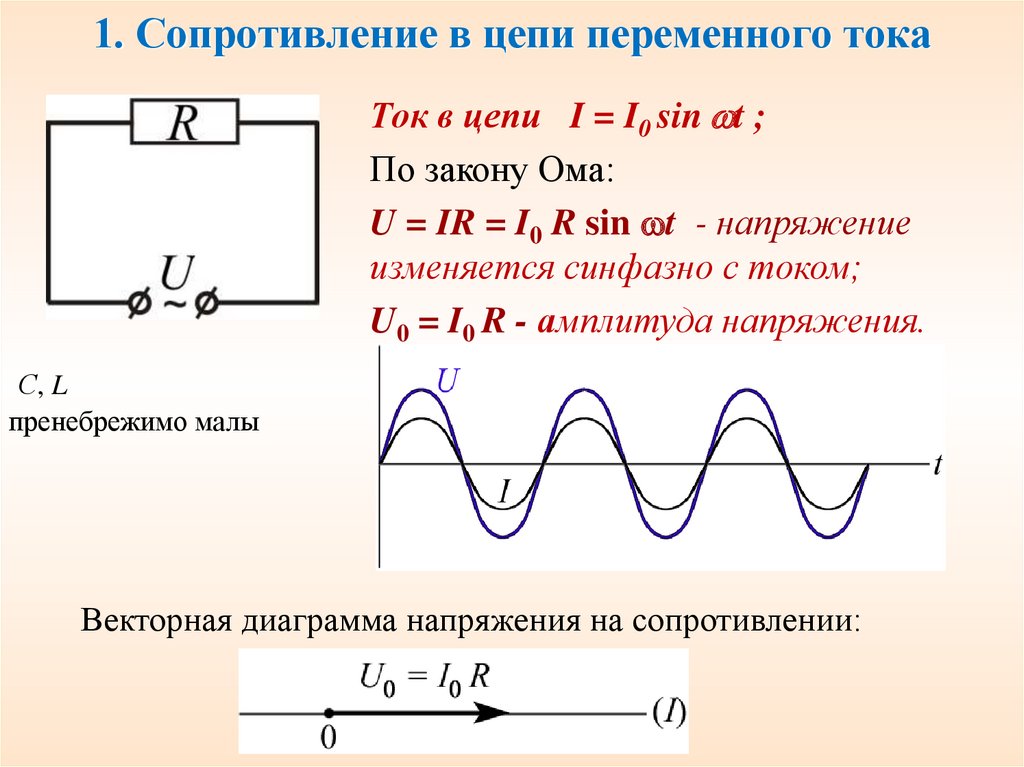
28. 1. Сопротивление в цепи переменного тока
Ток в цепи I = I0 sin t ;По закону Ома:
U = IR = I0 R sin t - напряжение
изменяется синфазно с током;
U0 = I0 R - амплитуда напряжения.
С, L
пренебрежимо малы
Векторная диаграмма напряжения на сопротивлении:
29.
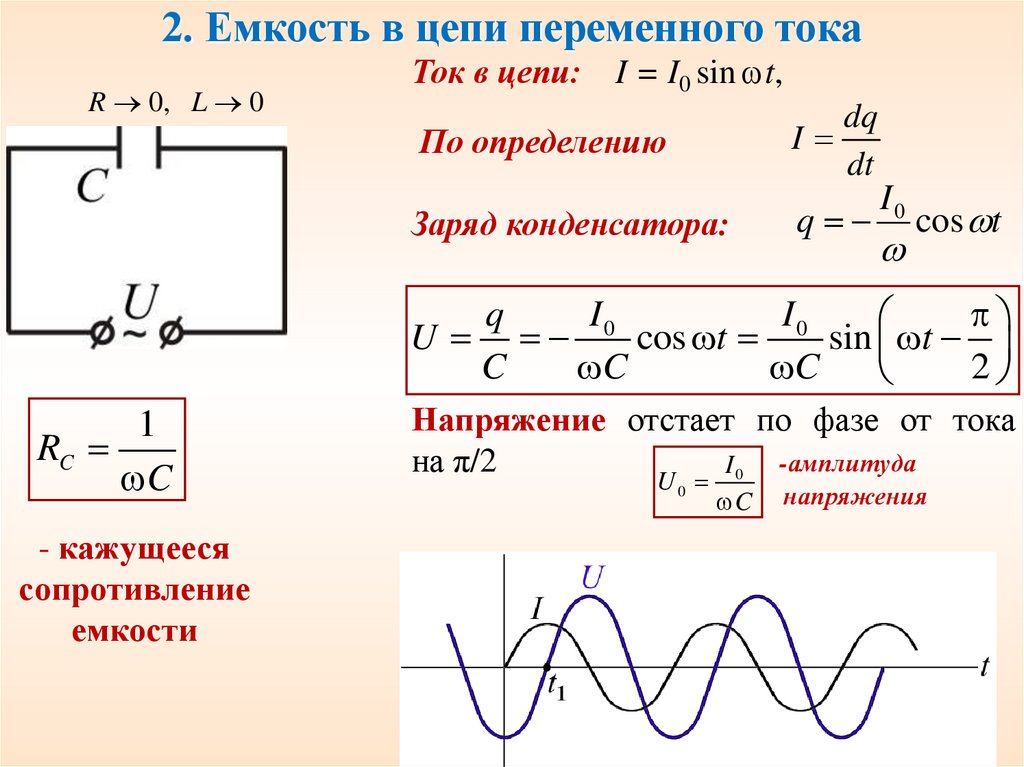
2. Емкость в цепи переменного токаR 0, L 0
Ток в цепи:
I = I0 sin t,
dq
I
dt
По определению
Заряд конденсатора:
q
I0
cos t
I0
I0
q
U
cos t
sin t
C
C
C
2
1
RC
C
- кажущееся
сопротивление
емкости
Напряжение отстает по фазе от тока
на π/2
I 0 -амплитуда
U0
C
напряжения
30.
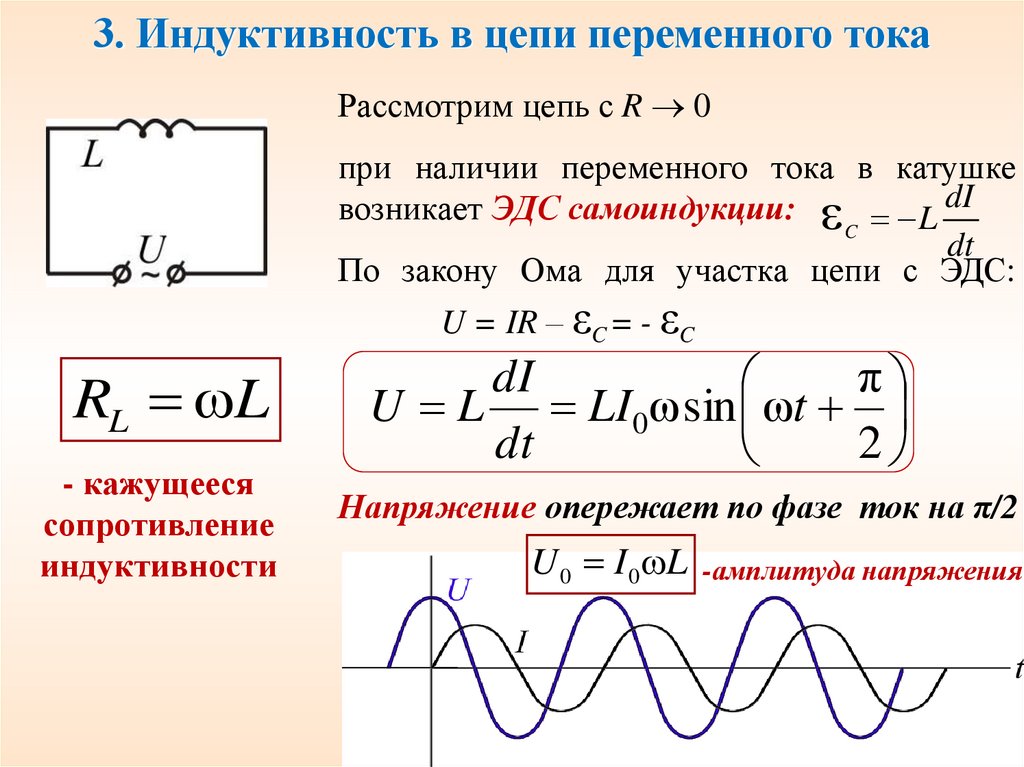
3. Индуктивность в цепи переменного токаРассмотрим цепь с R 0
при наличии переменного тока в катушке
возникает ЭДС самоиндукции: L dI
C
dt
По закону Ома для участка цепи с ЭДС:
U = IR – εC = - εC
RL L
- кажущееся
сопротивление
индуктивности
dI
π
U L LI0ω sin ωt
dt
2
Напряжение опережает по фазе ток на π/2
U 0 I 0 L
-амплитуда напряжения
31.
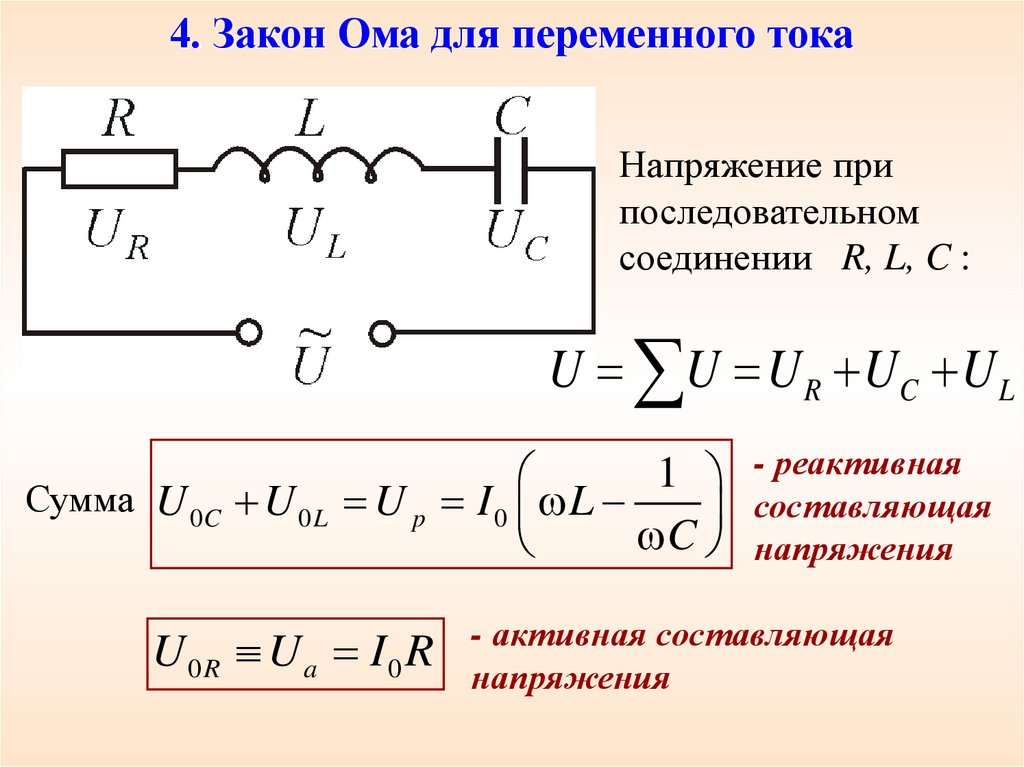
4. Закон Ома для переменного токаНапряжение при
последовательном
соединении R, L, C :
U U U R UC U L
Сумма U 0C U 0 L
1 - реактивная
U p I 0 L
составляющая
C напряжения
U0R U a I0 R
- активная составляющая
напряжения
32.
Результирующееколебание:
l
L
U = U0 sin ( t + )
Фаза:
1
U p L C
tg
Ua
R
Амплитуда напряжения:
U0 I0
1
R L
C
2
2
- закон Ома для переменного тока
33.
Полное сопротивление цепи:Rполн
U0
1
2
R L
I0
C
2
R – активное (омическое) сопротивление
1
Х = L
C
- реактивное сопротивление
R – активное сопротивление отвечает за потерю
мощности в цепи.
X – реактивное сопротивление, определяет величину
энергии пульсирующей в цепи с частотой 2ω.
34.
Элементы цепи и соответствующие им импедансы:Импеданс соединений:
Z Z k - последовательного
k
1
1
- параллельного
Z
k Zk
Закон Ома в
комплексной форме
I
Z
1
R i L
C
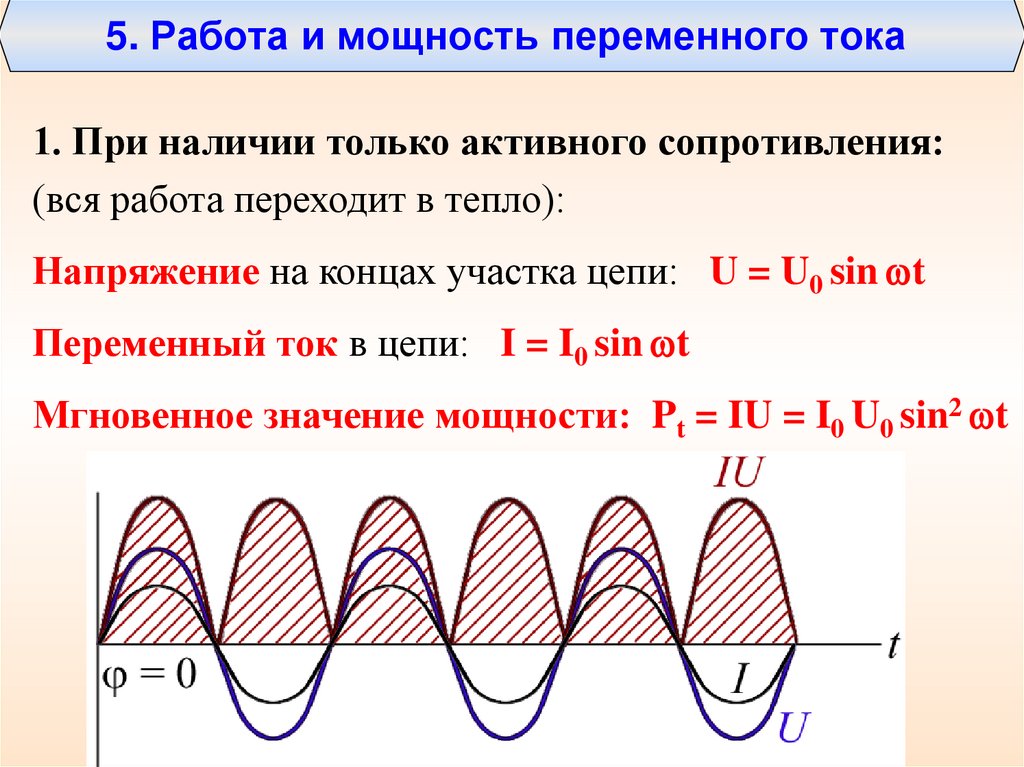
35. 5. Работа и мощность переменного тока
1. При наличии только активного сопротивления:(вся работа переходит в тепло):
Напряжение на концах участка цепи: U = U0 sin t
Переменный ток в цепи: I = I0 sin t
Мгновенное значение мощности: Pt = IU = I0 U0 sin2 t
36.
Работа переменного тока за dt:A = Pt dt = Im Um sin2 t dt
Работа переменного тока за период Т:
1
А I mU mT
2
1
Cредняя мощность P I mU m или
2
1 2
P RIm
2
Действующие (или эффективные) значения тока и
напряжения:
Im
I
2
Um
U
2
37.
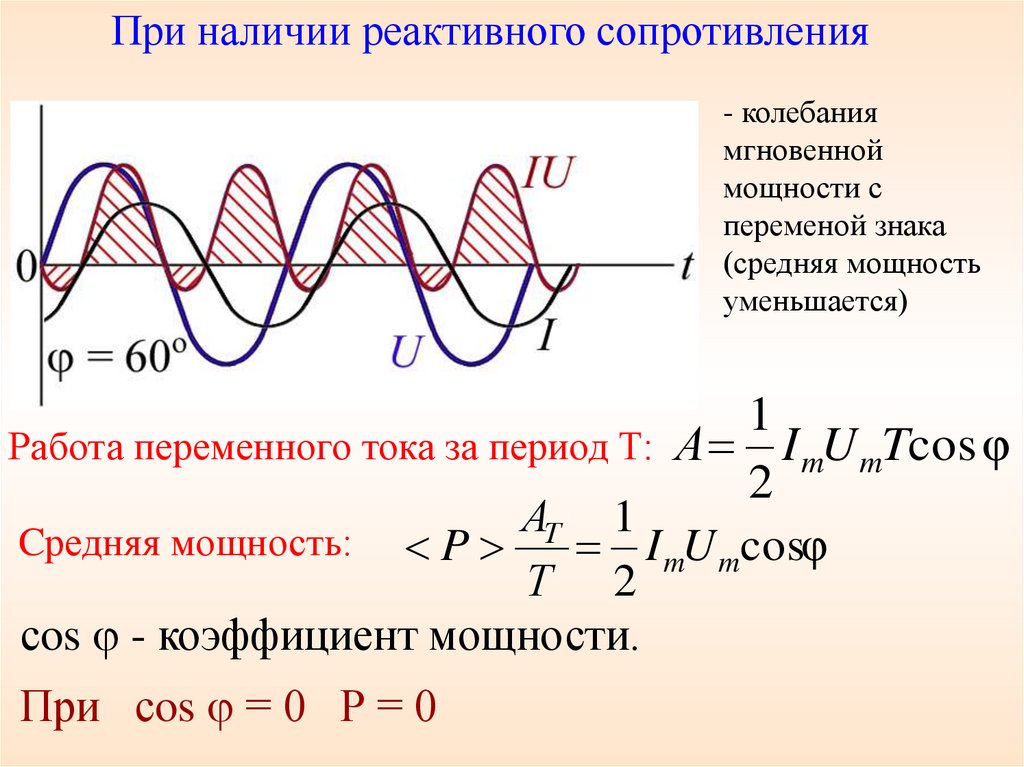
При наличии реактивного сопротивления- колебания
мгновенной
мощности с
переменой знака
(средняя мощность
уменьшается)
1
Работа переменного тока за период Т: А I mU mTcos φ
2
АТ 1
Cредняя мощность: P
I mU mcosφ
Т 2
сos - коэффициент мощности.
При сos = 0 Р = 0













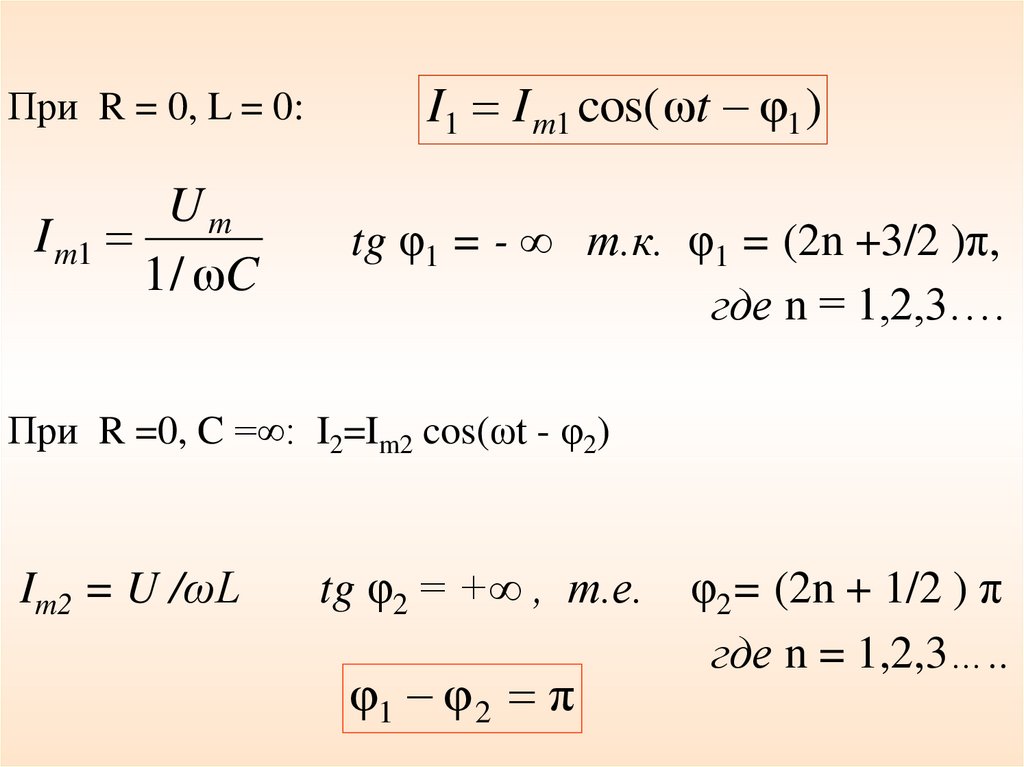








 physics
physics








