Similar presentations:
Электромагнитные колебания
1. С.Н. Охулков ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Федеральное агентство по образованиюНижегородский государственный технический университет
им. Р.Е. АЛЕКСЕЕВА
С.Н. Охулков
ЭЛЕКТРОТЕХНИКА
И ЭЛЕКТРОНИКА
Кафедра “Теоретическая и общая
электротехника”
Для студентов электротехнических
специальностей всех форм обучения
2.
Автозаводская высшая школа управления и технологийОчная и заочная форма обучения
- Автомобили и автомобильное хозяйство
- Автомобиле- и тракторостроение
- Технология машиностроения
г. Нижний Новгород, ул. Лескова, 68, т. (831) 256-02-10
3. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Тема 13ЭЛЕКТРОМАГНИТНЫЕ
КОЛЕБАНИЯ
27.06.2018
3
4. Колебания (колебательные движения)- изменения состояния, обладающие той или иной степенью повторяемости во времени.
Гармонические колебанияКолебания (колебательные движения)изменения состояния, обладающие той или
иной степенью повторяемости во времени.
Колебания могут иметь различную физическую
природу.
Колебания различают:
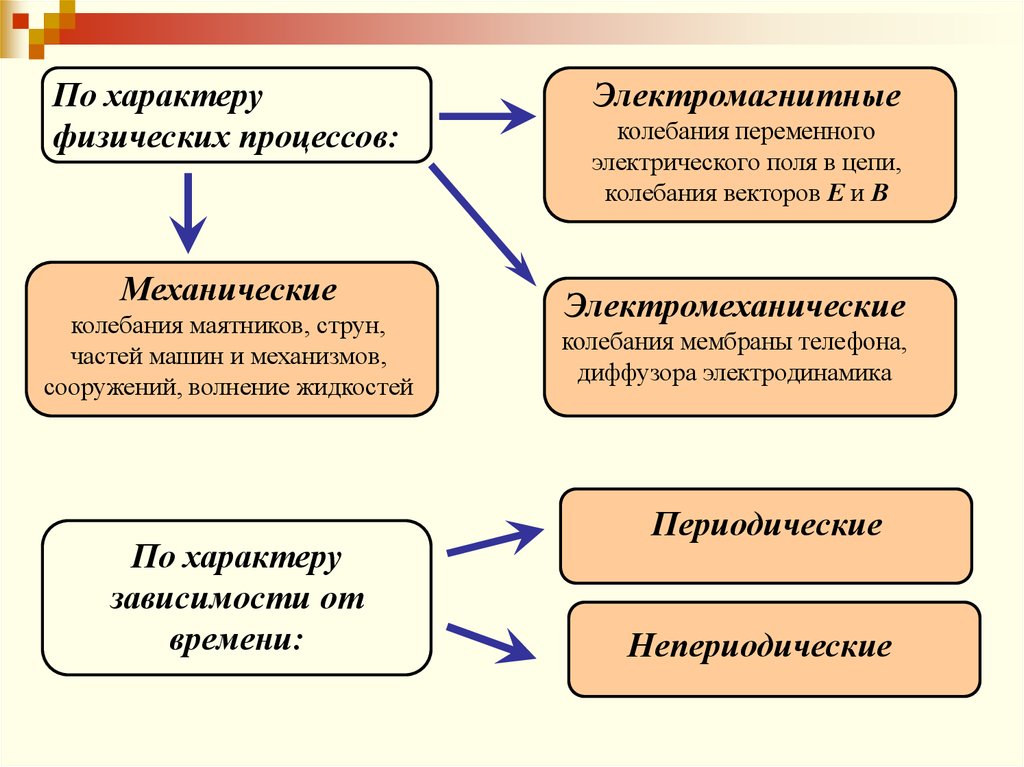
•по характеру физических процессов
•по характеру зависимости от времени.
5.
По характеруфизических процессов:
Механические
колебания маятников, струн,
частей машин и механизмов,
сооружений, волнение жидкостей
По характеру
зависимости от
времени:
Электромагнитные
колебания переменного
электрического поля в цепи,
колебания векторов Е и В
Электромеханические
колебания мембраны телефона,
диффузора электродинамика
Периодические
Непериодические
6.
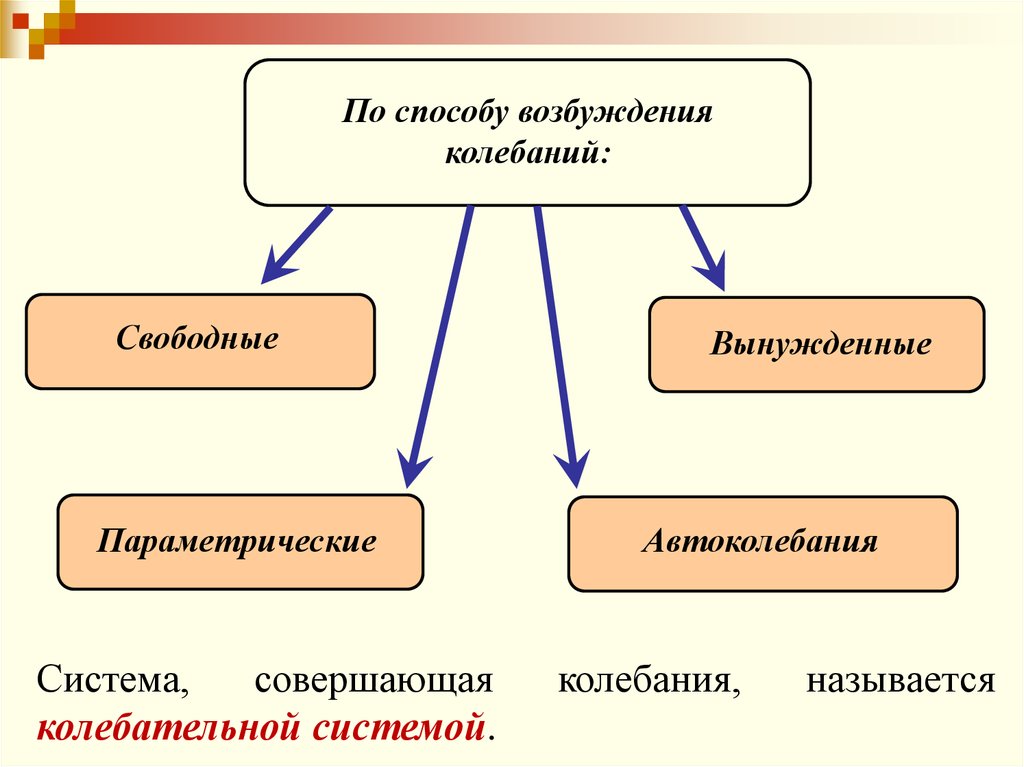
По способу возбужденияколебаний:
Свободные
Параметрические
Система,
совершающая
колебательной системой.
Вынужденные
Автоколебания
колебания,
называется
7.
Колебания называются периодическими, еслизначения физических величин, изменяющихся
в процессе колебаний, повторяются через
равные промежутки времени.
Периодические процессы можно представить
как наложение гармонических колебаний.
Гармонические колебания – колебания, при
которых колеблющаяся величина изменяется со
временем по закону синуса или косинуса.
8.
Периодом колебаний (Т) называетсянаименьший промежуток времени, через
который повторяются значения всех физических
величин, характеризующих колебательное
движение.
Частота периодических колебаний – число
полных колебаний, совершаемых в единицу
времени:
1
T
9.
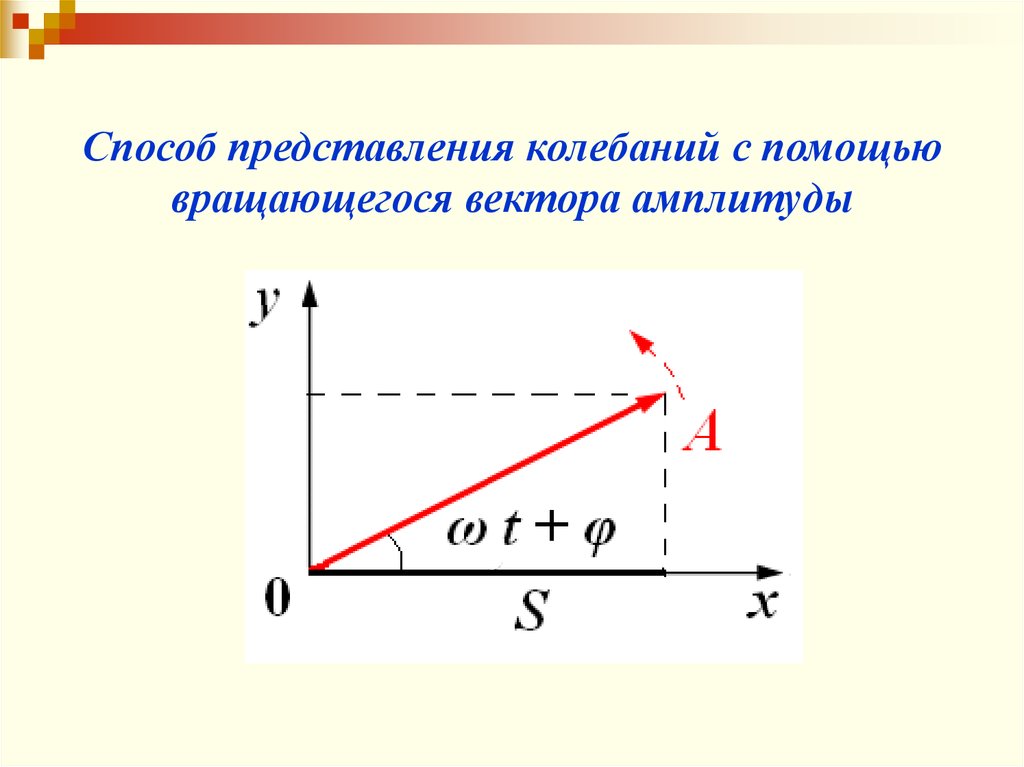
Способ представления колебаний с помощьювращающегося вектора амплитуды
10.
x A cos( ωt φ 0 )27.06.2018
x0 A cos φ 0
10
11.
Квазистационарные токи.Процессы в колебательном
контуре
Примером электрической цепи, в которой могут
происходить свободные электрические колебания,
служит простейший колебательный контур.
Для
простейшего
колебательного контура
R = 0.
11
27.06.2018
12.
Призамыкании
на
катушку
предварительно
заряженного конденсатора С в колебательном контуре
возникают свободные колебания заряда конденсатора и
тока в катушке. (R = 0)
Wэл .п.
27.06.2018
Q2
2C
Wм.п.
LQ 2
2
Wэл .п.
Q2
2C
Wм.п.
LQ 2
2
12
13.
Энергия электрического поляобкладками конденсатора С:
запасается
между
2
Q
Wэл.п.
.
2C
Энергия магнитного поля сосредоточена в катушке L:
2
2
LI
LQ
Wм.п.
.
2
2
Если R→ 0, тогда полная энергия:
2
Q
LQ
W
const.
2C
2
2
27.06.2018
13
14.
Переменноеэлектромагнитное
поле
распространяется в пространстве со скоростью
равной скорости света c = 3 · 108 м/с. Если l –
линейные размеры контура не велики (l ‹‹ c / ν, ν
– частота колебаний в контуре), то в каждый
момент времени сила тока во всех частях
контура одинакова. Такой переменный ток
называется квазистационарным.
27.06.2018
14
15.
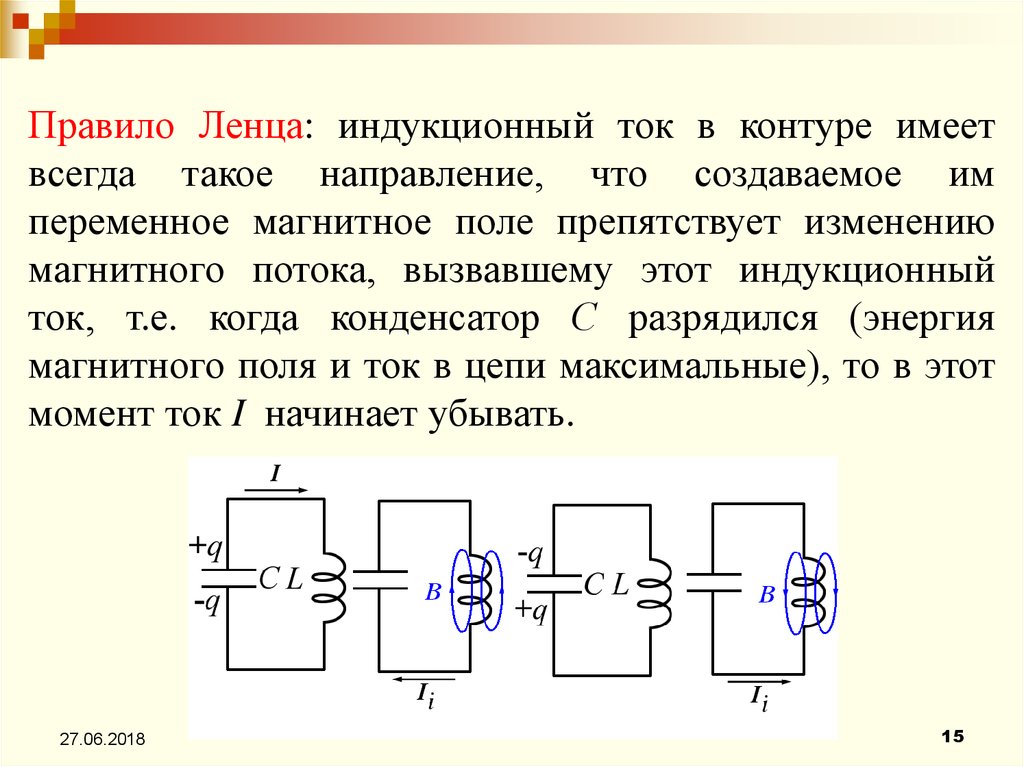
Правило Ленца: индукционный ток в контуре имеетвсегда такое направление, что создаваемое им
переменное магнитное поле препятствует изменению
магнитного потока, вызвавшему этот индукционный
ток, т.е. когда конденсатор С разрядился (энергия
магнитного поля и ток в цепи максимальные), то в этот
момент ток I начинает убывать.
27.06.2018
15
16.
Следовательно, магнитное поле в катушкеослабевает, и в катушке возникает индукционный ток Ii,
который препятствует уменьшению магнитного поля.
Направление
Ii совпадает с направлением
первоначального тока, и положительные заряды
продолжают идти в том же направлении, заряжая
положительно другую обкладку конденсатора С.
27.06.2018
16
17.
Закон Ома для контура:IR U C ES .
UR
Q
C
(1)
dI
L
dt
UC – разность потенциалов (напряжение) на обкладках
конденсатора С, Ɛs – э.д.с. самоиндукции.
Из закона сохранения заряда следует, что сила
квазистационарного тока
dQ
I
Уравнение (1):
27.06.2018
dt
Q.
dI
Q
L IR 0.
dt
C
17
18.
R1
Q Q
Q 0
L
LC
2
(2)
02
дифференциальное уравнение колебаний заряда Q в
контуре – дифференциальное уравнение затухающих
колебаний.
1
●R=0→
Q
Q 0
LC
дифференциальное
уравнение
колебаний.
гармонических
Свободные электрические колебания в колебательном
контуре являются гармоническими.
27.06.2018
18
19.
Уравнение гармонических колебаний:Q Qm cos 0t .
(3)
Qm – амплитуда заряда на конденсаторе С,
ω0 – собственная частота гармонических колебаний.
Из уравнения (2) следует
1
0
,
LC
2
T
2 LC
0
27.06.2018
- формула Томсона.
19
20.
I Q 0 Qm sin 0 t I m cos 0 t .2
(4)
Im
Qm
Im
LC
амплитуда тока.
Q Qm
UC
cos 0t U m cos 0t .
C
C
(5)
Um
Qm
Um
C
27.06.2018
-
амплитуда напряжения
20
21.
Из сопоставления электрических и механическихколебаний следует, что:
•энергия электрического поля аналогична
потенциальной энергии упругой деформации
•энергия
магнитного
поля
аналогична
кинетической энергии;
•Индуктивность L играет роль массы т
•1/С – роль коэффициента жесткости k
•Заряду q соответствует смещение маятника х
•Силе тока I ~ скорость υ
•Напряжению U ~ ускорение а
21
22.
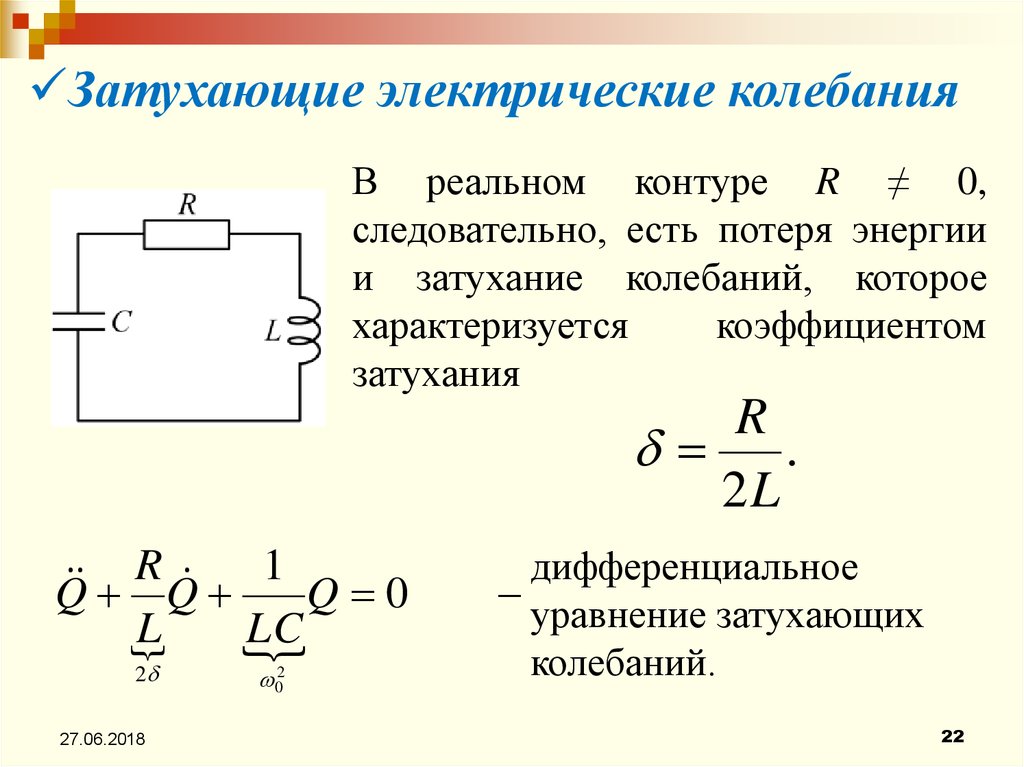
Затухающие электрические колебанияВ реальном контуре R ≠ 0,
следовательно, есть потеря энергии
и затухание колебаний, которое
характеризуется
коэффициентом
затухания
R
.
2L
R
1
Q Q
Q 0
L
LC
2
27.06.2018
02
дифференциальное
уравнение затухающих
колебаний.
22
23.
2 Q 2Q 0.Q
0
Решение дифференциального уравнения затухающих
колебаний:
t
Q Qm e
cos t ,
02 2
2
1
R
2
LC 4 L
- частота затухающих
колебаний.
При R = 0
27.06.2018
1
0 – собственной частоте контура.
LC
23
24.
Логарифмический декремент затухания:A(t )
ln
T .
A(t T )
Добротность колебательной системы:
0
W (t )
Q 2
W (t ) W (t T ) 2
1
1 L
.
R R C
LC
L
W(t) – энергия колебательной системы в момент
времени t,
W(t) – W(t+T)
– убыль энергии за промежуток
времени от t до T+ t.
24
25.
Вынужденные электрические колебаниявозникают в контуре при включении внешней э.д.с.
Закон Ома:
U U m cos t.
(1)
IR U С ES U .
(2)
Q
C
L
dI
dt
Um
R
1
Q Q
Q
cos t
L
LC
L
2
02
дифференциальное
колебаний.
27.06.2018
(3)
X0
уравнение
вынужденных
25
26.
При установившихся вынужденных колебаниях зарядконденсатора колеблется гармонически с циклической
частотой внешней э.д.с. – ω
Q Qm cos t ,
(4)
где α – сдвиг фаз между Q и внешней э.д.с.,
Qm
X0
2 2
Um
2
2
1
4
R
4
L
2 2 2
4L
LC
Um
Um
.
2
2
2
2
1
2
1
2
L 2 L
R L
2 R
C
C
L
L
02
2
2
(5)
26
27.
I Q Qm sin t Qm cos t .2
I
(6)
m
I m Qm .
(7)
Подставив уравнение (5) в уравнение (7), получим
Um
Im
. (8)
2
1
2
R L
C
1
Z R L
C
2
2
– полное сопротивление
цепи.
27
28.
Из уравнения для внешней э.д.с. (1) и уравнения (6)видно, что между током в контуре I и внешней э.д.с. U
есть сдвиг фаз
.
2
(9)
Решение дифференциального уравнения затухающих
колебаний дает
R
2
L
tg tg arctg 2
2
0 1 2
LC
R
R
L
. (10)
1
1
L
L
L C
C
28
27.06.2018
29.
Из уравнений (9), (10) следует1
L
1
C .
tg tg
2
tg
R
(11)
L
– реактивное индуктивное сопротивление,
1
C
– реактивное емкостное сопротивление.
1
Если L
, то φ > 0, т.е. ток I отстает по фазе от U,
C
1
если L
, то φ < 0, т.е. ток I опережает
C по фазе U.
27.06.2018
29
30.
Уравнение (2) запишем в виде:Q
dI
IR L U m cos t
(12)
C
dt
U R U C U L U m cos t. (13)
Сумма напряжений на отдельных элементах контура
равна в каждый момент времени внешней э.д.с.
U R RI RI m cos t RI m cos t . (14)
2
Q Qm
UC
cos t
U Cm cos t .
C
C
2
2
U
27.06.2018
Cm
(15)
30
31.
U CmQm
C
.
Um
Im
.
2
C
1
2
C R L
C
(16)
dI
U L L LI m sin t U Lm cos t .
dt
2
U
(17)
Lm
Сравнивая формулы для I, UR, UC, UL , можно сделать
вывод
UR изменяется в фазе с током I,
UC отстает от I, UR по фазе на
UL опережает I по фазе на
2
2
27.06.2018
31
32.
UФазовые
соотношения
представляются векторной
диаграммой
U
L
U U R UC U L .
φ
U
U
R
I
C
Резонансная частота для заряда Q и напряжения UC.
Q Uc рез
27.06.2018
2
1
R
02 2 2
2 0 .
LC 2 L
32
33.
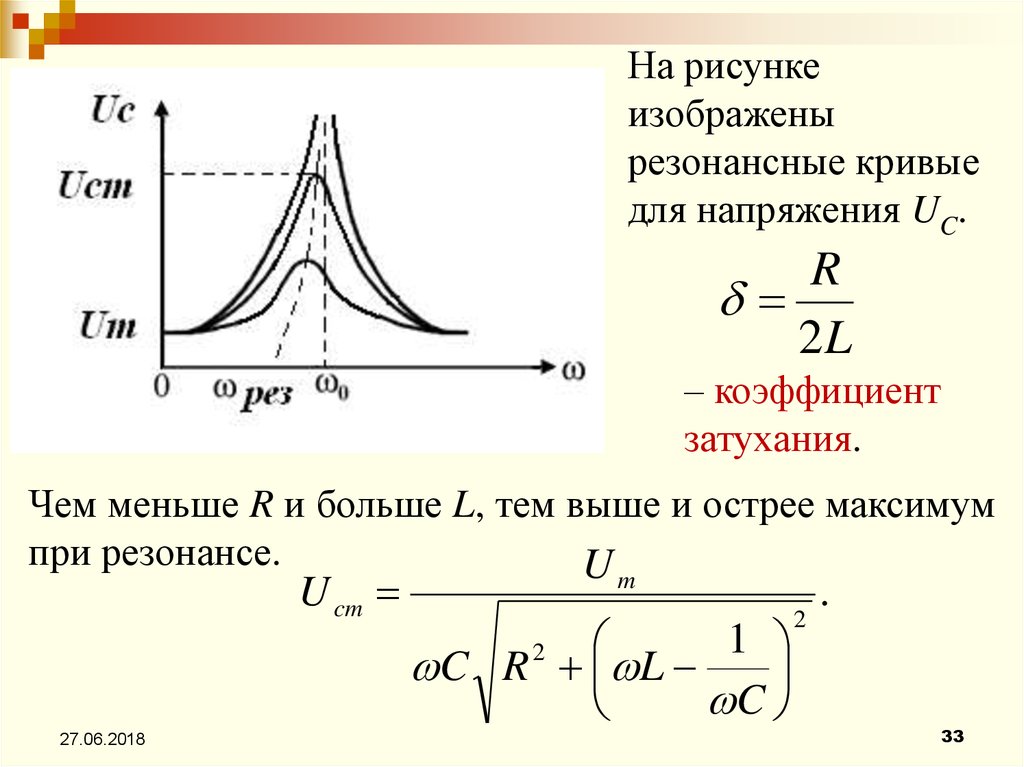
На рисункеизображены
резонансные кривые
для напряжения UC.
R
2L
– коэффициент
затухания.
Чем меньше R и больше L, тем выше и острее максимум
при резонансе.
U
U cm
m
1
C R L
C
2
.
2
27.06.2018
33
34.
Резонанс для тока возникает при1
L
0.
C
В этом случае угол сдвига фаз между током и
напряжением φ = 0 (tgφ = 0), изменение тока и
напряжения происходит синфазно.
I рез
27.06.2018
1
0 .
LC
34
35.
Полное сопротивлениецепи Z становится
минимальным (Z = R),
а
ток
становится
максимальным.
Im
Um
1
R L
C
2
2
0
Резонансные кривые для тока сходятся в 0, т.к. при
постоянном напряжении (ω = 0) ток в цепи,
содержащей конденсатор, не течет.
27.06.2018
35
.
36.
Ток в цепи определяется активным сопротивлением Rи принимает максимально возможное при данном Um
значение. При этом падение напряжения на активном
сопротивлении
равно
внешнему
напряжению,
приложенному к цепи UR = U, а падение напряжения на
конденсаторе
UС и катушке индуктивности UL
одинаковы по амплитуде и противоположны по фазе.
Это явление называется резонансом напряжений или
последовательным резонансом.
27.06.2018
36
37.
Явление резонанса напряжений используется в техникедля усиления колебания напряжения какой-либо
определённой частоты (для узкого интервала частот
вблизи
резонансной
частоты
контура
–
радиоприёмник).
Явление резонанса напряжений необходимо учитывать
при расчёте изоляции электрических цепей (линий),
содержащих C и L с целью предотвращения её пробоя.
27.06.2018
37
38.
Резонанс токов (параллельный резонанс)наблюдается в цепях переменного тока, содержащих
параллельно включенные конденсатор C и катушку
индуктивности L, при приближении частоты
приложенного напряжения к резонансной частоте
рез
1
.
LC
В этом случае разность фаз токов
IC и IL в параллельных ветвях
∆φ = π, т.е. токи в ветвях
противоположны по фазе, а амплитуда тока I = Im = ICm + ILm во
внешней (неразветвлённой) цепи равно нулю.
27.06.2018
38
39.
При активном сопротивлении цепей R ≠ 0 разность фазтоков ∆φ ≠ π амплитуда силы тока Im ≠ 0, но будет иметь
наименьшее возможное значение. Таким образом, при
резонансе токов токи IC и IL компенсируются, а сила
тока I в подводящих проводах достигает минимального
значения, обусловленного только током через R.
Может оказаться, что сила тока I << IC и IL.
Такой контур оказывает большое сопротивление
переменному току с частотой, близкой к ωрез.
Используется в резонансных усилителях; индукционных
печах, в которых C и L подбирают таким образом,
чтобы при частоте генератора сила тока через
нагревательную катушку была гораздо больше, чем
сила тока в подводящих проводах.
39
40.
Переменный токУстановившиеся вынужденные колебания можно
рассматривать как протекание в цепи, содержащей R, L,
C, переменного тока, обусловленного переменным
напряжением
U U m cos t. (1)
Этот ток изменяется по закону I I m cos t .
I m (U m , C , L, R, )
Um
1
R L
C
2
.
(2)
(3)
2
27.06.2018
40
41.
Ток I отстает по фазе от напряжения U на φ,определяемую выражением
1
L
C .
tg
R
(4)
Полное электрическое сопротивление (импеданс)
2
1
Z R L
.
C
2
27.06.2018
(5)
41
42.
Переменный ток, текущий через R .Закон Ома:
L → 0, C → 0
IR U U m cos t.
Um
Im
.
R
Следовательно, ток
изменяется в фазе с
напряжением и φ = 0.
Векторная диаграмма напряжения на сопротивлении:
27.06.2018
42
43.
.Переменный ток, текущий через L
Um
Im
,
L
tg
.
2
I L I m cos t ,
2
R → 0, C → 0
IL отстает от UL на
R L L
2
– реактивное индуктивное сопротивление.
Постоянному току (ω = 0) индуктивность не оказывает сопротивление.
43
44.
.Переменный ток, текущий через C
Um
Im
,
1
C
R → 0, L → 0
tg
.
27.06.2018
2
I C I m cos t ( ) ,
2
IC опережает UC на
1
RC
C
2
– реактивное емкостное сопротивление.
44
45.
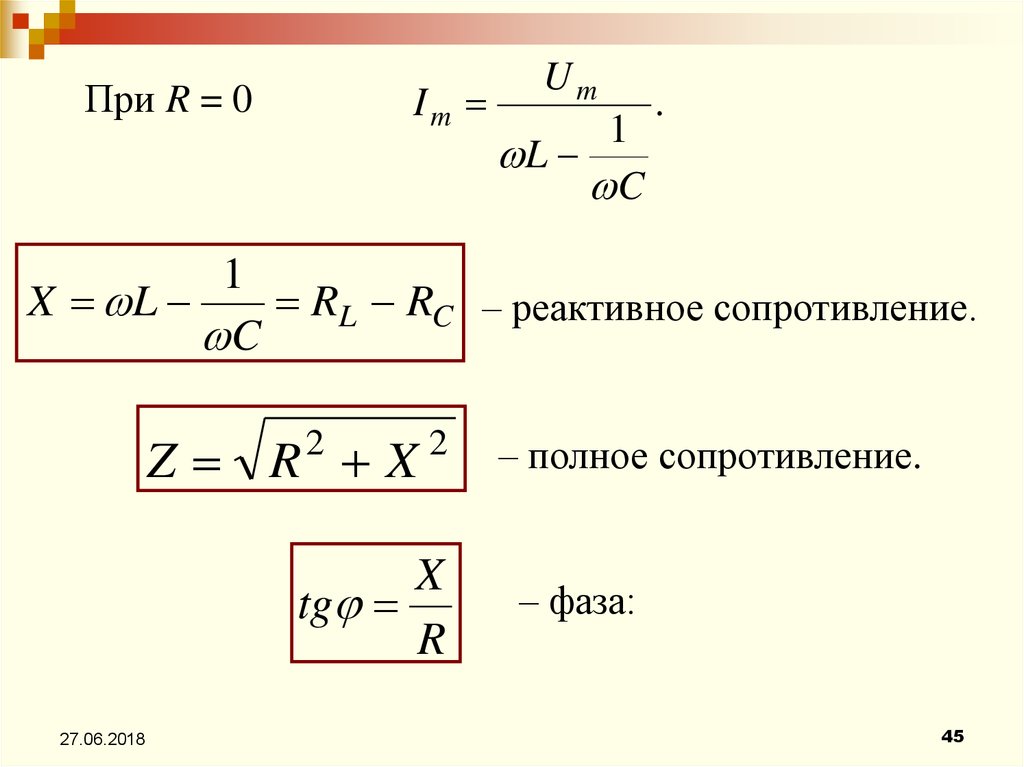
ImПри R = 0
Um
1
L
C
.
1
X L
RL RC – реактивное сопротивление.
C
Z R X
2
2
X
tg
R
27.06.2018
– полное сопротивление.
– фаза:
45
46.
Мгновенное значение мощности равно произведениюмгновенных значений U(t) и I(t)
P(t ) U (t ) I (t ) U m cos tI m cos t .
1
1
cos cos cos( ) cos( ).
2
2
1
1
P t U m I m cos U m I m cos 2 t .
2
2
сред. знач .
Среднее значение
27.06.2018
cos 2 t 0.
46
47.
Практическое значение представляет среднее значениемощности
1
P U m I m cos .
2
P(t) ~
cos 2 t ,
т.е. мгновенная мощность
колеблется около среднего
значения с частотой в 2
раза
превышающей
частоту тока.
27.06.2018
47
48.
Из векторной диаграммы видно, чтоU
U
L
UR I R R
cos
.
U
I
U
U
I Z Z
Подставляем это выражение в формулу для среднего
значения мощности:
RI m2
1 UmImR 1 Um
P
ImR
.
2 Z
2
Z
2
φ
R
C
Im
Такую же мощность развивает постоянный ток, сила
которого равна
Im
I
2
– действующее (эффективное)
значение силы тока.
48
49.
Аналогично,Um
U
2
– действующее значение
напряжения.
Уравнение средней мощности можно записать в виде:
Um Im
1
P U m I m cos
cos UI cos .
2
2 2
cos
называется коэффициент мощности.
В технике стремятся сделать cos максимальным.
Если cos мал, то для выделения в цепи требуемой
мощности надо иметь большой ток, что приводит к
росту потерь в проводах.
Для промышленных установок cos 0,85.
49
50. Рекомендуемая литература
1. Алтунин Б.Ю., Панкова Н.Г. Теоретические основы электротехники:Комплекс учебно - методических материалов: Часть 1 / Б.Ю. Алтунин,
Н.Г. Панкова; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-130 с.
2. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс
учебно-методических материалов: Ч.1/ Б.Ю. Алтунин, А.А. Кралин;
НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2007.-98 с.
3. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс
учебно-методических материалов: Ч.2/ Б.Ю. Алтунин, А.А. Кралин;
НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2008.-98 с
4. Касаткин, А.С. Электротехника /А.С. Касаткин, М.В. Немцов.-М.:
Энергоатомиздат, 2000.
5. Справочное пособие по основам электротехники и электроники
/под. ред. А.В. Нетушила.-М.: Энергоатомиздат, 1995.
6. Манаев Е.И. Основы радиоэлектроники.-3-е изд., перераб. И доп.-М.:
Радио и связь, 1990.-512 с.: ил.
7. Новожилов, О. П. Электротехника и электроника: учебник / О. П.
Новожилов. – М.: Гардарики, 2008. – 653 с.
Электротехника и электроника












































 physics
physics








