Гармонические колебания

1.

Гармонические колебания
1. Колебания подчиняющиеся
закону sin или cos
называются гармоническими
x1 A1 sin 0t 01
x2 A2 cos 0t 02
x смещение;
0
А амплитуда;
циклическк ая частота;
фаза колебаний ;
0 начальная фаза колебаний ;
x
A

2.

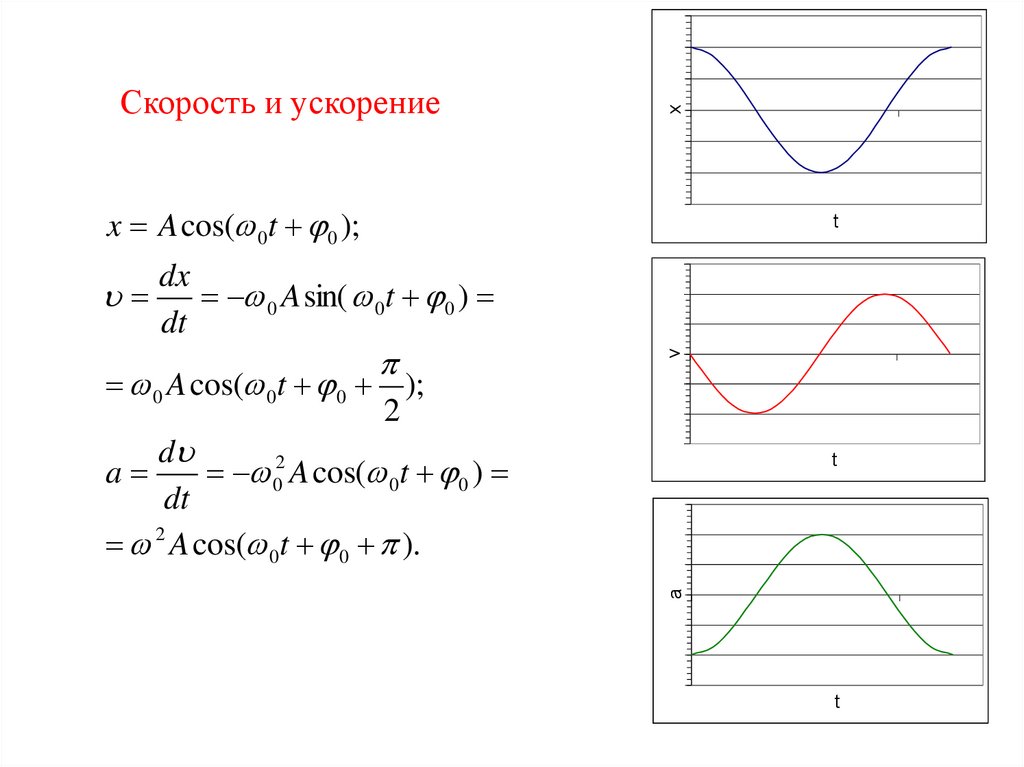
Скорость и ускорение
x A cos( 0t 0 );
dx
0 A sin( 0t 0 )
dt
0 A cos( 0t 0 );
2
d
a
02 A cos( 0t 0 )
dt
2 A cos( 0t 0 ).
0
x
A

3.

x
Скорость и ускорение
x A cos( 0t 0 );
t
v
dx
0 A sin( 0t 0 )
dt
0 A cos( 0t 0 );
2
d
a
02 A cos( 0t 0 )
dt
2 A cos( 0t 0 ).
a
t
t

4.

sin ; x l
Математический маятник
F mgtg mg
mgx
F
l
d 2x
mgx
F ma m 2
dt
l
d 2 x gx
g
2
0; замена 0
2
dt
l
l
d 2x
2
0 x 0.
2
dt
l
x A cos( 0t 0 ); T 2
g
T
F
x
mg

5.

Физический маятник
sin ; x l
M mgl sin J
d 2
J 2 mgl 0
dt
d 2 mgl
mgl
2
0; замена 0
2
dt
J
J
2
d 2
d
x
2
2
0
.
0
0 x 0.
2
2
dt
dt
J
x A cos( 0t 0 ); T 2
mgl
Атп
l
x
Oцм
mg

6.

Пружинный маятник
2
d x
F kx ma m 2
dt
2
d x
m 2 kx 0
dt
d 2 x kx
k
2
0; замена 0
2
dt
m
m
d 2x
2
0 x 0.
2
dt
x A cos( 0t 0 ); T 2
m
k

7.

СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
1. Сложение колебаний одинакового направления и частоты
x1 x m1 cos 0 t 01
+
x 2 x m 2 cos 0 t 02
x x m cos 0 t 0

8.

xm
2
02 01
2
2
x m1 x m 2 2x m1 x m 2 cos 2 1

9.

2 1
0 t 02 0 t 01
02 01
x m x m1 x m 2 2x m1 x m 2 cos 01 02
2
2
2
x sin 01 x m 2 sin 02
y y2
0 arctg 1
arctg m1
x1 x 2
x m1 cos 01 x m 2 cos 02

10.

2. Сложение колебаний одинакового направления с мало
отличающимися частотами
x1 x m cos 1t
x 2 x m cos 2 t
2 1
2 1
x 2 x m cos
t cos
t
2
2
2 1

11.

2 1
2 1
;
2
2
2 1
2
2
T
4
Tб
x 2 x m cos
t cos t
2

12.

3. Сложение взаимно перпендикулярных колебаний
одинаковой частоты
x x m cos 0 t
y y m cos 0 t
x 2 y2
2xy
2
cos
sin
2
2
x m ym x m ym

13.

1.
0:
ym
y
x;
xm
(прямая)
2.
:
ym
y
x
xm
3.
:
2
x 2 y2
2 1
2
x m ym
(прямая)
(эллипс)
При xm = ym - эллипс вырождается в окружность
При различных частотах складываемых колебаний
траектория результирующего колебания - фигуры
Лиссажу

14. Фигуры Лиссажу для случая A1=A2, w2¤w1=2/3 при различных значениях разности начальных фаз

Фигуры Лиссажу для случая A1=A2, w2¤w1=2/3 при
различных значениях разности начальных фаз

15. Фигуры Лиссажу для частных случаев сложения колебаний

16.

17.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Fсопр. r , r - коэффициент сопротивления
d2x
m 2 kx r x
dt
d 2 x dx
m 2 r kx 0
dt
dt
d2x
dx
m 2 kx r
dt
dt
d 2 x r dx k
x 0
2
dt
m dt m

18.

r
коэффициент затухания
2m
k
0
собственная частота
m
d 2 x r dx k
x 0
2
dt
m dt m
Решение :
x x m cos t 0
d2x
dx
2
2
0x 0
2
dt
dt
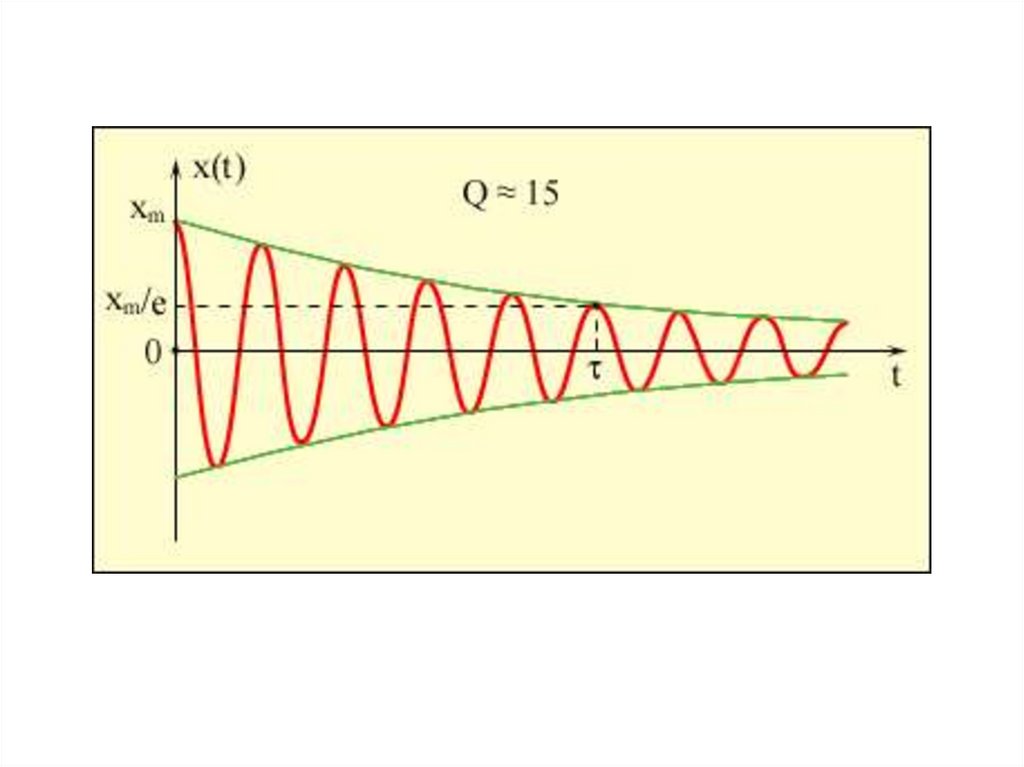
x x m 0 e t cos t 0
x m x m 0 e t
02 2

19.

Если 0 , то происходит апериодический процесс
возврата системы в состояние равновесия
Коэффициент затухания - величина, обратная времени,
за которое амплитуда колебаний уменьшается в е раз
Время релаксации - время, за которое амплитуда
уменьшается в е раз
1

20.

Логарифмический декремент затухания - величина,
обратная числу колебаний, за которое амплитуда
уменьшается в е раз
x m t
ln
x m t T
T
Добротность колебательной системы Q - величина,
пропорциональная числу колебаний, за которое
амплитуда уменьшается в е раз
Q

21.

22.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
F Fm cos t
d2x
m 2 kx r x Fmx cos t
dt
d2x
m 2 kx r x Fmx cos t
dt
d2x
dx
Fmx
2
2
x
cos t
0
2
dt
dt
m

23.

d2x
dx
Fmx
2
2
x
cos t
0
2
dt
dt
m
x x m cos t 0
Fmx
xm
m ( 02 2 ) 4 2 2
2
0 arctg 2
2
0
рез. 02 2 2

24.

1 0
2 3 4