Гармонические колебания. Колебательные процессы

1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

2. 1. КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ

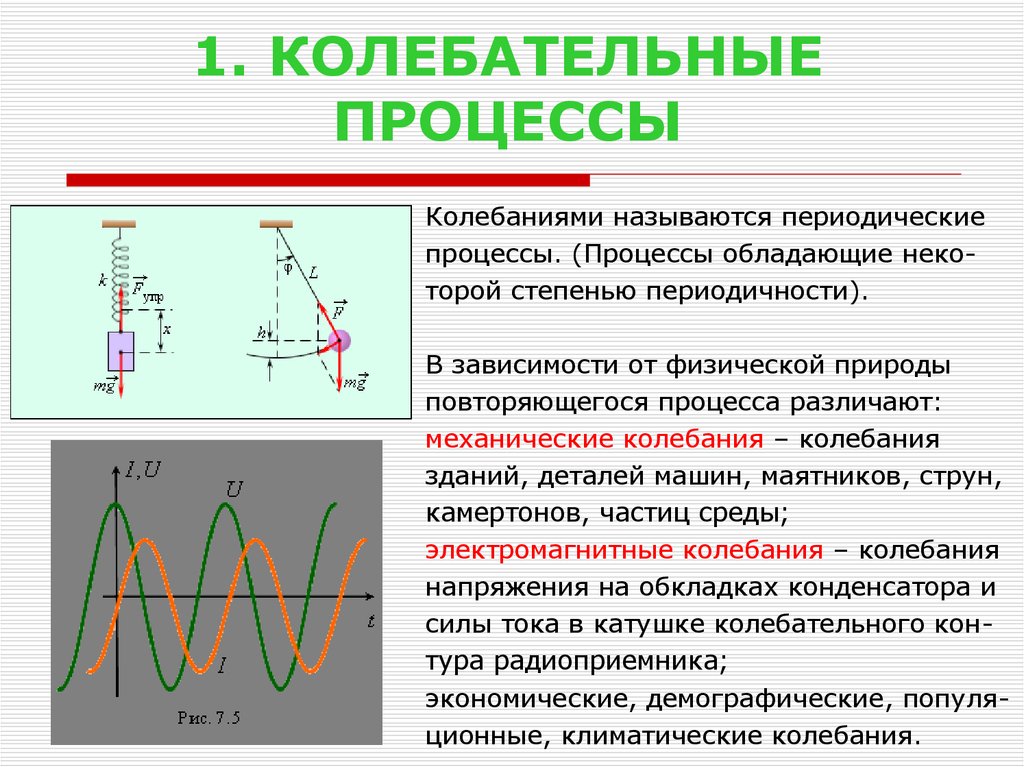
Колебаниями называются периодические
процессы. (Процессы обладающие некоторой степенью периодичности).
В зависимости от физической природы
повторяющегося процесса различают:
механические колебания – колебания
зданий, деталей машин, маятников, струн,
камертонов, частиц среды;
электромагнитные колебания – колебания
напряжения на обкладках конденсатора и
силы тока в катушке колебательного контура радиоприемника;
экономические, демографические, популяционные, климатические колебания.

3. 2. КЛАССИФИКАЦИЯ КОЛЕБАНИЙ

В зависимости от характера воздействия на колеблющуюся систему
различают свободные (собственные)
колебания, вынужденные колебания,
автоколебания и параметрические
колебания.
Свободными (или собственными), называются колебания, которые происходят в системе, предоставленной
самой себе после того, как она была
выведена из положения равновесия.
Вынужденными называются колебания,
в процессе которых колеблющаяся
система подвергается воздействию
внешней периодической силы.

4. 3. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

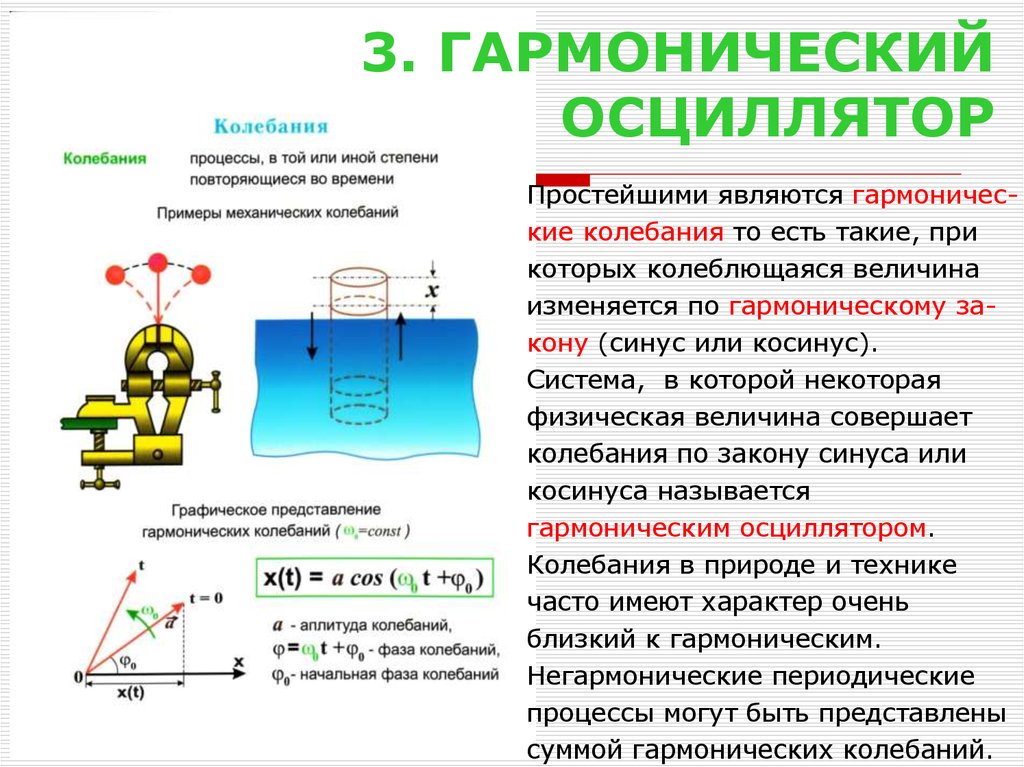
Простейшими являются гармонические колебания то есть такие, при
которых колеблющаяся величина
изменяется по гармоническому закону (синус или косинус).
Система, в которой некоторая
физическая величина совершает
колебания по закону синуса или
косинуса называется
гармоническим осциллятором.
Колебания в природе и технике
часто имеют характер очень
близкий к гармоническим.
Негармонические периодические
процессы могут быть представлены
суммой гармонических колебаний.

5. 4. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ

Рассмотрим колебания гармонического осциллятора.
Они описываются уравнением
max Fx ;
ax Vx x;
Fx kx mx kx
k
mx kx 0 x x 0;
m
k
2
2
x
0
0 x 0.
m
x(t ) a cos( 0t 0 ).

6. 5. ПАРАМЕТРЫ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

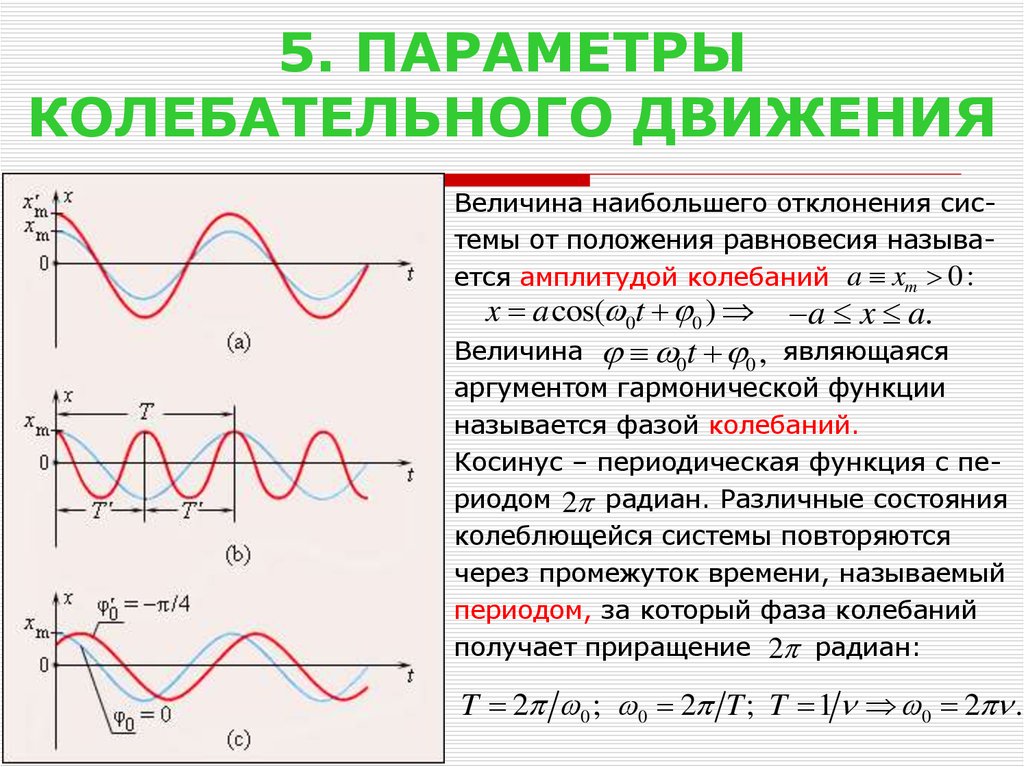
Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебаний a xm 0 :
x a cos( 0t 0 ) a x a.
Величина 0t 0 , являющаяся
аргументом гармонической функции
называется фазой колебаний.
Косинус – периодическая функция с периодом 2 радиан. Различные состояния
колеблющейся системы повторяются
через промежуток времени, называемый
периодом, за который фаза колебаний
получает приращение 2 радиан:
T 2 0 ; 0 2 T ; T 1 0 2 .

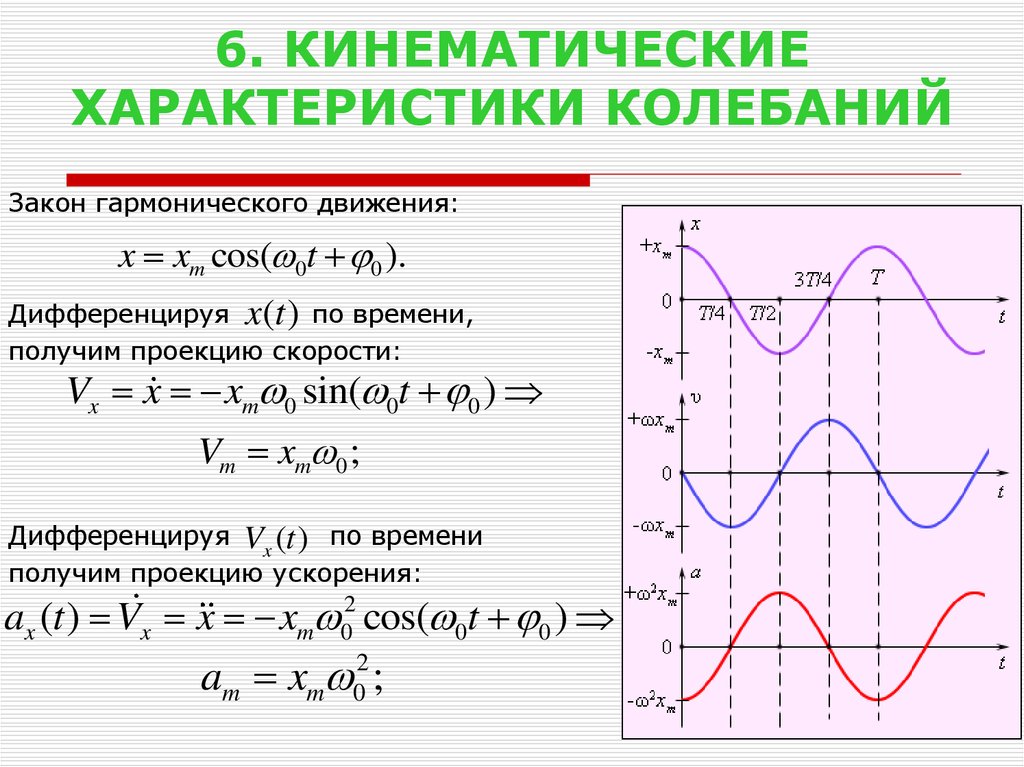
7. 6. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОЛЕБАНИЙ

Закон гармонического движения:
x xm cos( 0t 0 ).
Дифференцируя x(t ) по времени,
получим проекцию скорости:
Vx x xm 0 sin( 0t 0 )
Vm xm 0 ;
Дифференцируя Vx (t ) по времени
получим проекцию ускорения:
ax (t ) Vx x xm 02 cos( 0t 0 )
am xm ;
2
0

8. 7. ЭНЕРГИЯ КОЛЕБАНИЙ

Квазиупругая сила F kx является консервативной. Ей отвечает
x
потенциальная энергия U ( x) kx 2 2, полная энергия гармонических
колебаний должна оставаться неизменной.
E U m Km ; U m kxm2 2; K m mVm2 2;
U m K m kxm2 mVm2 ; k m 02
m x mV
2 2
0 m
2
m
Vm2 ( xm 0 )2 Vm xm 0 .
U (t ) U m 2 U m 2cos(2 0t 2 0 );
K (t ) Km 2 K m 2cos(2 0t 2 0 );
K (t ) U (t ) E K m U m .

9. 8. ПРУЖИННЫЙ МАЯТНИК

Маятником называют тело, совершающее колебания под
действием силы тяжести.
Рассмотрим систему, состоящую из тела массой m,
подвешенного на пружине, массой которой можно
пренебречь.
В положении равновесия сила тяжести
уравновешивается упругой силой mg kx0 .
Будем характеризовать смещение шарика из положения равновесия координатой
причем ось
направим вертикально вниз, а нуль оси совместим
с положением равновесия шарика.
Если сместить шарик в положение, характеризуемое координатой
то
удлинение пружины станет равным
а проекция результирующей
0
силы примет значение F mg k ( x x) mg kx kx F kx.
x
x,
x,
x x,
x
0
0
k x
max Fx mx kx
mx kx 0 x x 0
m
k
;
x xm cos( 0t 0 ); 0
T 2 0 2 m k .
m

10. 9. МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ

Физический маятник – любое твердое тело, совершающее
малые колебания относительно оси, не проходящей через его
центр масс.
m cos( 0t 0 ).

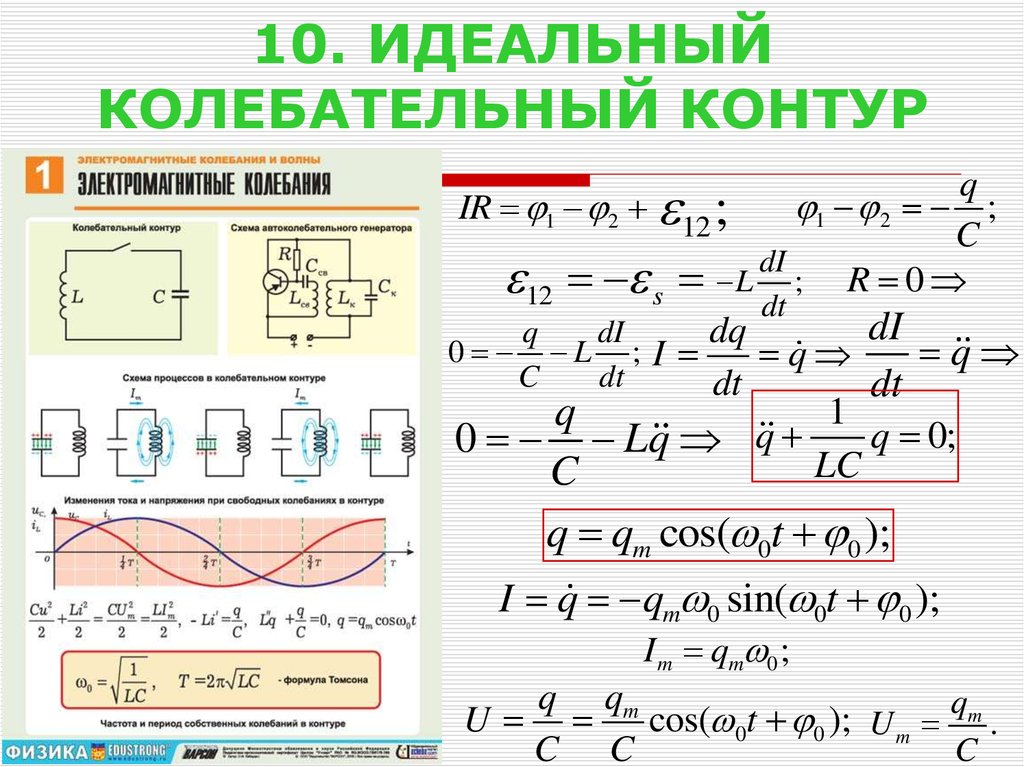
11. 10. ИДЕАЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

q
1 2 ;
IR 1 2 ;
12
C
dI
12 s L dt ; R 0
dI
dq
q
dI
0 L ; I
q
q
C
dt
dt
dt
1
q
q 0;
0 Lq q
LC
C
q qm cos( 0t 0 );
I q qm 0 sin( 0t 0 );
I m qm 0 ;
q qm
q
U
cos( 0t 0 ); U m m .
C C
C