Механические гармонические колебания. §1. Колебательное движение. Признаки и условия колебательного движения

1.

Тема: Механические
гармонические колебания

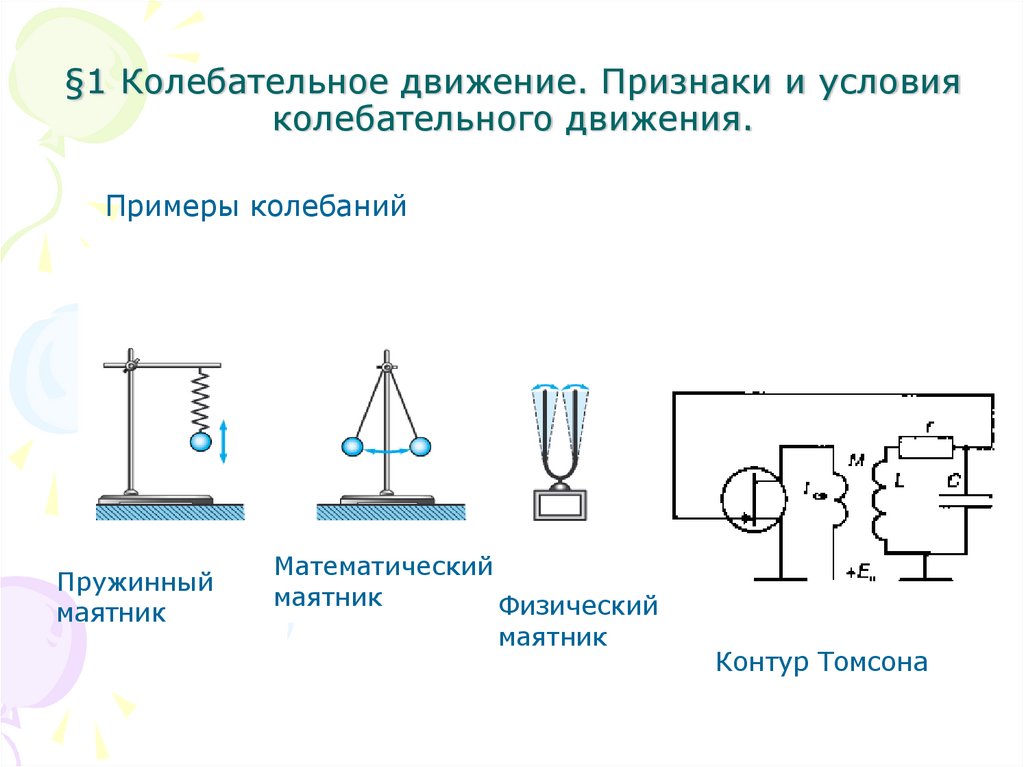
2. §1 Колебательное движение. Признаки и условия колебательного движения.

Примеры колебаний
Пружинный
маятник
Математический
маятник
Физический
маятник
Контур Томсона

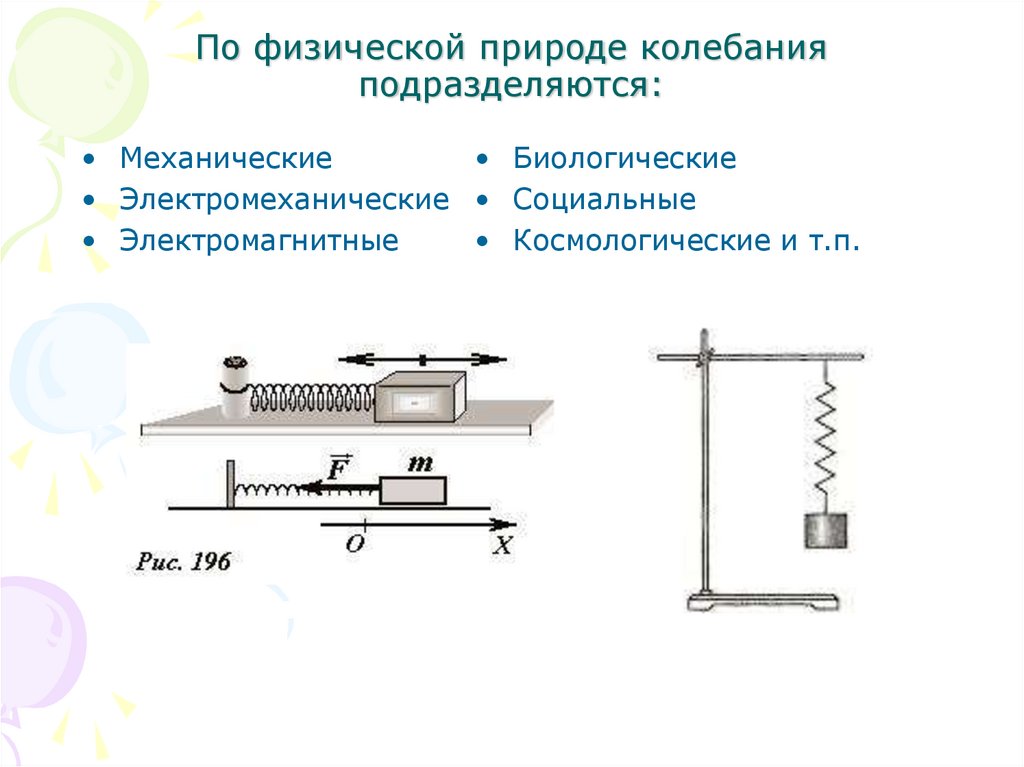
3. По физической природе колебания подразделяются:

• Механические
• Биологические
• Электромеханические • Социальные
• Электромагнитные
• Космологические и т.п.

4. Признаки колебания:

• Наличие равновесного состояния в системе.
• Непрерывная изменяемость скорости V и силы F по
величине и направлению.
• Главный признак – повторяемость движения.
Итак: колебательное движение (процесс) – всякое
изменение состояния системы, характеризуемое той или
иной степенью повторяемости во времени физических
величин, которые определяют это движение или
состояние.

5. Условия колебательного движения:

• Наличие Fупр (или Fквазиупр) силы, направленной к
положению равновесия (возвращающая сила).
• Система должна обладать инерцией.
Наиболее простой вид колебания – гармонический. Это
означает: F ~ У и изменение характеристик движения
происходит по закону sin и cos.
В зависимости от силового внешнего воздействия
колебания бывают:
• Свободные (собственные), незатухающие;
• Затухающие (есть Fсопротив);
• Вынужденные (Fвынужд ).

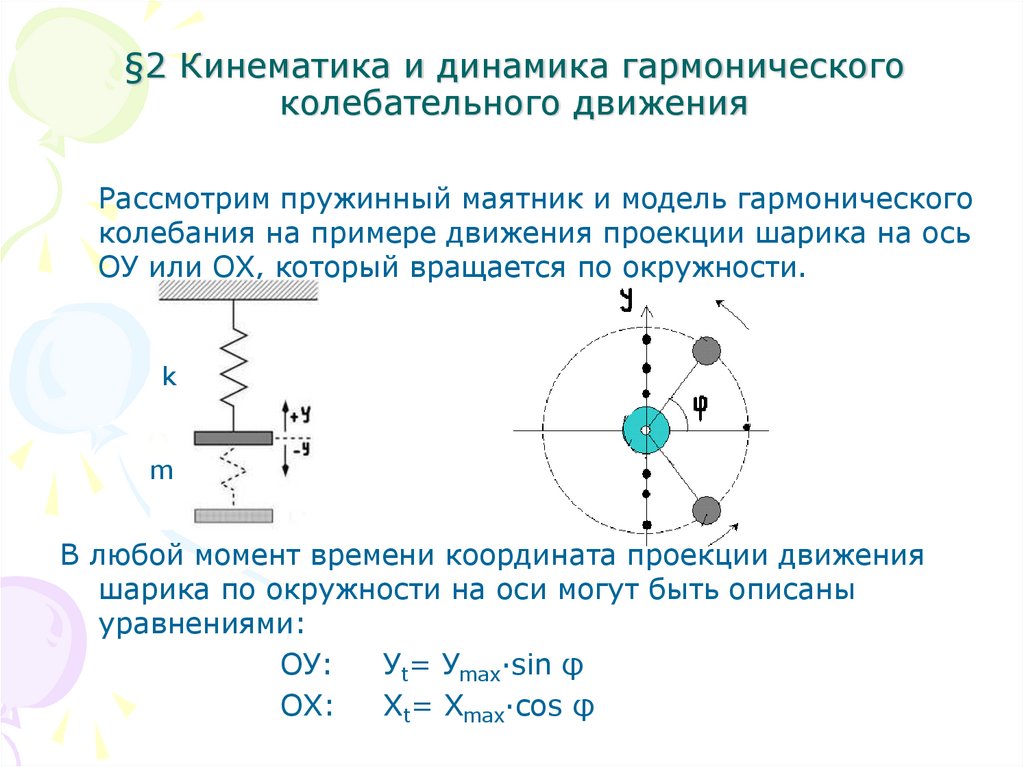
6. §2 Кинематика и динамика гармонического колебательного движения

Рассмотрим пружинный маятник и модель гармонического
колебания на примере движения проекции шарика на ось
ОУ или ОХ, который вращается по окружности.
k
m
В любой момент времени координата проекции движения
шарика по окружности на оси могут быть описаны
уравнениями:
OУ:
Уt= Уmax·sin φ
OX:
Xt= Xmax·cos φ

7.

Эти выражения являются уравнениями гармонического
движения. Их вывод можно осуществить на основе
анализа динамики колебания тела. Для пружинного
маятника возвращающую силу можно выразить:
Fупр= -к·У (по закону Гука)
(1)
Fупр= m·a (по 2-му закону Ньютона)
(2)
Из уравнений (1) и (2) получаем: -к·У = m·a
или a ky
- уравнение динамики, а~у
(3)
(4)
m
2
d
y , то уравнение (4) выразим, как:
Если учесть, что: a
dt 2
d2y
d2y
k
k
y
y 0
2
2
dt
m
m
dt
Это дифференциальное уравнение гармонического
колебания 2-го порядка.
(5)

8.

Решение этого дифференциального уравнения имеет вид:
y A sin( 0 t 0 )
(6)
– это уравнение описывает кинематику гармонического
движения,
где ω0 -собственная частота колеблющейся системы, которая
определяется коэффициентом упругости (k) и массой (m)
колеблющегося тела
k
0
m
2
0
k
m
(7)
Из уравнения (6) можно получить уравнения для скорости и
ускорения:
dy
A 0 cos( 0 t 0 )
dt
dV
a
A 02 sin( 0t 0 )
dt
V
(8)
(9)
Любая физическая система, совершающая гармонические
колебания, называется гармоническим осциллятором.

9. Кинематические характеристики колебания:

У (или Х) – смещение – это линейное отклонение точки от положения
равновесия;
• А=Уmax – амплитуда – это максимальное смещение;
• ω0 – круговая(циклическая) частота
2
0
2
(10),
Т
где
- линейная частота, Гц
• Т – период – время одного полного колебания, сек
для пружинного маятника:
(11)
m
v
Т 2
k
φ0 – начальная фаза (угловое смещение в момент времени t=0)
( 0 t 0 )
– фаза колебания – угловой путь за время t, рад
Графическое изображение гармонического колебания

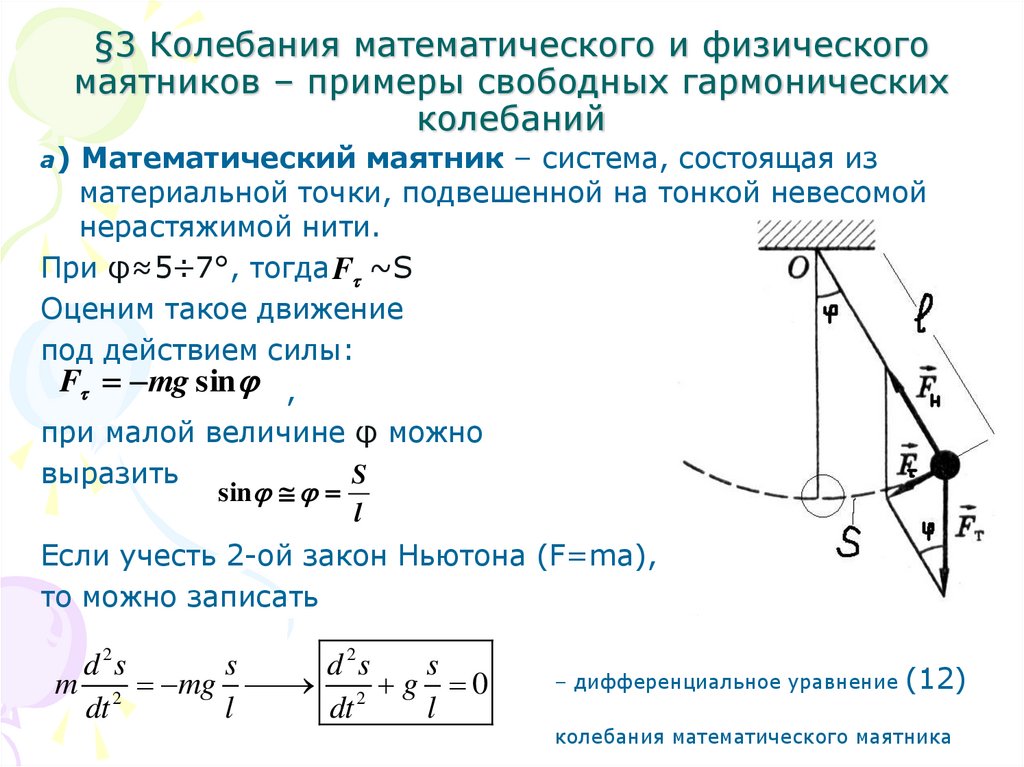
10. §3 Колебания математического и физического маятников – примеры свободных гармонических колебаний

а) Математический маятник – система, состоящая из
материальной точки, подвешенной на тонкой невесомой
нерастяжимой нити.
При φ≈5÷7°, тогда F ~S
Оценим такое движение
под действием силы:
F mg sin ,
при малой величине φ можно
выразить
S
sin
l
Если учесть 2-ой закон Ньютона (F=ma),
то можно записать
d 2s
s
d 2s
s
m 2 mg
2 g 0
dt
l
dt
l
– дифференциальное уравнение (12)
колебания математического маятника

11.

Решением уравнения (12) будет выражение:
S S0 sin 0t
Таким образом, уравнение (13) указывает, что движение
гармоническое, подчиняющееся закону sin.
Из уравнения (12) следует:
g
l
0
(14),
T 2
l
g
(13)
(15)
б) Физический маятник – система, состоящая из твердого тела,
которое может колебаться около горизонтальной оси, не проходящей
через центр тяжести, под действием момента силы тяжести.
(φ≈5÷7°)
Физический маятник колеблется под действием момента
тангенциальной составляющей силы тяжести:
F mg sin mg mg
S
l
Т.к. колеблется твердое тело, то надо принять
M F L
где L – плечо относительно оси колебания
S
M mg L
mgS
L
(16)

12.

Момент силы М определяет по 2-му закону Ньютона угловое ускорение–ε,
2
2
2
d
d
mgS
1
d
S mgS
M
0
2
2
2
т.е. (17), но
dt
dt
J
L dt
J
J
далее:
d 2 S mgSL
0 – дифференциальное уравнение
2
dt
J
Решением будет:
это гармоническое движение
S S0 sin 0t
mgL
Из уравнения (19) имеем:
02 => 0
J
J
T 2
mgL
mgL
J
– период физического маятника
(18)
(19)
(20)
(21)
(22)

13. §4 Энергия гармонического колебания

Полная механическая энергия при гармоническом колебании в общем
случае состоит из кинетической и потенциальной:
mV 2 ky 2
W мех W K W П
2
2
(24)
mA2 02 cos 2 ( 0t 0 ) A2 sin 2 ( 0t 0 )
Wмех
2
2
mA2 02
mA2 02
2
2
cos 0t 0 sin 0t 0
2
2
В любой момент времени энергия не изменяется:
mA2 02
A2
Wмех
2
2
В крайних положениях
(25)
W мех W П , а в положении равновесия W мех W К

14.

Wк
Wп
Колебательная система – консервативная система!
Из формулы (25) можно оценить влияние частоты ω0 на
амплитуду А.
Например, имеем две системы с энергией W1= W2=W:
2
2
m 2 A22 02
m1 A12 01
и
W
W1
2
2
2
A1
02
A2
01 , т.е.
Если принять, что m1= m2 и W1= W2, то
соотношение амплитуд обратно пропорционально
соотношению частот