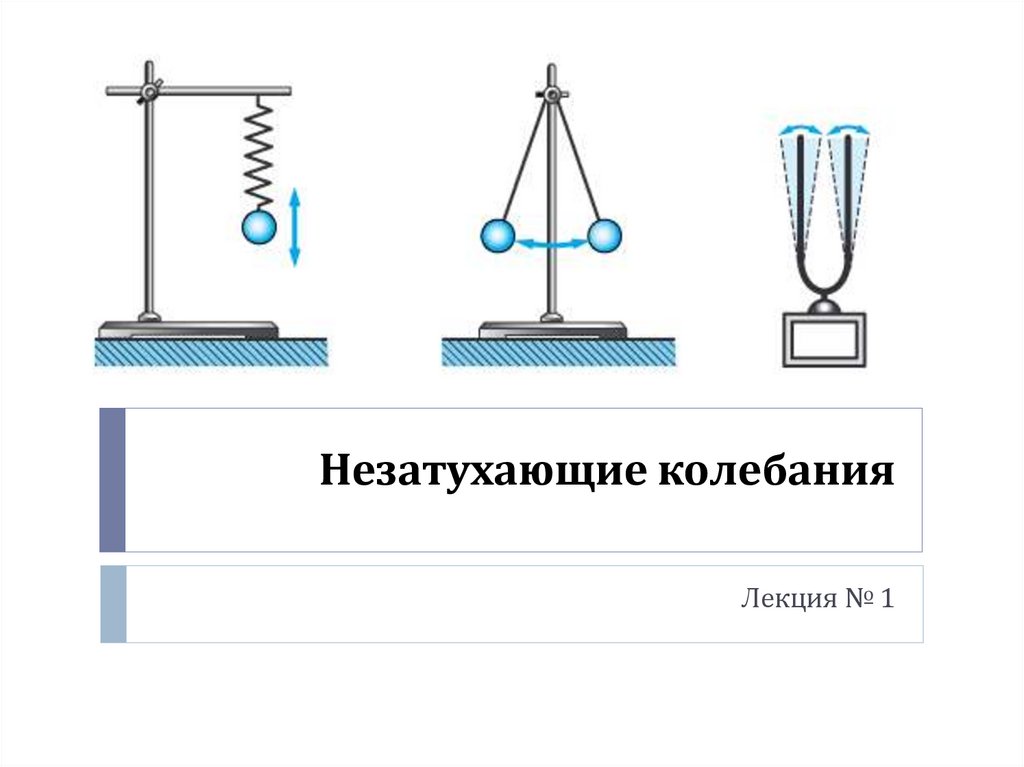
Незатухающие колебания. Лекция № 1

1. Незатухающие колебания

Лекция № 1

2. План лекции:

1.
2.
3.
4.
Гармонические колебания и их характеристики.
Механические гармонические колебания.
Гармонический осциллятор. Пружинный,
физический и математический маятники.
Свободные гармонические колебания в
колебательном контуре.

3. 1. Гармонические колебания и их характеристики

Колебаниями называются движения или процессы,
обладающие той или иной повторяемостью во
времени.

4. В зависимости от физической природы, колебания подразделяют на:

механические,
электромеханические,
электромагнитные и т. д.

5. 1. Гармонические колебания и их характеристики

Колебания называются свободными (или
собственными), если они совершаются за счет
первоначально сообщенной энергии при
последующем отсутствии внешних воздействий на
колебательную систему (систему, совершающую
колебания).
Гармонические колебания колебания, при которых
колеблющаяся величина изменяется со временем по
закону синуса (косинуса).

6. 1. Гармонические колебания и их характеристики

Гармонические колебания величины s описываются
уравнением:
s A cos 0t
s A sin 0t
где s – отклонение или смещение колеблющейся величины
от положения равновесия;
A – амплитуда, т. е. наибольшее отклонение от
положения равновесия;
(ω0t + ) – фаза колебания;
– начальная фаза, т. е. значение фазы в начальный
момент времени;
ω0 – круговая, или циклическая частота.

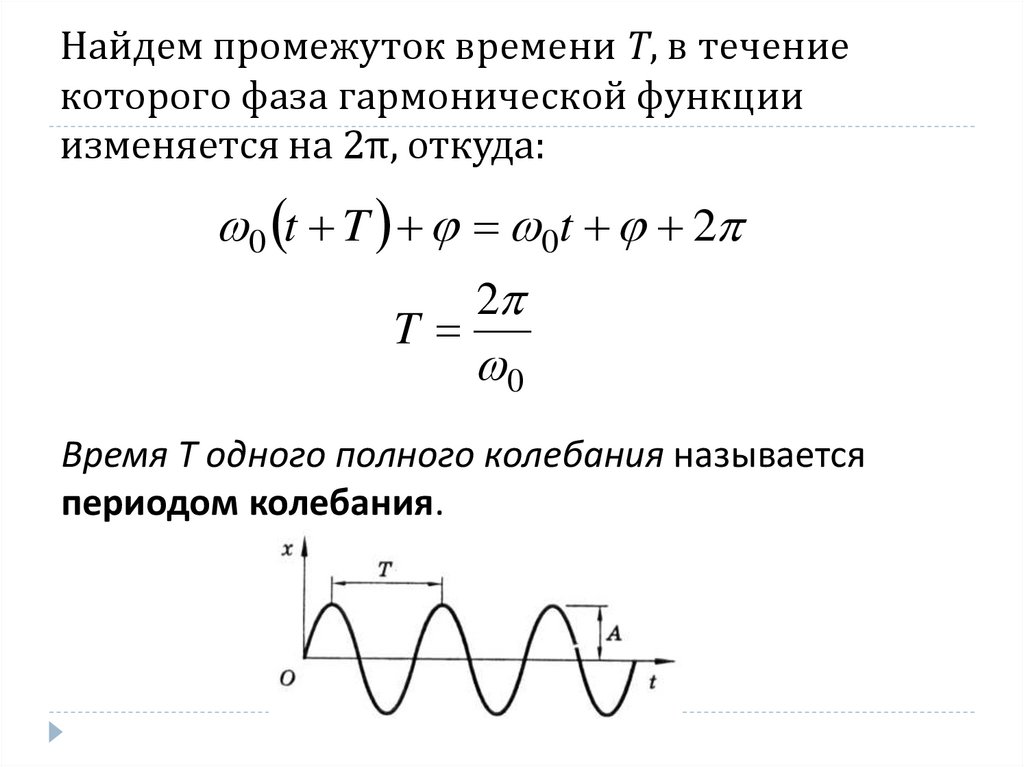
7. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π, откуда:

0 t T 0t 2
2
T
0
Время T одного полного колебания называется
периодом колебания.

8. Частотой ν называют число колебаний в единицу времени, т. е. величину, обратную периоду:

Частотой ν называют число колебаний в
единицу времени, т. е. величину, обратную
периоду:
Единица измерения частоты – герц (Гц): 1 Гц частота
периодического процесса, при которой за 1 с
совершается один цикл процесса.
0 2

9. 1. Гармонические колебания и их характеристики

Дифференциальное уравнение гармонических
колебаний:
2
d s
2
s
0
0
2
dt
Решение этого уравнения:
s A cos 0t

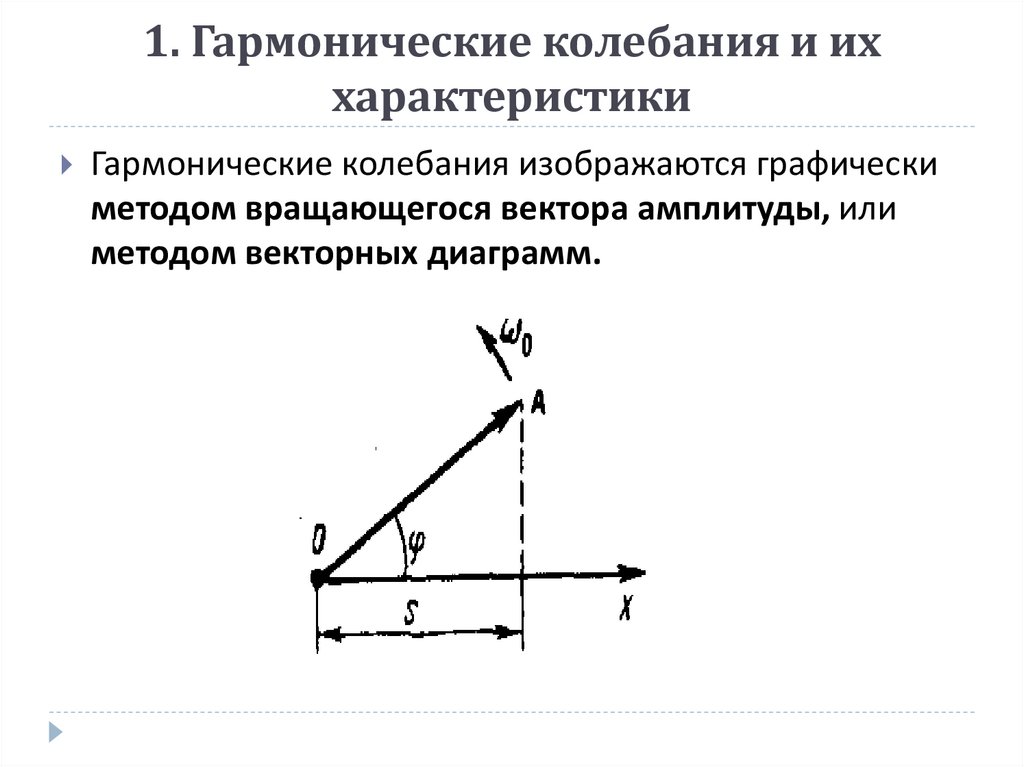
10. 1. Гармонические колебания и их характеристики

Гармонические колебания изображаются графически
методом вращающегося вектора амплитуды, или
методом векторных диаграмм.

11. 2. Механические гармонические колебания

Зависимость координаты х от времени t задается
уравнением:
x A cos 0t
Скорость υ и ускорение а колеблющейся точки:
A 0 sin 0t A 0 cos 0t
2
a A 02 cos 0t A 02 cos 0t

12. 2. Механические гармонические колебания

Сила
F ma , действующая на колеблющуюся
материальную точку массой т, равна
2
F m 0 x
Гармоническим называется колебание, вызываемое
силой, пропорциональной смещению и направленной
против смещения.
Сила, которая стремится возвратить точку в
положение равновесия, называется возвращающей
силой.

13. 2. Механические гармонические колебания

Кинетическая энергия материальной точки
m
T
2
2
2
mA 0
2
2
sin 0t
2

14. 2. Механические гармонические колебания

Потенциальная энергия материальной точки:
x
2 2
m 0 x
0
2
П Fdx
2
mA 0
2
2
Полная энергия:
E T П
2
mA 0
2
2
cos2 0t

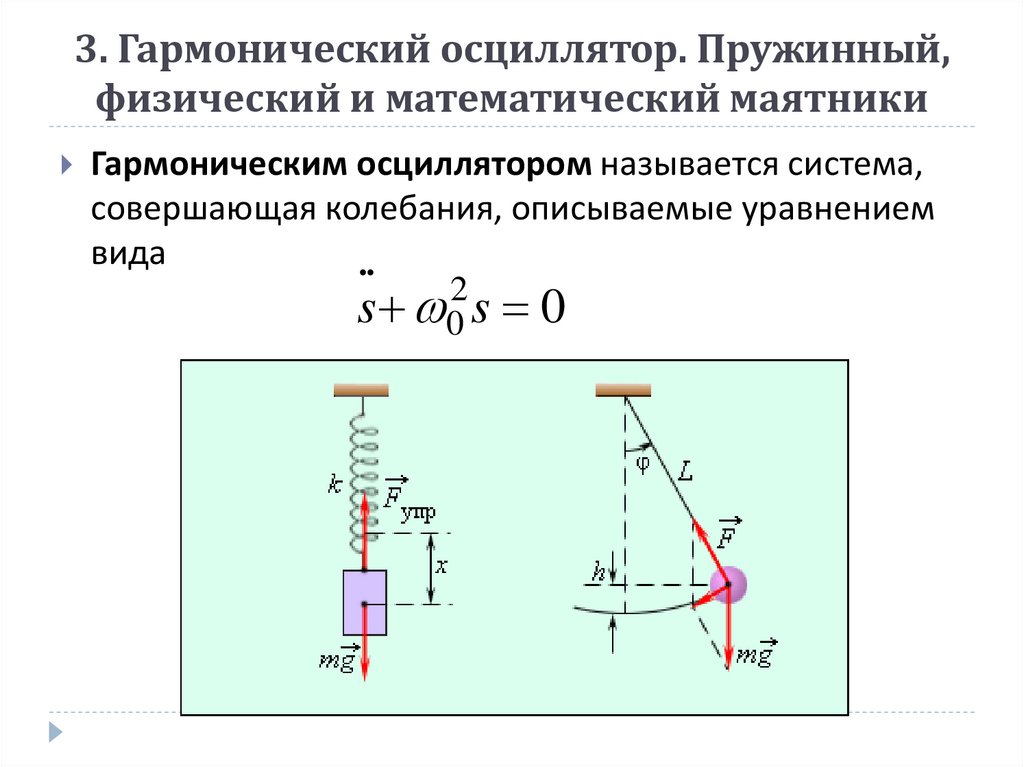
15. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

Гармоническим осциллятором называется система,
совершающая колебания, описываемые уравнением
вида
..
2
s 0 s 0

16. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

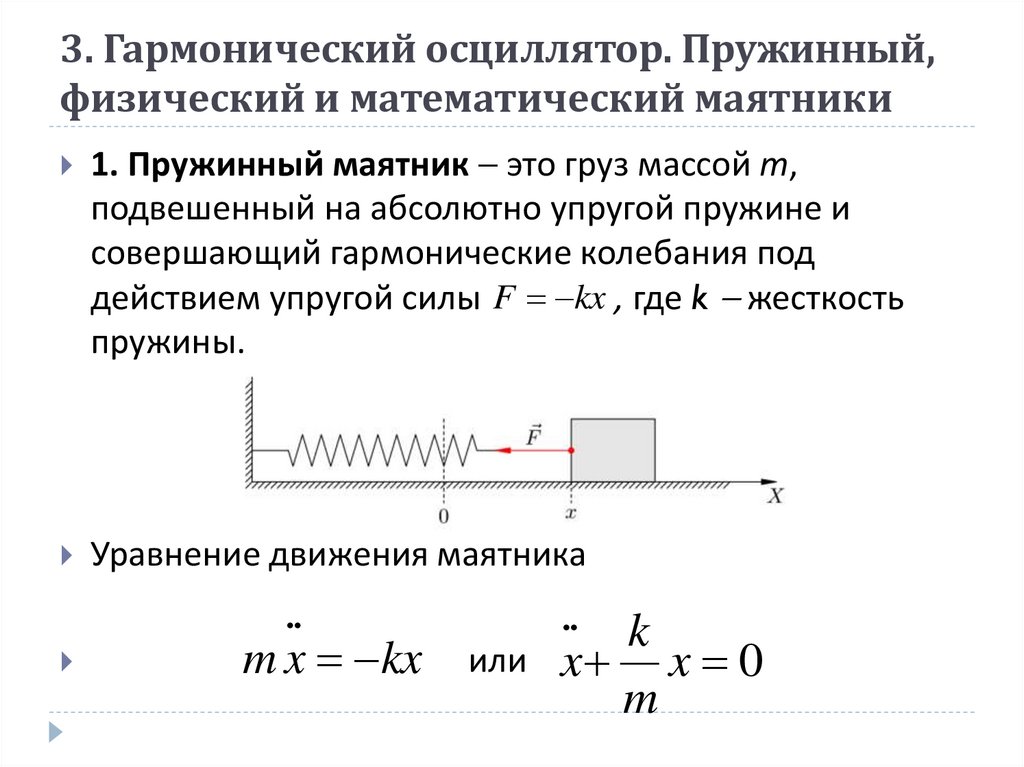
1. Пружинный маятник это груз массой т,
подвешенный на абсолютно упругой пружине и
совершающий гармонические колебания под
действием упругой силы F kx , где k жесткость
пружины.
Уравнение движения маятника
..
m x kx
..
или
k
x x 0
m

17. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

Циклическая частота:
k
0
m
Период:
m
T 2
k
Потенциальная энергия пружинного маятника равна:
kx 2
П
2

18. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

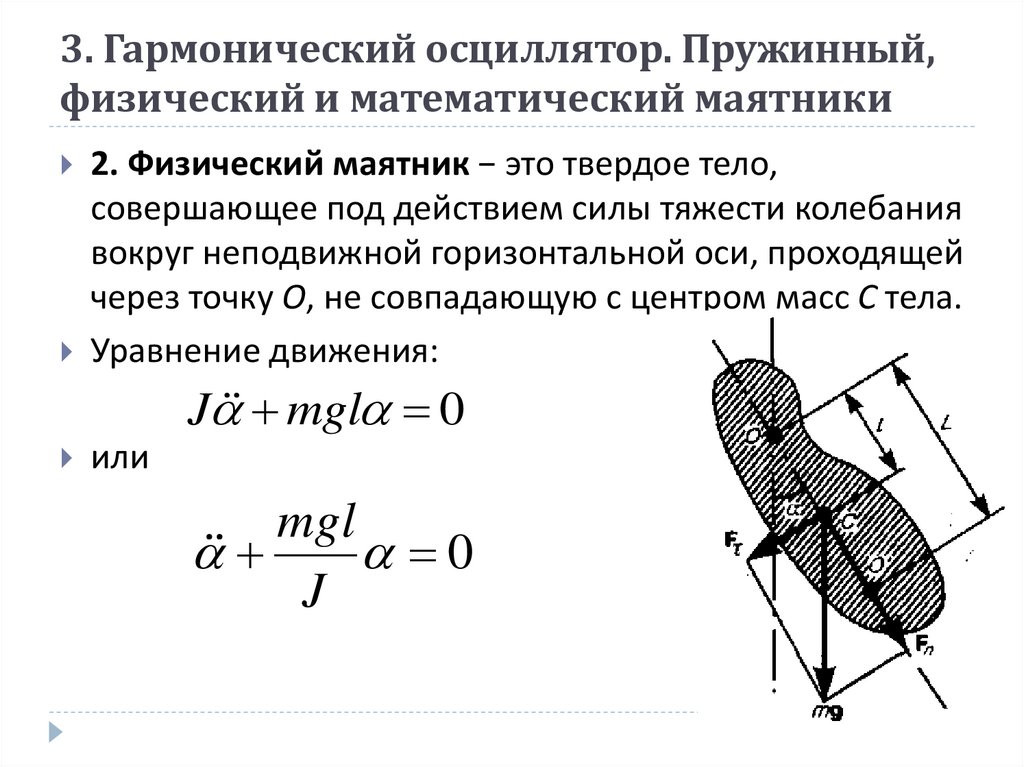
2. Физический маятник − это твердое тело,
совершающее под действием силы тяжести колебания
вокруг неподвижной горизонтальной оси, проходящей
через точку О, не совпадающую с центром масс С тела.
Уравнение движения:
J mgl 0
или
mgl
0
J

19. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

Принимая
mgl
0
J
получим уравнение
0
2
0
Решение уравнения:
0 cos 0t
Период колебаний:
2
L
T
2
0
g

20. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

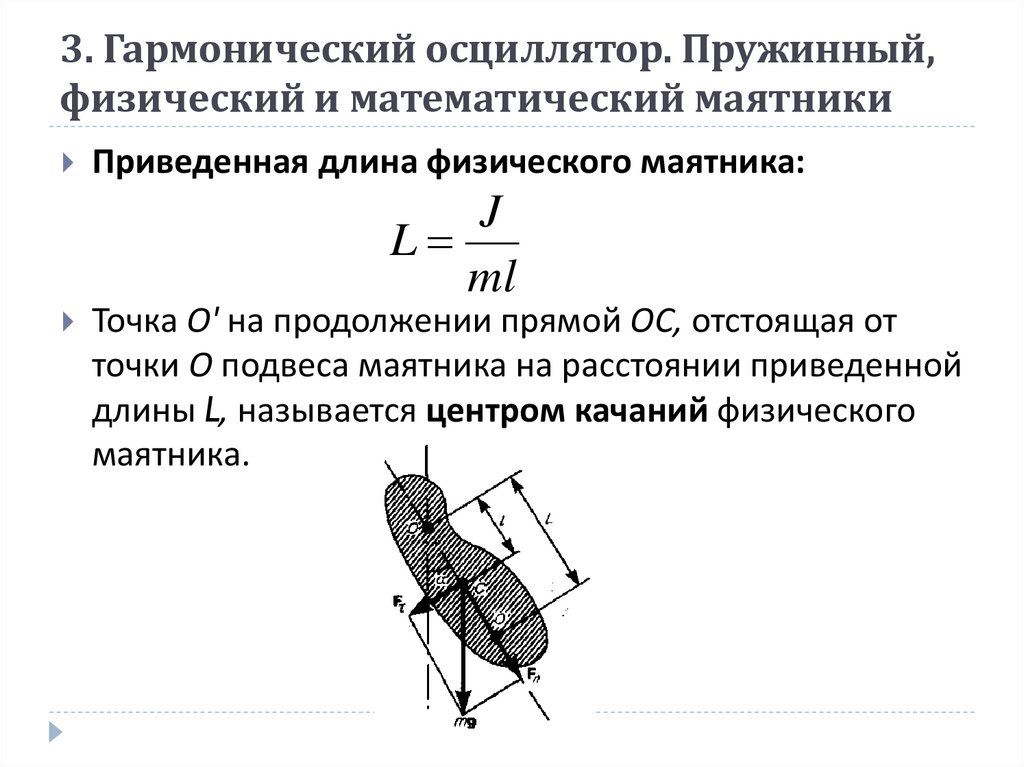
Приведенная длина физического маятника:
J
L
ml
Точка О' на продолжении прямой ОС, отстоящая от
точки О подвеса маятника на расстоянии приведенной
длины L, называется центром качаний физического
маятника.

21. 3. Гармонический осциллятор. Пружинный, физический и математический маятники

3. Математический маятник − это идеализированная
система, состоящая из материальной точки массой т,
подвешенной на нерастяжимой невесомой нити, и
колеблющаяся под действием силы тяжести.
Момент инерции материальной точки:
J ml
2
Подставим в формулу:
J
T 2
m lg
Период колебаний:
l
T 2
g

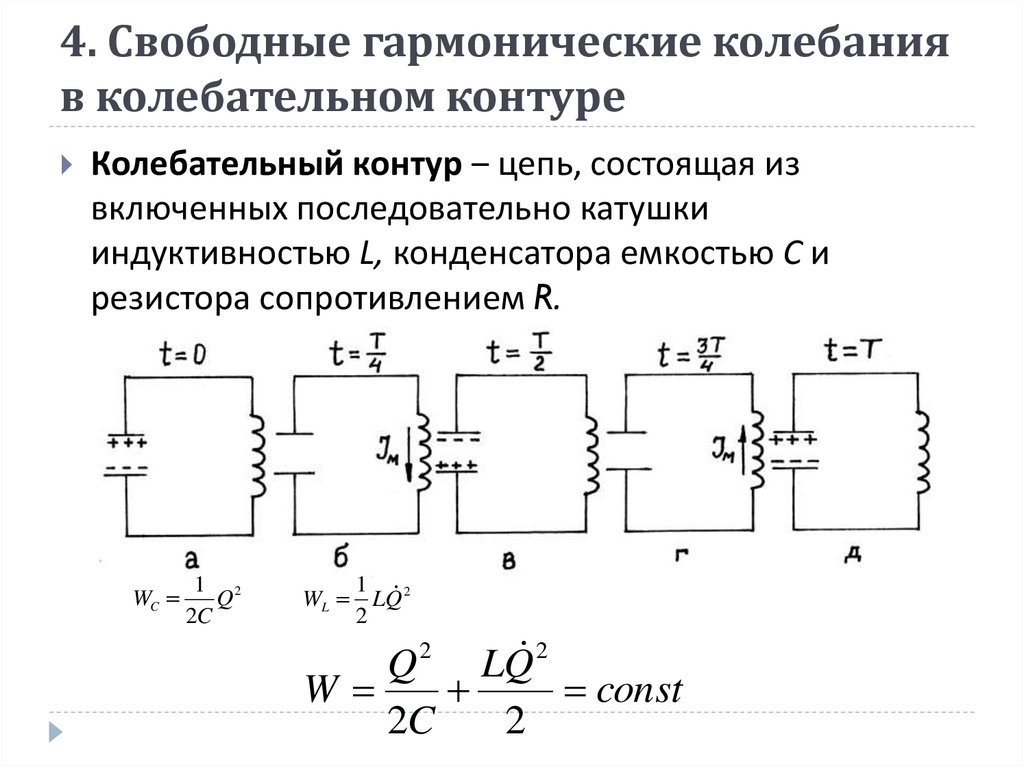
22. 4. Свободные гармонические колебания в колебательном контуре

Колебательный контур ‒ цепь, состоящая из
включенных последовательно катушки
индуктивностью L, конденсатора емкостью С и
резистора сопротивлением R.
WC
1 2
Q
2C
WL
1 2
LQ
2
Q 2 LQ 2
W
const
2C
2

23. 4. Свободные гармонические колебания в колебательном контуре

Дифференциальное уравнение свободных
гармонических колебаний заряда в контуре:
1
Q
Q 0
LC
Заряд Q совершает гармонические колебания по
закону:
Q Qm cos 0t
Собственная частота контура:
0
1
LC

24. 4. Свободные гармонические колебания в колебательном контуре

Период (формула Томсона):
T 2 LC
Сила тока в колебательном контуре:
I Q 0Qm sin 0t I m cos 0t
2
Напряжение на конденсаторе:
Q Qm
UC
cos 0t U m cos 0t
C C