Similar presentations:
Колебания. Гармонические колебания. Векторная диаграмма
1. Лекция 5. «КОЛЕБАНИЯ»
• Гармонические колебания• Векторная диаграмма
• Сложение гармонических колебаний одного
направления равных и близких частот
• Сложение взаимно перпендикулярных
гармонических колебаний равных и кратных
частот
• Свободные незатухающие колебания
• Энергия и импульс гармонического осциллятора
• Фазовая траектория
• Физический маятник
• Квазиупругая сила
А.С. Чуев, 2020 г.
1
2.
Любая физическая теория, в конечном счете,сводится к маятнику.
Высказывание ученых
Новая идея появляется в результате сравнения
двух вещей, которые еще не сравнивали
Гельвеций
А.С. Чуев, 2020 г.
2
3.
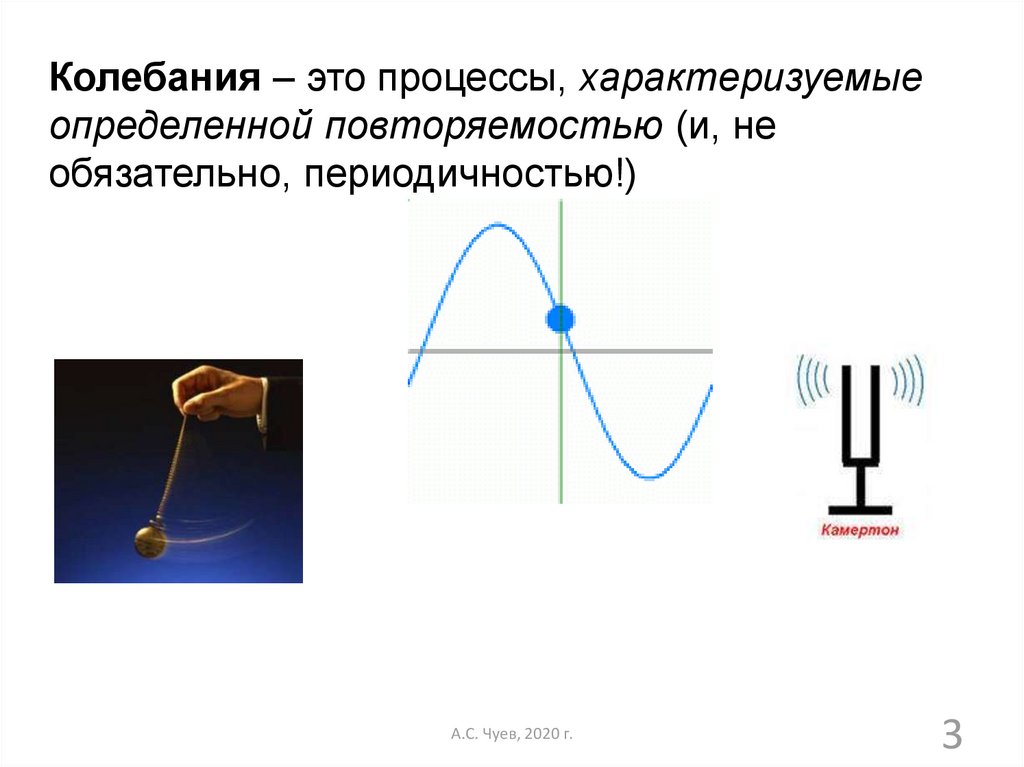
Колебания – это процессы, характеризуемыеопределенной повторяемостью (и, не
обязательно, периодичностью!)
А.С. Чуев, 2020 г.
3
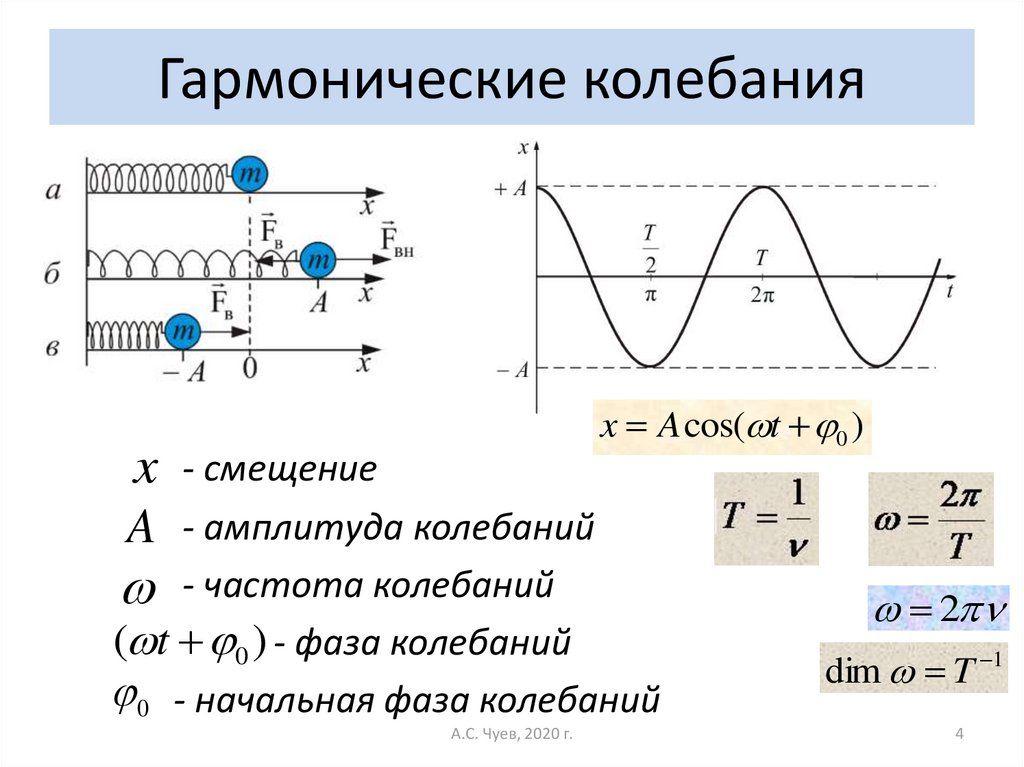
4. Гармонические колебания
x A cos( t 0 )x
A
- смещение
- амплитуда колебаний
- частота колебаний
( t 0 ) - фаза колебаний
0 - начальная фаза колебаний
А.С. Чуев, 2020 г.
2
dim T 1
4
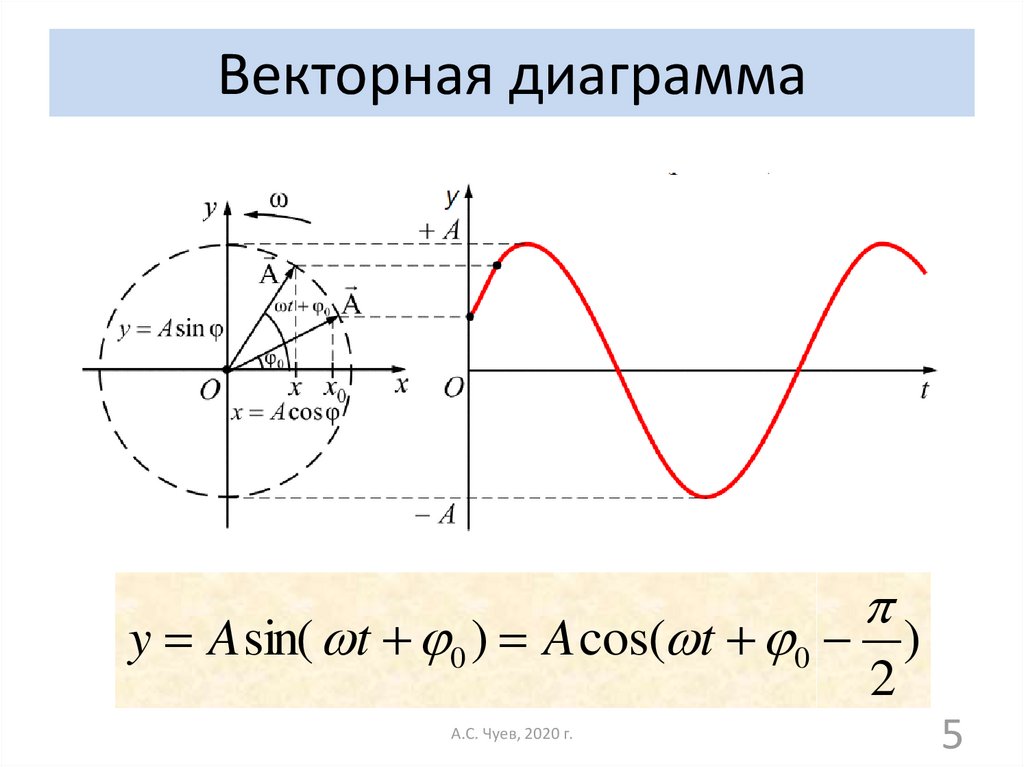
5. Векторная диаграмма
y A sin( t 0 ) A cos( t 0 )2
А.С. Чуев, 2020 г.
5
6. Анимация
А.С. Чуев, 2020 г.6
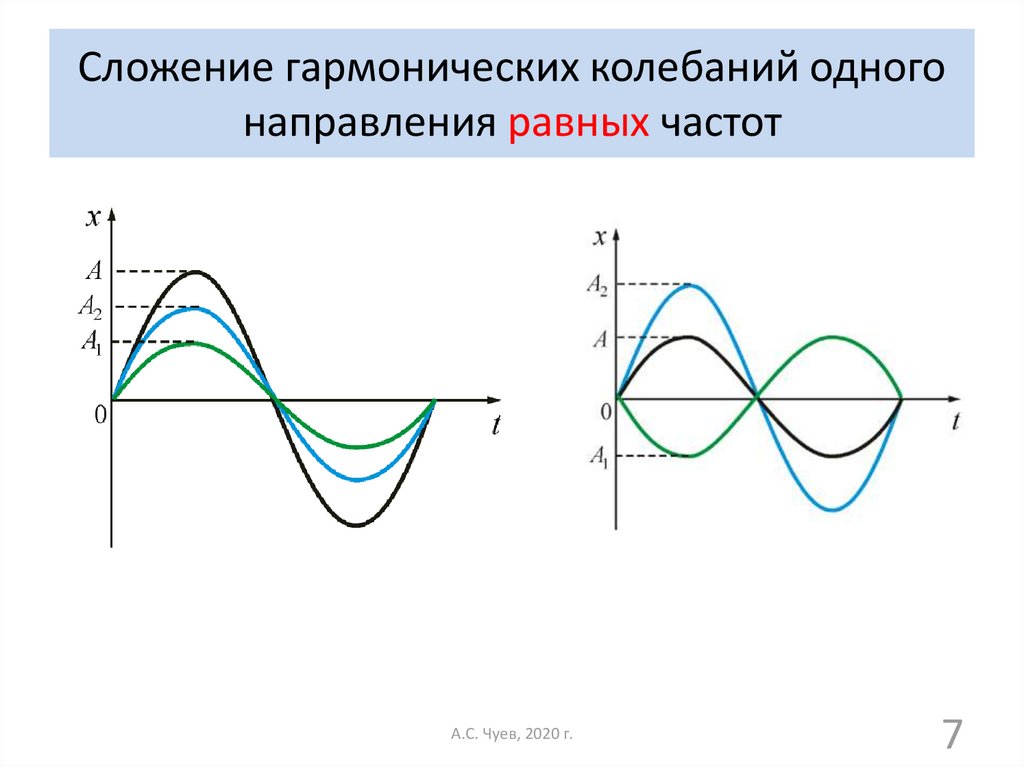
7. Сложение гармонических колебаний одного направления равных частот
А.С. Чуев, 2020 г.7
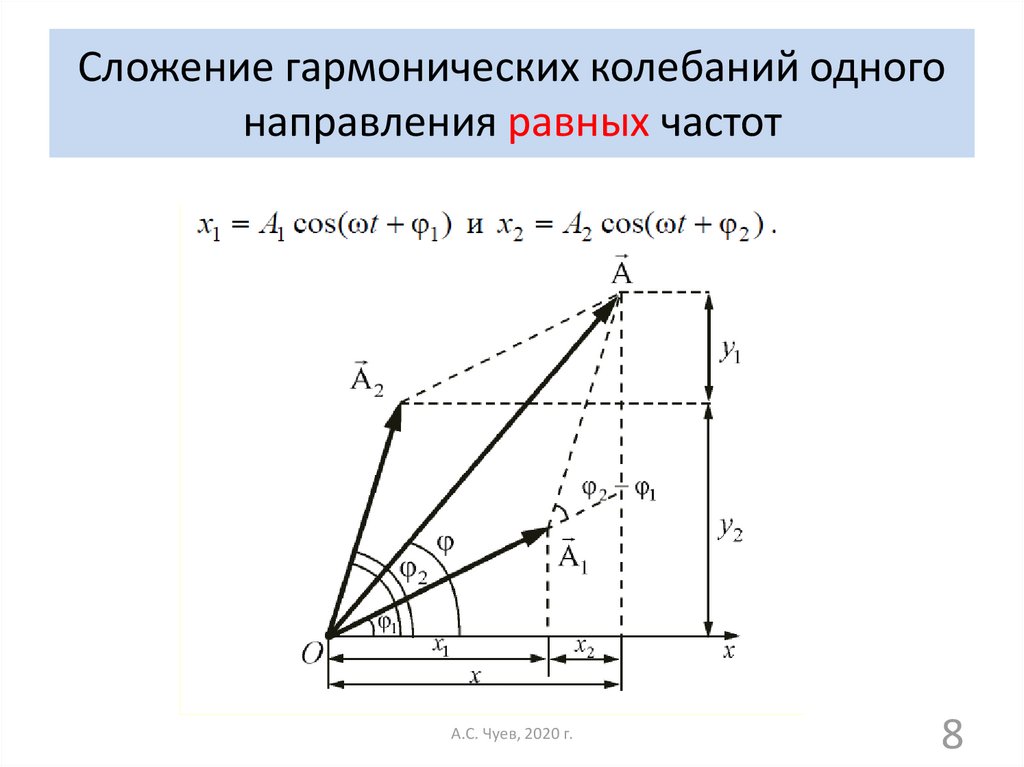
8. Сложение гармонических колебаний одного направления равных частот
А.С. Чуев, 2020 г.8
9. Сложение гармонических колебаний одного направления равных частот
А.С. Чуев, 2020 г.9
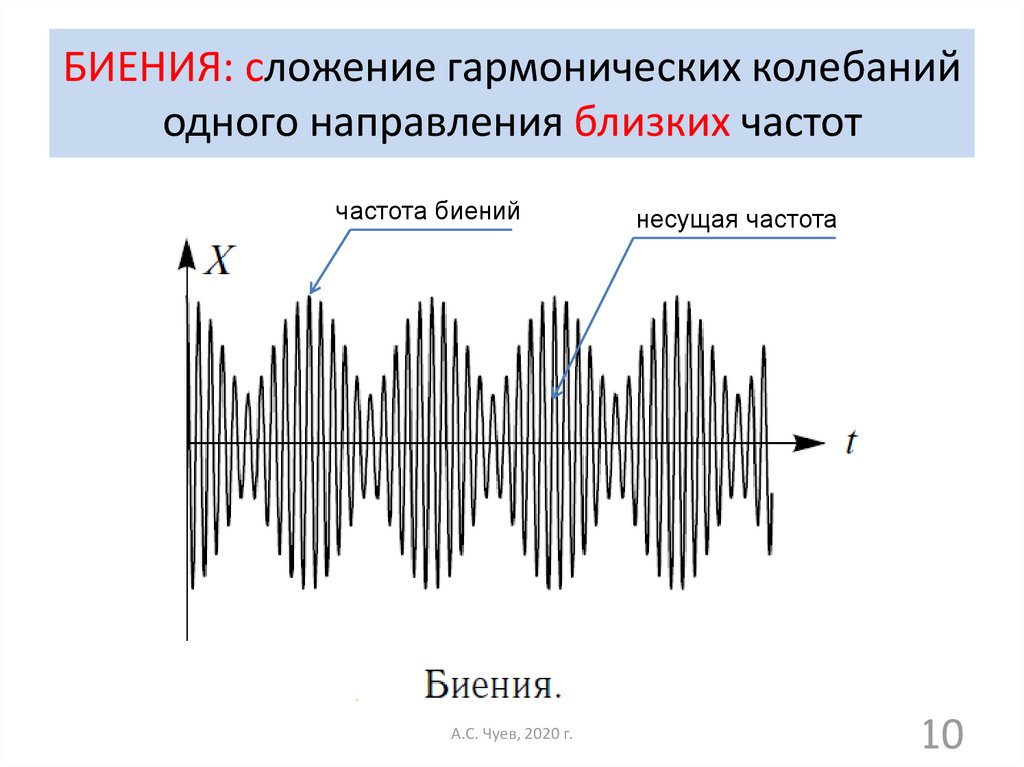
10. БИЕНИЯ: сложение гармонических колебаний одного направления близких частот
частота биенийА.С. Чуев, 2020 г.
несущая частота
10
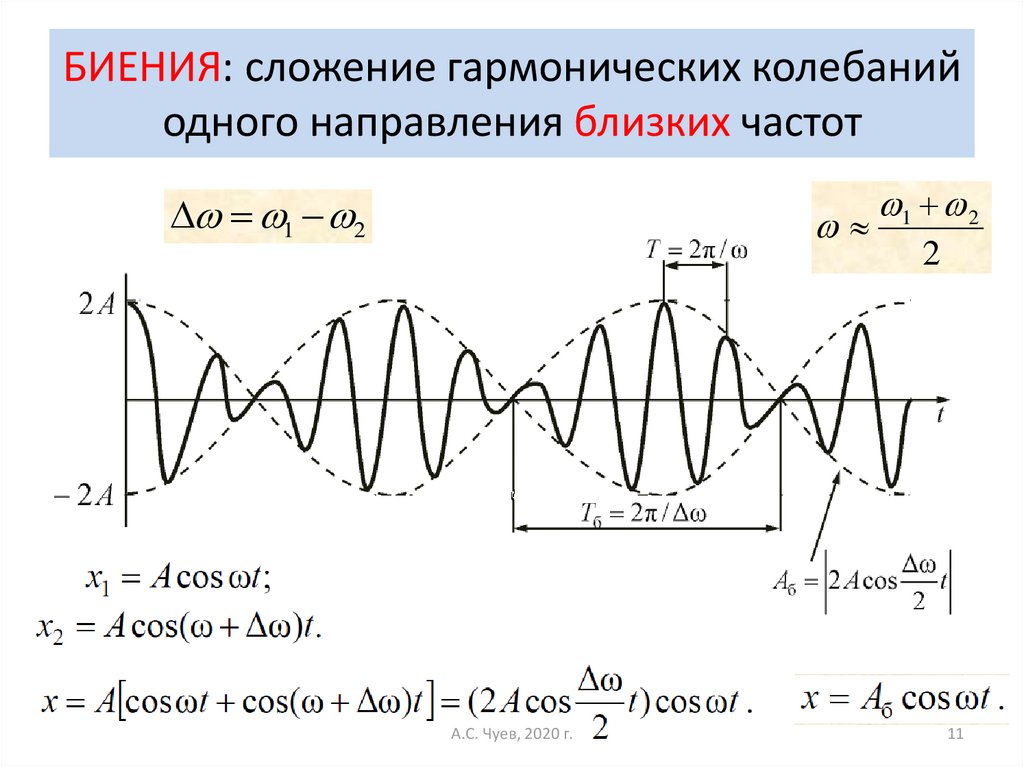
11. БИЕНИЯ: сложение гармонических колебаний одного направления близких частот
1 2А.С. Чуев, 2020 г.
1 2
2
11
12.
Анимация биений двухсинусоидальных сигналов
напряжения равной амплитуды
близких частот. Колебания и их
сумма изображены в виде
вращающихся векторов
А.С. Чуев, 2020 г.
(комплексных амплитуд).
12
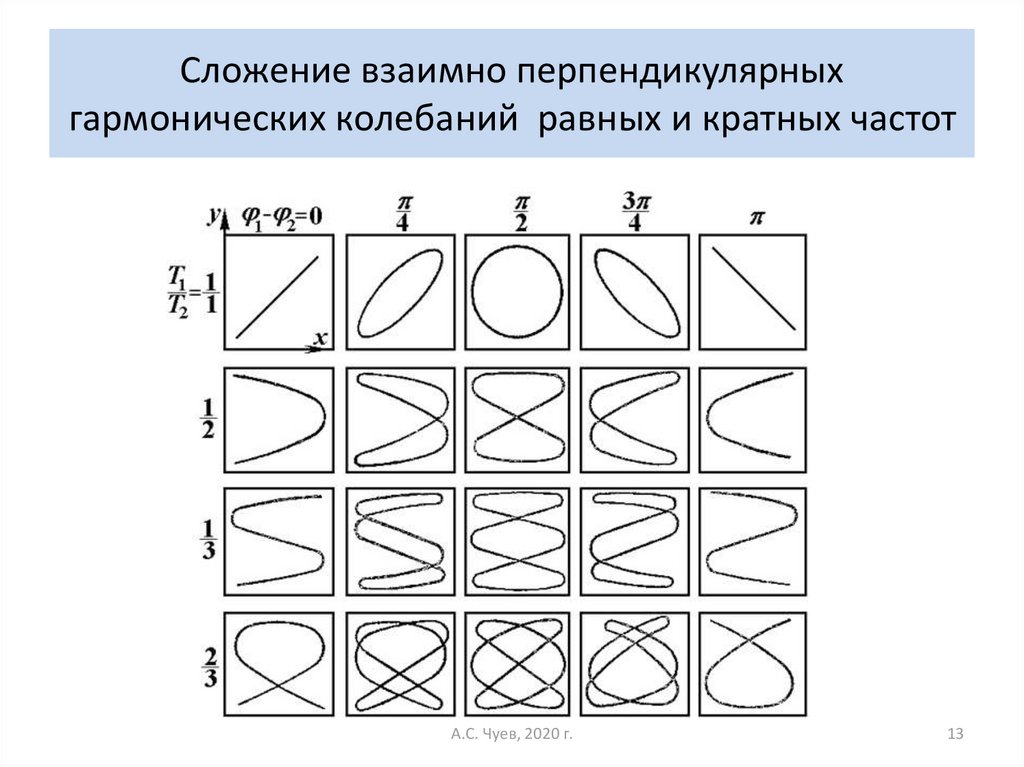
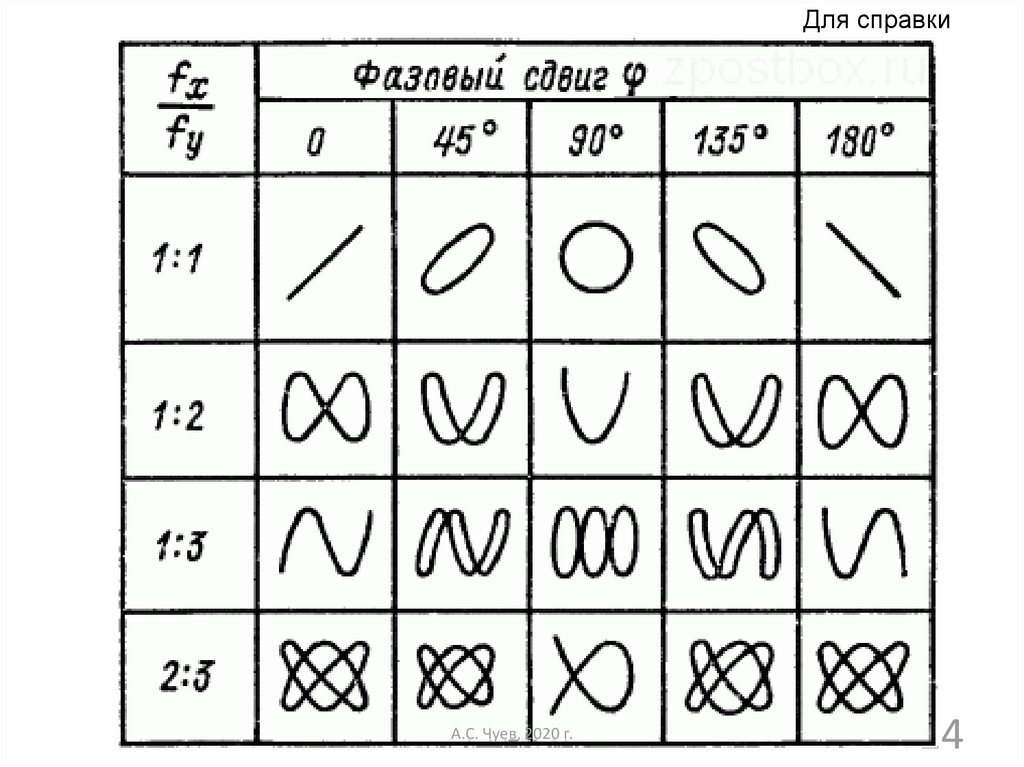
13. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот
А.С. Чуев, 2020 г.13
14.
Для справкиА.С. Чуев, 2020 г.
14
15.
А.С. Чуев, 2020 г.15
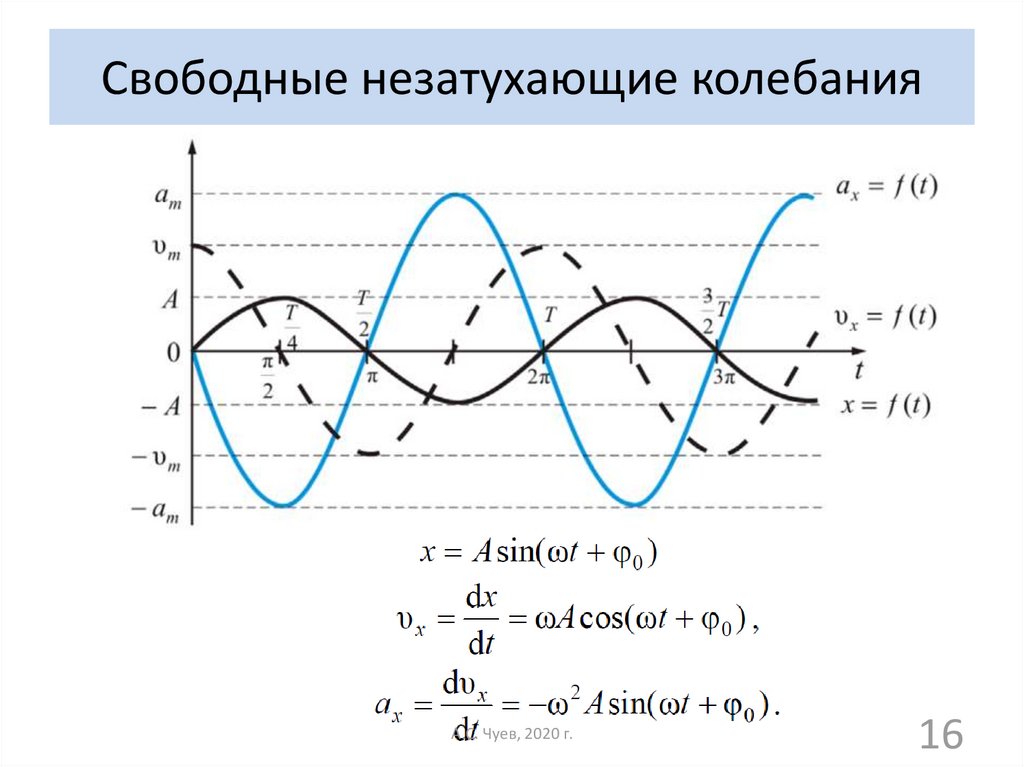
16. Свободные незатухающие колебания
А.С. Чуев, 2020 г.16
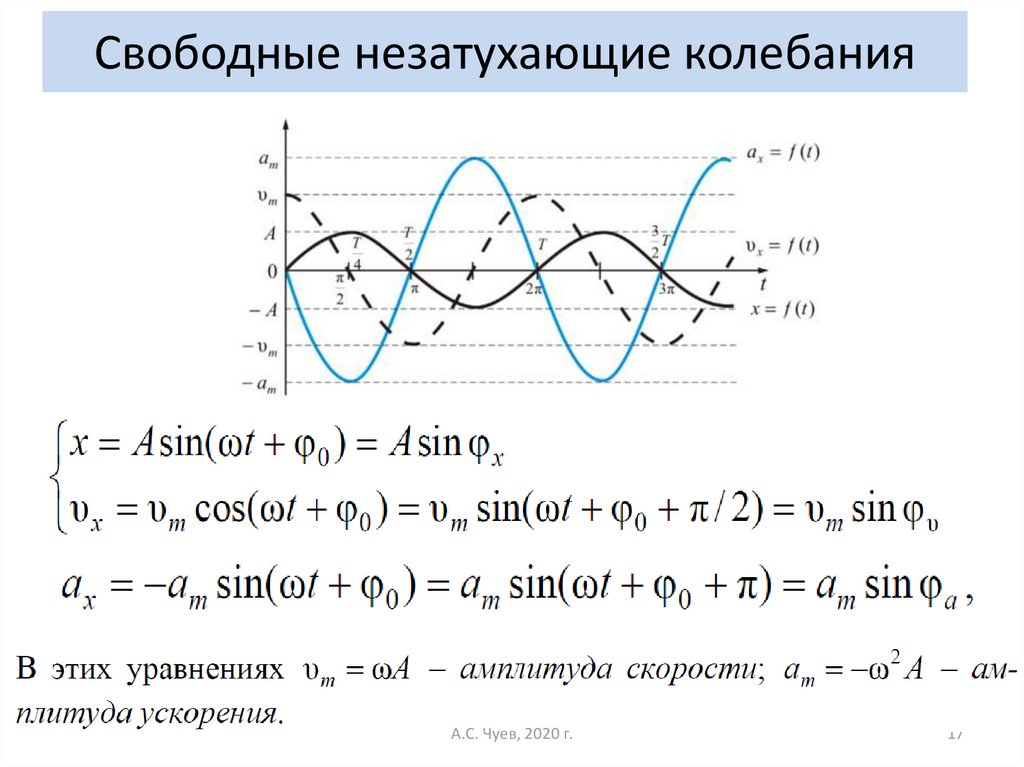
17. Свободные незатухающие колебания
А.С. Чуев, 2020 г.17
18. Гармонический осциллятор
m x FF kx
k
x x 0
m
x x 0
Решение дифф. уравнения:
2
m x kx 0
k
m
x A cos( t 0 )
А.С. Чуев, 2020 г.
18
19. Энергия и импульс гармонического осциллятора
Потенциальная энергияПолная энергия:
Т.к.:
А.С. Чуев, 2020 г.
19
20.
Полная энергияпропорциональна квадрату
амплитуды колебаний
Кинетическая и
потенциальная энергии
изменяются с удвоенной
частотой
U
А.С. Чуев, 2020 г.
20
21. Энергия и импульс гармонического осциллятора
P mxmx 2 m 2 x 2 P 2
К
2
2m
2m
P 2mK
А.С. Чуев, 2020 г.
21
22. Фазовая траектория
Пространство с осями «координата – импульс»называется фазовым пространством
Траектория гармонического осциллятора в фазовом пространстве
А.С. Чуев, 2020 г.
22
23.
А.С. Чуев, 2020 г.23
24.
Фазовый портрет линейного одномерного осциллятораФазовая плоскость –пространство состояний осциллятора
Фазовая траектория
( x, x )
x F ( x;W )
x2
x2
2 2 1
2
A
A 0
Колебательное движение с
заданной амплитудой (энергией)
изображается фазовой
траекторией в виде эллипса с
полуосями
a A; b A 0
А.С. Чуев, 2020 г.
24
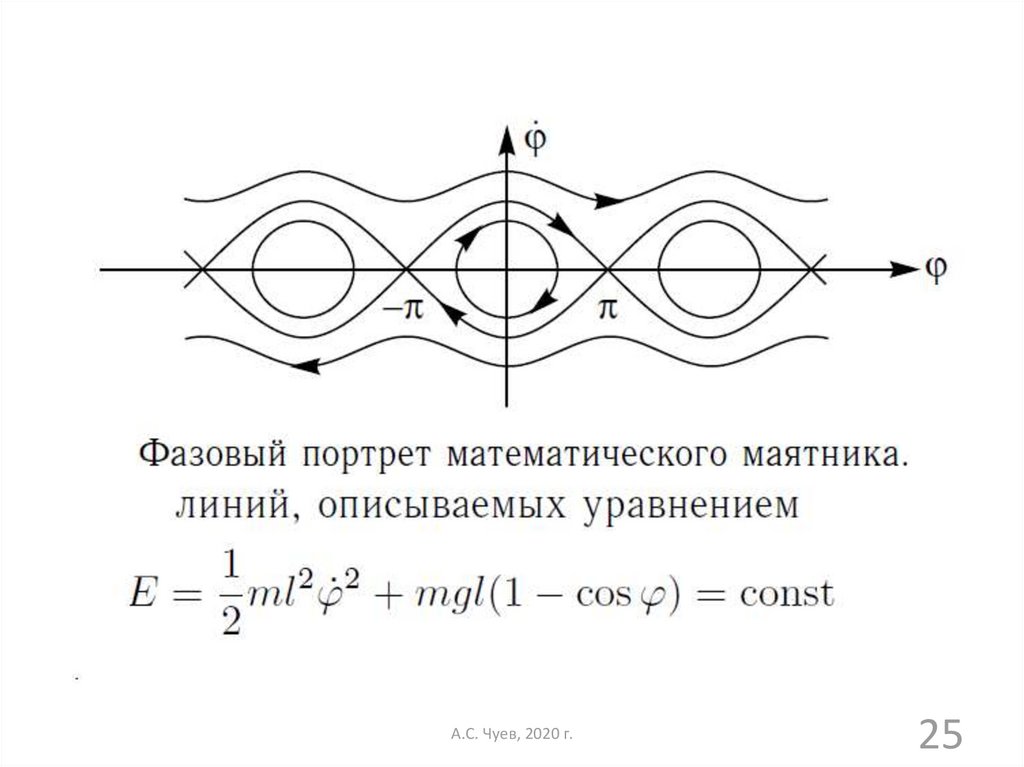
25.
А.С. Чуев, 2020 г.25
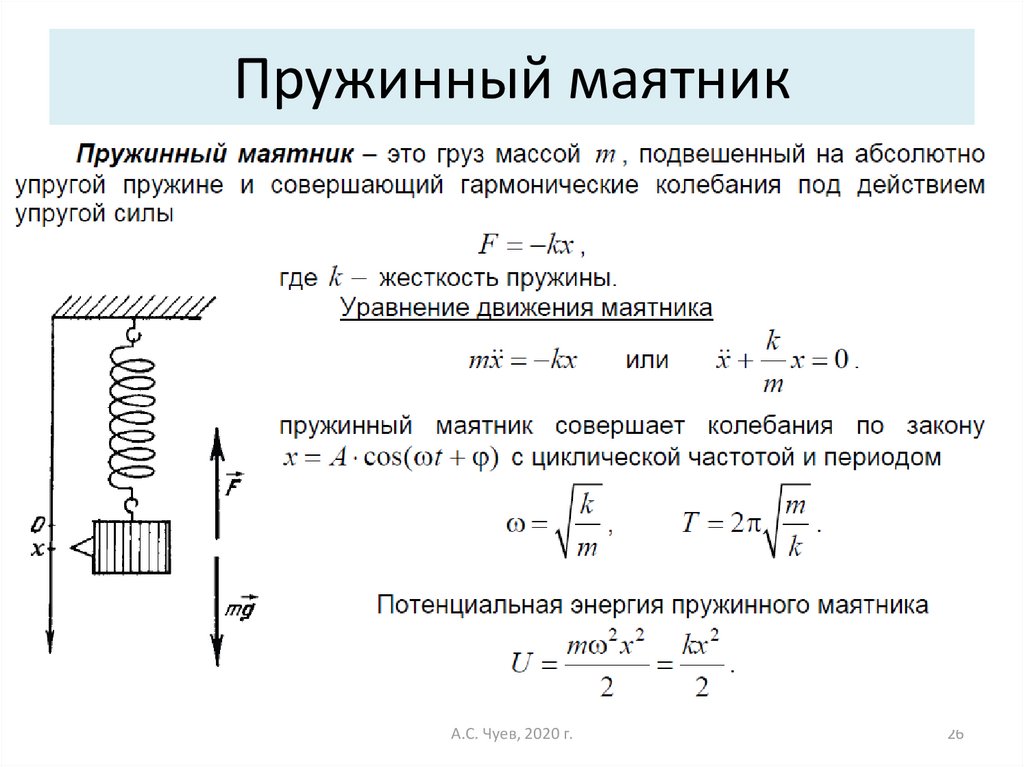
26. Пружинный маятник
А.С. Чуев, 2020 г.26
27. Математический маятник
ММ – математическая точка (телопренебрежимо малых размеров),
подвешенная в поле тяжести на
невесомой и нерастяжимой нити
mgl sin
I
Так как
I ml
g
sin 0
l
и
2
sin
Решение дифф. уравнения:
x A cos( t 0 )
А.С. Чуев, 2020 г.
27
28.
Вывод дифференциального уравнения черезэнергетические соотношения
факультативно
А.С. Чуев, 2020 г.
28
29.
факультативноА.С. Чуев, 2020 г.
29
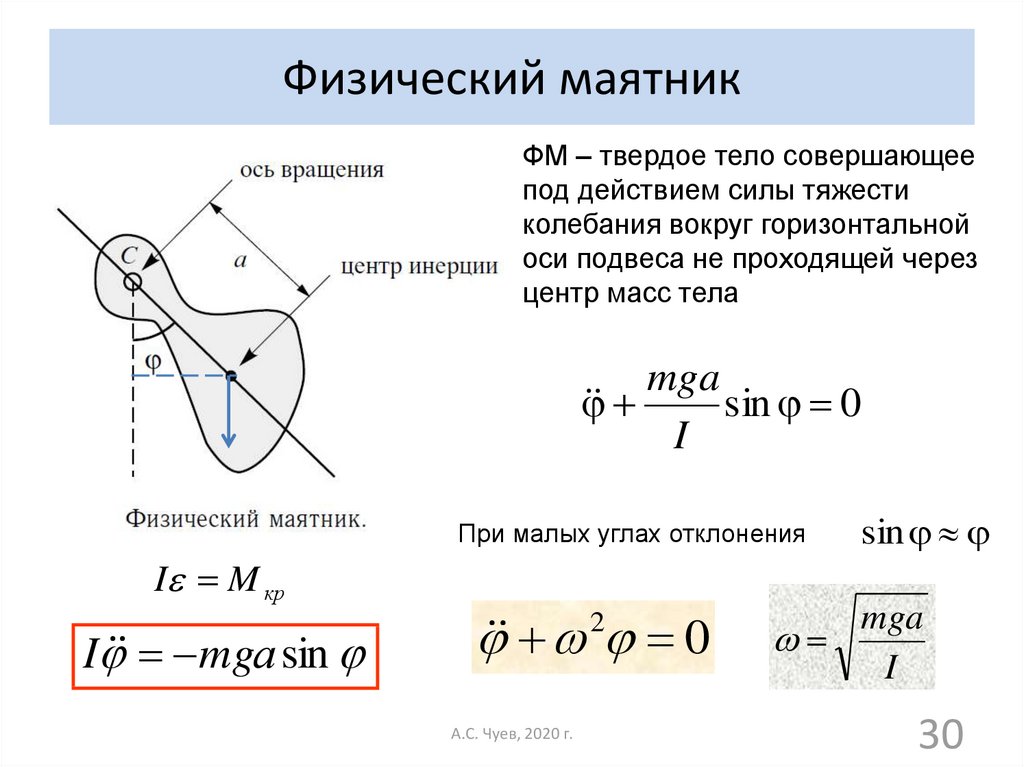
30. Физический маятник
ФМ – твердое тело совершающеепод действием силы тяжести
колебания вокруг горизонтальной
оси подвеса не проходящей через
центр масс тела
mga
sin 0
I
При малых углах отклонения
I M кр
I mgа sin
0
2
А.С. Чуев, 2020 г.
sin
mga
I
30
31.
Вывод дифференциального уравнения черезэнергетические соотношения
факультативно
А.С. Чуев, 2020 г.
31
32.
Центр качаний физического маятника (ФМ)Точка тела, лежащая на линии соединения точки подвеса и центра масс и
удаленная от точки подвеса на расстояние, равное приведенной длине l
пр
называется центром качаний физического маятника (точка O на
рисунке).
Если в центре качаний сосредоточить всю массу системы, то физический
маятник превращается в математический маятник с той же собственной
частотой колебаний 0
Приведенная длина физического
маятника равна длине математического
маятника, период колебаний которого
совпадает с периодом колебаний ФМ.
Центр качаний удален от точки подвеса
дальше, чем центр масс:
А.С. Чуев, 2020 г.
lпр lC
32
33.
Теорема ГюйгенсаЕсли точку подвеса и центр качаний поменять местами («оборотный
маятник»), частота колебаний маятника не изменится.
А.С. Чуев, 2020 г.
33
34.
ПовторТеорема Гюйгенса
А.С. Чуев, 2020 г.
34
35.
Запомнить и уметь выводить!А.С. Чуев, 2020 г.
35
36. Квазиупругая сила
Квазиупругими силами называют силы,физическая природа которых отлична от природы
упругих сил, но определяющая их зависимость
имеет вид:
FX kx
где k – постоянный коэффициент, а х –
смещение относительно положения равновесия.
А.С. Чуев, 2020 г.
36
37.
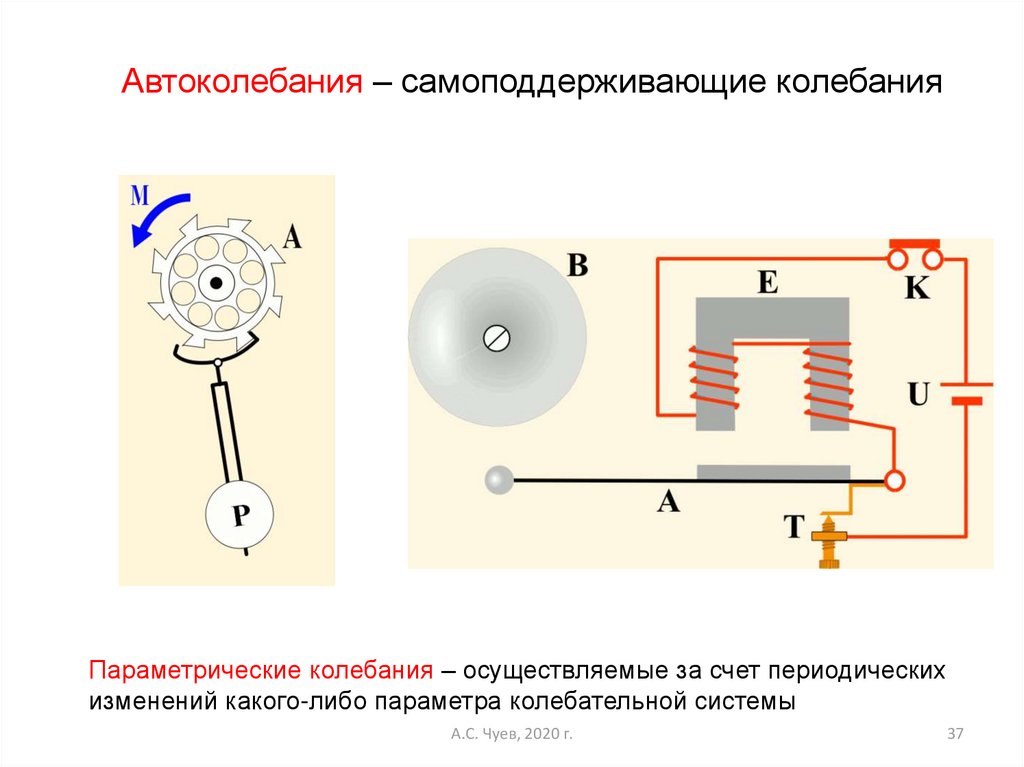
Автоколебания – самоподдерживающие колебанияПараметрические колебания – осуществляемые за счет периодических
изменений какого-либо параметра колебательной системы
А.С. Чуев, 2020 г.
37
38.
А.С. Чуев, 2020 г.38
39.
Конец лекции 5А.С. Чуев, 2020 г.
39























 physics
physics








