Similar presentations:
Гармонические колебания
1.
ГАРМОНИЧЕСКИЕКОЛЕБАНИЯ
2.
3.
• Вынужденные колебания –подвоздействием внешнего периодически
меняющегося воздействия на систему.
• Свободные (или собственные) колебания
происходят под действием внутренних сил.
• Автоколебания – это колебания, при
которых система имеет некоторый
собственный запас потенциальной энергии,
который расходуется на совершение
колебаний (например, механические часы).
4.
• Колебания- движения или процессы,которые характеризуются
определенной повторяемостью во
времени
• Природа колебаний может быть
различна, однако все они описываются
одинаковыми уравнениями
5.
• Колебания называютсягармоническими, если они происходят
по закону синуса(косинуса)
6.
s A cos( 0t 0 )Максимальное значение
A -колеблющейся
величины –
0
амплитуда колебаний
- Круговая (циклическая) частота
0t 0
0
- Фаза колебаний
- Начальная
фаза колебаний
7.
• Период колебаний – это время , закоторое фаза колебаний изменяется на 2π
0T 2
T
2
0
8.
Частота колебаний1
n
T
-число полных колебаний,
совершаемых в единицу времени
0 2 n
9.
s A cos( 0t 0 )ds d
A cos( 0t 0 )
dt dt
A 0 sin( 0t 0 )
10.
2d s d
A
sin(
t
)
0
0
0
2
dt
dt
A 0 cos( 0t 0 )
2
0 s
2
2
d s
2
s
0
0
2
dt
11.
sT
А
t
-А
T
12.
2d s
2
s
0
0
2
dt
Дифференциальное
уравнение
гармонических
колебаний
s 0 s 0
2
s A cos( 0t 0 )
Решение
уравнения
13.
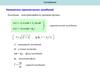
• Гармонические колебания можноизображать с помощью векторных
диаграмм
• Откладывается вектор, длина которого
равна АМПЛИТУДЕ колебаний
• Угол, под которым он расположен к оси
х – начальная фаза колебаний
14.
0А
0
х
Проекция вектора на ось х
меняется по гармоническому закону
x A cos( 0t 0 )
15.
Механические гармоническиеколебания
16.
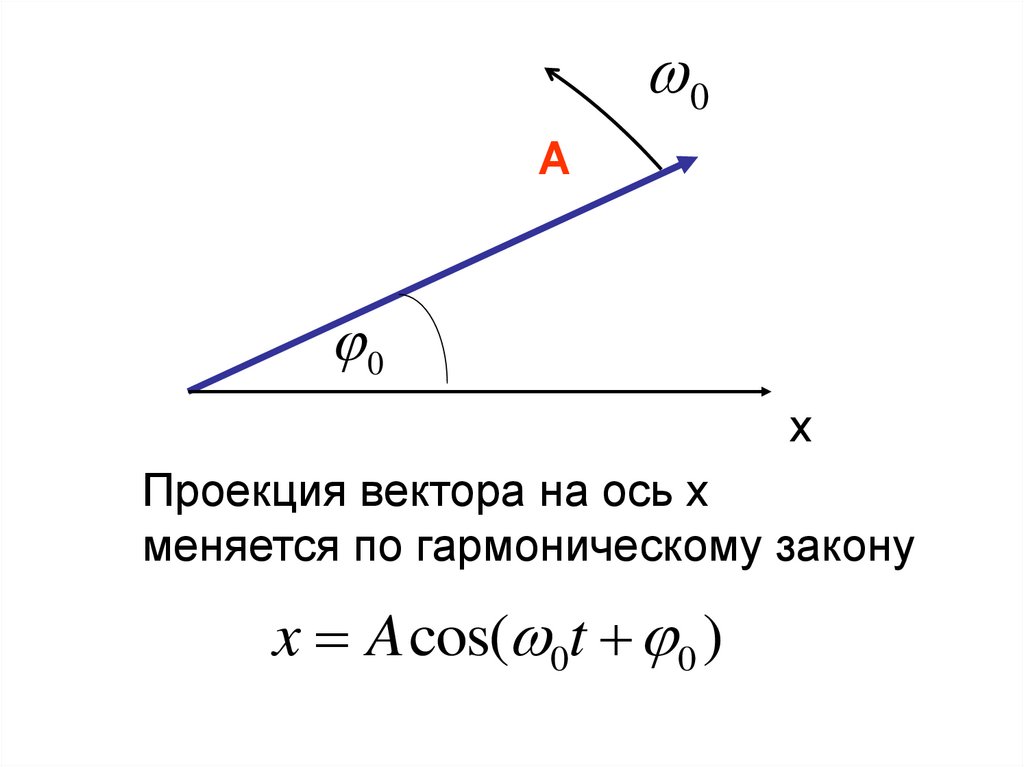
• Пусть мат. точка совершаетгармонические колебания вокруг
положения равновесия вдоль оси Х
x(t ) A cos( 0t 0 )
dx (t )
V (t )
dt
A 0 sin( 0t 0 )
17.
xA
π
2π
3π
4π
5π
ω0 t
-A
V
Aw
ω0t
-Aw
18.
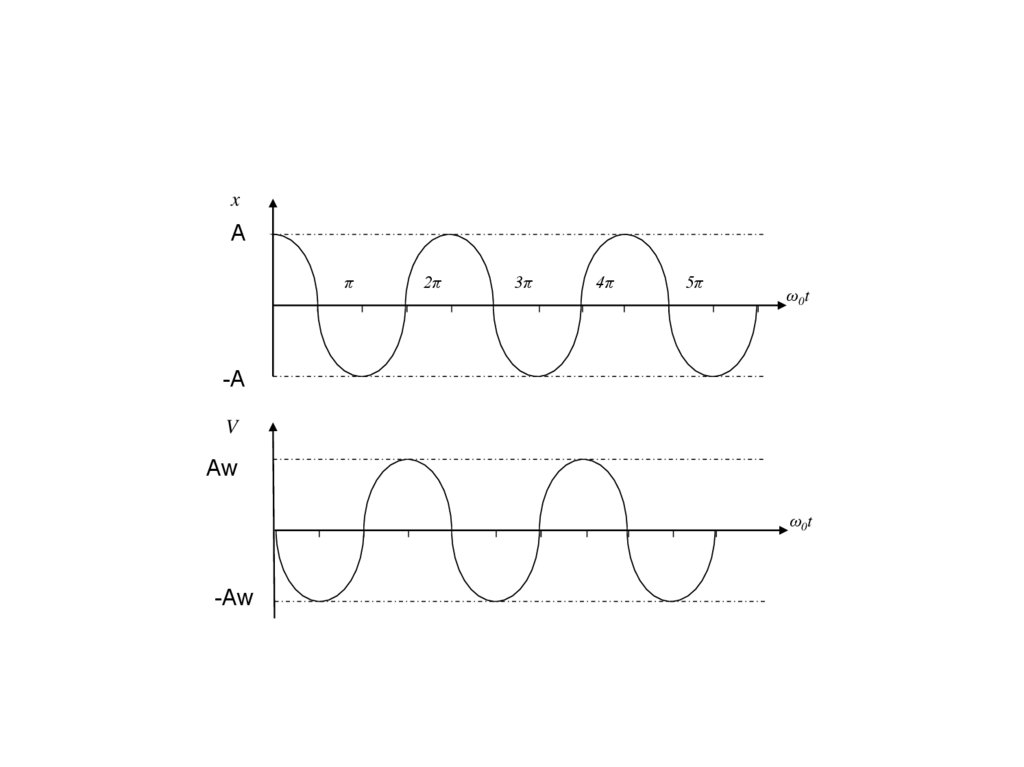
2dV (t )
d V (t )
a(t )
2
dt
dt
A 0 cos( 0t 0 )
2
0 x
2
F m 0 x
2
19.
Кинетическая энергияmV
T
2
2
mA 0 sin ( 0t 0 )
2
2
2
2
20.
Потенциальная энергияx
x
0
0
П Fdx madx
m x
m xdx
2
0
x
2
0
2
0
2
m A cos ( 0t 0 )
2
2
0
2
2
21.
Полная энергияE T П
mA 0 sin ( 0t 0 )
2
2 2
2
mA 0 cos ( 0t 0 )
2
2
2
mA 0
const
2
2
2
2
22.
Гармонический осциллятор• Гармоническим осциллятором наз.
система, совершающая колебания,
описываемые уравнением
2
d s
2
s
0
0
2
dt
s 0 s 0
2
23.
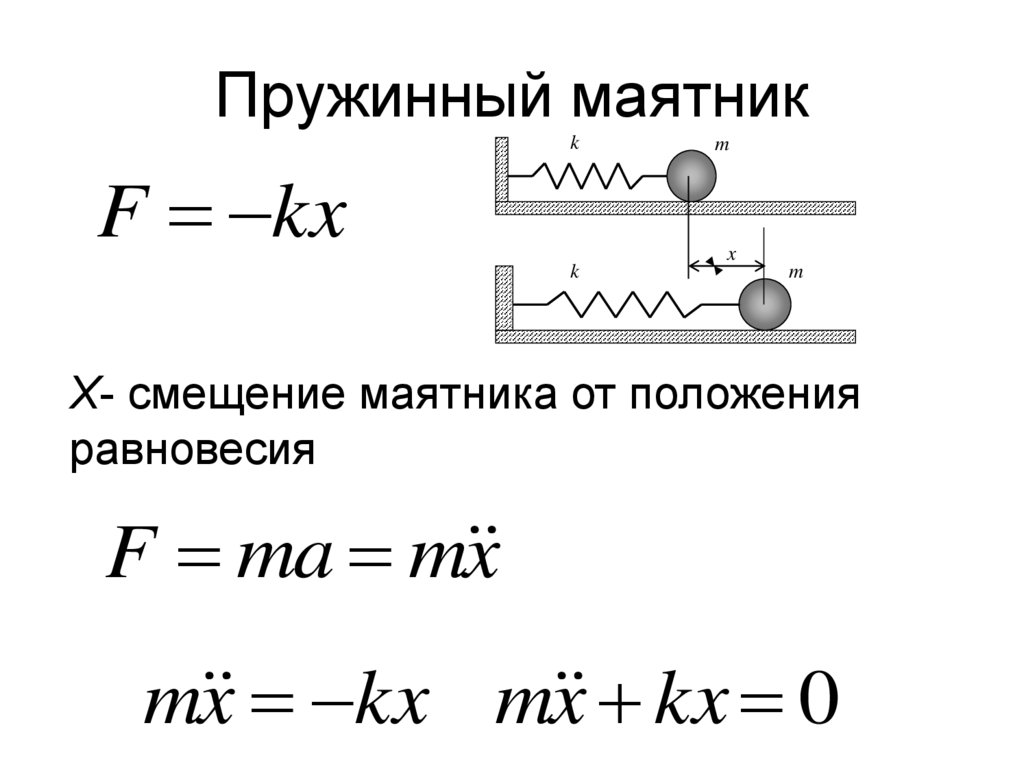
Пружинный маятникk
F kx
k
m
x
m
X- смещение маятника от положения
равновесия
F ma m x
m x kx m x kx 0
24.
m x kx 0k
x x 0
m
x 0 x 0
k
0
m
2
2
25.
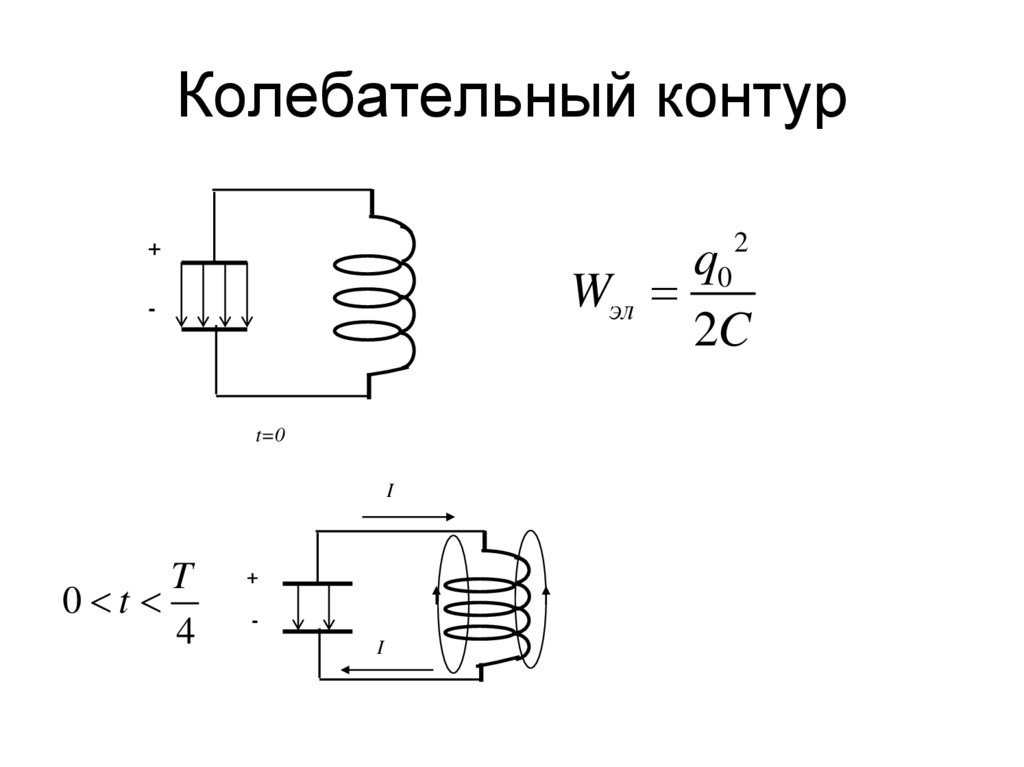
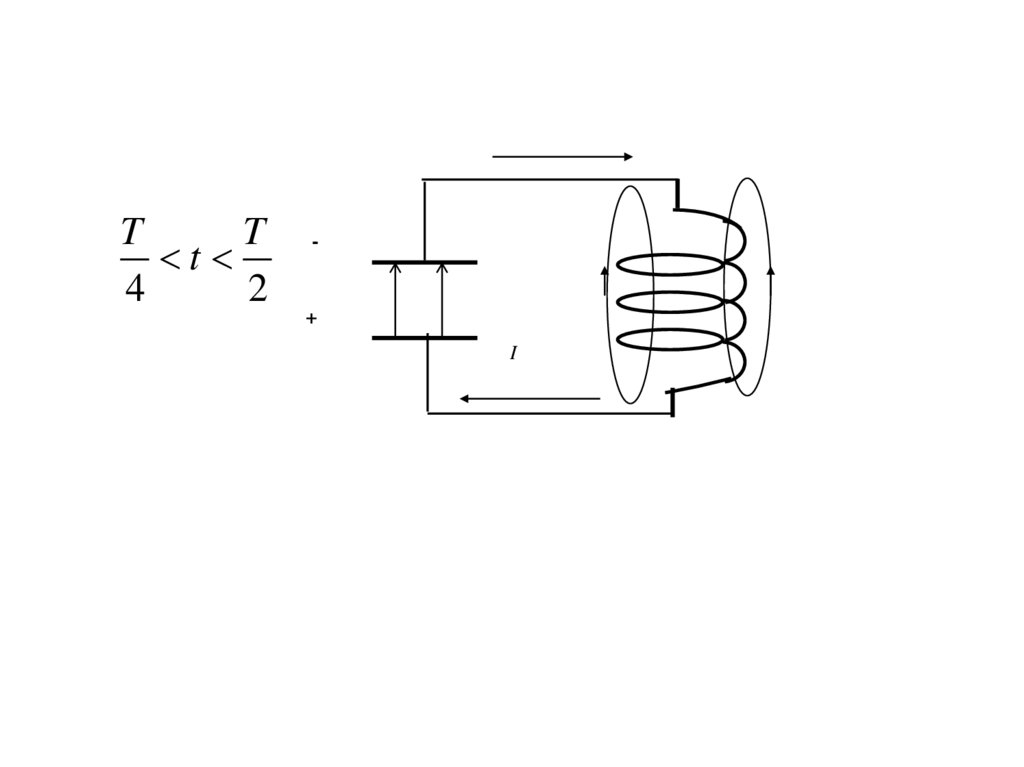
Колебательный контур2
+
q0
Wэл
2C
-
t=0
I
T
0 t
4
+
I
26.
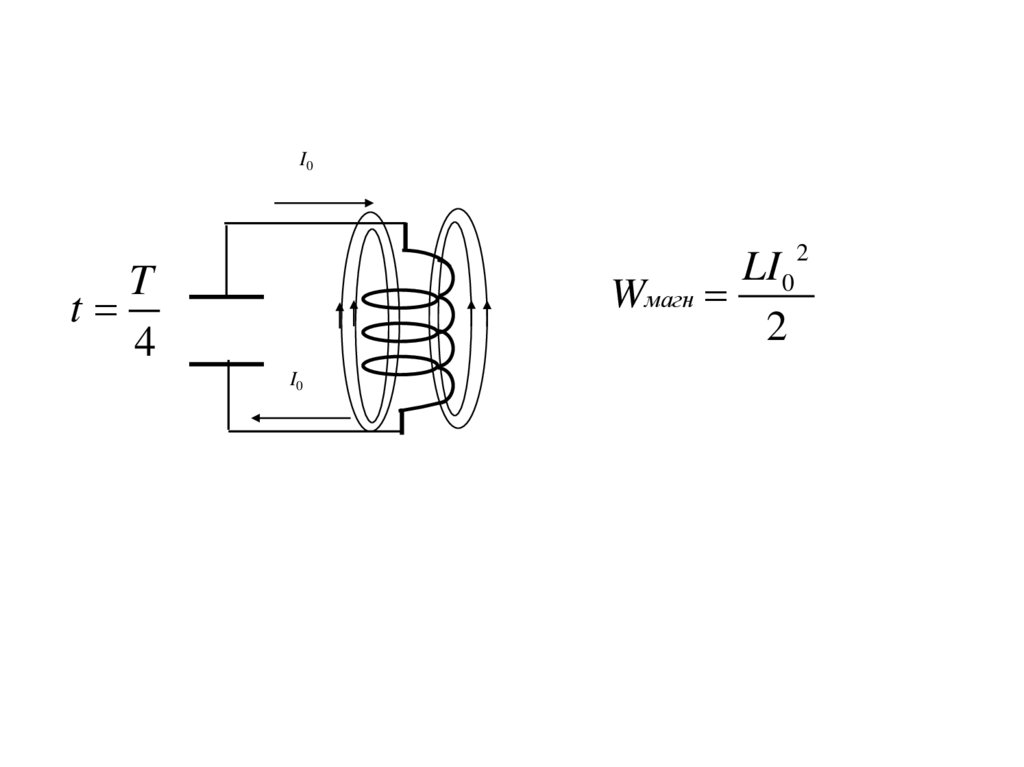
I0LI 0
Wмагн
2
T
t
4
I0
2
27.
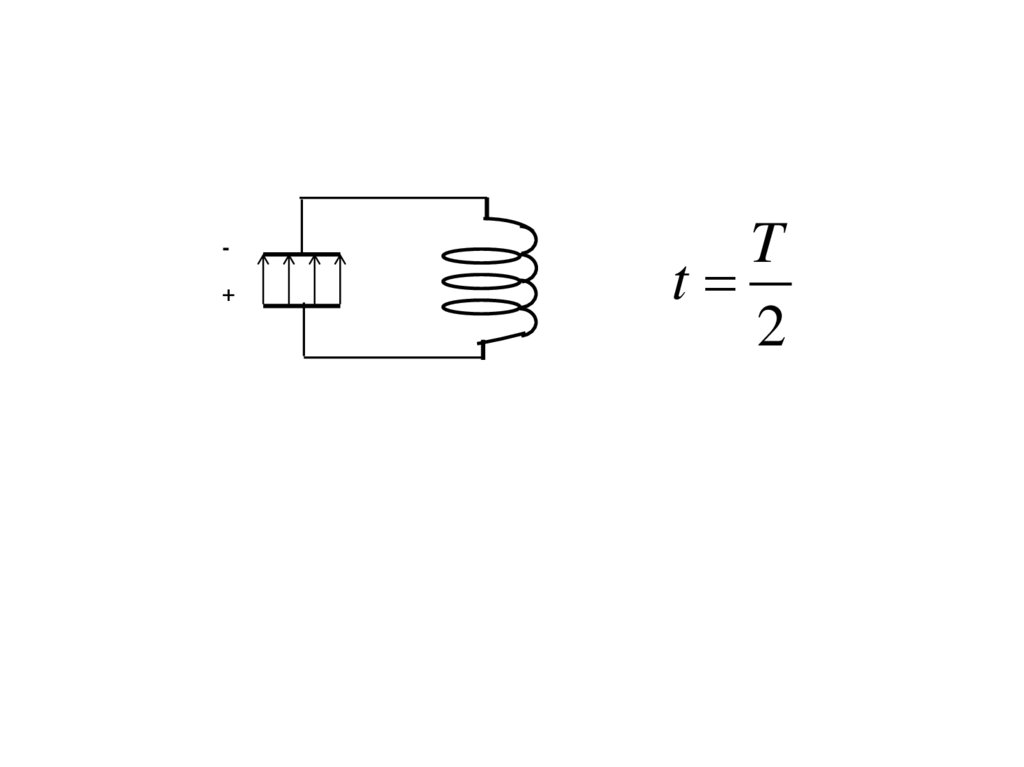
TT
t
4
2
-
+
I
28.
+T
t
2
29.
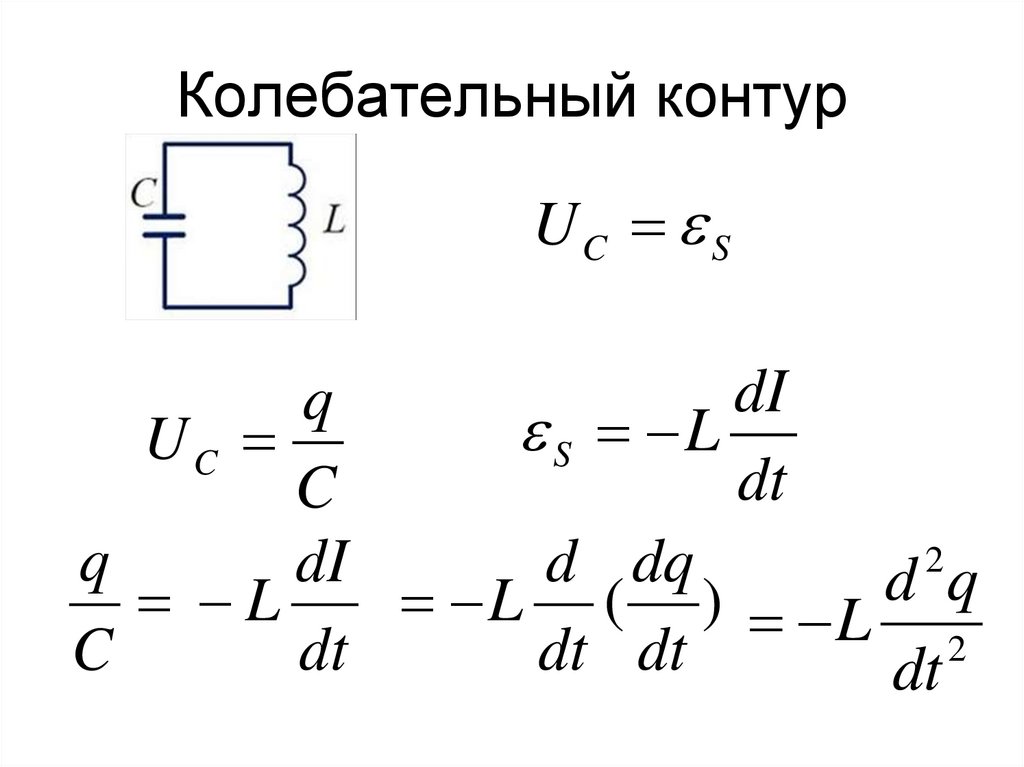
Колебательный контурUC S
dI
q
S L
UC
dt
C
2
q
dI
d dq
L
L ( ) L d q
2
C
dt
dt dt
dt
30.
qq
Lq Lq 0
C
C
1
2
0
LC
q
q
0
LC
q q0 cos( 0t 0 )
q0
U C cos( 0t 0 )
C
dq
I
q0 0 sin( 0t 0 )
dt
31.
dqI
q0 0 sin( 0t 0 )
dt
q0 0 cos( 0t 0 )
2
Колебания тока опережают
колебания напряжения по фазе на π/2
32.
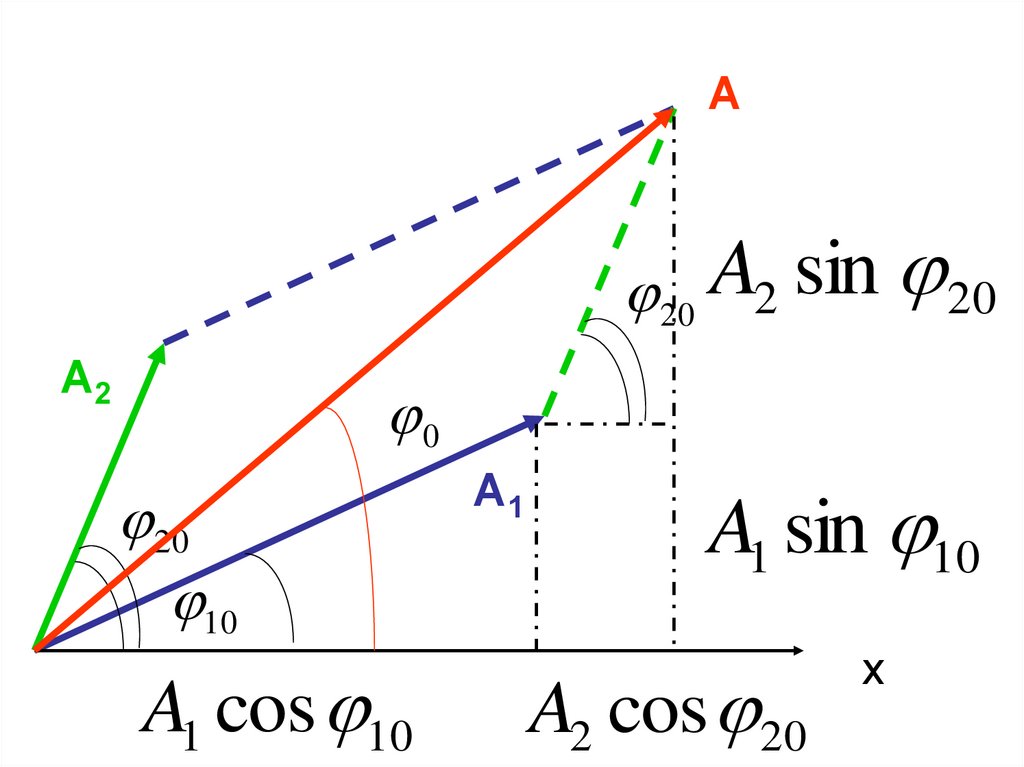
Сложение гармоническихколебаний одного направления
+
x1 A1 cos( 0t 10 )
x2 A2 cos( 0t 20 )
x A cos( 0t 0 )
33.
А20 A2 sin 20
А2
0
20
10
A1 cos 10
А1
A1 sin 10
A2 cos 20
х
34.
tg 0A1 sin 10 A2 sin 20
A1 cos 10 A2 cos 20
A A A2 2 A1 A2 cos( ( 20 10 ))
2
2
1
2
A A2 2 A1 A2 cos( 20 10 )
2
1
2
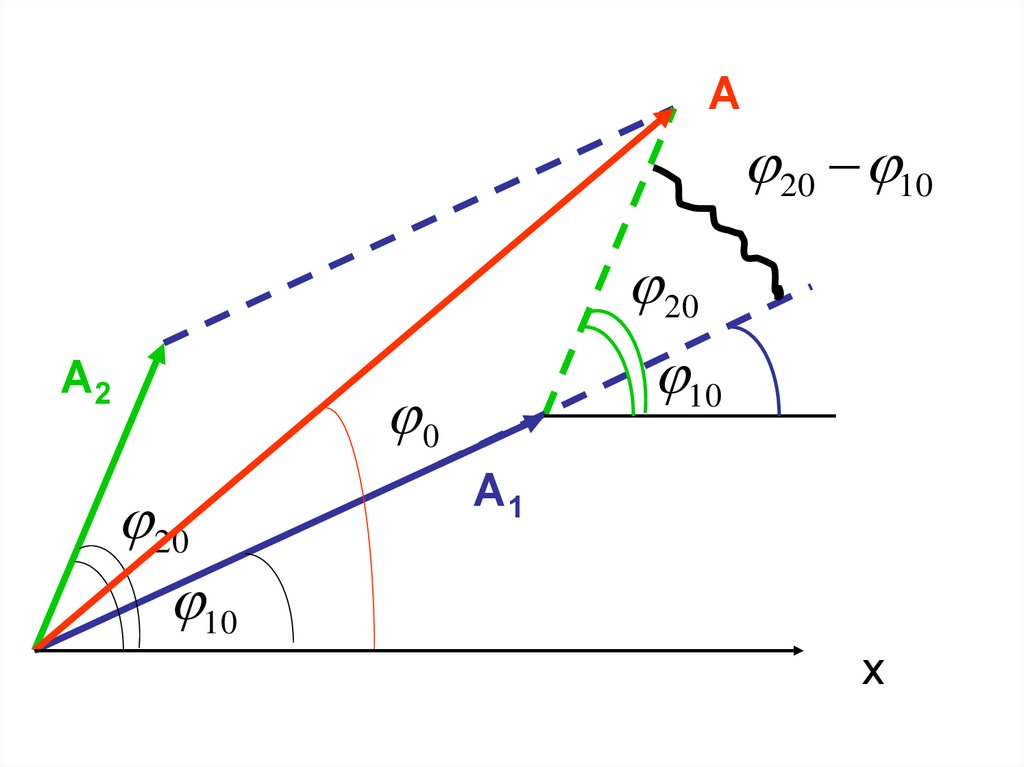
35.
А20 10
А2
20
10
0
20
10
А1
х
36.
20 10 2kA A1 A2 2 A1 A2
2
2
2
A A1 A2
20 10 (2k 1)
A A1 A2 2 A1 A2
2
2
2
A A1 A2
37.
Биения• Рассмотрим 2 гармонических колебания
с одинаковыми амплитудами мало
отличающиеся по частоте
• Начало отсчета выберем так, что
10 0
20 0
38.
+x1 A cos 0t
x2 A cos( 0 )t
x 2 A cos
0t 0t t
2
0t t 0t
cos
2
39.
tx 2 A cos
cos 0t
2
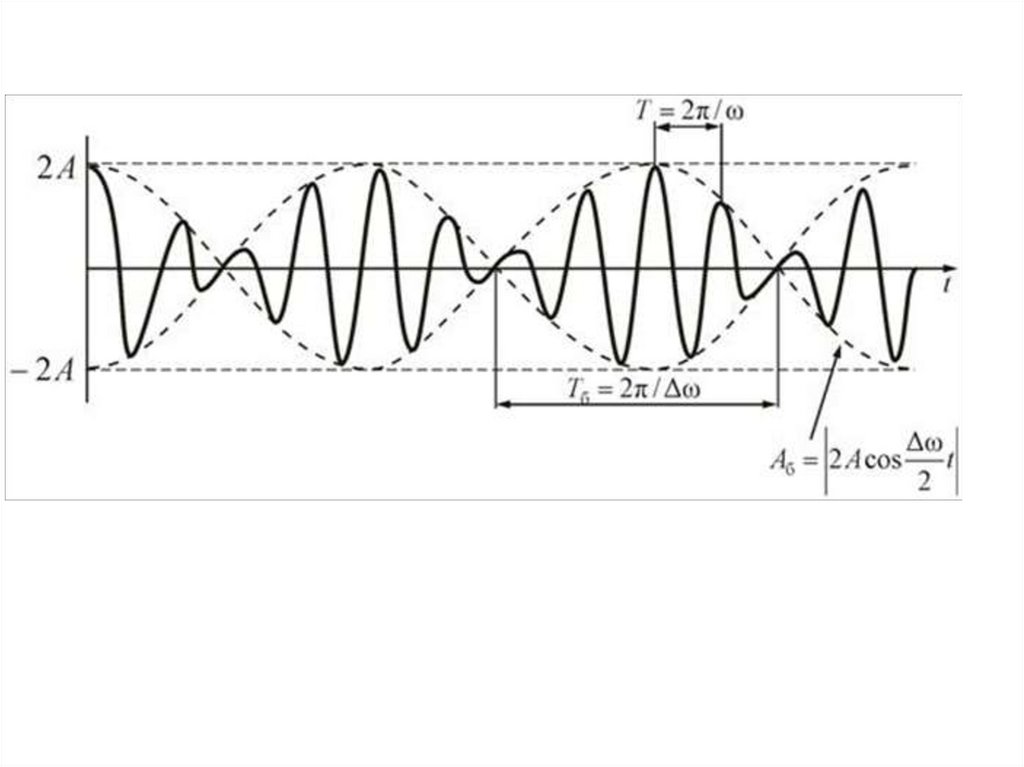
Результирующее колебание – это
колебание с медленно меняющейся
амплитудой
t
AБ 2 A cos
2
40.
41.
Б2
TБ
42.
Сложение взаимноперпендикулярных колебаний
+
x A cos 0t
y B cos( 0t 0 )
x
cos 0t
A
43.
ycos( 0t 0 )
B
cos 0t cos 0 sin 0t sin 0
2
x
x
cos 0 1 2 sin 0
A
A
2
x
y
x
cos 0
1
sin
0
2
A
B
A
44.
2x
y
x
y
2
2
cos
cos
0
0
2
2
A
B
A
B
2
x
2
(1 2 ) sin 0
A
2
2
x
x y
2
y
sin
2
cos
0
0
2
2
A
AB
B
2
Уравнение эллипса
45.
0 mB
y x
A



















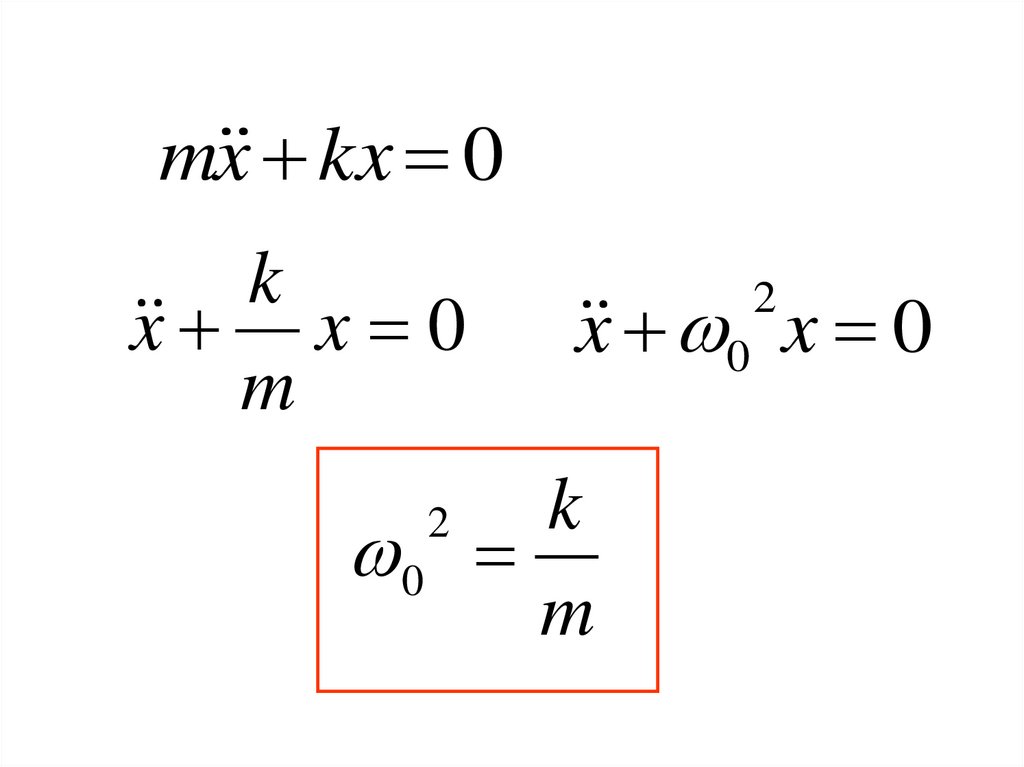
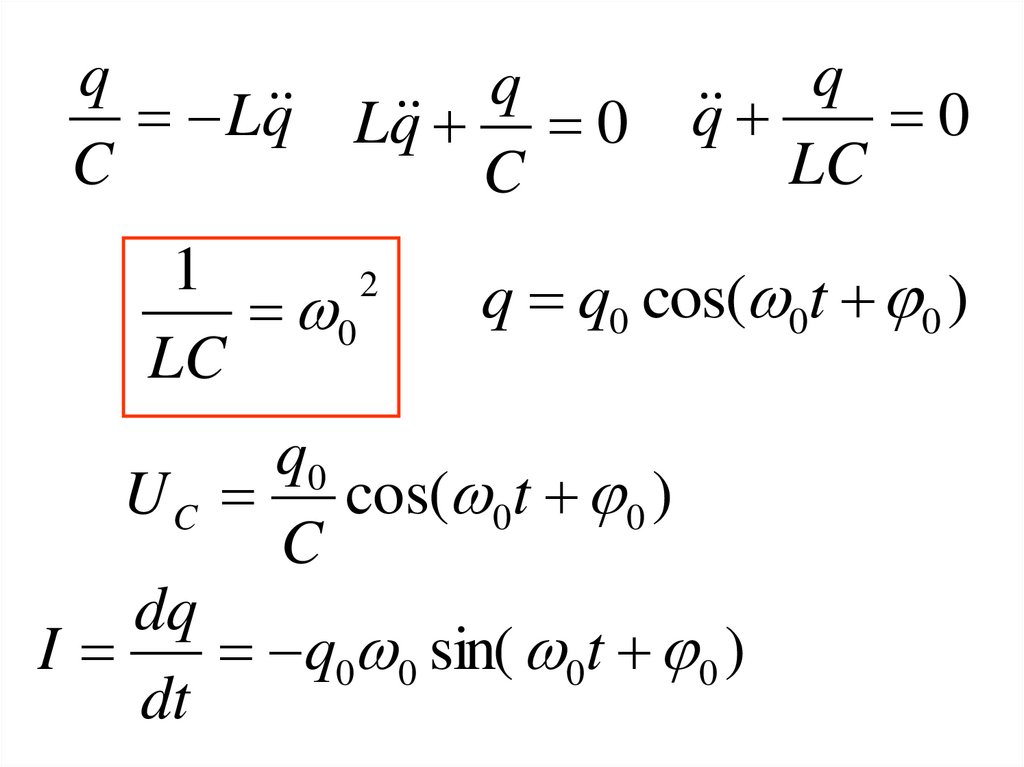


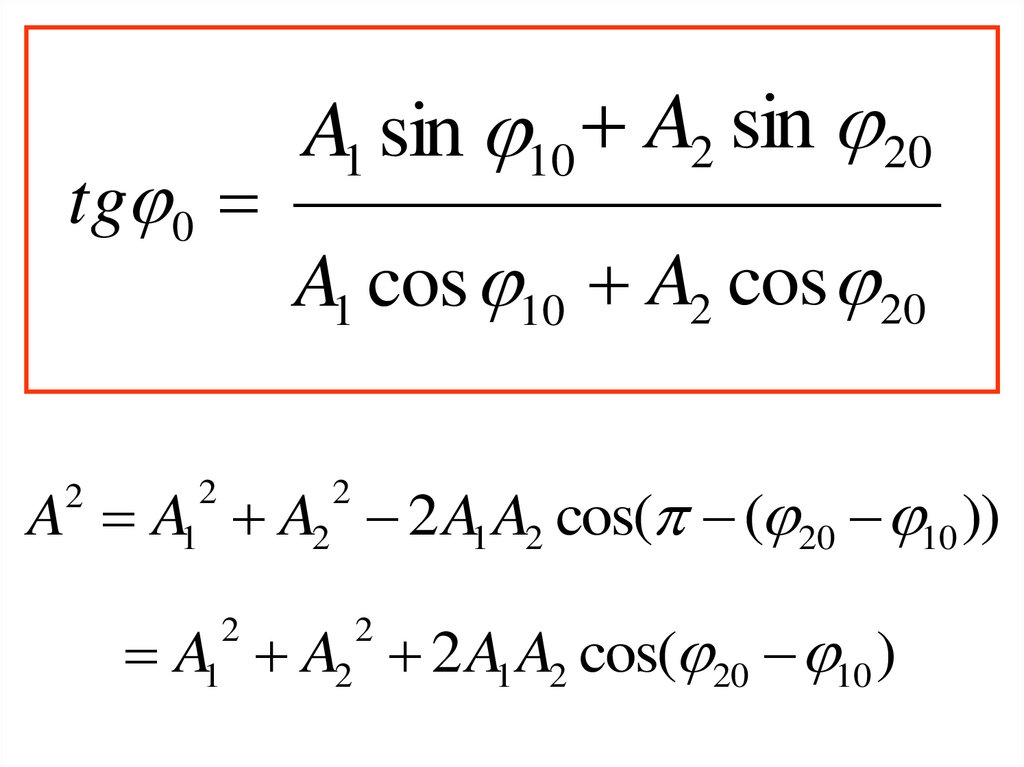
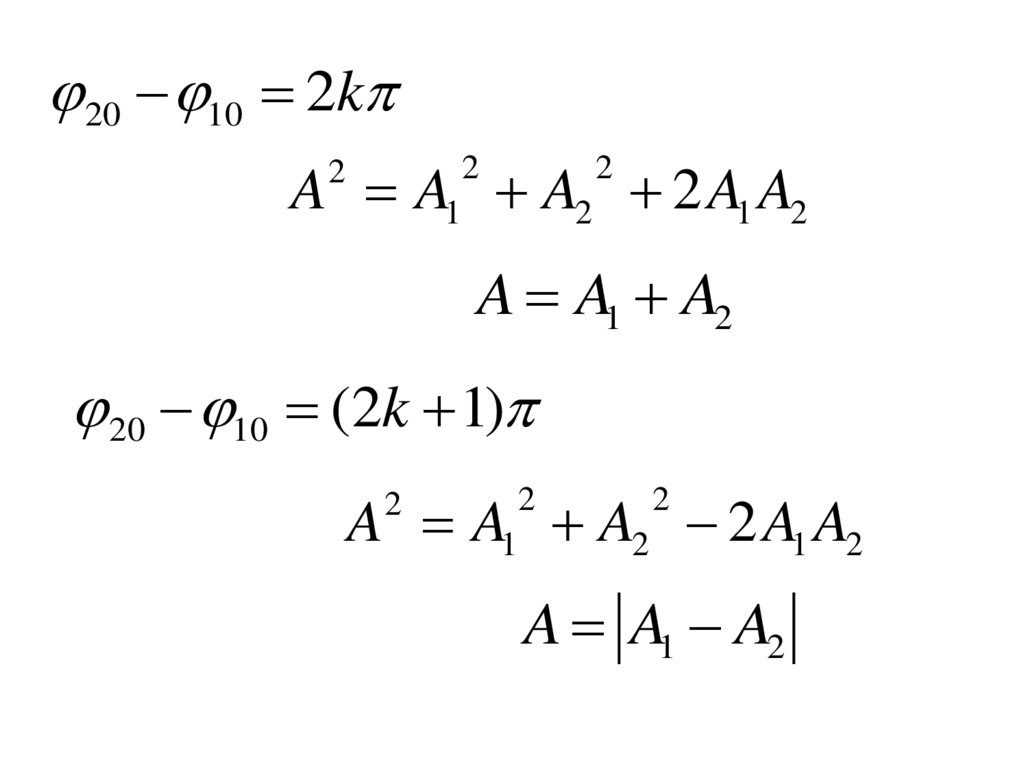

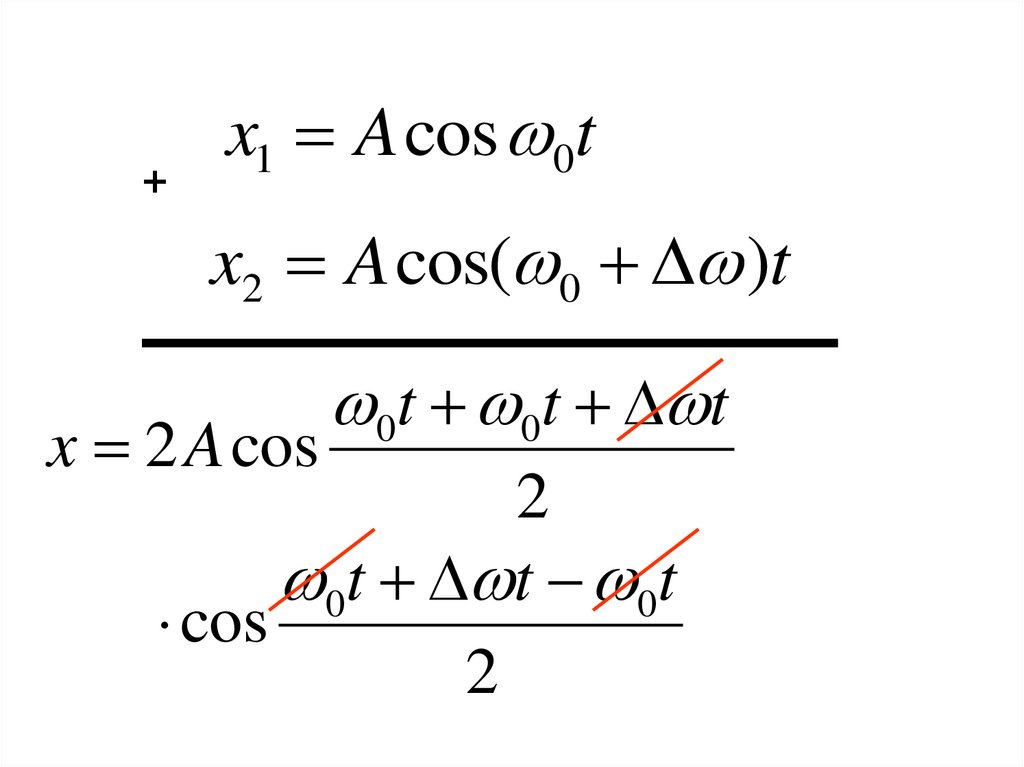

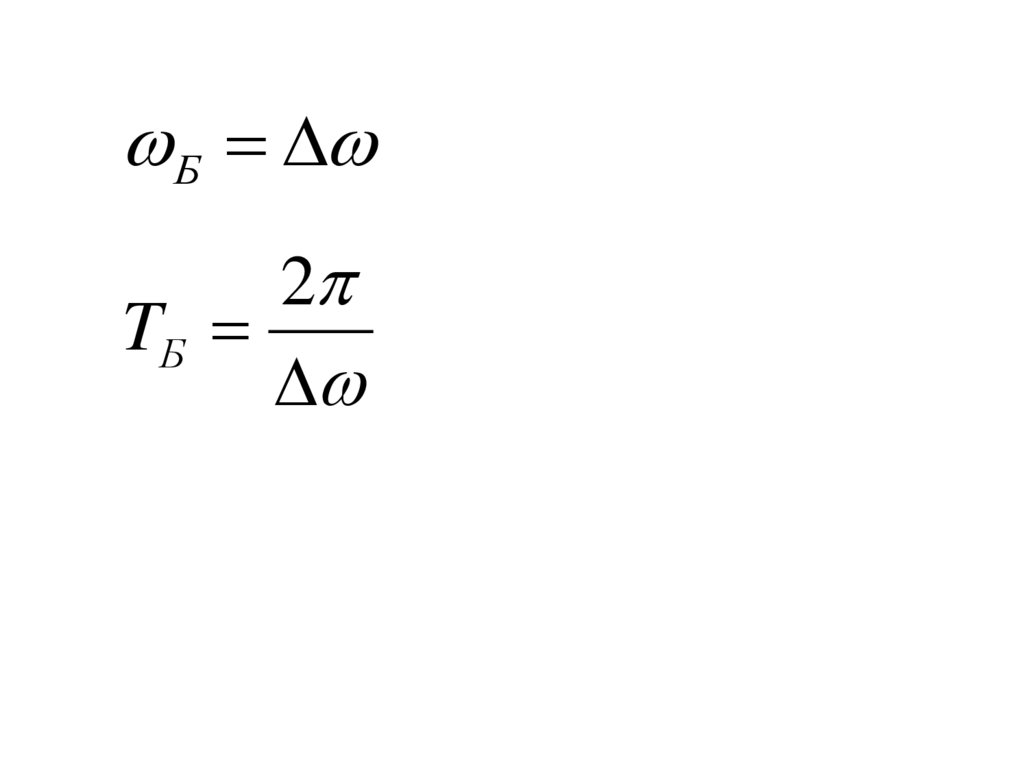

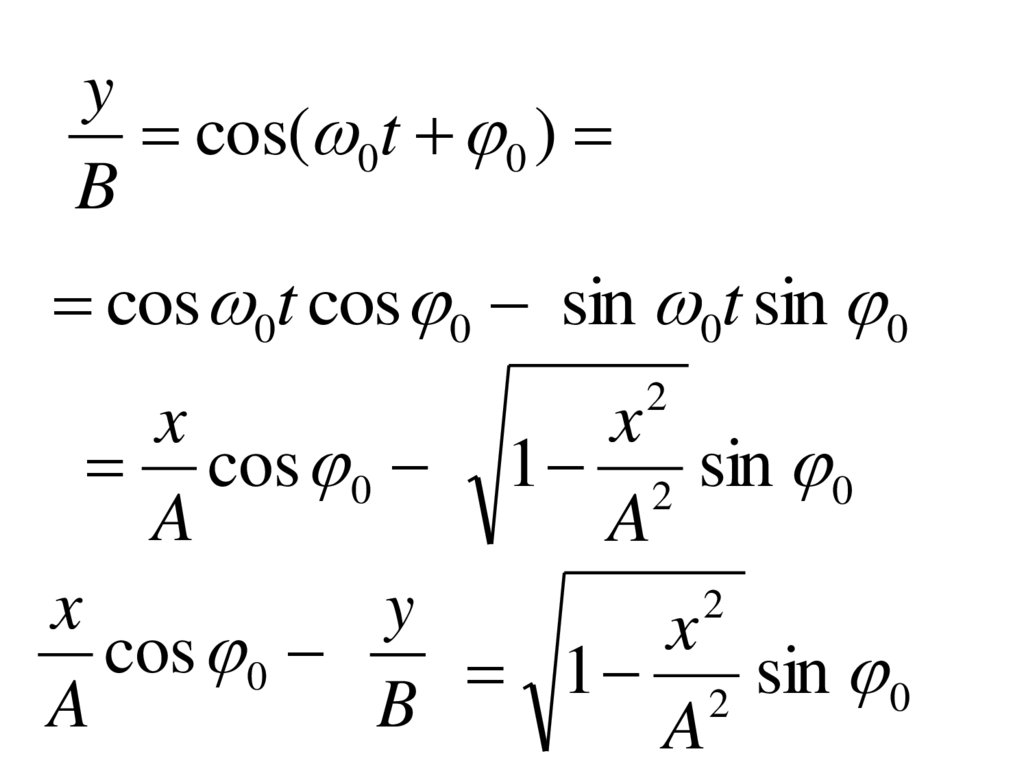
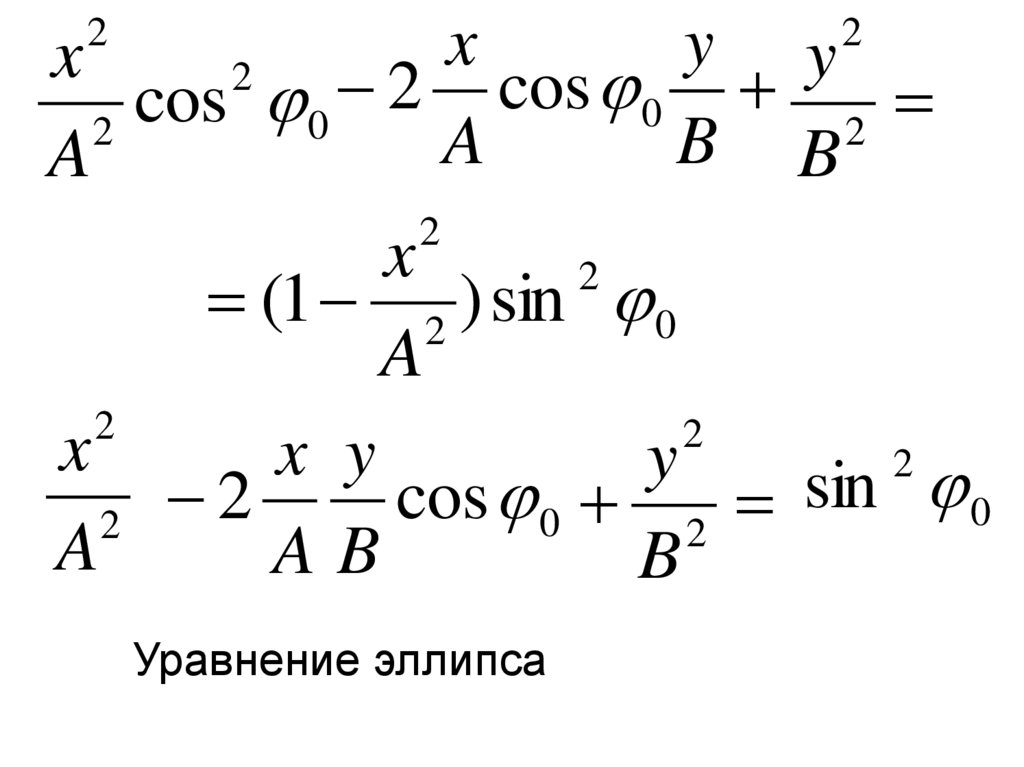
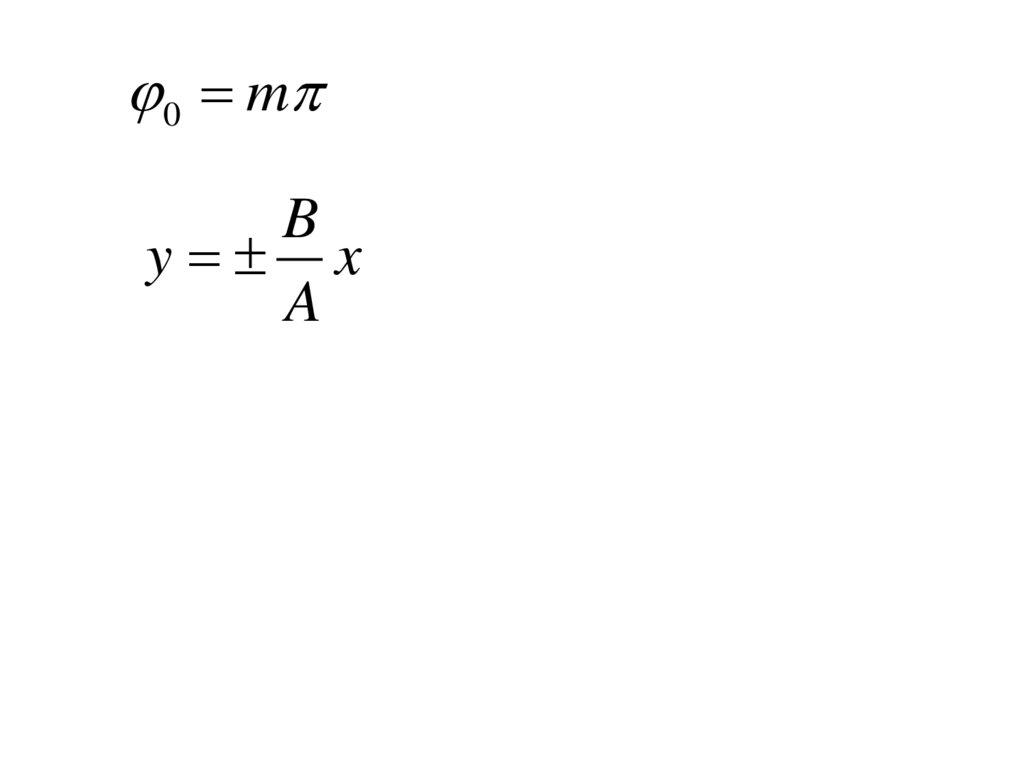
 physics
physics