Гармонические колебания

1.

Сегодня: понедельник, 29 января 2018 г.
Тема 1 ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
1.1 Виды и признаки колебаний
1.2 Параметры гармонических колебаний
1.3 Графики смещения скорости и ускорения
1.4 Основное уравнение динамики гармон. колебаний
1.5 Энергия гармонических колебаний
1.6 Гармонический осциллятор
1

2.

Примеры колебательных процессов
Круговая
волна
на
поверхности
жидкости,
возбуждаемая
точечным
источником (гармонически
колеблющимся шариком).
Генерация акустической
волны громкоговорителем.
2

3.

Примеры колебательных процессов
Поперечная волна в сетке,
состоящей
из
шариков,
скреплённых
пружинками.
Колебания масс происходят
перпендикулярно направлению
распространения волны.
Возможные типы колебаний
атомов в кристалле.
3

4.

В случае абсолютно упругого столкновения шаров (нет
потерь энергии) скорость и угол отклонения крайних
шаров одинаковы, а все промежуточные шары
находятся в покое.
В реальности общая энергия системы со временем
уменьшается за счет трения о воздух, нагревания
шаров, возбуждения акустических волн и т.д.
В результате амплитуда отскока крайних шаров
уменьшается,
а
центральные
шары
начинают
4
совершать колебательные движения.

5.

5

6.

Из приведенного примера следуют три признака
колебательного движения:
повторяемость (периодичность) – движение по
одной и той же траектории туда и обратно;
ограниченность пределами крайних положений;
действие силы, описываемой функцией F = – kx.
6

7.

x A cosφ
Рисунок 2
7

8.

8

9.

9

10.

Колебания называются периодическими, если
значения физических величин, изменяющихся в
процессе колебаний, повторяются через равные
промежутки времени.
• Простейшим типом периодических колебаний
являются
так
называемые
гармонические
колебания.
• Любая колебательная система, в которой
возвращающая сила прямо пропорциональна
смещению, взятому с противоположным знаком
(например, F = – kx), совершает гармонические
колебания.
• Саму такую систему часто называют
10
гармоническим осциллятором.

11.

•Движение от некоторой начальной точки до возвращения
в ту же точку, например от x A к x A и обратно в
x A , называется полным колебанием.
• Частота колебаний ν определяется, как число полных
колебаний в 1 секунду. Частоту, измеряют в герцах (Гц):
• 1 Гц = 1 колеб. в секунду.
1
(1.1.2)
ν
T
• Т – период колебаний – минимальный
промежуток времени, по истечении которого
повторяются значения всех физических величин,
(1.2.3)
характеризующих колебание
2π 1
T
11
ω0 ν

12.

• ω – циклическая (круговая) частота – число
полных колебаний за 2π секунд.
ω0 2 πν
(1.2.2)
• Фаза φ не влияет на форму кривой х(t), а влияет
лишь на ее положение в некоторый произвольный
момент времени t.
• Гармонические колебания являются всегда
синусоидальными.
• Частота и период гармонических колебаний не
зависят от амплитуды.
12

13.

• Смещение описывается уравнением
x Acos (ω0t φ)
тогда, по определению:
(1.2.4)
dx
скорость υ x
ω0 Asin (ω0t φ)
dt
(1.2.5)
dυ x
ускорение ax
ω02 Acos(ω0t φ)
dt
ω0 A υ m
– амплитуда скорости;
2
ω0 A
– амплитуда ускорения.
am
13

14.

1.3 Графики смещения скорости и ускорения
Уравнения колебаний запишем в следующем виде:
x Acos(ω0t φ)
υ x υ m sin( ω0t φ)
a a cos(ω t φ)
m
0
x
Из этой системы
следующие выводы:
уравнений
можно
(1.3.1)
сделать
14

15.

скорость колебаний тела максимальна и равна
амплитуде скорости в момент прохождения через
положение равновесия ( x 0 ).
При максимальном смещении (
скорость равна нулю.
x A )
Ускорение равно нулю при прохождении
телом положения равновесия и достигает
наибольшего
значения,
равного
амплитуде
ускорения при наибольших смещениях.
15

16.

Рисунок 3
16

17.

1.4 Основное уравнение динамики гармонических
колебаний
• Исходя из второго закона, F ma , можно записать
Fx mω02 Acos (ω0t φ) mω02 x
Fx
2
mω 0 x
(1.4.1)
сила F пропорциональна х и всегда направлена к положению
равновесия (поэтому ее и называют возвращающей силой).
Период и фаза силы совпадают с периодом и фазой ускорения.
• Примером сил удовлетворяющих (1.4.1) являются
упругие силы. Силы же имеющие иную природу, но
удовлетворяющие (1.4.1) называются квазиупругими.
(1.4.2)
Квазиупругая сила
F kx,
x
где k – коэффициент квазиупругой силы.
17

18.

d2 x
ax 2
d
t
Получим основное уравнение динамики гармонических
k
2
Сравнивая (1.4.1) и (1.4.2) видим, что ω0
m
колебаний, вызываемых упругими силами:
2
2
2
d x
d x
d x k
m 2 kx или m 2 kx 0 ; 2 x 0, тогда
m
dt
dt
dt
2
d x
2
ω
x
0
0
2
dt
Основное уравнение
динамики гармонических
колебаний
Решение этого уравнения всегда будет выражение вида
x Acos (ω0t φ)
18

19.

Круговая частота колебаний
но
2
ω0
k
m
Период колебаний
2π
ω0
T
2π
k
тогда T
m
m
T 2π
k
x A cosφ
19

20.

1.5 Энергия гармонических колебаний
Рисунок 1
Потенциальная энергия тела U, измеряется той работой,
которую произведет возвращающая сила Fx kx
20

21.

x
dU
Fx
; dU Fdx kxdx, отсюда U k xdx или
dx
0
•Потенциальная
2
kx
1 2 2
энергия
U
kA cos (ω0t φ)
2
2
(1.5.1)
•Кинетическая энергия
mυ
1
2 2
2
K
mω0 A sin (ω0t φ)
2
2
2
(1.5.2)
• Полная энергия:
1
1
1 2 (1.5.3)
2 2 , или
2 2
E U K mω0 A
E mω0 A kA
2
2
2
Полная механическая энергия гармонически колеблющегося
21
тела пропорциональна квадрату амплитуды колебания.

22.

Колебания груза под действием сил тяжести
Максимум потенциальной энергии, (из 1.5.1)
U max
1 2
mgh kA
2
Максимум кинетической энергии
mυ
1 2
kA
2
2 22
2
K max
но когда K max , U 0 и наоборот.

23.

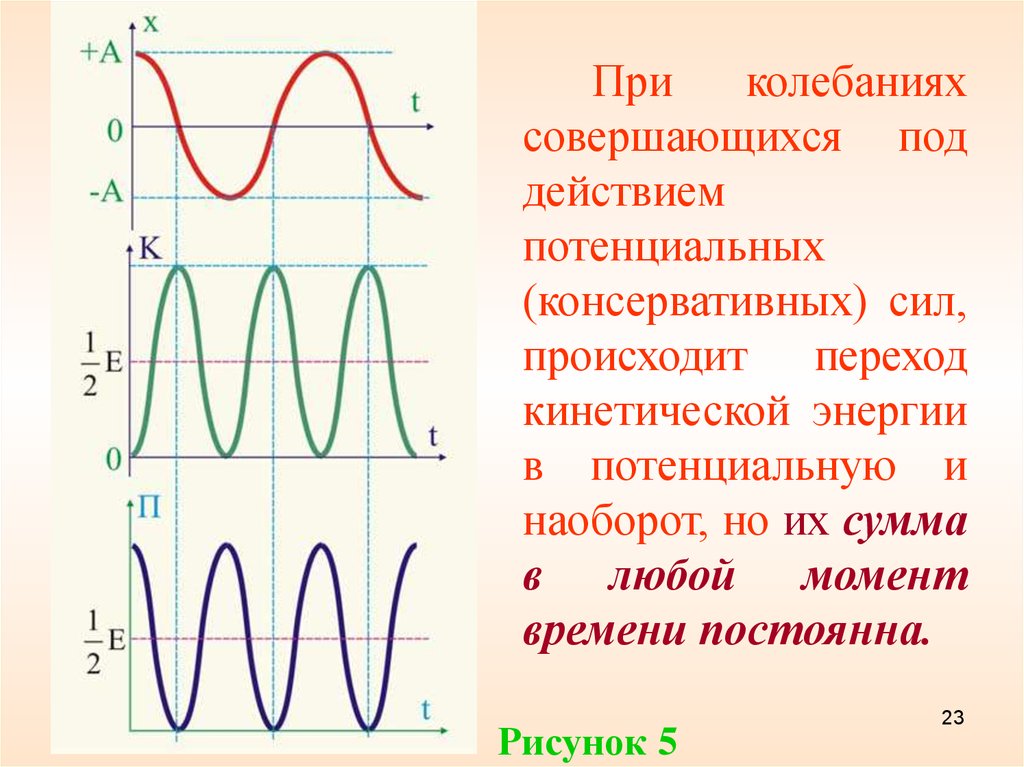
При
колебаниях
совершающихся под
действием
потенциальных
(консервативных) сил,
происходит переход
кинетической энергии
в потенциальную и
наоборот, но их сумма
в любой момент
времени постоянна.
Рисунок 5
23

24.

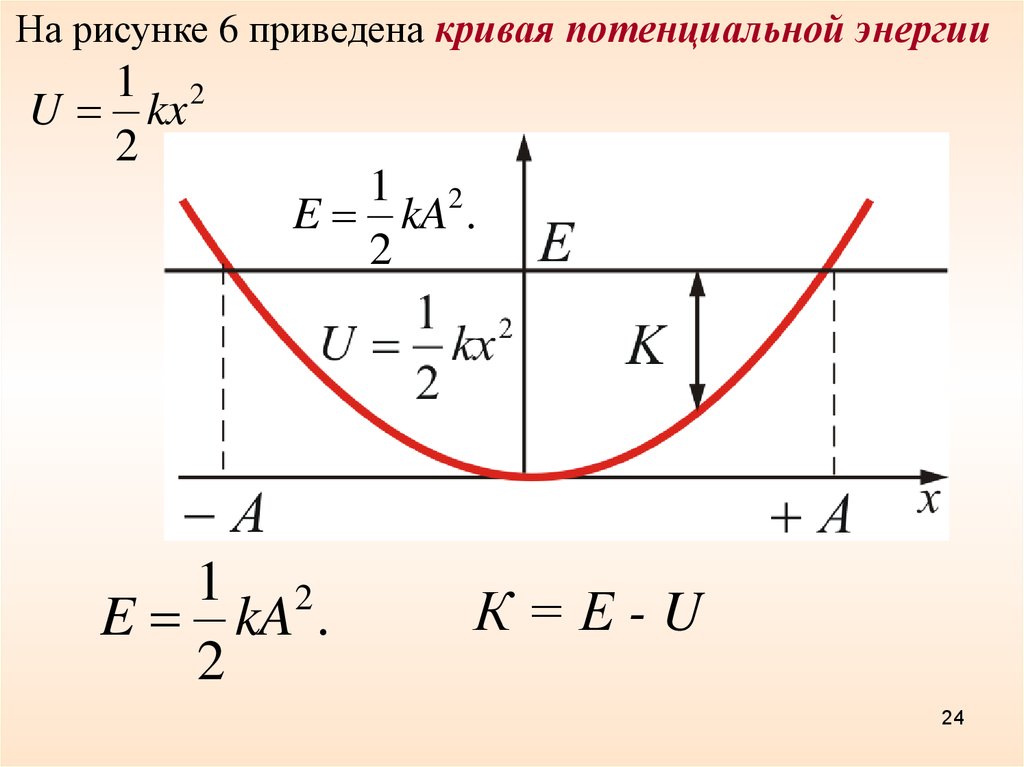
На рисунке 6 приведена кривая потенциальной энергии
1 2
U kx
2
1 2
E kA .
2
Рисунок 6
1 2
E kA .
2
К=Е-U
24

25.

1.6 Гармонический осциллятор
1. Пружинный маятник –
это
груз
массой
m,
подвешенный
на
абсолютно
упругой
пружине с жесткостью k,
совершающий
гармонические колебания
под действием упругой
силы F kx
Рисунок 7
25

26.

Из второго закона Ньютона F = mа; или F = - kx
получим уравнение движения маятника:
2
d x
m 2 kx
dt
или
d 2x k
x 0
2
dt
m
(1.6.1)
Решение этого уравнения – гармонические колебания вида:
x A cos( ω0t φ)
циклическая частота ω
k
ω0
;
m
период Т
m
T 2π
k
26

27.

2 Математическим маятником –
называется идеализированная система,
состоящая из невесомой, нерастяжимой
нити, на которую подвешена масса,
сосредоточенная в одной точке (шарик
на длинной тонкой нити).
ω0
g
l
l
T 2π
g
-собственная
частота
-период колебаний
математического
маятника
27

28.

3 Физический маятник – это
твердое тело, совершающее под
действием силы тяжести
колебания вокруг неподвижной
горизонтальной оси, проходящей
через точку подвеса D, не
совпадающую с центром масс С
l – расстояние между точкой
подвеса и центром инерции
маятника D-С.
J – момент инерции маятника относит. точки подвеса28D.

29.

2
ω0
mgl
J
J
lпр.
ml
J
T 2π
mgl
T 2π
lпр.
g
lпр. – приведенная длина физического маятника – это длина такого
математического маятника, период колебания которого совпадает с
периодом колебаний данного физического маятника.
29

30.

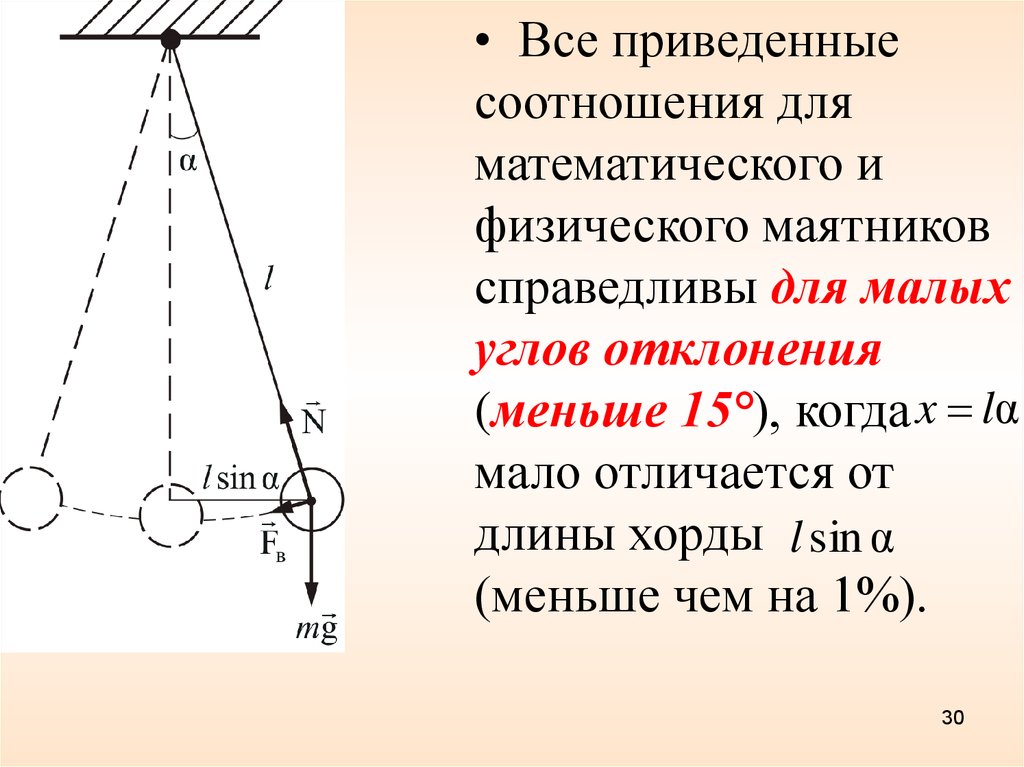
• Все приведенные
соотношения для
математического и
физического маятников
справедливы для малых
углов отклонения
(меньше 15°), когда x lα
мало отличается от
длины хорды l sin α
(меньше чем на 1%).
30

31.

3.1 Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия
механических колебаний постепенно расходуется на работу против
сил трения и амплитуда колебаний уменьшается.
Сила трения (или сопротивления)
Fтр rυ
где r – коэффициент сопротивления,
– скорость движения
υ

32.

32

33.

Второй закон Ньютона для затухающих прямолинейных
колебаний вдоль оси x
ma x kx rυ x
где kx – возвращающая сила,
– сила трения.
r
x
2
d x r dx k
x 0
2
m dt m
dt
Введем обозначения
k
ω02
m
r
β;
2m
2
d x
dx
2
2β ω0 x 0
2
dt
dt
Решение уравнения (3.1.1) имеет вид (при
β ω 0)
(3.1.1)

34.

Решение уравнения (3.1.1) имеет вид
x A0e
βt
(3.1.2)
cos( ωt φ)
Найдем частоту колебаний ω.
(ω ω0 )
2
2
β
ω
0
ω ω β
0
k
ω0
m
;
r
β
2m
период-
2
;
k r
ω
.
m 2m
2π
2π
T
,
2
2
ω
ω0 β

35.

Логарифмическим
декрементом
затухания
называется
натуральный логарифм отношения амплитуд, следующих друг за
другом через период Т.
A(t )
βT
χ ln
ln e βT;
A(t T )
A0
βτ
1 откуда
e e ,
Aτ
βτ 1;
χ βT
1
β .
τ
Следовательно, коэффициент затухания β – есть физическая
величина, обратная времени, в течение которого амплитуда
уменьшается в е раз,
τ – время релаксации.

36.

χ βT
1
β .
τ

37.

Когда сопротивление становится равным критическому
r rкр , а β ω0 , то круговая частота
обращается в нуль (
ω 0), ( T ), колебания
прекращаются. Такой процесс называется апериодическим:
r rкр
β ω0
ω 0
T
Рисунок 2

38.

Отличия в следующем.
При колебаниях, тело, возвращающееся в
положение равновесия, имеет запас кинетической
энергии. В случае апериодического движения
энергия тела при возвращении в положение
равновесия оказывается израсходованной на
преодоление сил сопротивления трения.

39.

3.3 Вынужденные механические колебания
Рассмотрим систему, на которую кроме упругой силы (– kx) и сил
сопротивления (– rυ) действует добавочная периодическая сила F –
вынуждающая сила:
ma x kx rυ x Fx
– основное уравнение колебательного процесса, при вынужденных
колебаниях
2
d x
dx
2
2β ω0 x Fx
2
dt
dt
Fx F0 cos ωt.
(3.3.1)

40.

F0
A
m
2
(ω0
ω ) 4β ω
2 2
2
2
Проанализируем выражение
1) ω 0 (частота вынуждающей силы равна нулю)
x F0 / mω02
– статическая амплитуда, колебания не совершаются.
β 0 (затухания нет). С увеличением ω (но при
ω ω0), амплитуда растет и при
ω ω0 , амплитуда
резко возрастает (
А ). Это явление называется
– резонанс. При дальнейшем увеличении (
ω ω0 )
2)
амплитуда опять уменьшается. (Рисунок 4 )
3)
β 0. ωрез
2
ω0
2β
2 – резонансная частота

41.

ω ω0
А
- явление резонанса
Рисунок 4
ωрез
2
ω0
2 – резонансная частота
2β

42.

ωрез
2
ω0
2β
2 – резонансная частота.
Явление возрастания амплитуды вынужденных колебаний при
приближении частоты вынуждающей силы к
называется
резонансом.
ωрез
β 0, ωрез ω0
Для консервативной системы, т.е.
для диссипативной
частоты .
ω рез меньше собственной круговой
несколько
ω0
С увеличением коэффициента затухания β явление
резонанса проявляется все слабее и исчезает при
ω0
β
2