Similar presentations:
Сложение колебаний Сложение гармонических колебаний одного направления и одинаковой частоты
1. Сложение колебаний
2.
Сложение гармонических колебаний одногонаправления и одинаковой частоты:
х1 = А1 cos ( t + 1), х2 = А2 cos ( t + 2).
Результирующее колебание х = х1 + х2 должно
быть гармоническим колебанием той же
частоты , что и складываемые колебания, то
есть х = А cos ( t + ). Задача заключается в
нахождении амплитуды А и начальной фазы
результирующего колебания.
3.
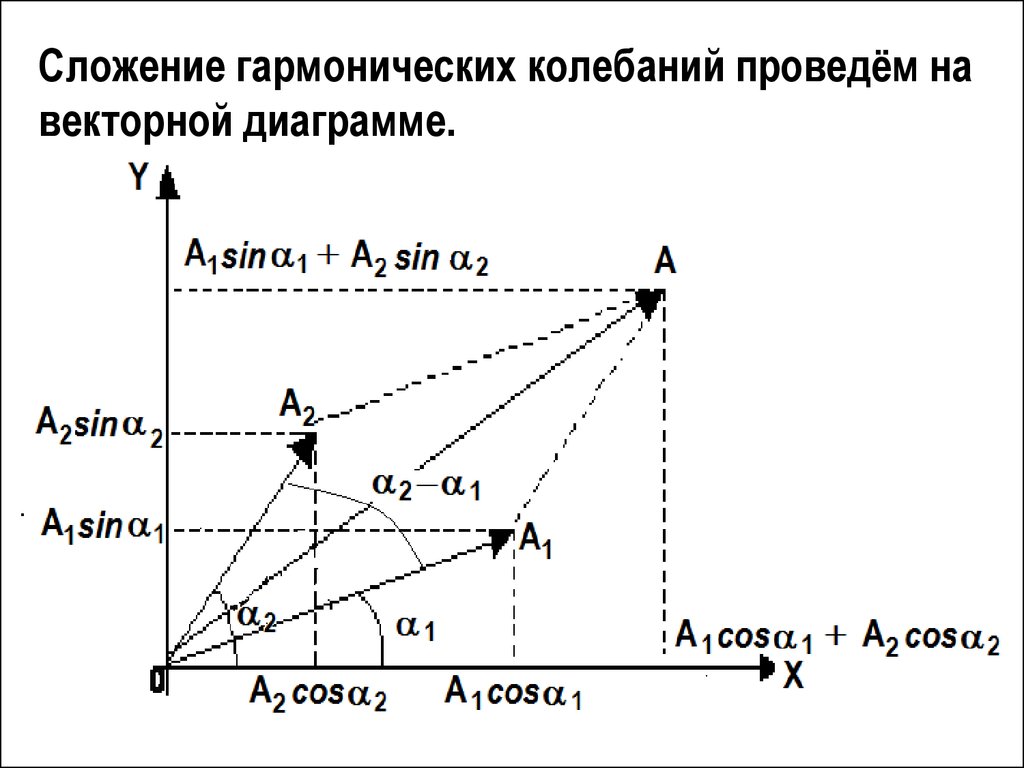
Сложение гармонических колебаний проведём навекторной диаграмме.
4.
Результирующий вектор, определяемый поправилу параллелограмма, будет изображать
результирующее колебание х = х1 + х2.
Амплитуду А результирующего колебания
определим из векторной диаграммы по теореме
косинусов:
и начальную фазу из
5.
Амплитуда результирующего колебанияполучается наибольшей (А = Амакс) при их
синфазности, т. е. при разности фаз кратной
чётному числу :
Амакс = А1 + А2 при 2 - 1 = 2m ;
6.
При разности фаз складываемых колебанийкратной нечётному числу они оказываются в
противофазе, и амплитуда результирующего
колебания получается минимальной.
Амин = А1 - А2 при 2 - 1 = (2m + 1) ; m = 0, 1, 2, …
7.
При равенстве амплитуд А1 = A2 складываемыхколебаний амплитуда результирующего
колебания становится равной нулю.
Противофазные колебания с равными
амплитудами полностью погашают друг друга.
8.
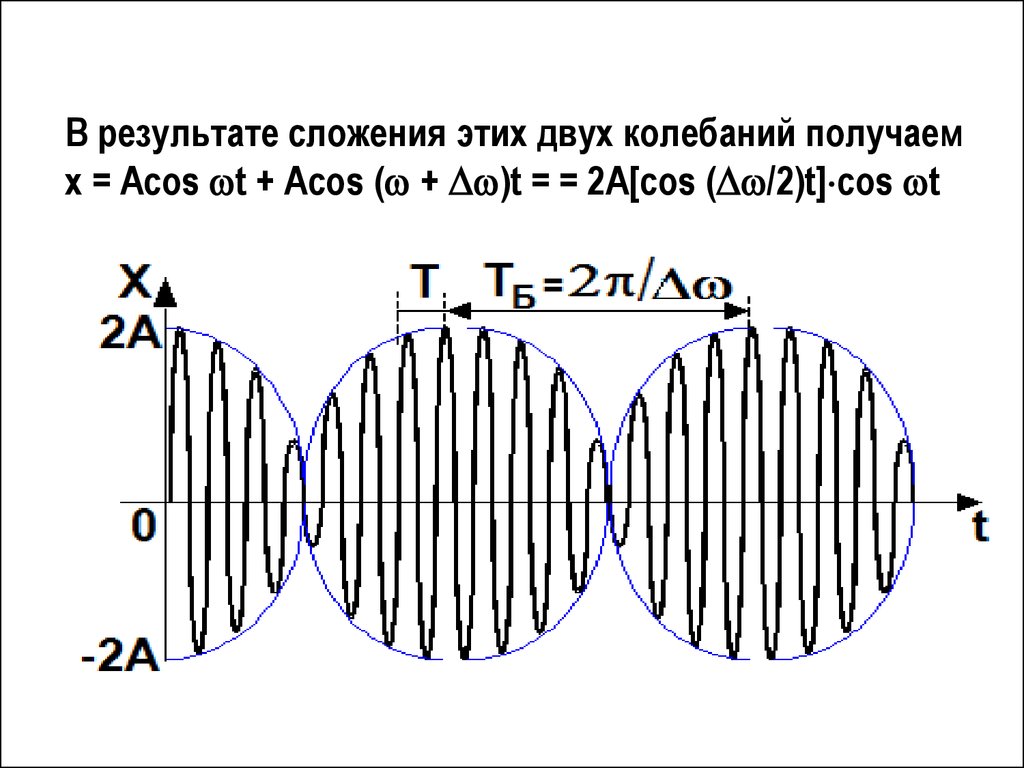
БИЕНИЯх1 = А1cos ( t + 1)
х2 = А1cos ( + )t + 2)], где .
Результирующий вектор с амплитудой А = А1 + A2
будет при этом пульсировать по величине (по
модулю) и вращаться с переменной скоростью.
9.
В результате сложения этих двух колебаний получаемх = Аcos t + Аcos ( + )t = = 2А[cos ( /2)t] cos t
10.
Биениями называют периодические измененияамплитуды результирующего колебания от
сложения двух однонаправленных колебаний с
близкими частотами: - частота биений.
11.
Сложение перпендикулярных колебаний.Задача нахождения траектории
результирующего движения заключается в
исключении параметра t и связывании
напрямую координат у и х.
12.
После необходимых математическихпреобразований (выразить косинус суммы
аргументов, найти чему равны sin t и cos t)
получаем уравнение эллипса с произвольной
ориентацией его осей относительно осей Х и У.
13.
Частные случаи:а) = 0 (или 2 m) - колебания по х и у синфазны:
б) = (2m + 1) - колебания по х и у
противофазны.
Траектория – прямая линия.
В
-А
0
-В
Y
=0
А Х
=
14.
в) = 2 - колебания по х и у фазно-ортогональны.Уравнение траектории: х2 А2 + у2/В2 = 1 - уравнение
эллипса приведённого к осям координат.
При равенстве амплитуд складываемых взаимноперпендикулярных колебаний эллипс вырождается
в окружность.
У
Случаи = /2 и = В
R
/2 отличаются
направлением
0
-А -В
0 В А Х
движения точки по
эллипсу или
-В
окружности (по или
против часовой стрелки).
15.
Фигуры Лиссажу.Частоты взаимно перпендикулярных
колебаний не
одинаковы. При
кратности частот
траектория становится
замкнутой, причём
число пересечения ею
осей Х и Y повторяет
соотношение частот
соответствующих колебаний.
16.
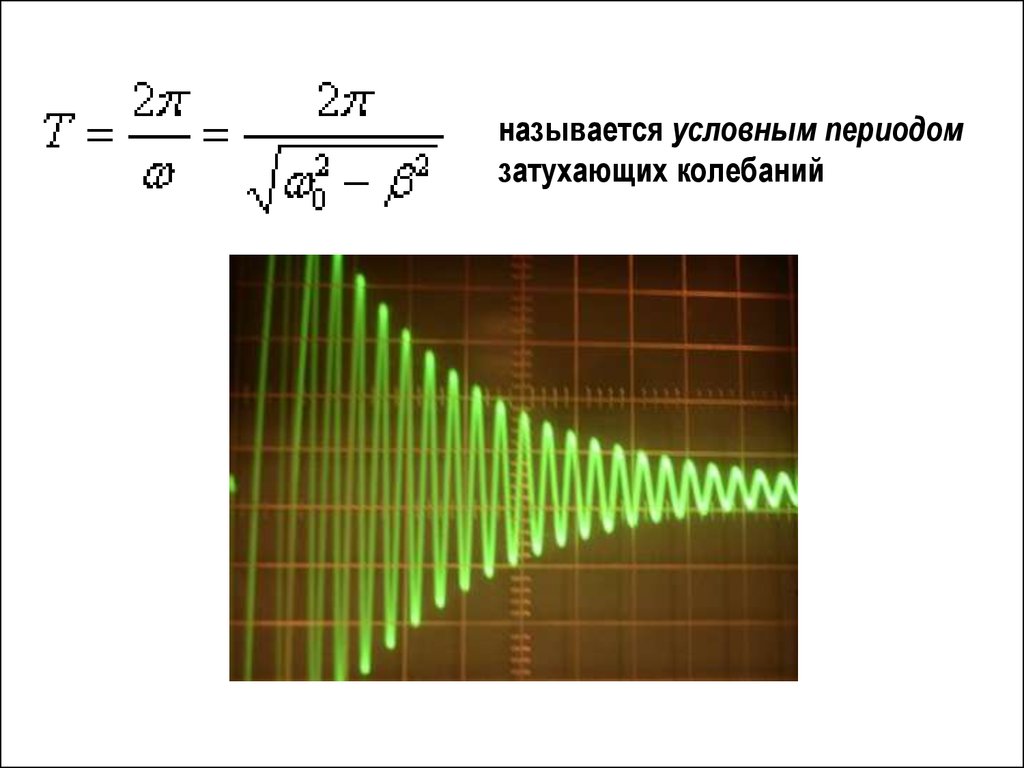
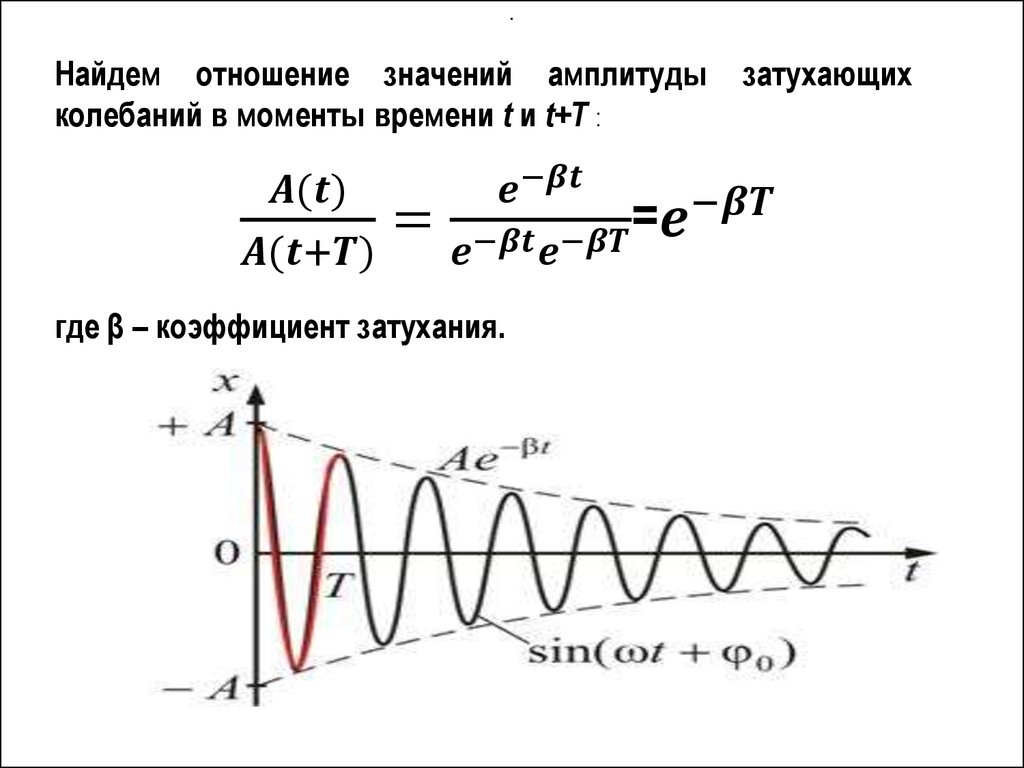
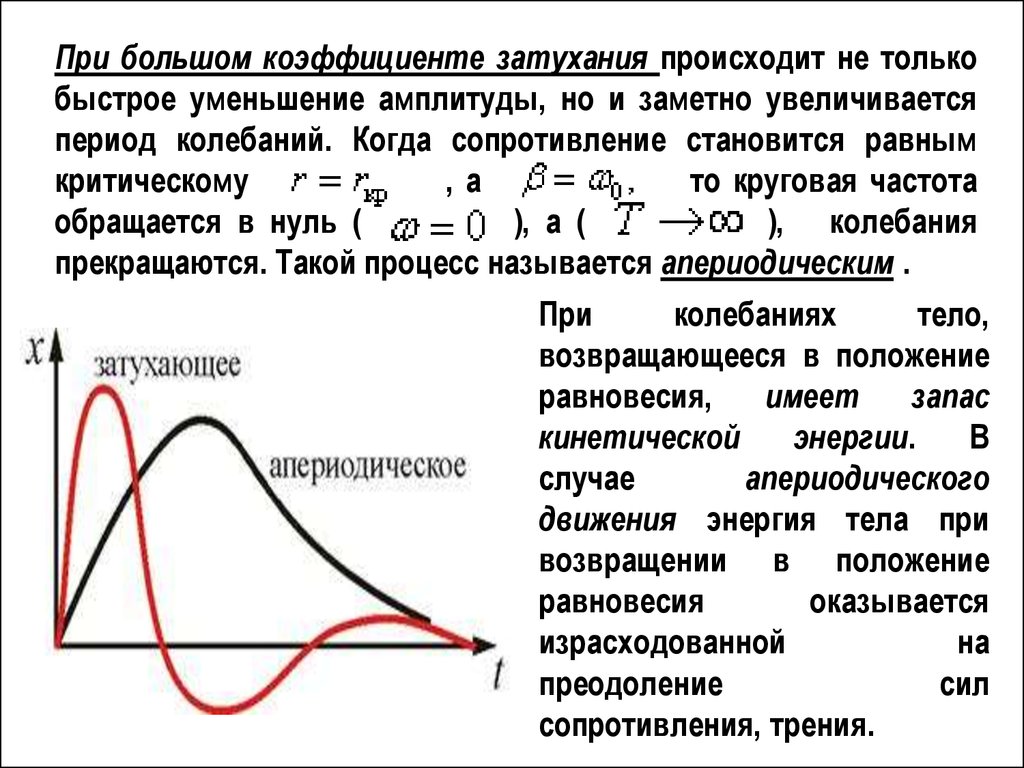
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ17.
.Сила трения (или сопротивления)
























 physics
physics








