Similar presentations:
Общие вопросы математического описания электромеханических систем
1. Динамические процессы в электроприводе
ЛЕКЦИЯ 1ОБЩИЕ ВОПРОСЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ
ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ
2. Энергетический подход к описанию электромеханических систем
Изучение электромеханических систем должно решить три главные задачи:1) физическое описание системы
2) составление дифференциальных уравнений движения системы
3) решение уравнений с учетом конкретных условий задачи
План получения управлений движения
1. Повторение основных соотношений электромеханики
2. Анализ запасенной энергии системы
- с учетом механических сил в магнитном поле
- с учетом механических сил в электрическом поле
3. Фундаментальные соотношения в электромеханике
Уравнение динамического равновесия для k-го механического узла:p
i 1
где
f ki 0
ki
dpki d
pki
mki xki – инерционная сила i-го узла, а mki – масса, xki – перемещение
dt
dt
fki – механическая сила, включая любые силы связи, приложенная к i-му узлу
Принцип Даламбера из соотношения непрерывности пространства и законы Кирхгоффа:
x
где
i 1
ki
0
e
i 1
ki
0
eki – напряжение в k-м контуре, iki – i-й ток в k-м узле
i
i 1
ki
0
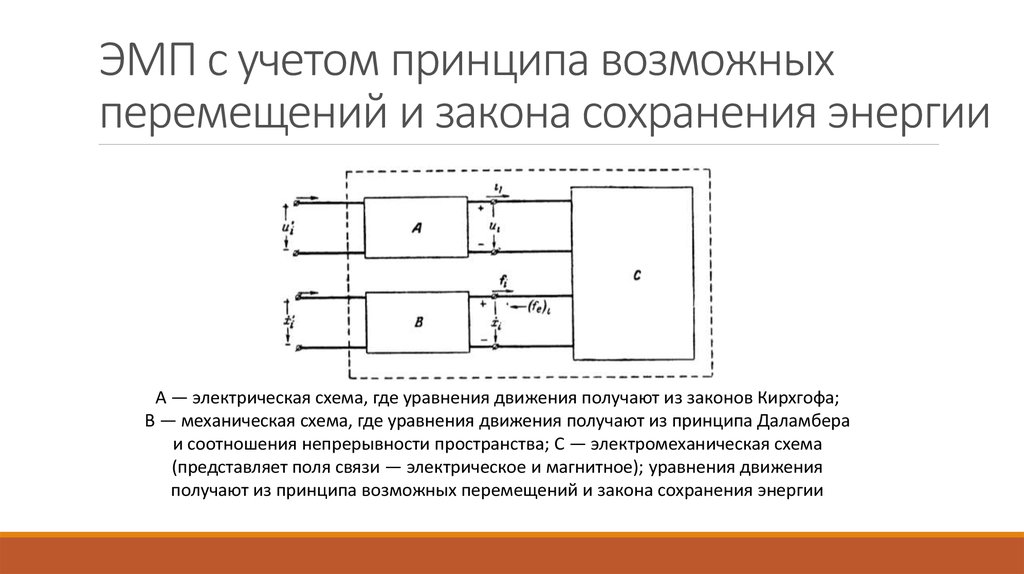
4. ЭМП с учетом принципа возможных перемещений и закона сохранения энергии
А — электрическая схема, где уравнения движения получают из законов Кирхгофа;В — механическая схема, где уравнения движения получают из принципа Даламбера
и соотношения непрерывности пространства; С — электромеханическая схема
(представляет поля связи — электрическое и магнитное); уравнения движения
получают из принципа возможных перемещений и закона сохранения энергии
5. Консервативная электромеханическая связанная схема
Полная накопленная энергияСвязь с накопителем энергии
электрического поля
Связь с накопителем
энергии магнитного поля
W=We+Wm
где
We – энергия, запасенная в электрических полях
Wm – энергия, запасенная в магнитных полях
Электрические и магнитные переменные связаны:
l
qk Cki ui k
i 1
ik
dqk
dt
uk
n
L i
i l 1
d k
dt
ki i
6. Ограничения на электромеханическую систему
1.Параметры должны быть сосредоточенные. Они вычисляются в общем случае из
электромагнитных полей
2.
Должны быть однозначными следующие зависимости:
uk uk q1 ,
, ql , x1 ,
, xm
qk qk u1 ,
, ul , x1 ,
, xm
k k il 1 , , in , x1 , , xm
ik ik l 1 ,
f k f k q1 ,
3.
, n , x1 ,
, ql , l 1 ,
, xm
, n , x1 ,
, xm
Гистерезис не учитывается, но потери от гистерезиса могут быть учтены при помощи
активного сопротивления, вынесенного за пределы связанной системы
7. Энергии, вовлекаемые в возможное перемещение
Энергия, поступающая на электрические зажимы:n
u i dt
i 1
i i
Энергия, поступающая на механические зажимы:
f e k xk dt f e k dxk
Отсюда, согласно закона сохранения энергии, получим изменение запасенной энергии:
n
dW ui ii dt f e k dxk
i 1
Это даст нам уравнение для силы электромеханической связи:
f e k
1 n
u
i
dt
dW
ii
dxk i 1
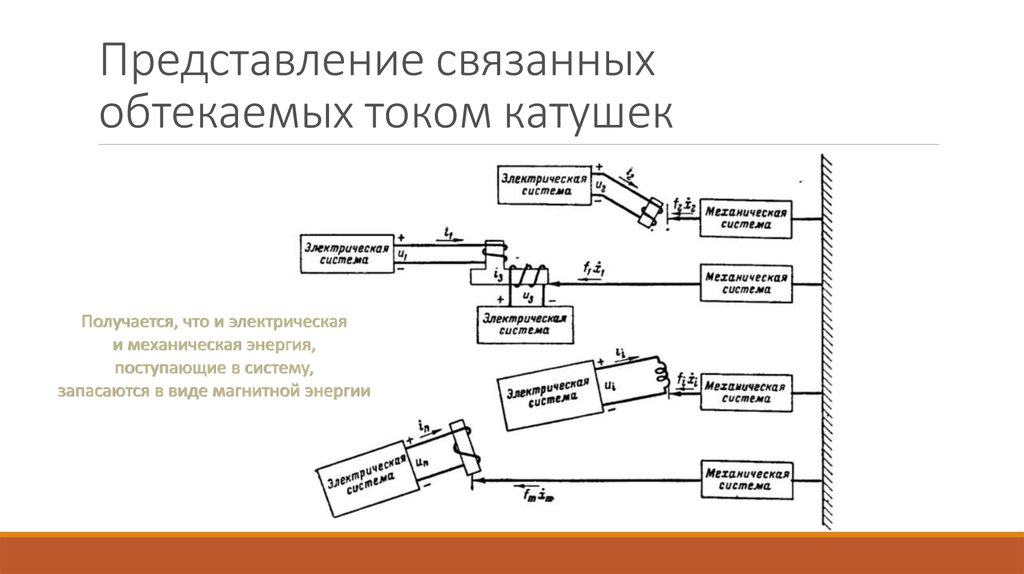
8. Представление связанных обтекаемых током катушек
Получается, что и электрическаяи механическая энергия,
поступающие в систему,
запасаются в виде магнитной энергии
9. Запасенная энергия в магнитных полях для определения силы
Запасенная магнитная энергия:Wm 1 ,
, n , x1 ,
, xm
1 , , n n
i ,
0, ,0
где
i 1
i
1
, n , x1 ,
, xm d i
ii´и Ψi´ – токи и потокосцепления для некоторого фиксированного положения системы,
для которого xj=const
С другой стороны изменения запасенной магнитной энергии с учетом связи ii и Ψi:
n
Wm
W
dWm i1 , , in , x1 , , xm
dxk m dii
xk
i 1 ii
Тогда из уравнения для силы электромеханической связи получим:
n
n
n i
Wm
i
Wm
di
f
dx
i
d
dW
i
dx
i
dx
dii
e k k i i
r
m
i
k
i
k
xk
i 1
i 1
i 1 r 1 ir
i 1 ii
xk
n
n
10. Запасенная энергия в магнитных полях для определения силы
Перегруппируем:n
Wm n i
Wm n r
ii
f e k dxk
dxk i ir i dii
x
x
i 1
r 1
i 1
k
k
i
i
Поскольку сила (fe)k не зависит от ii и Ψi, коэффициент dii должен равняться нулю:
Wm n r
i ir i 0
r 1
i 1
i
i
n
Тогда получим уравнение для силы электромеханической связи:
f e k
Wm 1 ,
, n , x1 ,
xk
, xm
n
i
i 1
ii 1 ,
, n , x1 ,
xk
, xm
11. Уравнения электромагнитного момента электрических машин
Для двигателя постоянного тока:M pп L12iв iя
Для асинхронного двигателя:
M pn ( 1d i1q 1q i1d )
M pn Lm (i1q i2 d i1d i2 q )
Lm
(i1q 2 d i1d 2 q )
L2
Lm
M pn
( 1q 2 d 1d 2 q )
2
L1 L2 - Lm
M pn
Для синхронного двигателя:
M pп i1q L1d i1d L12i2 d i1d L1q i1q
12. Модели электромеханических систем с сосредоточенными параметрами
13. Примеры описания обобщенного электромеханического преобразователя
diвu
i
R
L
в
в в в
dt
На базе АД
u i R L diя
я
эл 2
я я я
dt
M pп L12iв iя
d 1 1
dt J ( M М 12 )
1
d 2 1
М 12
J2
dt
dM 12
C12 ( 1 2 )
dt
d 1 / dt u1 - R1 L2 1 - Lm 2
- R1ДПТ
L2 1 - Lm 2
d 1 / dt uНа
1 базе
d 2 / dt - R2 L1 2 - Lm 1 - p 2
d 2 / dt - R2 L1 2 - Lm 1 p 2
i1 L2 1 - Lm 2
i1 L2 1 - Lm 2
i2 L1 2 - Lm 1
i2 L1 2 - Lm 1
1 / ( L1 L2 - L2m )
M Lm p ( 1 2 - 1 2 )
14. Контрольный срез!
Исходя из уравнений ОЭМ выведите уравнение моментаui Ri ii
2q
L
j 1
i, j
di j
dt
2q
эл
j 1
dLi , j
d эл
ij
1 i1 L1 ,1 i1 L1 ,1 i2 d L1a ,2 d i2 q L1 ,2 q
1 i1 L1 ,1 i1 L1 ,1 i2 d L1 ,2 d i2 q L1 ,2 q
2 d i1 L2 d ,1 i1 L2 d ,1 i2 d L2 d ,2 d i2 q L2 d ,2 q
2 q i1 L2 q ,1 i1 L2 q ,1 i2 d L2 q ,2 d i2 q L2 q ,2 q
1 2 q i
M ii
2 i 1 эл
L1 ,2 d L2 d ,1 L12 cos эл
L1 ,2 q L2 q ,1 L12 cos( эл 90 ) L12 sin эл
L1 ,2 d L2 d ,1 L12 sin эл
L1 ,2 q L2 q ,1 L12 cos эл












 physics
physics








