Движение заряженных частиц в магнитных и электрических полях. Электромагнитная индукция, энергия магнитного поля

1. Занятие 5. Движение заряженных частиц в магнитных и электрических полях. Электромагнитная индукция, энергия магнитного поля

МГТУ им.
Н.Э. Баумана
∙ Отклонение от прямолинейной траектории движущейся
заряженной нерелятивистской частицы однородными
электрическим или магнитным полем
∙ Закон Фарадея. Правило Ленца
∙ Индуктивность контура с током. Электродвижущая сила
самоиндукции. Взаимная индуктивность и теорема
взаимности связанных контуров с током
∙ Энергия магнитного поля проводника с током. Плотность
энергии и энергия магнитного поля
∙ Магнитное давление
∙ Ауд.: Иродов И.Е. Задачи по общей физике.
- М.: Бином, 1998 2010. №№ 2.417, 2.433, 2.325, 2.329, 2.374

2. Отклонение от прямолинейной траектории движущейся заряженной нерелятивистской частицы однородными электрическим или магнитным

полем
Э На нерелятивистскую частицу с q зарядом и m
q
q
O
массой, движущуюся с вектором v0 скорости в
v
v
Y
a
v
F E
z вакууме во внешнем однородном электрическом
v
l
l
поле с вектором E напряжённости действует вектор
Z
Fe силы:
Fe = qE, (1)
Рис.1
где q = -|q-| и q = q+ - движущийся с вектором a ускорения по
направлению OZ оси неподвижной OYZ системы координат qотрицательный или q+ положительный заряд. Cмещение z на Э
l1 l1
q
экране q заряда:
z
E 2 ( l 2 ), (2)
m v
2
МГТУ им.
Н.Э. Баумана
-
-
0
0
\\
e
1
2
0
где v0 - модуль вектора v0 начальной скорости
движения q заряда по направлению OY оси.

3.

На нерелятивистскую частицу с q зарядом
Э
q
Y и m массой, движущуюся с вектором v скорости
O
v
0
F
v
a
z
R
в вакууме в магнитном поле с вектором B его
l
l
индукции, действует вектор Fm силы Лоренца:
Z
Рис.2
(3)
Fm = q[v0,B],
где q = -|q-| и q = q+ - движущийся с вектором an нормального
ускорения по направлению OZ оси и окружности R радиусом
неподвижной OYZ системы координат q- отрицательный или q+
положительный заряд. Cмещение z на Э экране q заряда:
l1 l1
q
z
E
( l 2 ), (4)
-
0
m
МГТУ им.
Н.Э. Баумана
× B
q-
n
1
0
2
m
v0
2
где v0 - модуль вектора v0 начальной скорости
движения q заряда по направлению OY оси.

4. Закон Фарадея. Правило Ленца

МГТУ им.
Н.Э. Баумана
Вектор EB напряжённости вихревого электрического
l
·
поля:
EB = [v, B],
p
(5)
v
B×
где
v
=
v
;
v
=
v
векторы
скорости
соответственно
+
Ε
E dS
положительных и отрицательных зарядов,
I
двигающихся во внешнем магнитном поле с B вектором
1
Риc.3
vdt
индукции. Согласно закону Фарадея ЭДС индукции
Εi12 между 1-2 участками перемычки, движущейся с v вектором
(6)
скорости:
Εi12 = - dФm/dt,
где поток Фm магнитной индукции через элементарную поверхность
dS площадью за dt интервал времени изменяется на dФm
величину. ЭДС индукции Εi12 вызывает в проводящем
контуре появление индукционного тока Ii силой с
вектором pmi магнитного момента.
2
Ii
mi
i12
B
i

5.

Z
pmi
Ii
B
B
S
O
Ii
B
B
S
O
Y
X
X
B
dФm/dt > 0; Εi < 0
МГТУ им.
Н.Э. Баумана
Z
Риc.4
B
pmi
dФm/dt < 0; Εi > 0
Y
Согласно правилу Ленца при
постоянной или увеличивающейся
во t времени поверхности S площадью,
охватываемой проводящим контуром,
вектор pmi магнитного момента индукционного тока Ii силой
противонаправлен вектору B индукции внешнего магнитного поля,
если Фm поток индукции внешнего магнитного поля, пересекающего
эту S площадь, увеличивается во времени, т.е. при dФm/dt > 0 ЭДС
индукции Εi < 0. Если dФm/dt < 0, то ЭДС индукции
Εi > 0 , т.е. вектор pmi магнитного момента
индукционного тока Ii силой сонаправлен вектору B
индукции внешнего магнитного поля.

6. Индуктивность контура с током. Электродвижущая сила самоиндукции. Взаимная индуктивность и теорема взаимности связанных

контуров с током
МГТУ им.
Н.Э. Баумана
Потокосцеплением Ψ контура, состоящего из N витков с током Ii
силой в каждом витке, называют сумму потоков Фmi индукции N
внешнего магнитного поля через каждый из этих N витков: Фmi . (7)
i 1
Потокосцепление Ψ проводящего контура пропорционально току I
силой в нём :
Ψ = LI,
(8)
где L - индуктивность контура. Согласно правилу Ленца при
изменениях тока I силой контура в нём возникает ЭДС
самоиндукции Εс, направленная противоположно току I
силой, если он увеличивается во времени t, и по току I
силой, если он уменьшается во времени t : Εс = - LdI/dt.(9)

7.

МГТУ им.
Н.Э. Баумана
ø2R2
Z
B1
B2
2
O
B2
I
I
X
ø2R1
1
Y
Магнитное поле 1 - го контура R1 радиусом
создаёт потокосцепление Ψ21 с поверхностью
2 - го контура R2 радиусом, пропорциональное
току I силой в 1-ом контуре: Ψ21 = L21I,
(10)
где L21 - коэффициент взаимной индуктивности
1 - го контура со 2 - ым.
Риc.5
Магнитное поле 2 - го контура R2 радиусом создаёт потокосцепление
Ψ12 с поверхностью 1 - го контура R1 радиусом , пропорциональное
току I силой во 2 - ом контуре:
Ψ12 = L12I,(11)
где L12 – коэффициент взаимной индуктивности 2 - го
контура с 1 - ым контуром. Согласно теореме взаимности
при отсутствии в среде между проводящими контурами
ферромагнитных материалов: L21 = L12.
(12)

8. Энергия магнитного поля проводника с током. Плотность энергии и энергия магнитного поля

L
t1
I
B
R
Кл Εэ
_
+
t2t2 L
+
Εс
I
Кл Εэ R
_
+
_
I
МГТУ им.
Н.Э. Баумана
Работа A, выполненная ЭДС самоиндукции Εс от
значения тока I силой в момент t2 времени отключения
Рис.6
Εэ внешней ЭДС до времени t → ∞, т.е. I∞ = 0:
A L
I 0
I
LI 2
IdI
2
(13)
Работа A выполнена магнитным полем проводника L индуктивностью
(14)
с током I силой, поэтому его Wm энергия:
Wm = LI2/2.
Плотность wm энергии магнитного поля, выраженная через модули H,
B векторов H напряжённости B индукции магнитного поля с учётом H
= B/μ0μ в среде с μ магнитной проницаемостью:
wm = HB/2 = B2/2μ0μ. (15)
кроме
Энергия Wm магнитного поля среды V объёмом
HB
ферромагнетиков :
Wm wm dV dV .
(16)
V
V
2

9. Магнитное давление

wm1
B1
A-A
A
B1 dr
F1
S r
wm2
×
dV
B2
× ×
×
×
×
B2
×
×
I
A
Рис.7
F2
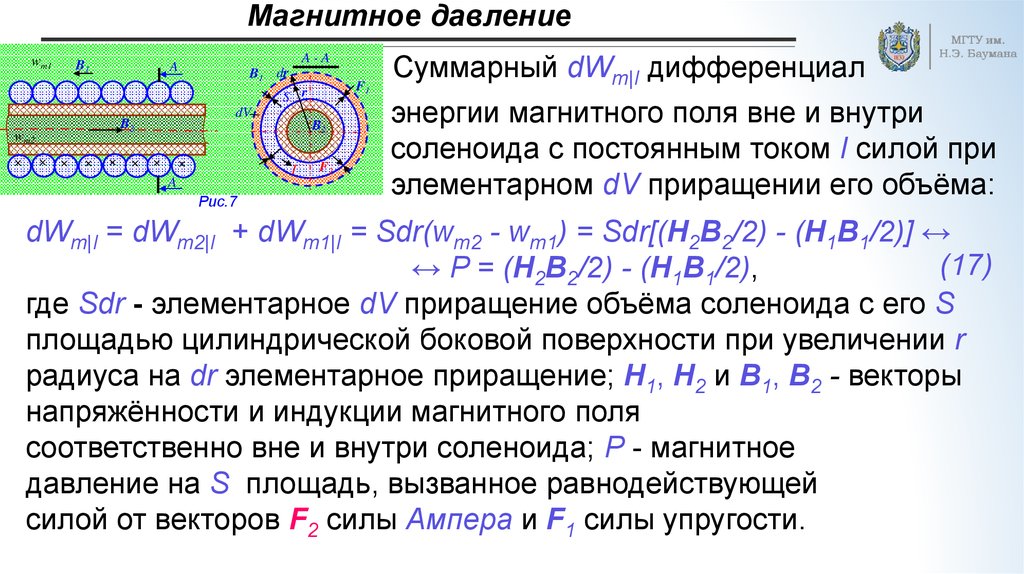
Суммарный dWm|I дифференциал
МГТУ им.
Н.Э. Баумана
энергии магнитного поля вне и внутри
соленоида с постоянным током I силой при
элементарном dV приращении его объёма:
dWm|I = dWm2|I + dWm1|I = Sdr(wm2 - wm1) = Sdr[(H2B2/2) - (H1B1/2)] ↔
(17)
↔ P = (H2B2/2) - (H1B1/2),
где Sdr - элементарное dV приращение объёма соленоида с его S
площадью цилиндрической боковой поверхности при увеличении r
радиуса на dr элементарное приращение; H1, H2 и B1, B2 - векторы
напряжённости и индукции магнитного поля
соответственно вне и внутри соленоида; P - магнитное
давление на S площадь, вызванное равнодействующей
силой от векторов F2 силы Ампера и F1 силы упругости.

10. Задача №2.417

Нерелятивистская заряженная частица пролетает
МГТУ им.
Н.Э. Баумана
электрическое поле цилиндрического конденсатора и затем попадает
в однородное поперечное магнитное поле с индукцией B. В
конденсаторе частица движется по дуге окружности, в магнитном
поле – по полуокружности радиуса r. Разность потенциалов на
конденсаторе U, радиусы обкладок a и b, причём a < b. Найти
скорость частицы и её удельный заряд q/m. Дано: B, a < b, U/v = ?
q/m = ?l Ответ: v = U/rBln(b/a), q/m = U/r2B2ln(b/a).
Решение
+
U
-
b
a
R
v
+ q, m
+ F
e
B
v
Fm
r
+
Рис.8
v
Согласно теореме Гаусса Dr проекция
вектора Dr электрического смещения на
направление r радиуса – вектора для
цилиндрического поля D вектора между
обкладками конденсатора:

11.

Dr2πRl = UC ↔ Dr2πrl = U2πε0εl/ln(b/a) ↔ Dr = Uε0ε/rln(b/a),(18)
где S = 2πRl – площадь боковой поверхности воображаемого
цилиндра, часть которого пролетает нерелятивистская заряженная
частица по окружности R радиусом; C = 2πε0εl/ln(b/a) - емкость
цилиндрического конденсатора с l длиной обкладок, к которым
приложено постоянное U напряжение. В однородном изотропном
диэлектрике D = εε0E, поэтому: Er = Uε0ε/ε0ε Rln(b/a) = U/Rln(b/a). (19)
Модуль Fe вектора Fe электрической силы, являющийся модулем Fцс
центростремительной силы при движении нерелятивистской частицы
c q зарядом, m массой по окружности R радиусом: Fe = Fцс↔
↔ qEr = mv2/r ↔ qU/rln(b/a) = mv2/r ↔ v 2 q U , (20)
МГТУ им.
Н.Э. Баумана
m ln b
a
где v – линейная скорость вращения этой частицы.
После попадания частицы q зарядом, m массой в
однородное магнитное поле, модуль которого равен B,

12.

а вектор направлен перпендикулярно v вектору скорости,
на эту частицу со стороны магнитного поля действует
вектор Fm силы Лоренца, являющийся центростремительной силой
при движении нерелятивистской частицы c q зарядом, m массой по
окружности r радиусом:
Fm = Fцс↔ Bvq = mv2/r ↔ v = (q/m)Br. (21)
Из двух уравнений, в которых неизвестны q/m удельный заряд
нерелятивистской частицы q зарядом, m массой и её v скорость:
МГТУ им.
Н.Э. Баумана
q
U
U
2 2
;v
. (22)
m B r ln b
Br ln b
a
a

13. Задача №2.433

В бетатроне магнитный поток внутри равновесной орбиты радиуса
r = 25 см возрастает за время ускорения практически с постоянной
скоростью dФ/dt = 5,0 Вб/с. При этом электроны приобретают
энергию W = 25 Мэв. Найти число оборотов, совершенных
электроном за время ускорения, и соответствующее значение
пройденного пути.
Ответ: NZ = W/eФ = 5∙106 оборотов, s = 2πrN = 8∙103 км .
r
F
Решение. Дано: r, dФ/dt, W / N = ? s =?
E
S
v
j
Согласно закону Фарадея ЭДС индукции Εi в
p
O
F
F
Y проводящем контуре, образованном
v
X B
j
F
движущимися электронами, на
Рис.9
который "натянута" поверхность
S площадью при наличии изменяющегося со скоростью
dФm/dt во t времени внешнего Фm магнитного потока,
e
B
i
mi
m
EB
МГТУ им.
Н.Э. Баумана
i
m
e

14.

пронизывающего эту поверхность:
Εi= - dФm/dt.
(23)
МГТУ им.
Н.Э. Баумана
ЭДС индукции Εi определяется циркуляцией вектора EB
напряжённости вихревого электрического поля по окружности 2πr
длиной, по которой движутся электроны, вследствие наличия
вектора Fm силы Лоренца, являющейся центростремительной силой:
Εi = ∫ EBdl.
(24)
2πr
Модуль EB вектора EB напряжённости вихревого электрического
(25)
поля из (23), (24):
EB2πr = dФm/dt ↔ EB = (dФm/dt)/2πr.
Модуль Fe вектора Fe силы, действующего на e электрон, вследствие
наличия вихревого электрического поля с
модулем EB вектора EB его напряжённости:
Fe = eEB = e(dФm/dt)/2πr. (26)
Согласно уравнению изменения механической

15.

энергии приращение ΔWk кинетической энергии e электрона
МГТУ им.
Н.Э. Баумана
равно работе Aст сторонней силы, которая равна работе вектора Fe
силы на длине 2πrN пути при ускоренном вращении e электрона с N
количеством оборотов по окружности 2πr длиной: ΔWk = Fe 2πrN ↔
↔ ΔWk = e(dФm/dt)2πrN/2πr ↔ N = ΔWk/e(dФm/dt) =
= 25∙106∙1,6∙10-19/ 1,6∙10-19 ∙5,0 [Дж∙с/Кл∙Вб] =
(27)
= 5 ∙106 [кг ∙м2 ∙с ∙ с2 ∙А /с2 ∙А ∙с ∙м2 ∙ кг] = 5 ∙106 об.
Пройденный s путь при ускоренном вращении e электрона с N
количеством оборотов по окружности 2πr длиной:
(28)
s = 2πrN = 6,28 ∙0,25 ∙ 5 ∙106 [м] ≈ 8 ∙103 км.

16. Задача №2.325

МГТУ им.
Н.Э. Баумана
На расстоянии a и b от длинного прямого проводника с постоянным
током I0 расположены два параллельных ему провода, замкнутых
на одном конце сопротивлением R. По проводам без трения
перемещают с постоянной скоростью v стержень-перемычку.
Пренебрегая сопротивлением проводов и стержня, а также
магнитным полем индукционного тока, найти: а) индукционный ток
в стержне; б) силу, нужную для поддержания постоянства скорости.
Ответ: а) Ii = (μ0I0 v/2πR)ln(b/a); б) F = (μ0I0/2π)2ln2(b/a)∙v/R.
2
Z
B
Ii
pmi ·
FA
R
z
dl
dFA
dS S
1
O
+
I0
y
Рис.10
v
F Ei12
b
dz
a
Y
Решение. Дано: a, b, R, I0 / Ii = ? FА =?
Согласно правилу Ленца при
увеличивающейся во t времени
поверхности S площадью,
охватываемой проводящим контуром,

17.

вектор pmi магнитного момента индукционного тока Ii силой
противонаправлен вектору B индукции внешнего магнитного
поля, если Фm поток индукции этого поля, пересекающего S
площадь, увеличивается во времени, т.е. при dФm/dt > 0 ЭДС
индукции Εi < 0. Поэтому на рис. 10 вектор pmi магнитного момента
противонаправлен вектору B индукции внешнего магнитного поля,
индукционный ток Ii силой по правилу "буравчика" направлен
против "часовой стрелки", а ЭДС индукции Εi направлена в
проводящем контуре от нижнего к верхнему проводнику. Модуль B
вектора B магнитной индукции поля, пересекающего в вакууме
охватываемой проводящим контуром поверхность S
площадью и находящегося на z расстоянии от длинного
прямого проводника c током I0 силой:B = μ0I0/2πz. (29)
Поток dФm магнитной индукции через элементарную
поверхность dS площадью y длиной и dz шириной:
МГТУ им.
Н.Э. Баумана

18.

dФm = Bydz ↔ dФm = μ0I0ydz/2πz.
(30)
Поток Фm магнитной индукции через поверхность S площадью,
охватываемой проводящим контуром
y длинойb и b - a шириной:
b
0 I 0 ydz 0 I 0 y b
Фm dФm Фm
ln .
a
2 z
2
a
a
МГТУ им.
Н.Э. Баумана
(31)
Согласно закону Фарадея ЭДС индукции Εi12 между 1-2 участками
стержня-перемычки, движущейся с v вектором скорости:
dФm
0 I 0 dy b
0 I 0v b
(32)
Ei12
ln
ln ,
dt
2 dt
a
2
где v = dy/dt – постоянная скорость перемещения стержня
- перемычки по OY оси. Индукционный ток Ii силой в нём:
E i12
0 I 0v
Ii
ln b , (33)
a
R
2 R
где R – сопротивление резистора, замыкающего два
параллельных провода на левом конце контура.
Модуль dFА элементарного вектора dFА силы Ампера,
a

19.

действующего на проводник с током Ii силой и малой dl
шириной, направлен перпендикулярно к плоскости,
образованной векторами dl и B индукции внешнего магнитного поля,
так, что из конца этого элементарного вектора dFА силы Ампера
вращение по кратчайшему расстоянию от направления вектора dl к
направлению вектора B индукции внешнего магнитного поля видно
происходящим против "часовой
стрелки":
( 0 I 0 ) 2 v b dz
dFA I i dl B dFA I i Bdz
ln
.(34)
2
a z
(2 ) R
Модуль FА вектора FА силы Ампера, действующего на проводник с
током Ii силой и b - a шириной:
МГТУ им.
Н.Э. Баумана
( 0 I 0 ) 2 v b dz
( 0 I 0 ) 2 v
b ) 2 .(35)
FА dFA FА
ln
(ln
2
2
a z
a
(
2
)
R
(
2
)
R
a
a
b
b
Вектор F уравновешивающей силы для постоянной
скорости v движения стержня-перемычки, равен по
модулю и противоположен по направлению вектору
FА силы Ампера.

20. Задача №2.329

Плоская спираль с большим числом витков N, плотно прилегающих
друг к другу, находится в однородном магнитном поле,
перпендикулярном плоскости спирали. Наружный радиус витков
спирали равен a. Индукция поля изменяется во времени по закону
B = B0 sinωt, где B0 и ω – постоянные. Найти амплитудное значение
ЭДС индукции в спирали.
2NωB /3. Решение. Дано:N, a, B = B sinωt / E = ?
Ответ:
E
=
πa
im
0
0
im
r
a
N Радиус rn n-го витка a/N шириной с учётом их плотного
(36)
прилегания
друг
к
другу:
r
=
(a/N)n,
n
a/N
E
где n = 1,2,…,N – номер витка.
n
B
МГТУ им.
Н.Э. Баумана
i
Рис.11
Площадь Sn круга с rn радиусом:Sn = πrn2 = π(an/N)2. (37)
Поток Фmn магнитной индукции через площадь Sn
круга, охватываемой n-ым витком спирали:

21.

(38)
Фmn = B0π(an/N)2sinωt.
Согласно закону Фарадея амплитуда Ε0n ЭДС индукции,
возникающей в n-ом витке спирали:
(39)
Εn = - dФm/dt = - B0π(an/N)2ωcosωt ↔ Ε0n = B0π(an/N)2ω.
Результирующая Ε0Σ амплитуда ЭДС индукции, возникающая на
выводах спирали, от сложения всех амплитуд в её N витках:
a 2 2
E 0 E 01 E 02 ... E 0 n ... E 0 N B0 2 (1 2 2 ... n 2 ... N 2 )
N
a 2 N ( N 1)( 2 N 1)
a 2 N
E 0 B0 2
B0
,
6
3
N
где
N ( N 1)( 2 N 1) N 3
(1 2 ... n ... N )
6
3
2
2
2
2
- сумма конечного числового ряда при N >> 1.
(41)
(40)

22. Задача №2.374

МГТУ им.
Н.Э. Баумана
Два соленоида одинаковой длины и почти одинакового сечения
вставлены один в другой. Найти их взаимную индуктивность, если
их индуктивности равны L1 и L2.
Ответ: L12 L1 L2 .
Решение.
Дано: L1, L2/ L12 = ? L21 = ?
Внутренний и внешний соленоиды имеют
l, N
I
одинаковый V = lS объём, количество n1, n2
I
B
· ·· ····· ·· ·· n
витков на единицу их равной l длины, заполнен
· · · · · · · ·
p
μ
B
S
магнетиком с μ магнитной
I
× × × × × × × ×
проницаемостью,
поэтому
обладают
× × × × × × × × × ×× × ×
I
l, N n
L1, L2 индуктивностями:
2V; L = μ μn 2V. (42)
dB /dt < 0
L
=
μ
μn
1
0
1
2
0
2
Рис.12
1
2
1
1
1
m2
1
1
2
2
2
1
Модуль B1 вектора B1 индукции магнитного поля,

23.

перпендикулярного поверхности S площадью поперечного сечения
внутреннего соленоида c током I1 силой:
B1 = μμ0n1I1.
(43)
Равные потоки Ф1 = Ф2 магнитной индукции через поверхность S
площадью поперечного сечения внутреннего и внешнего
соленоидов:
Ф1 = Ф2 = B1S = μμ0n1I1S. (44)
Потокосцепление Ψ21 внешнего соленоида:
Ψ21 = Ф2N2 = μμ0n1I1Sn2l,
(45)
где N2 = n2l – количество витков на l длине этого соленоида.
Потокосцепление Ψ21 внешнего соленоида пропорционально току
I1 силой во внутреннем соленоиде: Ψ21 = L21 I1 ↔
↔ μμ0n1I1Sn2l = L21 I1 ↔ L21 = μμ0n1Sn2l ↔
↔ L21 = μμ0n1Sn2l ↔ L21 = n1(μμ0Sl)1/2n2(μμ0Sl)1/2 ↔

24.

↔ L21 = n1(μμ0V)1/2n2(μμ0V)1/2 ↔ L21 = L12 = (L1 L2)1/2,
(46)
где L21 - коэффициент взаимной индуктивности внутреннего
соленоида с внешним, равный согласно теореме взаимности L12
коэффициенту взаимной индуктивности внешнего соленоида с
внутренним.
Дома: Иродов И.Е. Задачи по общей физике.- М.: Бином,
1998 2010. №№ 2.377, 2.375
Спасибо за внимание!