Движение заряженной частицы в электрическом и магнитном полях. Лекция 6

1. Лекция 6. Движение заряженной частицы в электрическом и магнитном полях

1.Сила Лоренца.
2.Движение заряженной частицы в
электрическом и магнитном полях.
3.Ускорение заряженных частиц.
4.Эффект Холла.
1

2.

Чтобы дойти до цели, нужно прежде всего идти.
О. Бальзак

3.

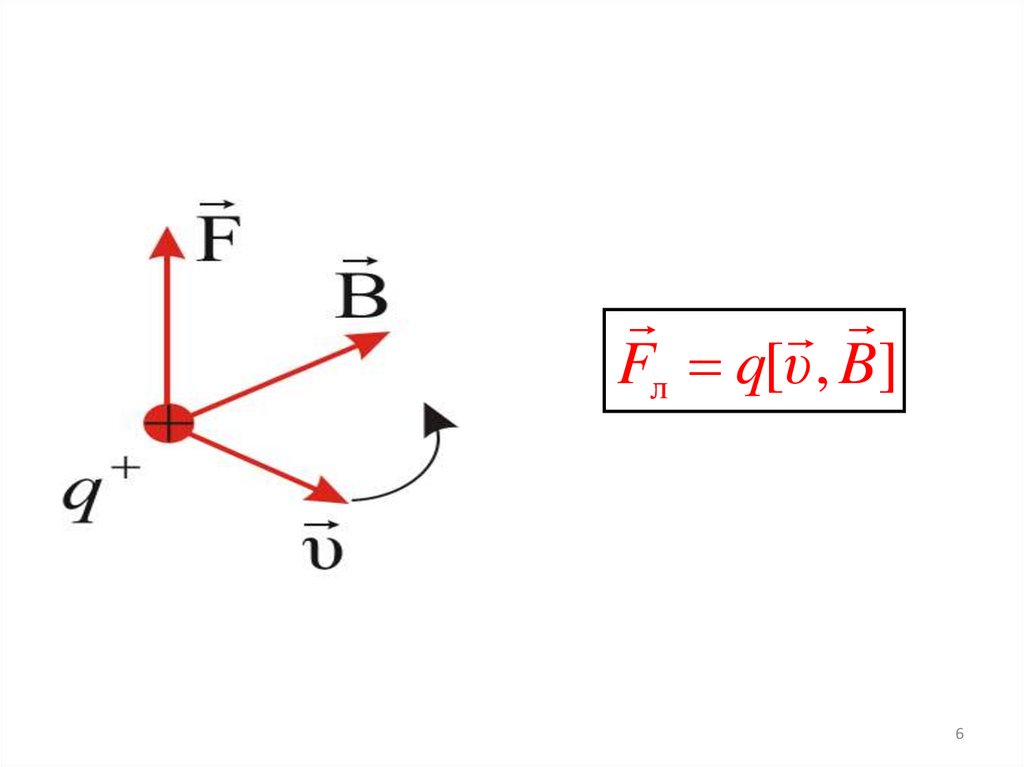
Сила Лоренца
Сила,
действующая
на
движущийся
электрический заряд q во внешнем магнитном
поле.
Fл q[v, B]
Выражение для этой силы было получено в
конце XIX в. голландским физиком
Г.А. Лоренцем
3

4.

Голландский
физик
Г. А. Лоренц
4

5. Вывод формулы для расчета силы Лоренца из силы Ампера

Электрический ток это совокупность большого
числа зарядов n движущихся со скоростью υ
По закону Ампера сила, действующая на проводник
с током в магнитном поле
но ток
I jS ,
dF I [dl , B]
причем j qnv , тогда
dF qvnS dl , B qnSdl v, B
5

6.

Fл q[υ , B]
6

7.

Модуль лоренцевой силы:
Fл qvB sinα
v
иB .
где α – угол между
на заряд, движущийся вдоль линии B (sin α = 0)
сила не действует.
Направлена сила Лоренца перпендикулярно к
плоскости, в которой лежат векторы v и B .
К движущемуся положительному заряду применимо
правило левой руки или «правило буравчика»
7

8.

Правило
левой руки
8

9.

9

10.

10

11. Связь между силой Лоренца и силой Ампера

Fл = Fа /N
FA = F·N
где F – сила Лоренца;
N - число частиц.
Отсюда F = FA /N
I = nqvS
N = nSl
Подставив эти выражения
в формулу для силы Ампера,
получим выражение для силы
Лоренца в магнитном поле:
F = qvBˑsinα.
Fа
Fлоренца
11

12.

• Так как сила Лоренца направлена
перпендикулярно движущемуся заряду, т.е.
перпендикулярно v , работа этой силы
всегда равна нулю.
• Следовательно, действуя на заряженную
частицу, сила Лоренца не может изменить
кинетическую энергию частицы.
12

13.

Постоянное магнитное поле изменяет направление движения
частицы, но не величину скорости.
Магнитная часть силы Лоренца оставляет неизменной
меняет лишь направление импульса, а не энергию
заряда.
Формула Лоренца
позволяет связать уравнения
электромагнитного поля с уравнениями движения
заряженных частиц:
2
m
d r
dt
2
q E q v, B
Здесь действуют оба поля - электрическое Е и магнитное В.
13

14.

• Действие магнитной силы на движущийся заряд можно
наблюдать на экране кинескопа.
• Если поднести постоянный магнит к плоскости экрана,
то легко заметить его воздействие на электронный
пучок по возникающим в изображении искажениям.
14

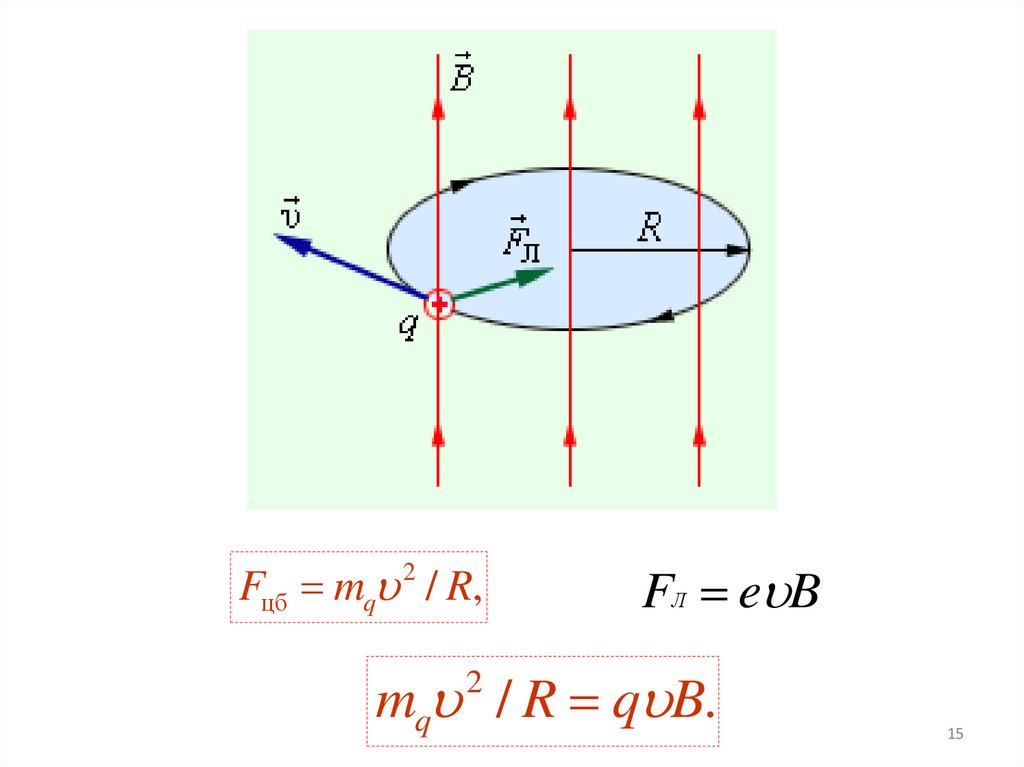
15.

Fцб mq / R,
2
FЛ e B
mq / R q B.
2
15

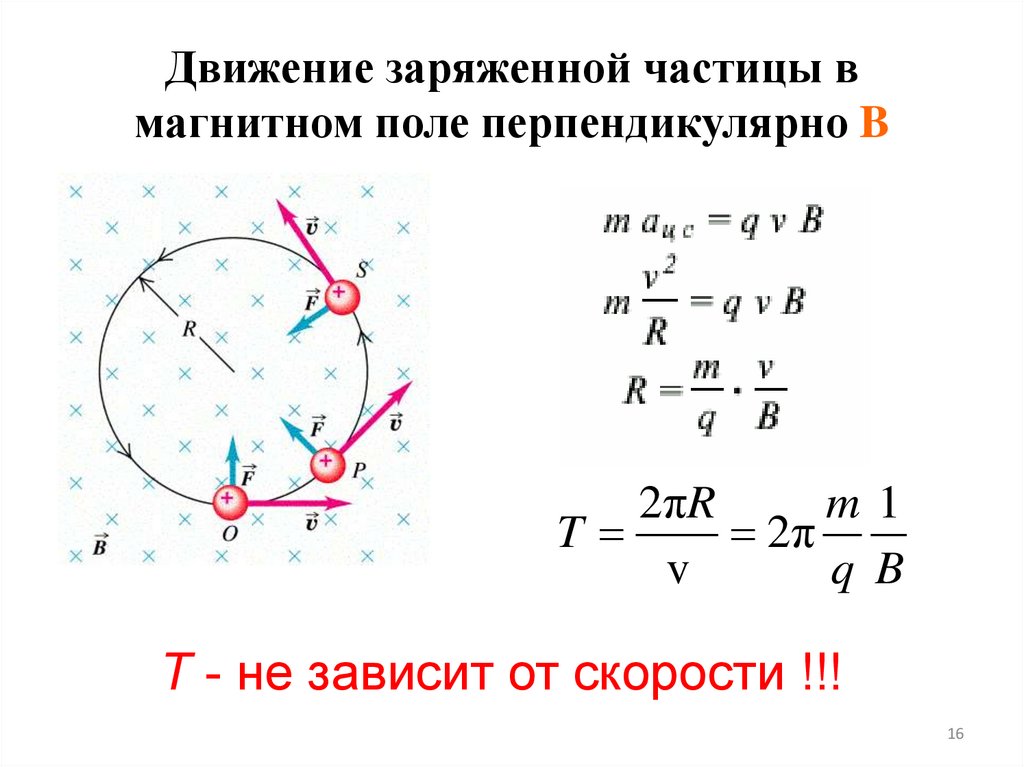
16. Движение заряженной частицы в магнитном поле перпендикулярно B

2πR
m1
T
2π
v
q B
Т - не зависит от скорости !!!
16

17.

Движение заряженной частицы в
магнитном поле под углом к B
Обозначения составляющих скорости даны относительно вектора В
17

18.

Модуль магнитной силы
Шаг винтовой траектории:
18

19.

Силы, действующие на заряженную частицу в
скрещенных электрическом и магнитном поле
Если поле Е направлено под углом β к магнитному полю В, то
представив
E EII E
относительно направления В,
получим три составляющих движения:
q
aII E cos (вдоль вектора В);
- с постоянным ускорением
m
- равномерное вращение qB
(в плоскости В)
m
- дрейф со скоростью v Д E , 2B в направлении, определяемом
B
векторным произведением E , B
19

20.

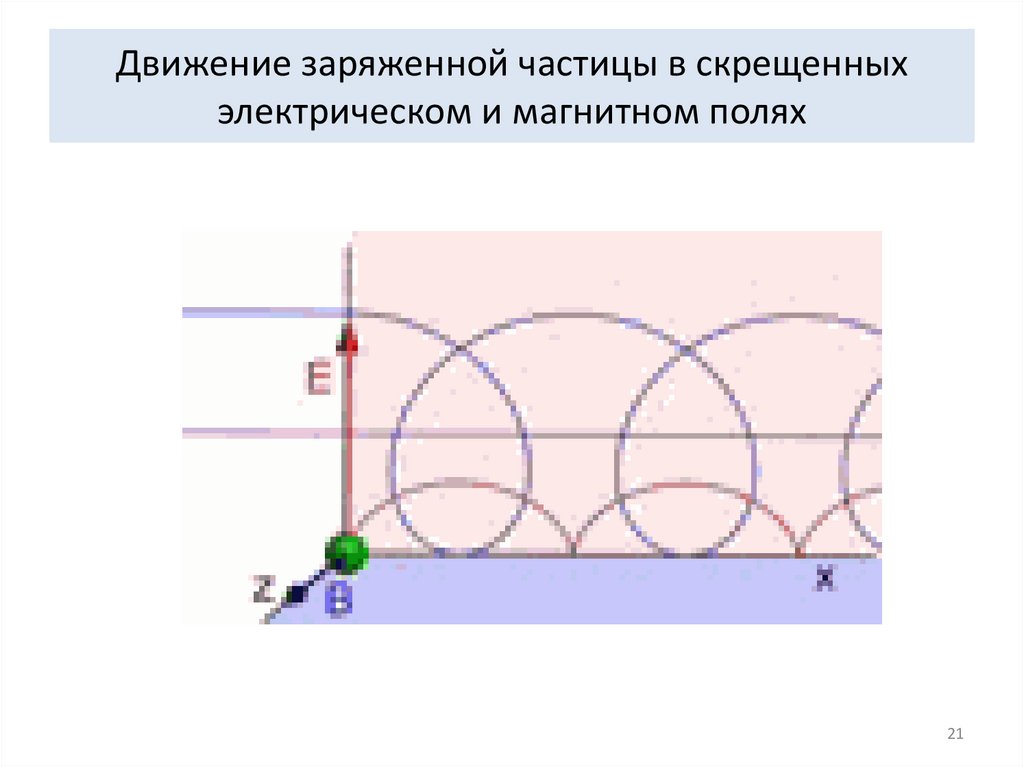
20

21. Движение заряженной частицы в скрещенных электрическом и магнитном полях

21

22.

Траектория движения частицы описывается трохоидой, которую можно
представить как сумму двух движений: в направлении, перпендикулярном
скрещенным полям, заряд движется с постоянной дрейфовой скоростью Vд =
E/В. В плоскости, перпендикулярной магнитному полю, он движется по
окружности с циклотронной частотой ω= qВ/m и радиусом R = |(V0-E/В)/ ω|,
где V0 - начальная скорость заряда.
22

23.

Скорость дрейфа в направлении оси X не зависит от начальной скорости
заряженной частицы. В частности при нулевой начальной скорости
траектория движения будет представлять циклоиду, как показано на рисунке.
Если частица влетает в скрещенное электрическое и магнитное поле со
скоростью, равной скорости дрейфа V = Vд = E/В, то сила действия со
стороны магнитного поля в точности компенсирует силу, действующую со
стороны электрического поля и полная сила Лоренца равна нулю. В этом
случае заряд будет двигаться по прямолинейной траектории со скоростью
дрейфа.
23

24.

Красные частицы положительный заряд, синие - отрицательный
24

25.

Трохоида – (греч. Колесообразный)
25

26.

Удлинённая циклоида r = 1 , h = 1, 5
Укороченная циклоида r = 1; h = 0,8
26

27.

Лабораторная работа Э5
27

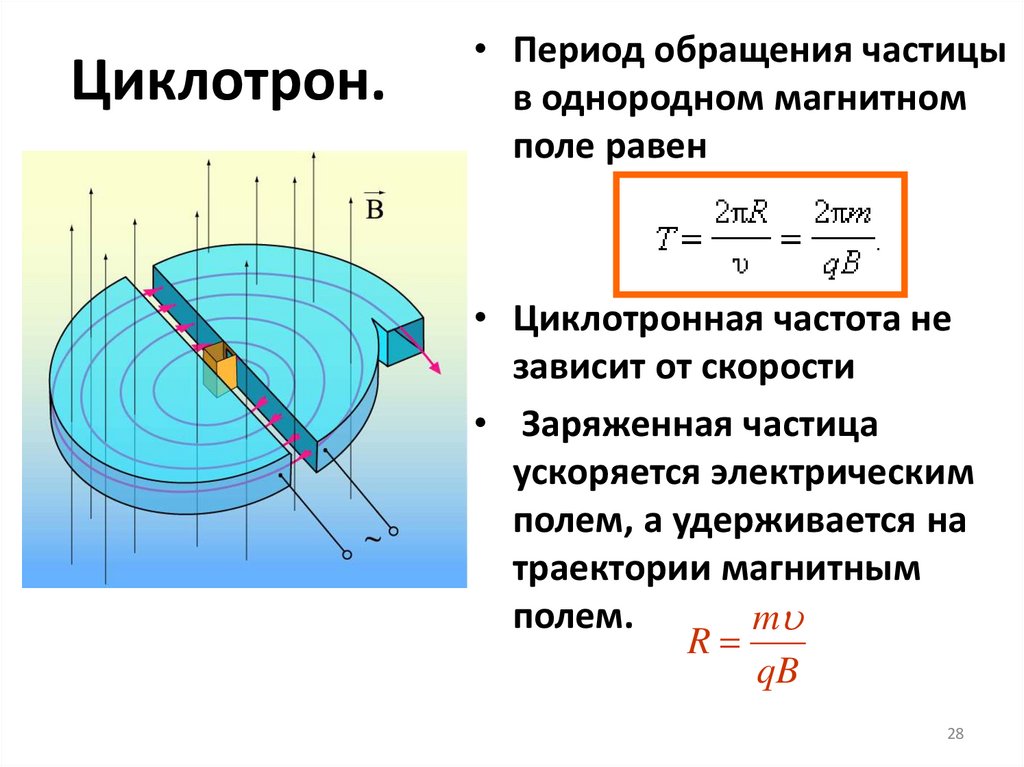
28. Циклотрон.

• Период обращения частицы
в однородном магнитном
поле равен
• Циклотронная частота не
зависит от скорости
• Заряженная частица
ускоряется электрическим
полем, а удерживается на
траектории магнитным
полем.
m
R
qB
28

29.

Фазотрон (синхроциклотрон) – циклический
резонансный ускоритель тяжелых заряженных
частиц (например, протонов, ионов, α-частиц),
• управляющее магнитное поле постоянно,
• частота ускоряющего электрического поля медленно
изменяется с периодом.
Синхротрон – циклический резонансный
ускоритель ультрарелятивистских электронов, в
котором управляющее магнитное поле
изменяется во времени, а частота ускоряющего
электрического поля постоянна.
29

30.

Синхрофазотрон –
изменяют и частоту и
магнитное поле
30

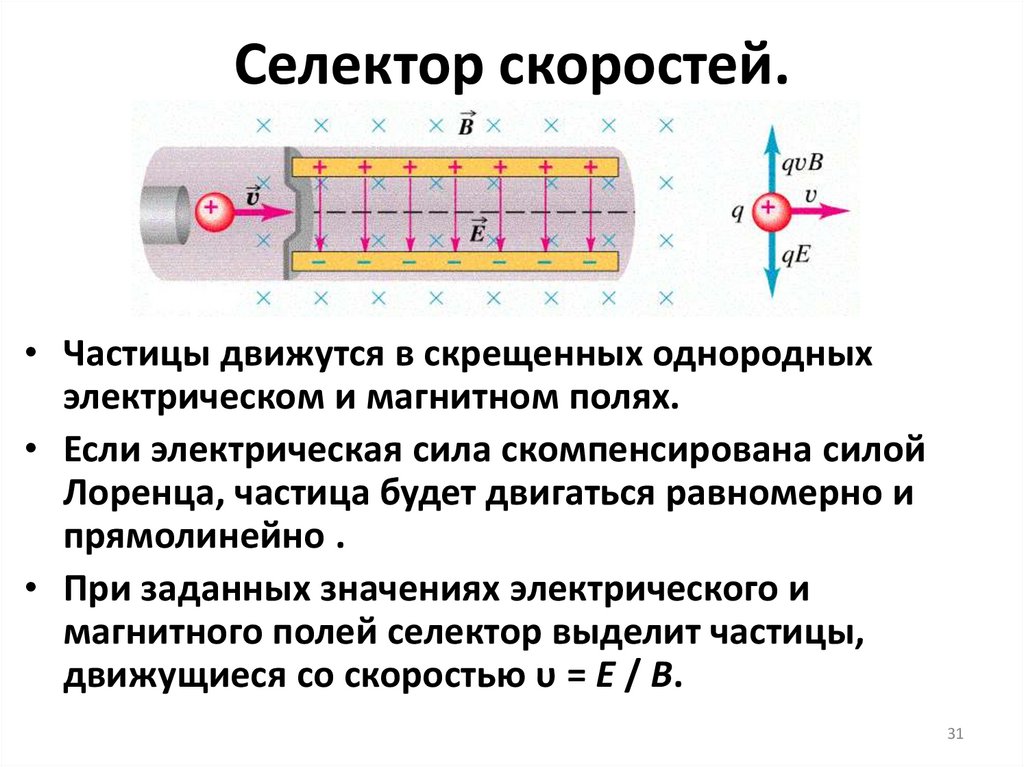
31. Селектор скоростей.

• Частицы движутся в скрещенных однородных
электрическом и магнитном полях.
• Если электрическая сила скомпенсирована силой
Лоренца, частица будет двигаться равномерно и
прямолинейно .
• При заданных значениях электрического и
магнитного полей селектор выделит частицы,
движущиеся со скоростью υ = E / B.
31

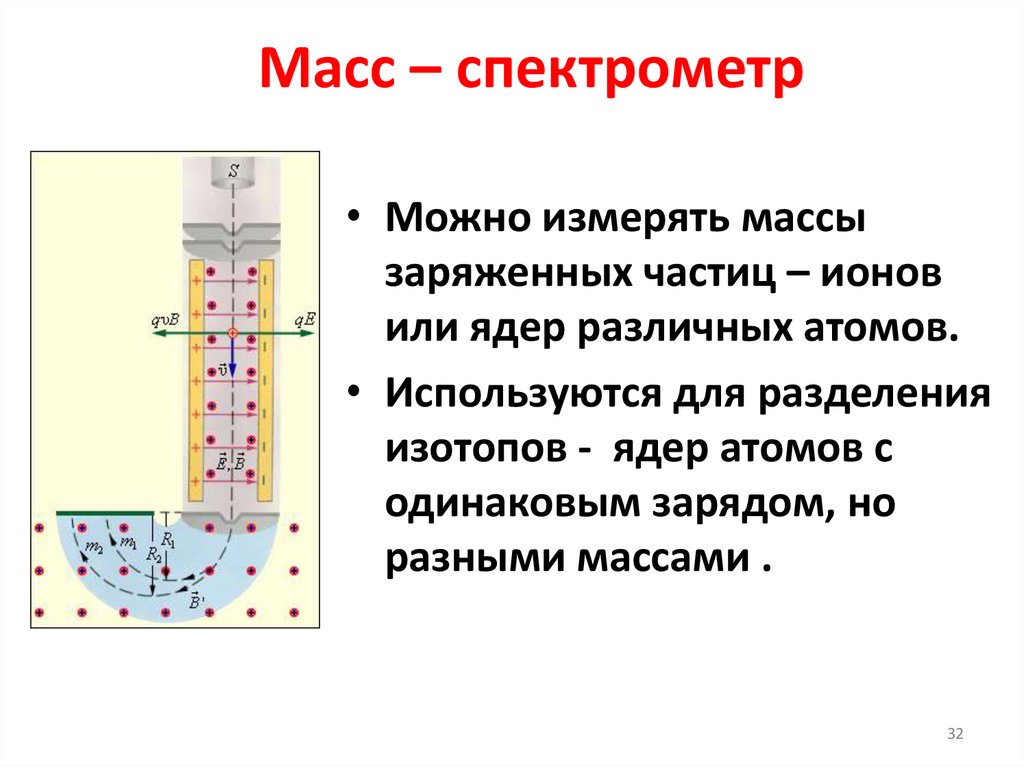
32. Масс – спектрометр

• Можно измерять массы
заряженных частиц – ионов
или ядер различных атомов.
• Используются для разделения
изотопов - ядер атомов с
одинаковым зарядом, но
разными массами .
32

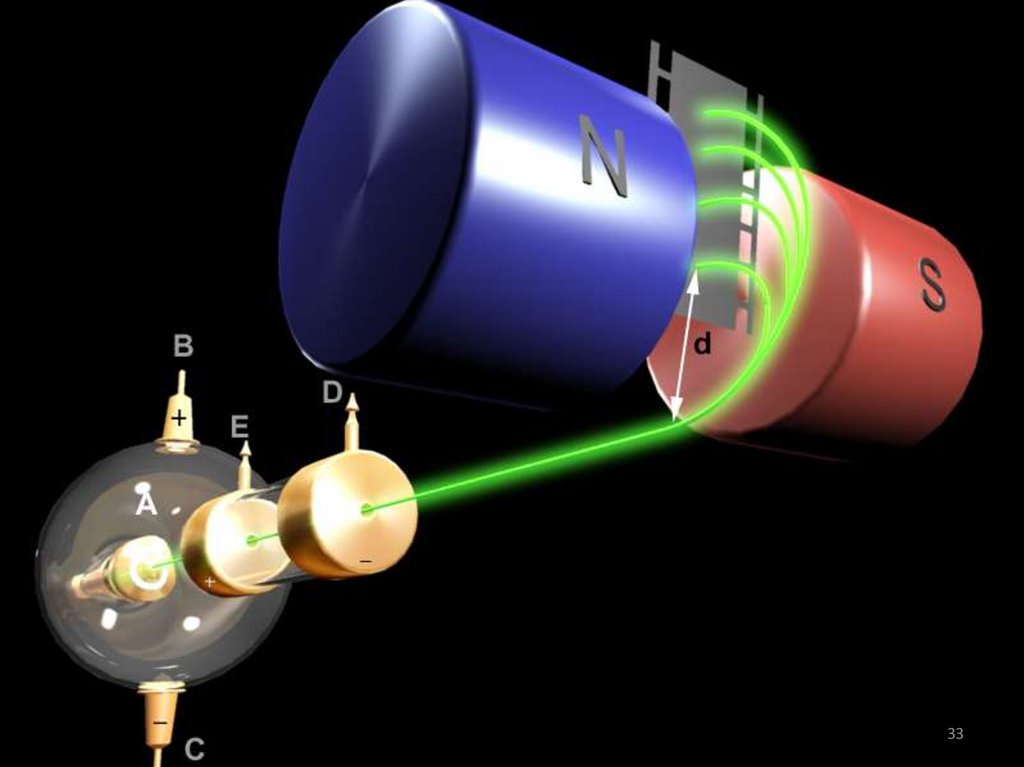
33. Масс – спектрометр.

• Траектории частиц представляют
собой окружности радиусов
R = mυ / qB'.
• Измеряя радиусы траекторий
при известных значениях υ и B'
можно определить отношение
q / m.
• В случае изотопов (q1 = q2) массспектрометр позволяет
разделить частицы с разными
массами.
33

34. Магнитная «бутылка» или ионная ловушка.

• Заряженные частицы не выходят за пределы
«бутылки».
• Используется для удержания плазмы в
управляемом термоядерном синтезе.
34

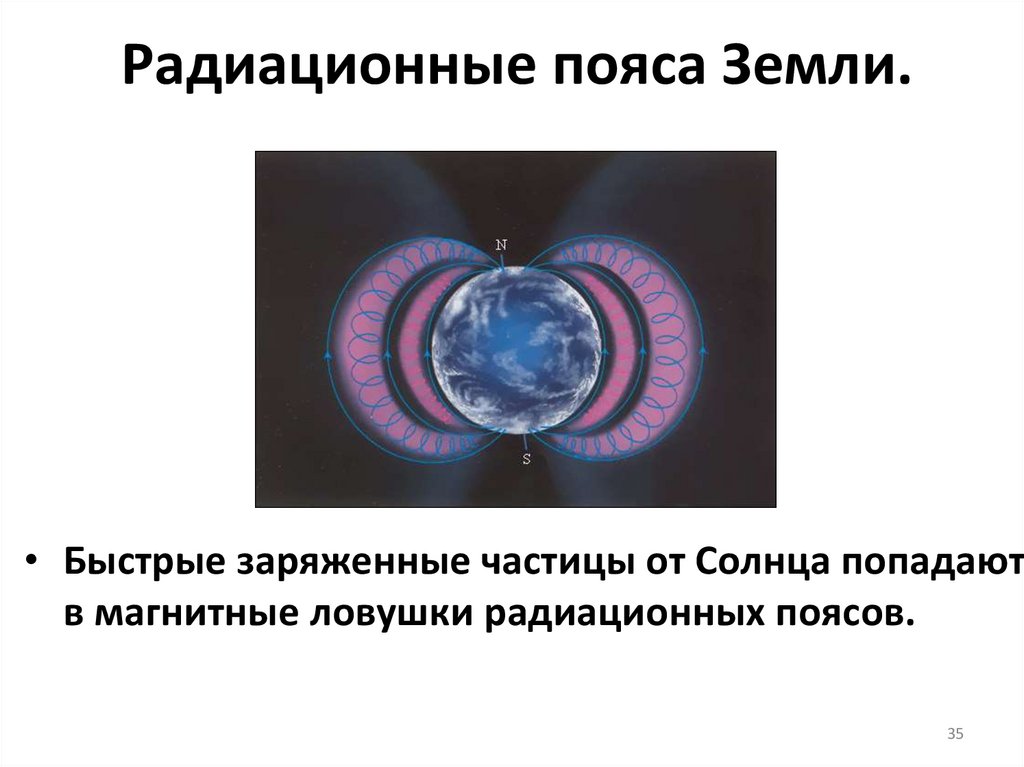
35. Радиационные пояса Земли.

• Быстрые заряженные частицы от Солнца попадают
в магнитные ловушки радиационных поясов.
35

36.

36

37. Эффект Холла

Одним из проявлений магнитной
составляющей силы Лоренца в веществе служит
эффект, обнаруженный в 1879 г. американским
физиком Э.Г. Холлом (1855–1938).
Эффект Холла состоит в возникновении
на боковых гранях проводника с током,
помещенного в поперечное магнитное поле,
разности потенциалов, пропорциональной
величине тока I и индукции магнитного поля
В.
37

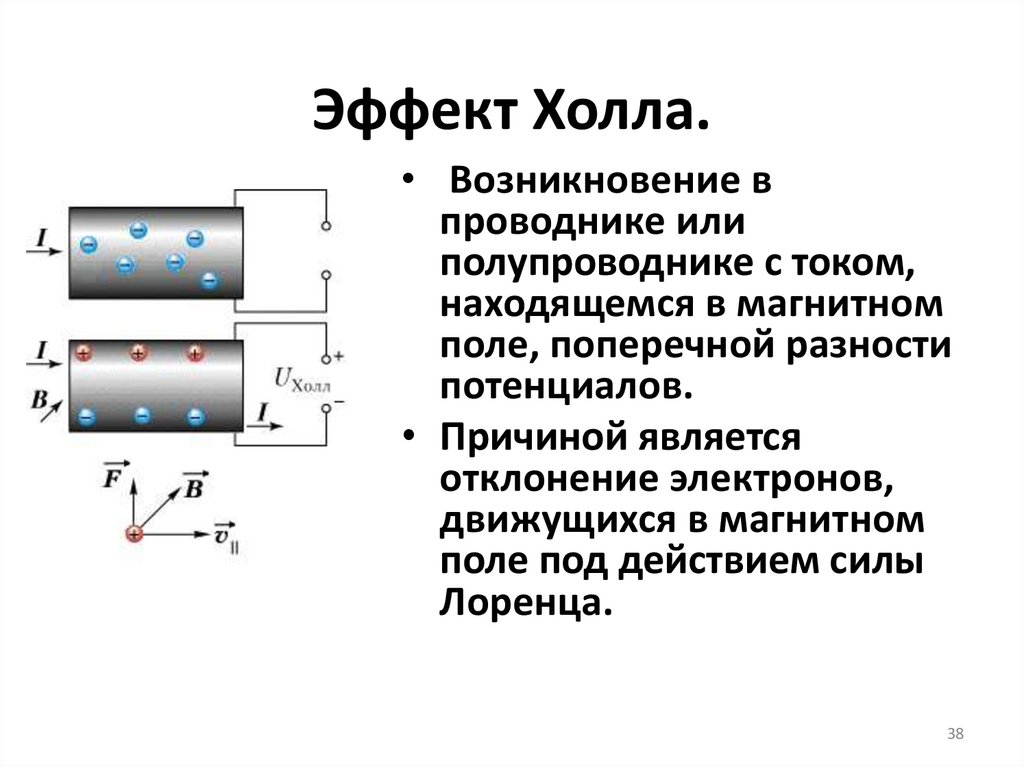
38. Эффект Холла.

• Возникновение в
проводнике или
полупроводнике с током,
находящемся в магнитном
поле, поперечной разности
потенциалов.
• Причиной является
отклонение электронов,
движущихся в магнитном
поле под действием силы
Лоренца.
38

39.

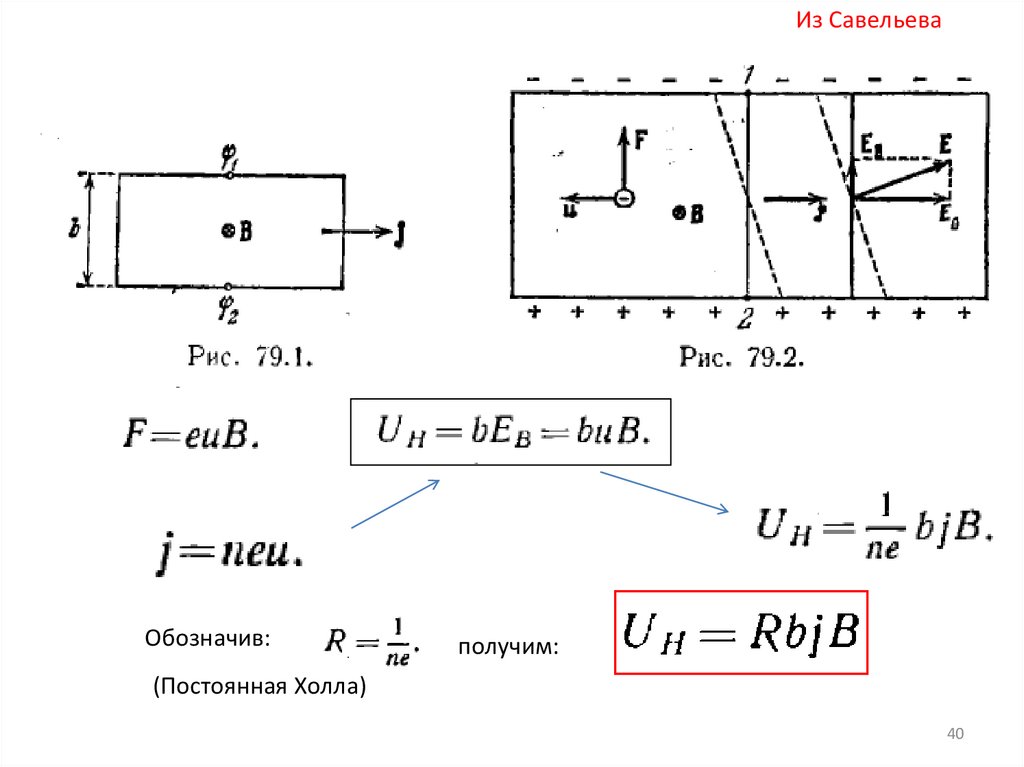
39

40.

Из Савельева
Обозначив:
получим:
(Постоянная Холла)
40

41.

Подвижность носителей тока
скорость
v
П
напряженность E
41

42.

В зависимости от типа носителей тока, на верхней
плоскости будет + или -
42

43. МГД - генератор.

• Работа основана на эффекте Холла.
43

44. Конец лекции 6

Далее тесты, презентация «Ток
поляризации» и демонстрационные
опыты по электромагнетизму
44

45.

45

46.

46

47.

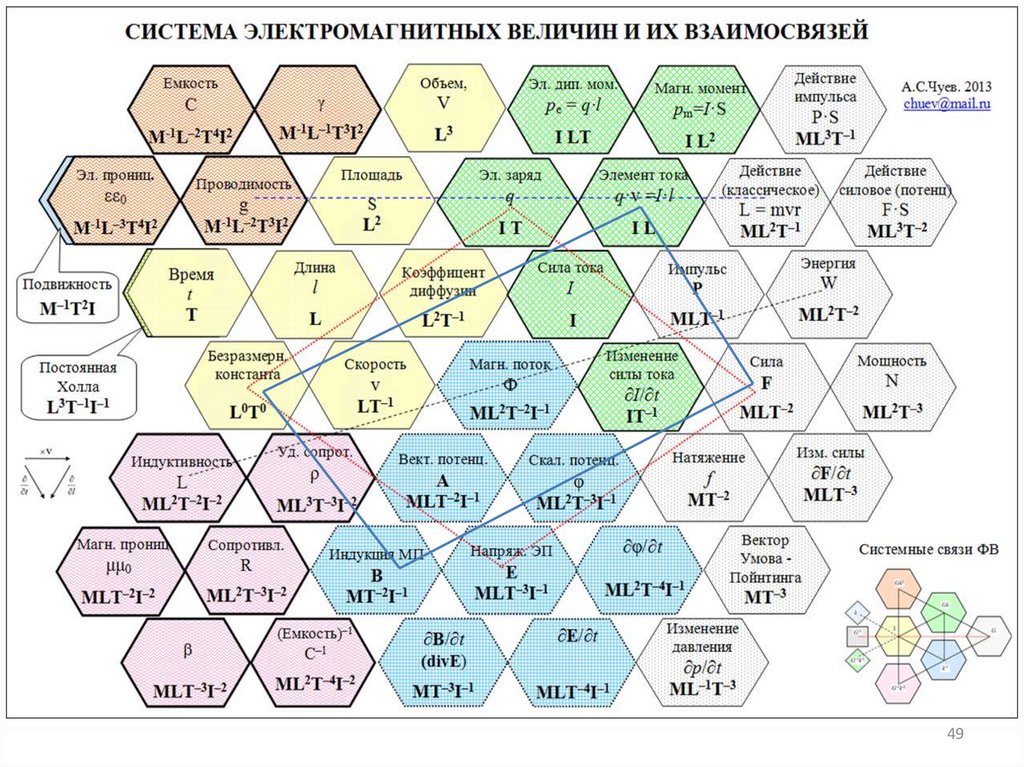
Аналогии электромагнетизма
47

48.

48

49.

49