Similar presentations:
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца
1. «Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца»
2.
Сила ЛоренцаСилу, действующую на движущуюся заряженную
частицу со стороны магнитного поля, называют
силой Лоренца
Хеендрик Антоен Лоеренц (1853 - 1928)
выдающийся голландский физик и математик ,
развил электромагнитную теорию света и
электронную теорию материи, а также
сформулировал теорию электричества,
магнетизма и света, внёс большой вклад в
развитие теории относительности,
лауреат Нобелевской премии 1902г.
3.
FFЛ
N
I qn S
F I B l sin
N nS l
F q n SB l sin q NB sin
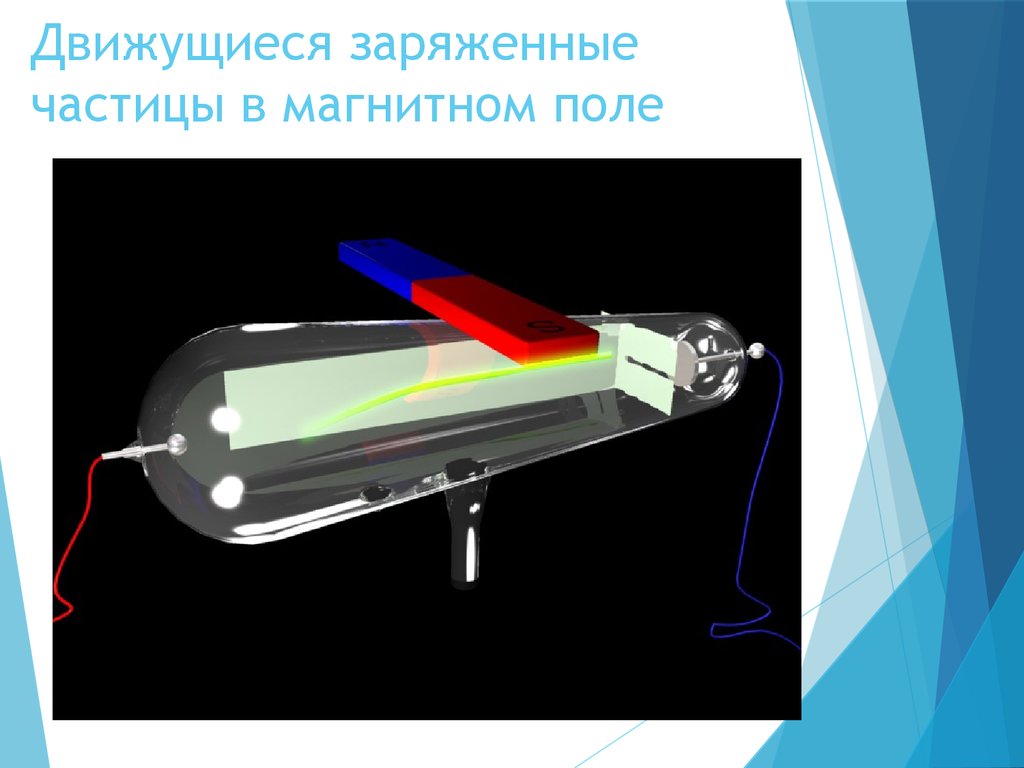
4. Движущиеся заряженные частицы в магнитном поле
5.
Радиационные пояса Земли. Быстрые заряженные частицыот Солнца (в основном электроны и протоны) попадают в
магнитные ловушки радиационных поясов. Частицы могут
покидать пояса в полярных областях и вторгаться в верхние
слои атмосферы, вызывая полярные сияния.
6.
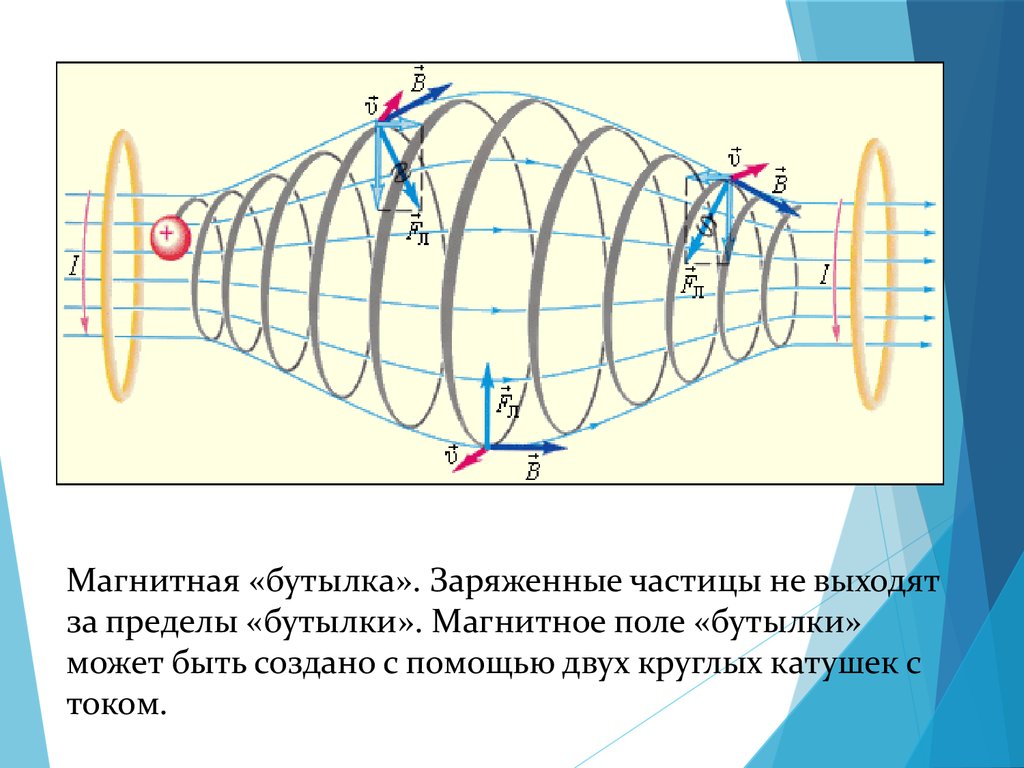
Магнитная «бутылка». Заряженные частицы не выходятза пределы «бутылки». Магнитное поле «бутылки»
может быть создано с помощью двух круглых катушек с
током.
7.
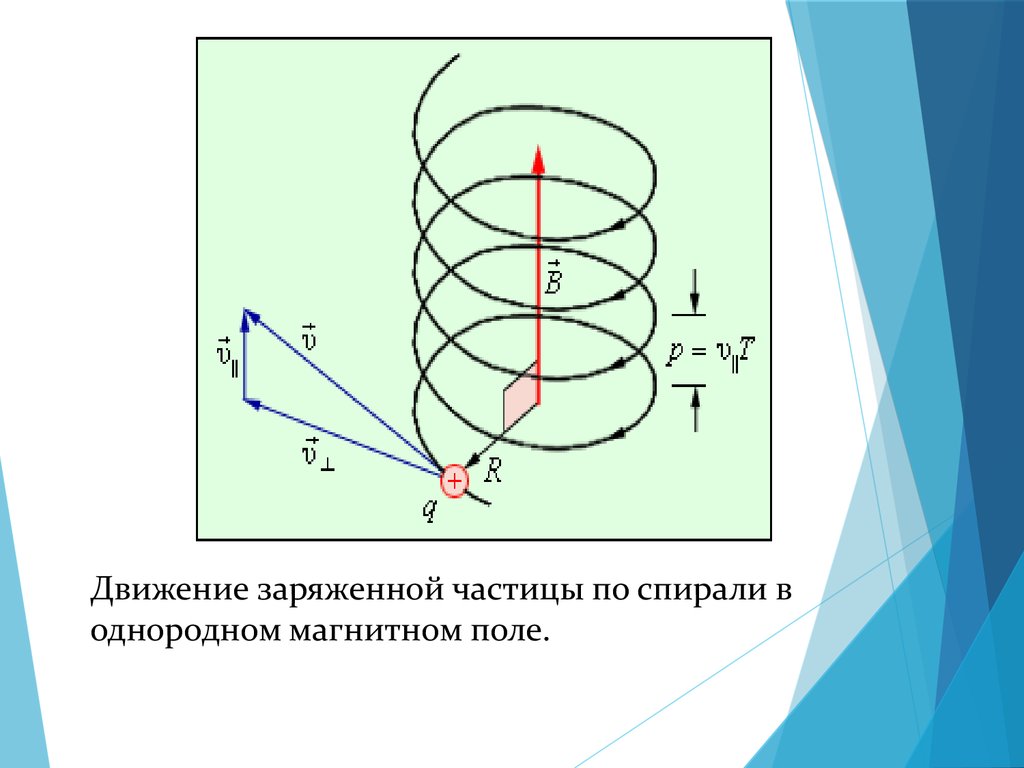
Движение заряженной частицы по спирали воднородном магнитном поле.
8.
Селектор скоростей и массспектрометр9.
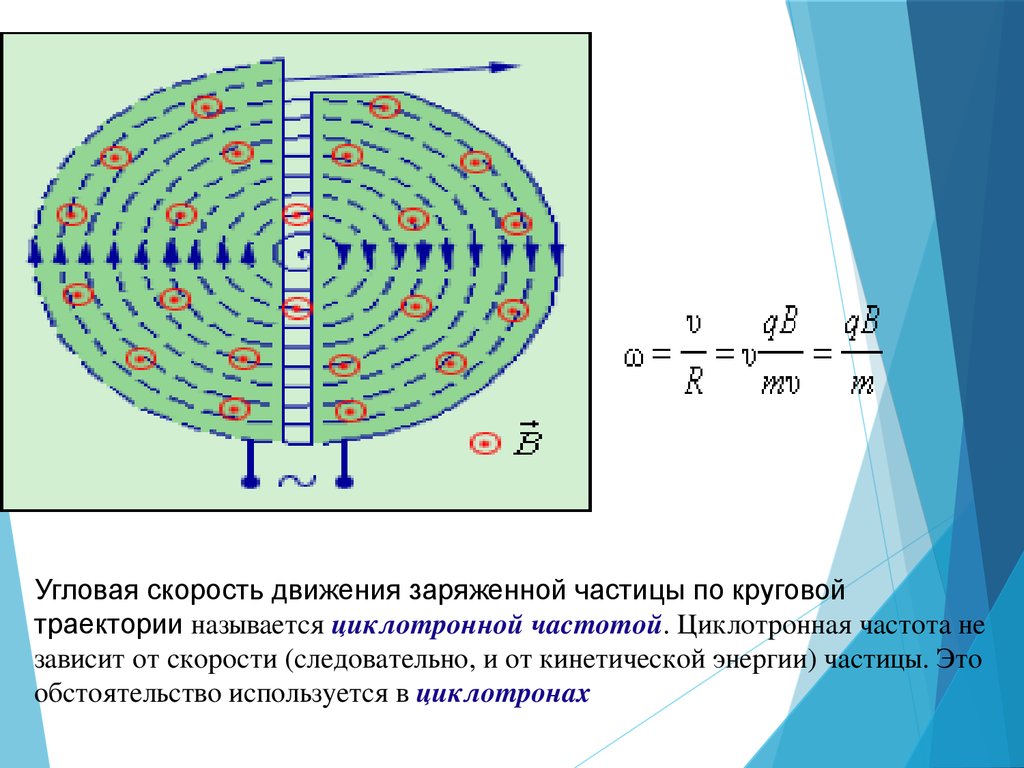
Угловая скорость движения заряженной частицы по круговойтраектории называется циклотронной частотой. Циклотронная частота не
зависит от скорости (следовательно, и от кинетической энергии) частицы. Это
обстоятельство используется в циклотронах
10. Использование действия магнитного поля на движущийся заряд
Использование действия магнитного
поля на движущийся заряд
Телевизионные
трубки: летящие к экрану
электроны отклоняются с помощью
магнитного поля
Ускорители
заряженных частиц для
получения частиц с большими энергиями
(циклотрон)
Масс-спектрограф-прибор,
позволяющий
разделять заряженные частицы по их
удельным зарядам, т.е. по отношению
заряда частицы к ее массе
11.
Радиускривизны траектории является
величиной постоянной
Данная
траектория является окружностью
2 r 2 m
T
qB
12. Движение заряженных частиц в магнитном поле
F qBa
m
m
2
a
r
qB 2
m
r
m
r
qB
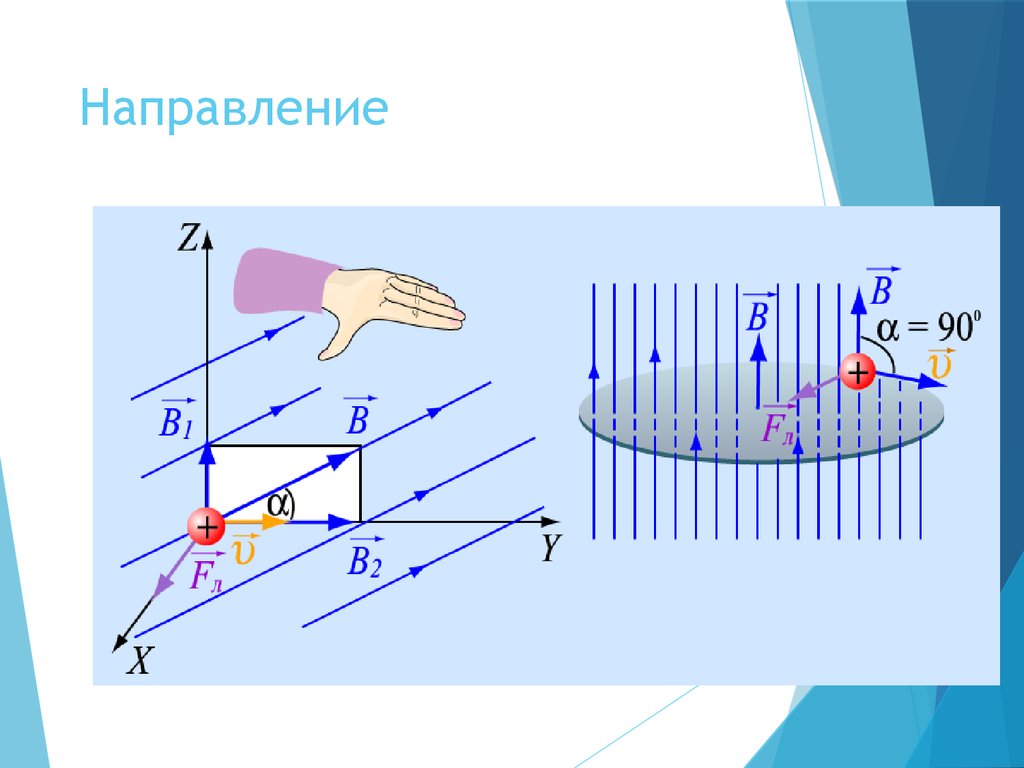
13. Направление
14. Модуль силы Лоренца
15.
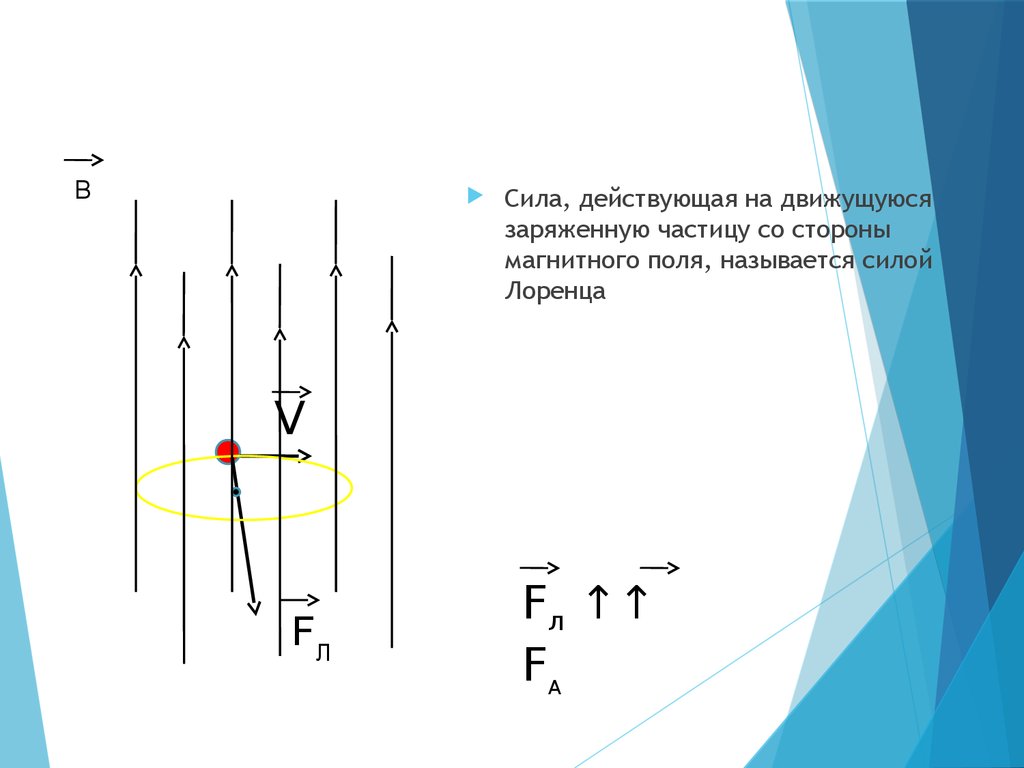
ВСила, действующая на движущуюся
заряженную частицу со стороны
магнитного поля, называется силой
Лоренца
V
FЛ
Fл ↑↑
FA
16. Модуль силы Лоренца
FАI
= ВIl sinα
V
Fл =
I=
V=
А
Л
ВIlFsinα
А
В
N
q
t
l
t
F
Fл =
Вql sinα
tN
; q0 =
Fл = Bq0V sinα
q
N
17.
Движение заряженной частицы под действием силы Лоренца, если α = 90°F ┴ V
В
V
Сила, перпендикулярная скорости,
вызывает изменение направления
движения.
Центростремительное ускорение:
a=
v
2
По II закону Ньютона F = m a
r
FЛ
ВqV = mV
r=
r
mV
Bq
2
18.
Движение заряженной частицы под действием силы Лоренца, если α = 90°Т.к движение равномерное, то
T=
В
т.к.
T=
2πr
V
r=
2πmV
BqV
mV
Bq
=
2πm
Bq
19. Применение силы Лоренца
ОсциллографКинескоп
Масс – спектрограф
Ускорители элементарных частиц (циклотрон, бетатрон,
синхрофазотрон)
B
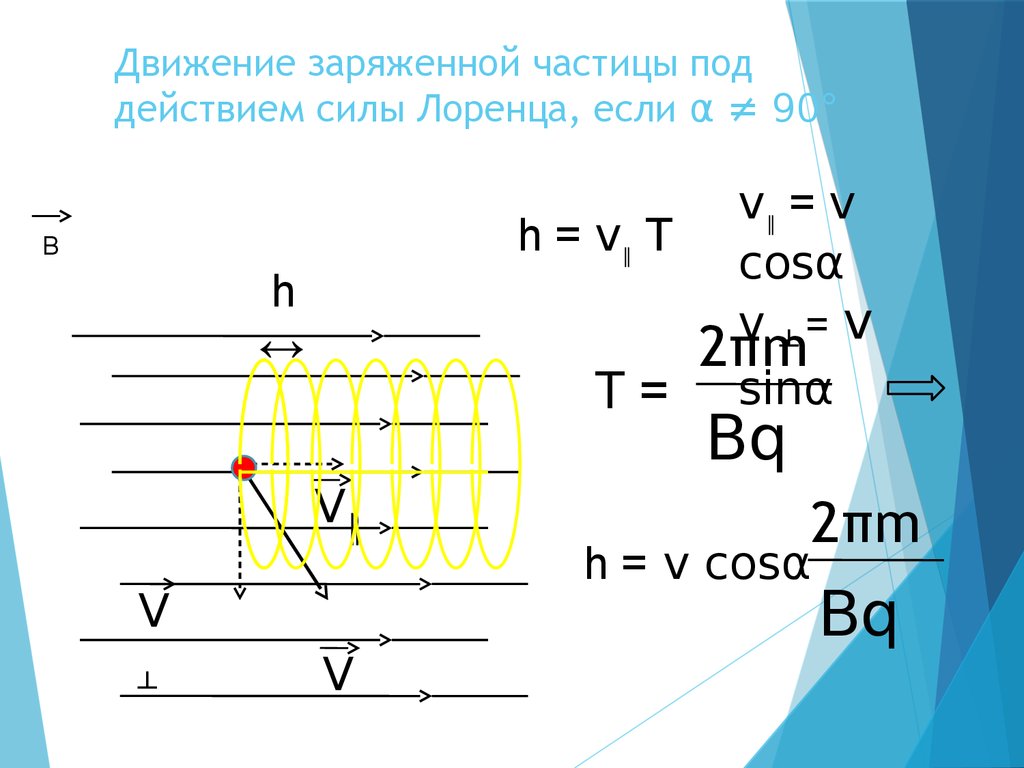
20. Движение заряженной частицы под действием силы Лоренца, если α ≠ 90°
v =vh=v T
cosα
v ┴= v
2πm
T = sinα
║
В
║
h
↔
Bq
V║
V
┴
V
2πm
h = v cosα
Bq


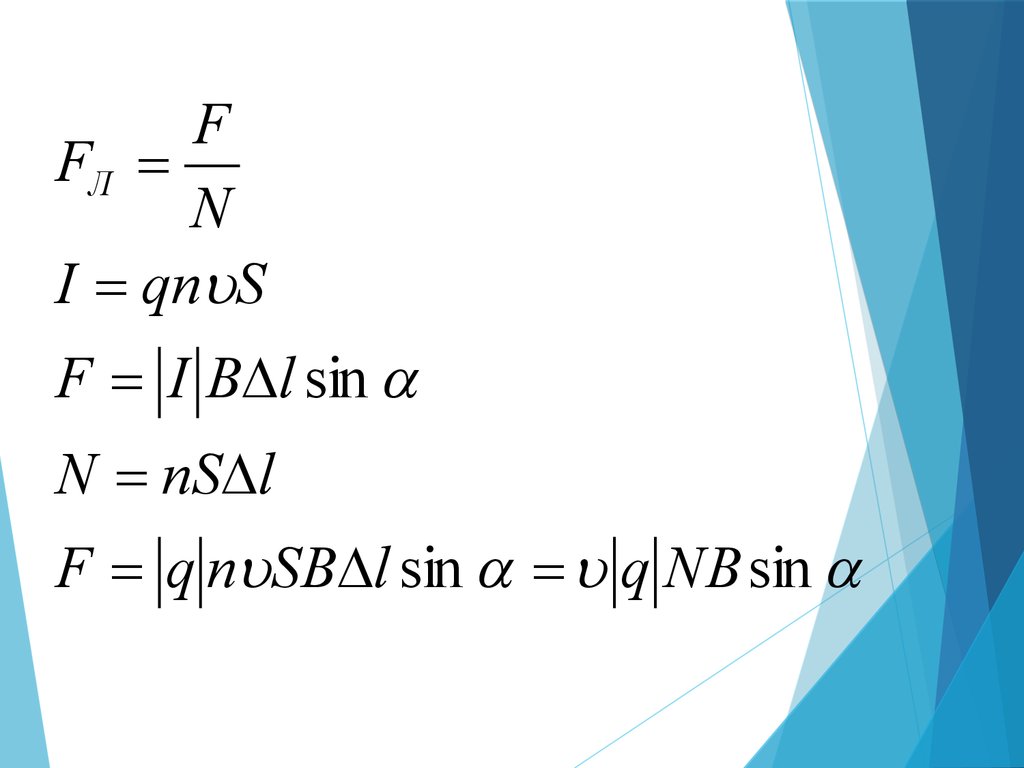









 physics
physics








