Similar presentations:
Электромагнитная индукция
1. Лекция № 9
ЭЛЕКТРОМАГНИТНАЯИНДУКЦИЯ
Литература:
Иродов
И.Е.
Электромагнетизм. Основные законы. —
М. — С.-П.: Физматлит, 2000.
2. Закон Фарадея. Правило Ленца
Явление электромагнитной индукции.В 1831 г. Фарадей экспериментально
обнаружил, что если через площадь,
охватываемую замкнутым проводником,
проходит переменный магнитный поток
(поток B ), то в проводнике возникает
индукционный ток.
3.
Правило Ленца: индукционный токвсегда
направлен
так,
чтобы
препятствовать причине его возникновения.
B
d
0
dt
Ii
d
0
dt
Ii
4.
Возникновение индукционного токаговорит о возникновении ЭДС индукции εi,
которая определяется законом Фарадея:
d
εi
,
dt
Bn dS
S
(9.1)
Возникновение εi не зависит от способа
изменения магнитного потока Ф, а зависит от
скорости его изменения. В СИ [Ф] = Вб
(вебер). Здесь направление нормали
n
к поверхности S связано с положительным
направлением обхода контура правилом
правого винта. Знак « » математическое
выражение правила Ленца.
5.
Способы изменения магнитного потока:• перемещение рамки или отдельных ее частей
в постоянном во времени магнитном поле;
• изменение во времени магнитного поля,
пронизывающего неподвижную рамку;
• меняются во времени и поле B ,
и
конфигурация или расположение контура в
поле.
6.
Электрическое поле индукционноговихревое:
εi El d l 0
тока
L
Потокосцепление Ψ (полный магнитный
поток) контура, содержащего более одного
витка алгебраическая сумма магнитных
потоков всех витков
N
i
(9.2)
i 1
Потокосцепление соленоида (в нем поток
через каждый виток одинаков, Фi = Ф1)
(9.3)
N 1,
где Ф1 поток через один виток соленоида, N
число его витков .
7.
Контур движется в постоянноммагнитном поле. Рассмотрим контур с
подвижной перемычкой.
B const
l
Ii
dS
Ii
dx
v
8.
Носители заряда движутся вместе сНа них
перемычкой со скоростью v .
действует магнитная сила Лоренца
FM || q v B,
B const
F M
F||M
u
E
F
v
FM || q v B,
напряженность
E FM || q v B
поле неэлектростатическое (сторонних сил).
Под действием этой силы заряды будут
перемещаться вдоль перемычки.
9.
На них также будет действоватьFM qu B
Ii
индукционный
ток.
Для
поддержания
постоянной
скорости
перемычки, надо приложить внешнюю силу
Fвнеш F FM
Элементарная работа магнитной силы
Лоренца
A FM ||u d t FM vd t q v Bu d t quB vd t 0
и работа внешних сил переходит в тепло
Aвнеш d Q
10.
ЭДС индукциисторонних сил
в
контуре
ЭДС
d S d
dx
εi E d l v Bl Bl
B
,
dt
dt
dt
где dS изменение площади,
охватываемой
замкнутым контуром, n B.
εi v Bl
11.
Контур покоится в переменноммагнитном поле.
B
B d S d S
εi E d l
(9.5)
t S
t
S t
L
Дифференциальная форма
B
rot E E
t
(9.6)
Электрическое
поле,
порождаемое
переменным магнитным полем, вихревое.
12.
Контур движетсямагнитном поле.
в
переменном
d
d BS
εi E d l
dt
dt
L
(9.7)
v B dl
t
13. Самоиндукция
Самоиндукция – возникновение εi вконтуре, по которому течет переменный
электрический ток I.
Переменный электрический
ток создает
переменное магнитное поле B
Меняется сила тока – пропорционально
меняется потокосцепление (B ~ I, Ψ ~ I)
LI ,
(9.8)
где L – индуктивность контура; зависит от
параметров окружающей среды (магнитной
проницаемости μ) и от геометрической
формы контура.
14.
ЭДС самоиндукцииd LI
dI
dL
d
εs
L
I
dt
dt
dt
dt
(9.9)
В частных случаях вторым слагаемым
можно пренебречь.
Найдем
индуктивность
бесконечно
длинного
соленоида,
поле
которого
однородно и сосредоточено внутри витков.
Индукция
B 0 H ,
где μ – магнитная проницаемость сердечника
в соленоиде.
15.
В соленоидеH nI NI l
где N – число витков, l – длина, n – число
витков на единицу длины соленоида.
B 0 nI 0 NI l
Поток магнитной индукции через один виток
соленоида
N
1 Bn d S Bn S BS 0 SI ,
(9.10)
l
S
где S – площадь витка соленоида, Bn =const.
16.
Потокосцепление соленоидаN2
SI
N 1 0
l
(9.11)
Индуктивность длинного соленоида
2
N
2
2
L 0
S 0 n lS 0 n V ,
l
(9.12)
где V – объем соленоида. В СИ [L] = Гн
(генри). 1Гн=1Вб/А.
17.
Если геометрические размеры соленоидане изменяются, N = const, вещество – не
ферромагнетик,
а
диамагнетик
или
парамагнетик, то L = const.
Тогда ЭДС самоиндукции соленоида,
согласно (9.9)
d
dI
εs
L
(9.13)
dt
dt
dI
0
dt
dI
0
dt
Ii
I
Ii
18.
Ток при включении и отключенииисточника ЭДС.
Сопротивление
L
R
источника
ЭДС
пренебрежимо мало.
K
ε
При установившемся токе
I0 ε R
При отключении источника ЭДС (при t = 0)
ток через индуктивность начнет убывать,
возникнет εs (противодействующая убыванию
тока)
dI
IR εs L ,
dt
19.
d I I Rdt L,t
R
dI
Rt
I L d t L d t ,
0
I0
0
I
I
R
ln t
I0
L
Тогда ток при отключении источника ЭДС
I I0
R
t
e L
ε
R
R
t
e L
20.
I tI0
I I0
R
t
e L
ε
R
R
t
e L
и
При
L 0, R L
при малых t
e
L 0
0
t
Rt L
очень быстро
стремится к
нулю.
Постоянная времени (время релаксации) –
время, в течение которого сила тока
уменьшилась в e (в экспоненту) раз:
L R
21. При включении источника ЭДС по закону Ома
dIIR ε εs ε L
dt
dI R
ε
I
dt L
L
Решение неоднородного ДУ 1-ого порядка –
сумма О.Р. однородного уравнения и Ч.Р.
неоднородного уравнения
I Ce
I 0 0
Rt L
I0
C I0
22.
Ток при включении источника ЭДСR
t
1 e L
I t
I0
0
I I0
R
t
ε
L
1
e
R
L 0
t
23. Взаимная индукция
Магнитный поток, пронизывающий контур 22 t ~ I1 t ,
2
1
I2
B
I1
В контуре 2 при L21 = const
2 L21I1,
L21 – взаимная
индуктивность
двух контуров
d I1
d
d 2
L21I1 L21
εi 21
dt
dt
dt
24.
1 t ~ I 2 t ,1 L12 I 2
В контуре 1 при L12 = const
d I2
d
d 1
εi12
L12 I 2 L12
dt
dt
dt
Здесь L12 и L21 – взаимные индуктивности
контуров, которые зависят от формы и
размеров
контуров,
их
взаимного
расположения и окружающей среды. Если
они неизменны, то L12 = const, L21 = const.
Всегда L12 = L21.
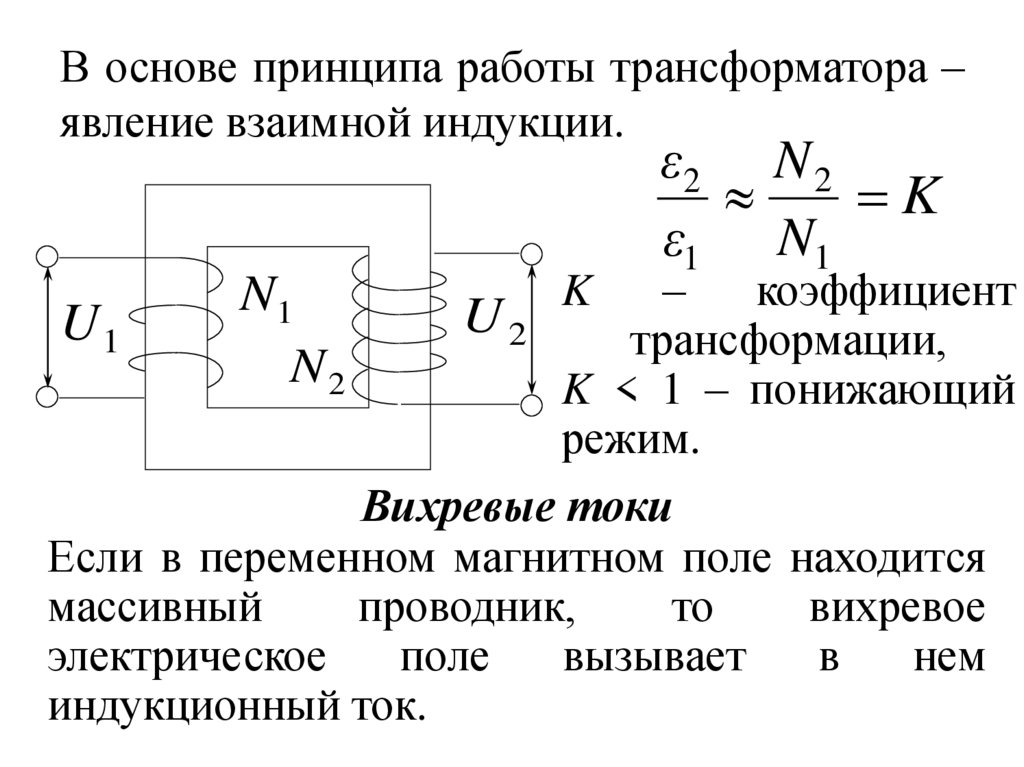
25. В основе принципа работы трансформатора – явление взаимной индукции.
ε2 N 2K
ε1 N1
–
коэффициент
U2
U1
трансформации,
K < 1 – понижающий
режим.
Вихревые токи
Если в переменном магнитном поле находится
массивный
проводник,
то
вихревое
электрическое
поле
вызывает
в
нем
индукционный ток.
N1
N2
K
26.
Плотность этого тока по закону ОмаТ.к. линии E
j E
замкнуты, то и линии тока
тоже замыкаются внутри проводника, такие
токи – вихревые токи.
Нагревание проводников вихревыми
токами
применяют
в
индукционных
металлургических печах для плавления
металлов и приготовления их сплавов.
Вихревые токи возникают также при
движении
массивных
проводников
в
магнитном поле.
27.
Взаимодействуяс
магнитным
полем,
вихревые токи вызывают появление сил,
действующих на движущееся проводящее
тело, которые согласно закону Ленца всегда
противодействуют движению.
Эти силы используются во многих
измерительных приборах (электрические
счетчики,
электромагнитное
успокоение
измерительных приборов, тахометры и др.)
Вихревые токи играют вредную роль в
железных сердечниках трансформаторов и
вращающихся
частях
электрических
генераторов, вызывая бесполезное нагревание
и снижая КПД этих устройств.
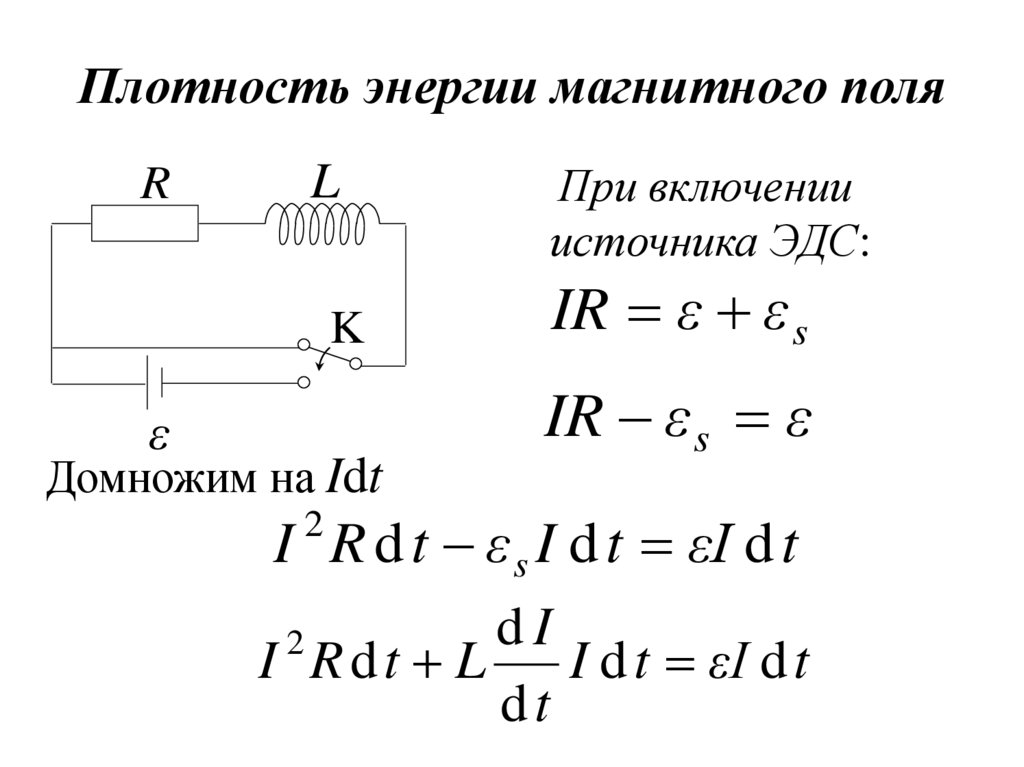
28. Плотность энергии магнитного поля
LR
K
ε
Домножим на Idt
При включении
источника ЭДС:
IR ε ε s
IR ε s ε
I R d t ε s I d t εI d t
2
dI
I Rdt L
I d t εI d t
dt
2
29. Элементарная работа сторонних сил за время dt
A A AA εI d t
Работа, идущая на создание магнитного поля
соленоида:
A εs I d t LI d I
на выделение джоулева тепла
A I 2 R d t d Q
30. Энергия магнитного поля контура (соленоида)
Энергиямагнитного
(соленоида)
поля
I
LI
W A LI d I
2
0
контура
2
Индуктивность длинного соленоида
2
N n 2lS n 2V
L 0
S
0
0
l
Его энергия
2
2
2
LI
N
I
W
0
S
2
l
2
31. В длинном соленоиде
NIB 0
l
NI
H
,
l
Энергия магнитного поля соленоида
LI
N I Sl 0 H
V wM V
W
0 2
2
2
2
l
2
2
2 2
Объемная плотность энергии магнитного
поля в длинном соленоиде, для изотропных
магнетиков
H
B
BH BH
0
wM
2
2 0
2
2
2
2
32. Энергия и силы в магнитном поле
Энергия неоднородного магнитного поля1
dW wM d V HBdV
2
1
1
2
W wM dV HBd V 0 H dV
2
2
V
V
V
Самостоятельно: Энергия и силы в
магнитном поле, Магнитное давление
(Иродов И.Е. Электромагнетизм. Основные
законы. — М. — С.-П.: Физматлит, 2000; стр.
267-272).






























 physics
physics








