Течение вязких жидкостей

1. Течение вязких жидкостей

Простые опыты:
Передача вращения через воздушный зазор

2.

3.

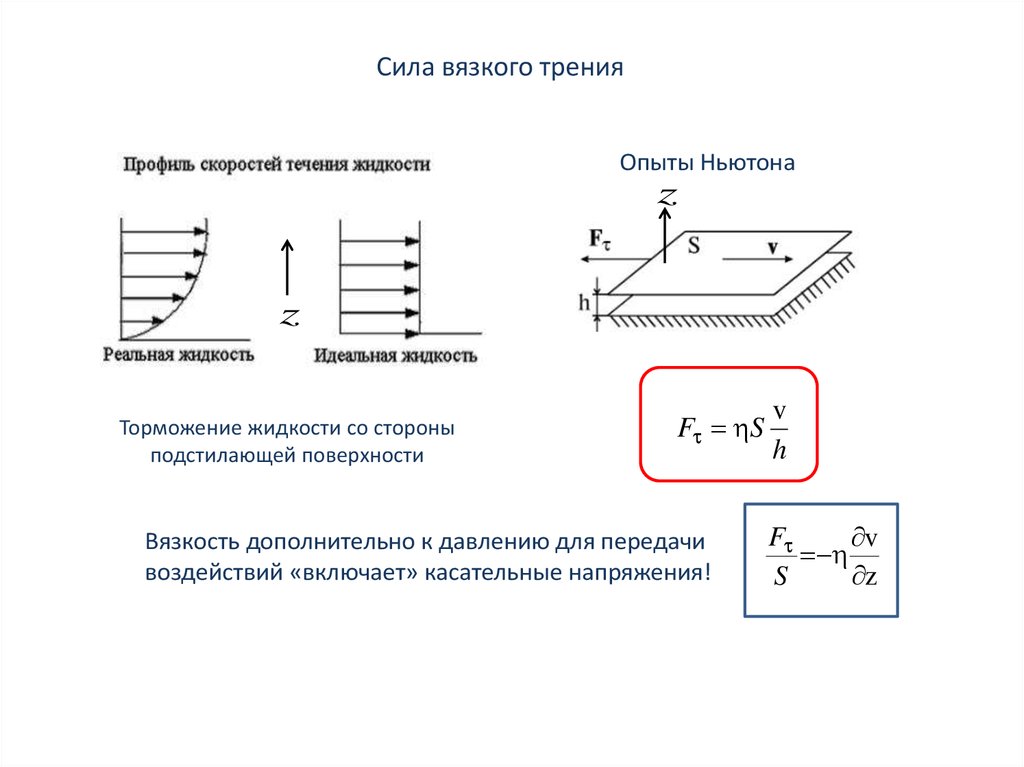
Сила вязкого трения
Опыты Ньютона
z
z
Торможение жидкости со стороны
подстилающей поверхности
F S
Вязкость дополнительно к давлению для передачи
воздействий «включает» касательные напряжения!
v
h
F
v
S
z

4.

Причина вязких сил – межмолекулярное взаимодействие
Молекулярно-кинетическое истолкование
силы вязкого трения
N
<v>верхн
<v>нижн
<v>верхн><v>нижн
В среднем за t происходит переход одинакового числа N молекул
между слоями. Но «верхние» молекулы имеют в среднем большую скорость
<v> по потоку, чем нижние и за t передают нижней части потока импульс p.
Соответственно, из-за этого изменения импульса по потоку верхний слой
тормозится нижним силой F p/ t – направлена вдоль
границы, так как характеризует изменение импульса по потоку.

5.

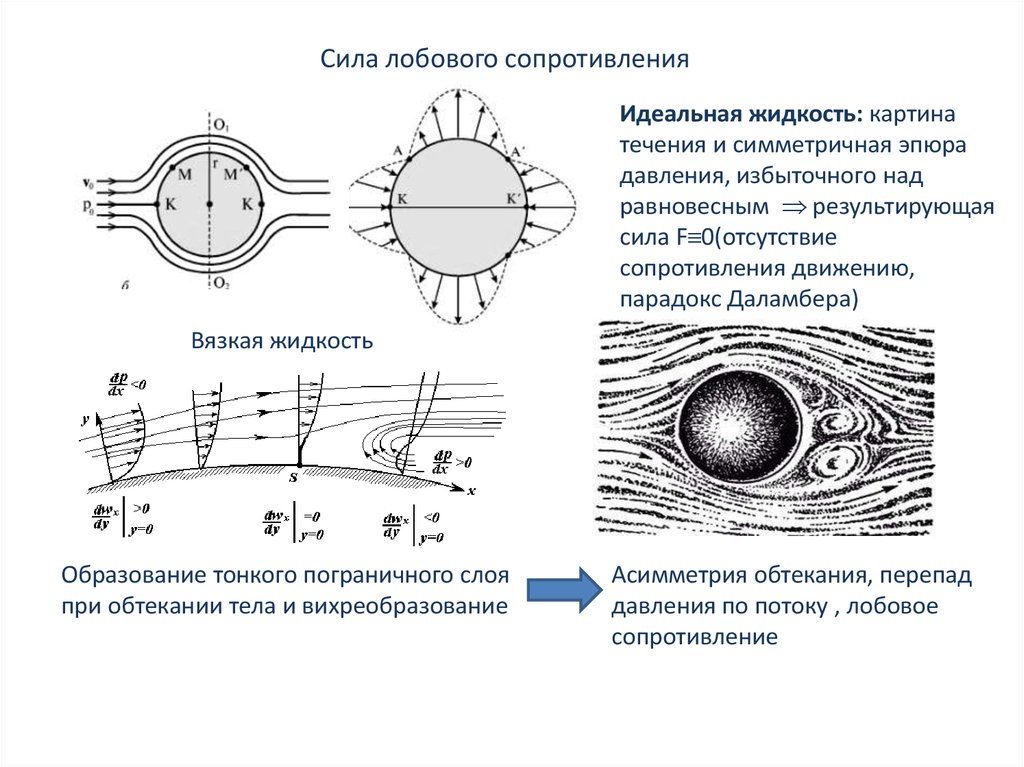
Сила лобового сопротивления
Идеальная жидкость: картина
течения и симметричная эпюра
давления, избыточного над
равновесным результирующая
сила F 0(отсутствие
сопротивления движению,
парадокс Даламбера)
Вязкая жидкость
Образование тонкого пограничного слоя
при обтекании тела и вихреобразование
Асимметрия обтекания, перепад
давления по потоку , лобовое
сопротивление

6.

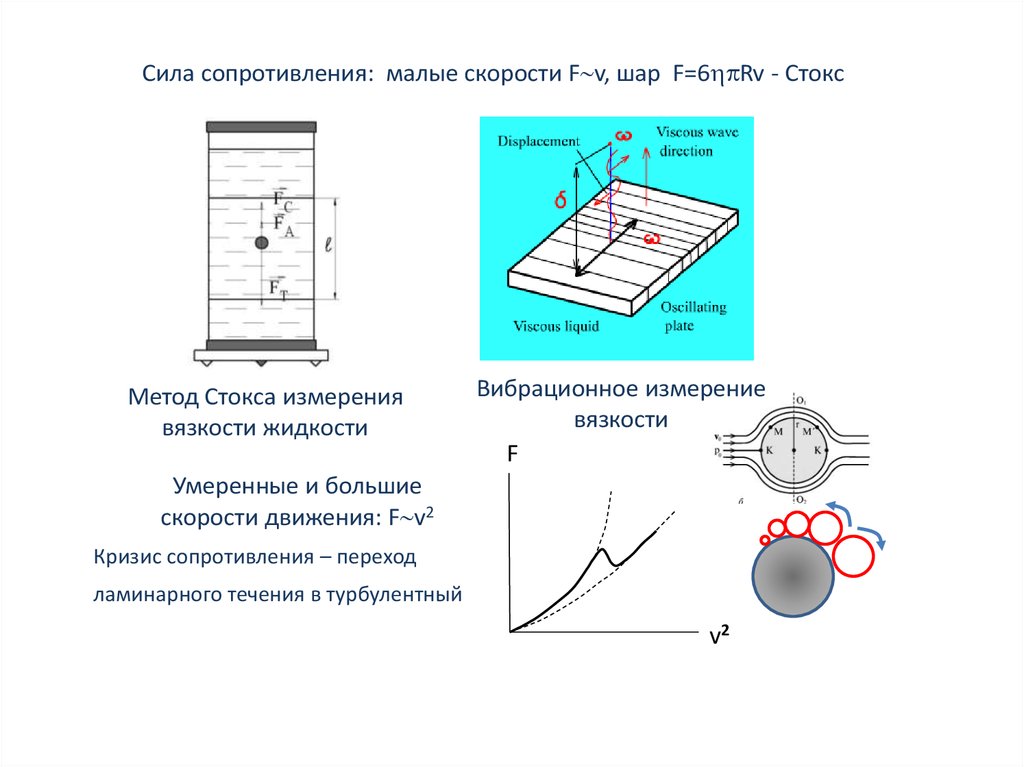
Сила сопротивления: малые скорости F v, шар F=6 Rv - Стокс
Метод Стокса измерения
вязкости жидкости
Вибрационное измерение
вязкости
F
Умеренные и большие
скорости движения: F v2
Кризис сопротивления – переход
ламинарного течения в турбулентный
v2

7.

Ламинарные и турбулентные течения
Ламинарное течение
Пуазейля в узких трубах
Число Рейнольдса
Фотография турбулентного течения
в трубе
сопоставляет масштаб проявления
сил инерции к силам вязкости
Падение напора из-за
силы сопротивления

8.

Дорожка Кармана при обтекании препятствия
Эоловы тона
Такомская катастрофа

9.

Неустойчивость Кельвина-Гельмгольца
Эффект Магнуса
неустойчивости: Рэлея-Тейлора, Мешкова-Рихтмайера

10.

2. Тензор плотности потока импульса,тензор напряжения
1)
Как учесть вязкость (вязкие силы Ньютона) в уравнениях
гидродинамики. В механике сила – результат изменения импульса за
время ее действия. В гидродинамике из-за
непрерывного распределения и течения вещества приходится
рассматривать не сам импульс, а связанную с ним величину –
- поток импульса, причем соотносить его единице объема среды,
т.е. рассматривать плотность потока импульса.
2)
Идеальная жидкость: плотность потока импульса
ik vi v k P ik
ik
- это тензор
который характеризует обратимый перенос импульса из-за
перемещения частиц жидкости и действия сил давления (2-ой член).
По смыслу P – сила, действующая на единицу площади по нормали
к ней. Сила вязкости – это тоже сила, действующая на единицу
площади поверхности, но только приложенная вдоль (касательно) к
поверхности. Основываясь на этой общности силы давления и
вязкости имеет смысл рассматривать с единой позиции.

11.

3) Еще отличие между P и F /S: давление характеризует внешнее
воздействие на выделенный элемент жидкости, поверхностные силы
вязкости, наоборот, характеризуют касательное, тормозящее воздействие
со стороны элемента жидкости на окружающие ее части по
разграничивающей поверхности.
x3 ( z )
При описании движения элемента
Р
жидкости необходимо
3
σ3
σ2
Р
σ1
x1 ( x )
2 Р
1
σi ( ix , iy , iz )
рассматривать силы, относящиеся
к элементу. Это силы вязкости и
x2 ( y ) силы , σ уравновешивающие
(по 3-му закону Ньютона) давление .
Для них, как и для касательных сил
вязкости , необходимо указывать
номер i оси нормальной к площадке
элемента. В свою очередь
компоненты каждого из векторов
также приходится нумеровать и вся их совокупность
образует тензор – тензор напряжения ik .

12.

Для идеальной жидкости имеем (с учетом антинаправленности
ik P )
ik P ik
ik vi v k ik
и тогда
Компоненты вязкостных сил также образуют своими
составляющими тензор ik , который называют тензором
вязких напряжений. При учете сил вязкости он добавляется
к тензору напряжений, т.е. переход от идеальной жидкости к
ik ik ik
вязкой заключается в замене
4)
Какой вид имеет тензор
ik
Основные соображения:
• Из наблюдений
вязкое трение проявляется
только при относительном перемещении слоев
жидкости, т.е.
vi
ik f
xk

13.

• Из закона Ньютона F v
S
z
эта зависимость
vi
(как правило) линейная: ik
xk
• При равномерном вращении с угловой скоростью const
жидкость движется как целое и вязкое трение отсутствует.
Поскольку v r , то добиться обнуления ik 0 можно
при условии, что тензор ik образуется обязательно
симметричной комбинацией производных компонент скорости
vi v k
v по координатам, т. е. ik
xk xi
В самом общем случае имеем (учет изотропии и вклада
сжимаемости)
vi v k 2
vl
vl
ik
ik
ik
xl
xl
xk xi 3

14.

5) Свойства тензора: симметричность
ik ki
Вследствие этого отсутствует необходимость рассмотрения
уравнения моментов.
Коэффициент вязкости и коэффициент второй вязкости ,
возникающей вследствие сжимаемости жидкости, всегда
положительны.
Современные тенденции – учет микроструктуры жидких сред
Эффективный тензор ik становится несимметричным,
Дополнительно к уравнению движения приходится рассматривать
уравнение моментов.

15.

3. Уравнение Навье-Стокса
Уравнение Навье-Стокса (Навье, 1827 г. - из модельных
представлений; Стокс, 1845 – не учел вторую вязкость)
обобщает ур-е Эйлера на случай (классических) вязких
жидкостей
ik
v
i
В обобщенном виде ур-е движения t
xk
ik P ik
с учетом выражений
и
vi v k 2
vl
vl
ik
ik
ik
xl
xl
xk xi 3
v
v
i v k i
xk
t
P
ik
xk
xk
P
xi
vi vk
x
k xi
дает
2
v
vl
ik l ik
3
x
x
x
l
k l
xi

16.

v
v
i vk i
xk
t
P
xi xk
vi vk
x
k xi
2
v
vl
ik l
3
x
x
x
l
i l
2 vi
vi
vi
P
vk 2 vl
vl
vk
x 2 x x 3 x x
t
x
x
x
x
k
i
i
k
i
l
i l
k
2vi
v
v
i v k i
xk
t
div v
xi
P
1
div v
2 vi ( )
xi
3 xi
v
( v ) v P 2 v ( ) div v
3
t