Similar presentations:
Динамика вязкой несжимаемой жидкости
1. Динамика вязкой несжимаемой жидкости
12. Предисловие
Рассматривается движение вязкойжидкости, плотность которой остается
неизменной.
В качестве исходных используем
уравнение Навье-Стокса и уравнение
неразрывности для несжимаемой
жидкости.
2
3. Задание
Вывести уравнение движения вязкойнесжимаемой жидкости – уравнение
Стокса.
Рассмотреть ламинарное
изотермическое течение несжимаемой
жидкости по горизонтальной трубе
постоянного поперечного сечения.
3
4. Словарь терминов
Несжимаемой называют жидкость,плотность которой не меняется.
Изотермическим называют поток,
температура которого остается
постоянной.
4
5.
56.
67.
78. Уравнение движения вязкой несжимаемой жидкости
Для вывода уравнения используем:уравнение неразрывности для
несжимаемой жидкости
divV 0
и постоянство вязкости жидкости при
изотермическом ее движении
const
8
9.
Уравнение Навье-Стокса при этих условияхdV
2
F grad p divV Div 2 V
dt
3
const;
divV 0; const
упрощается
dV
1
F grad p Div 2V
dt
где – коэффициент кинематической
вязкости.
9
10.
2u 2 v 2u 2 w 2ui
Div 2V 2
x 2 y x y 2 z x z 2
2u 2 v 2 v 2 w 2 v 2u 2 w 2 v 2 w 2 w
j
k
2
2
2 z y z 2 x z x 2 y z y 2
2
x y x 2
y
z
2 u 2 u 2 u u v w
i
x 2 y 2 z 2 x x y z
2 v 2 v 2 v u v w
j
x 2 y 2 z 2 y x y z
2 w 2 w 2 w u v w
k
x 2 y 2 z 2 z x y z
2 ui 2 vj 2 wk 2V
10
11.
и подставив ее в предыдущее выражение,получим уравнение Стокса – уравнение
движения вязкой несжимаемой жидкости
dV
1
2
F grad p V
dt
11
12.
Непосредственными наблюдениями имногочисленными опытами
установлено существование двух
основных режимов движения
жидкостей – ламинарного и
турбулентного.
12
13. Словарь терминов
Ламинарным называют строгоупорядоченное, слоистое (без
перемешивания) течение жидкости.
Единственной причиной потерь энергии
при таком движении в горизонтальных
трубах постоянного поперечного
сечения является трение, обусловленное
вязкостью жидкости.
13
14. Словарь терминов
При турбулентном режиме отдельныечастицы жидкости движутся по
произвольным сложным траекториям, в
результате чего струйки
перемешиваются и жидкость течет в
виде беспорядочной массы.
14
15.
Рис. Режимы течения жидкостейа) – ламинарный режим; б) – переход к турбулентному потоку;
в) и г) – различные формы развитого турбулентного течения
15
16. Ламинарное изотермическое течение несжимаемой жидкости в горизонтальной трубе постоянного поперечного сечения
1617.
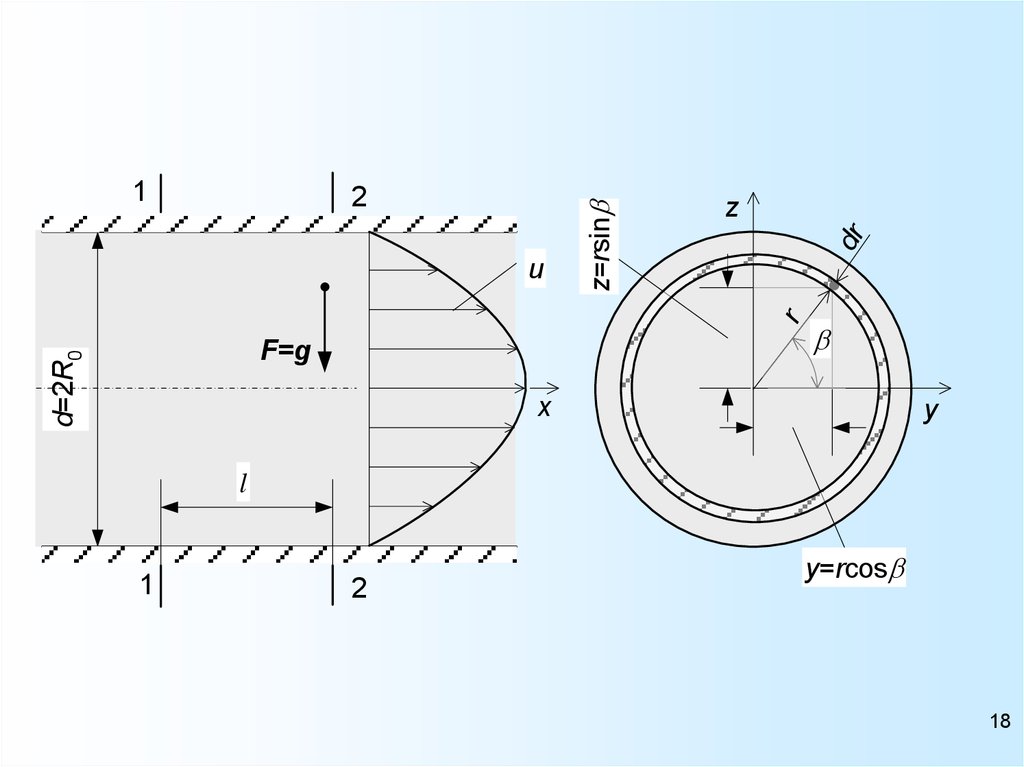
Предположим, что установившеесяламинарное движение жидкости
происходит в горизонтальной,
прямолинейной, круглой
цилиндрической трубе с внутренним
диаметром d 2R0 , что
соответствует одномерному течению.
На некотором расстоянии от входа в
нее, где поток уже сформировался
(стабилизировался), выделим отрезок
длиной l между сечениями 1-1 и 2-2.
17
18.
ru
z
dr
2
z=rsin
1
d=2R0
F=g
x
y
l
1
2
y=rcos
18
19.
Пусть в сечении 1-1 давление равно p1, а всечении 2-2 – p2 т.е. на длине l давление
в потоке изменилось на величину
p p1 p 2
за счет трения жидкости о стенки канала.
Применим к потоку жидкости уравнение
Стокса, которое в рассматриваемом
случае одномерного движения в
проекции на ось x примет вид
du
1 p
2
Fx
u.
dt
x
19
20. Выполним преобразование этого уравнения:
исключим выражение, стоящее в левойчасти уравнения, поскольку в
установившемся движении скорость не
меняется с течением времени,
следовательно
du dt 0
удалим первое слагаемое в правой части
уравнения, так как проекция силы
тяжести на горизонтальную ось x равна
нулю;
20
21.
в одномерном движении отсутствуютпроекции вектора скорости на оси
координат, перпендикулярные
направлению движения,
и
w 0
Поэтому и их производные равны нулю:
v 0
v y 0
и
w z 0.
Следствием этого для несжимаемой
жидкости будет
u v w
u
u
divV
0
0 и
0
2
x y z
x
x
2
21
22.
Проекция уравнения Стокса на ось x приметследующий вид
2
2
1 dp
u u
2 2
dx
z
y
Изменение давления вдоль трубы
пропорционально длине трубы
p 2 p1
dp
p
const
dx
l
l
поэтому получим
u u
p
y 2 z 2
l
2
2
22
23.
Решим полученное дифференциальноеуравнение при условии, что на границе
области течения (на стенке трубы)
скорость частиц жидкости равна нулю
u гр 0
Граница области течения описывается
уравнением окружности
y z
2
гр
2
гр
R
2
0
23
24.
Решением дифференциального уравненияявляется функция
u AR y z
2
2
2
0
Она удовлетворяет граничному условию,
а при
p
A
4 l
превращает дифференциальное уравнение
в тождество.
24
25.
Это становится очевидным послеподстановки данной функции в
дифференциальное уравнение
2
2
2
2
2 A R02 y 2 z 2
A R0 y z
2
2
y
z
p
2 A 2 A
l
25
26.
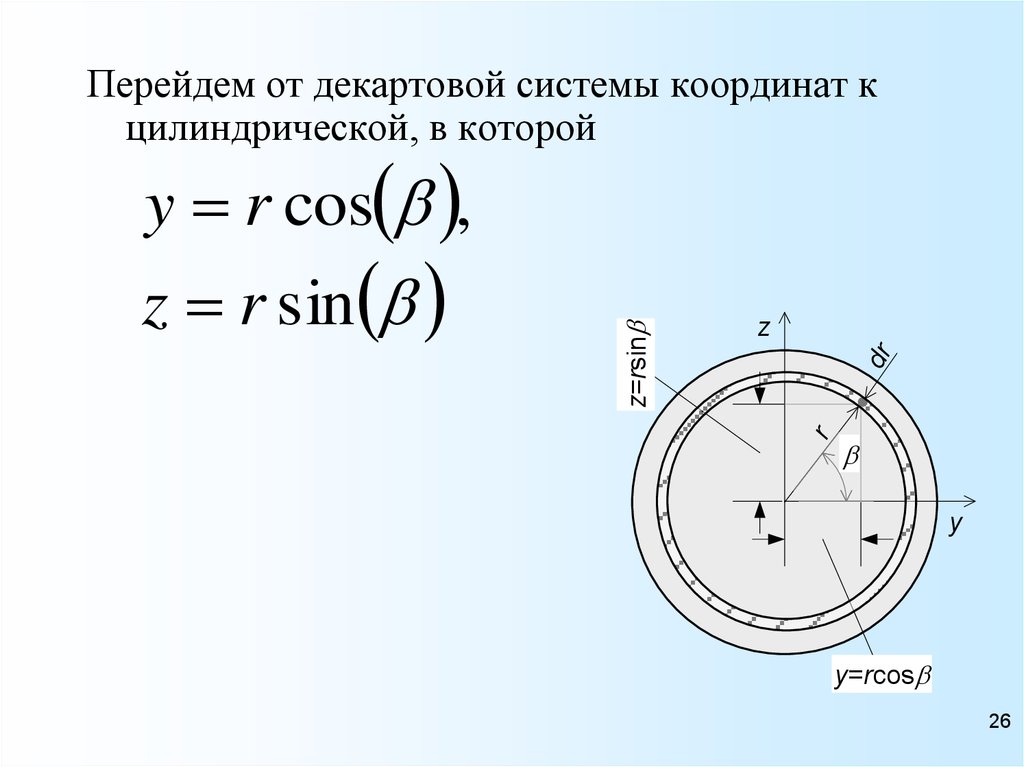
Перейдем от декартовой системы координат кцилиндрической, в которой
r
u
z
dr
z 1 r sin 2
z=rsin
y r cos ,
d=2R0
F=g
x
y
l
1
2
y=rcos
26
27.
Уравнение одномерного движениянесжимаемой жидкости в этой системе
координат
p 2
2
2
u
R0 y z
4 l
p 2
R 0 r 2 cos 2 r 2 sin 2
4 l
2
pR
p 2
r
2
1
R0 r
4 l
4 l R 0
описывается квадратичной зависимостью
скорости частицы жидкости от радиуса.
2
0
27
28. Словарь терминов
12
u
z=rsin
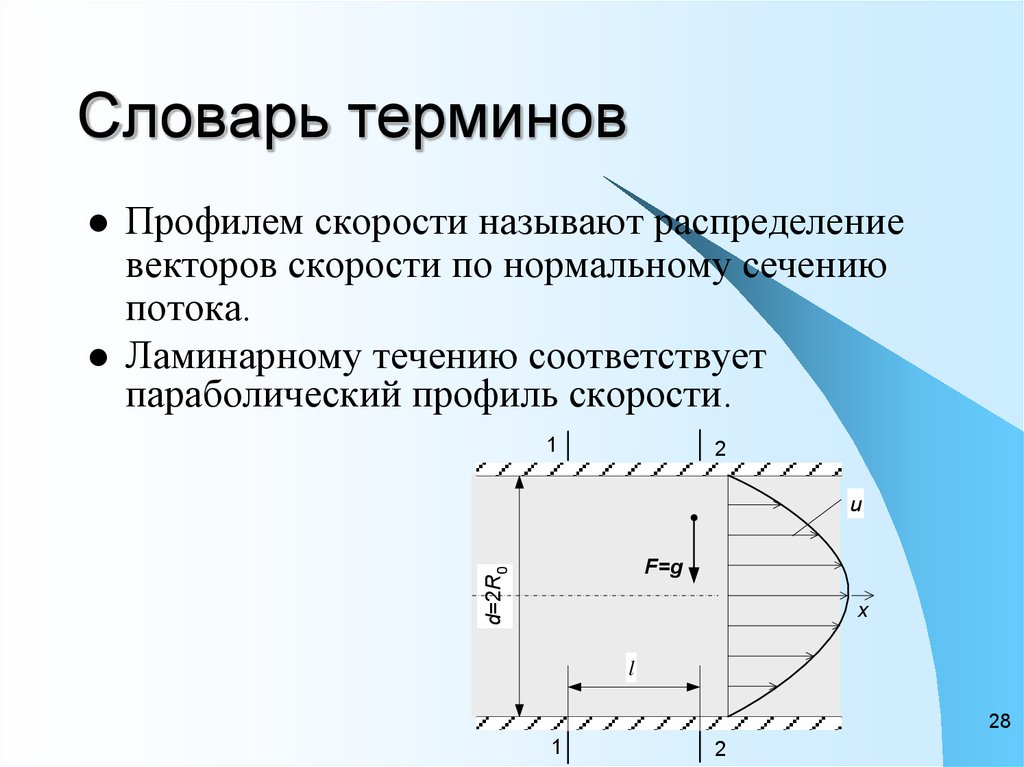
Профилем скорости называют распределение
векторов скорости по нормальному сечению
потока.
Ламинарному течению соответствует
параболический профиль скорости.
z
F=g
d=2R0
x
l
28
1
2
29.
Максимальная скорость имеет место вцентре сечения трубопровода (при r=0)
u max
pR
4 l
2
0
Применим полученный закон
распределения скоростей для расчета
объемного расхода жидкости.
Элементарный расход через бесконечно
малую площадку dS равен
dQ udS
29
30.
d=2R02
r
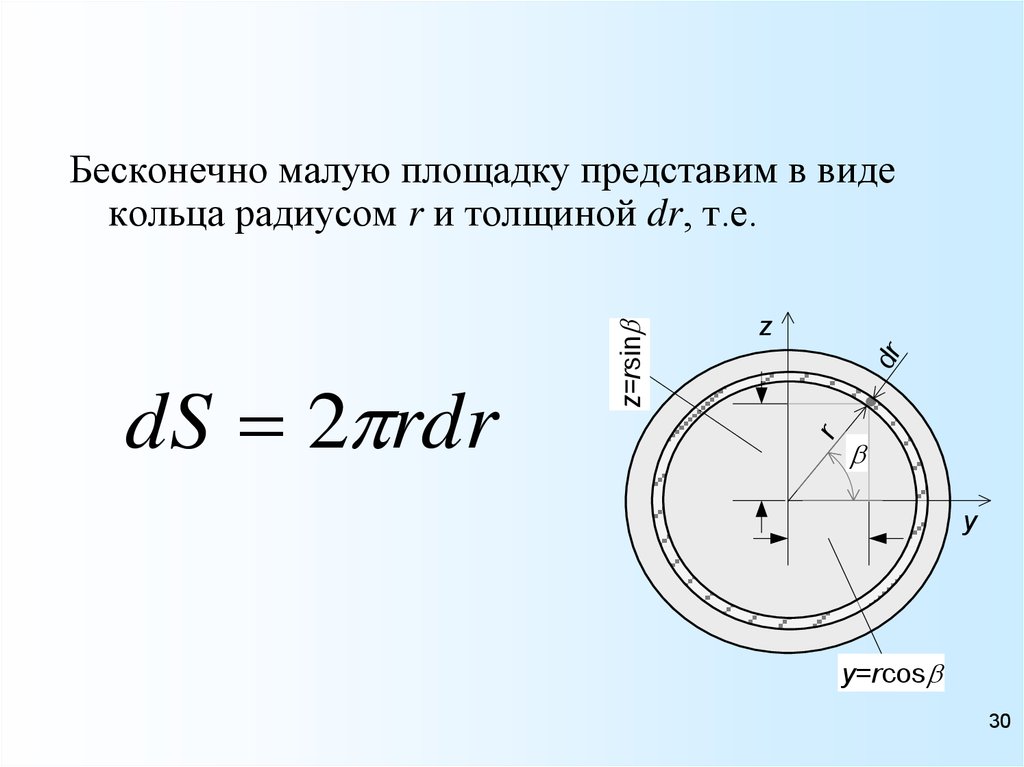
dS 2 rdr
u
z
dr
1
z=rsin
Бесконечно малую площадку представим в виде
кольца радиусом r и толщиной dr, т.е.
F=g
x
y
l
1
2
y=rcos
30
31.
Тогда после интегрирования по всейплощади поперечного сечения, т.е. от
r=0 до r=R0, получим
R0
Q udS u 2 rdr
S
2 p
4 l
0
R
R0
2
0
r rdr
2
0
pR
8 l
4
0
31
32.
Среднюю по сечению скорость находимделением расхода на площадь
поперечного сечения канала
u ср
p 2
R
0
2
R0 8 l
Q
Ее значение в два раза меньше найденной
ранее максимальной скорости на оси
трубы.
32
33.
Преобразовав полученное выражение,найдем закон сопротивления, т.е.
зависимость потери давления на трение
от расхода, либо средней скорости
жидкости, ее вязкости и геометрических
размеров канала
p
8 lQ
R
4
0
8 lu ср
R
2
0
33
34.
Из уравнения следует, что потеридавления при ламинарном течении
жидкости по прямолинейному каналу
цилиндрической формы прямо
пропорциональны его длине, расходу и
вязкости среды в первой степени и
обратно пропорциональны радиусу
(диаметру) в четвертой степени. В
литературе этот закон носит имя
Пуазейля.
34
35.
Выразив радиус трубы через диаметр, ивыполнив ряд эквивалентных
преобразований, данный закон можно
представить в виде
p
8 lu ср u ср
2
d
u ср
2
64 l u
du ср d 2
2
ср
64 l u
Re d 2
2
ср
где
Re u ср d – критерий Рейнольдса.
35
36. Словарь терминов
В технических расчетах принято потеридавления на трение рассчитывать по
формуле Дарси-Вейсбаха
l u
p l
d 2
2
ср
где l – коэффициент потерь на трение.
36
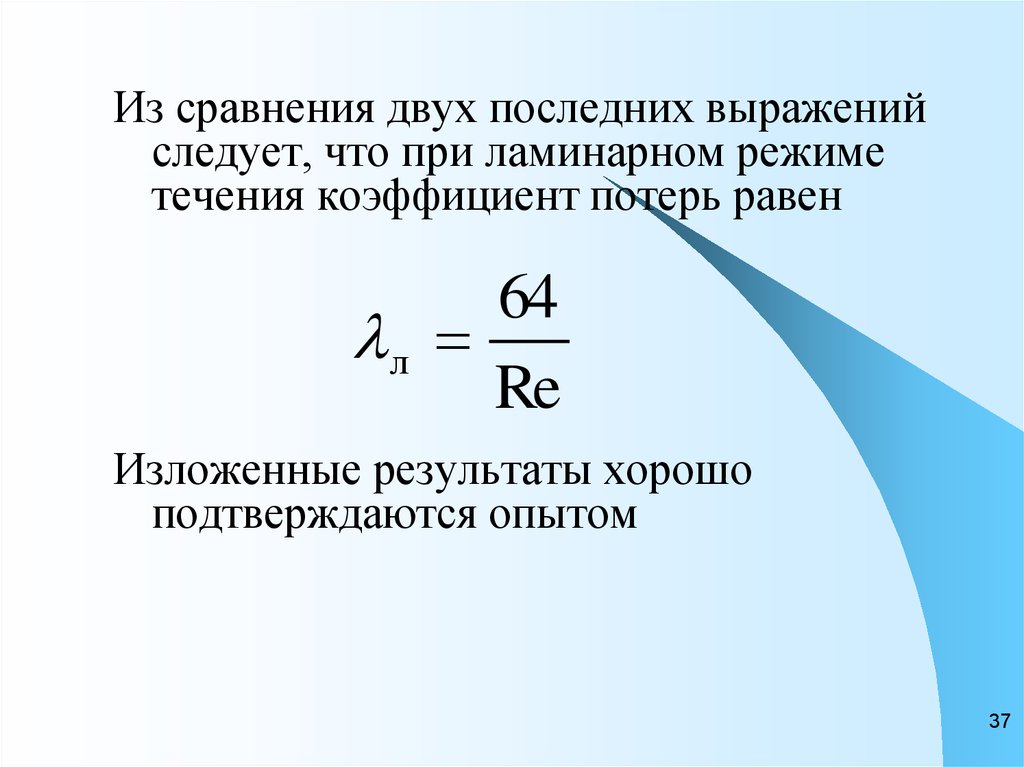
37.
Из сравнения двух последних выраженийследует, что при ламинарном режиме
течения коэффициент потерь равен
64
lл
Re
Изложенные результаты хорошо
подтверждаются опытом
37
38. Исключения:
течение на начальном участке трубы,где еще происходит формирование
потока;
течение с теплообменом;
течение в капиллярах и зазорах, где
имеет место облитерация;
течение с большими перепадами
давлений.
38

































 physics
physics








