Similar presentations:
Динамика вязкой жидкости
1.
Динамика вязкой жидкостиВязкая жидкость
–жидкость,
обладающая
свойством
вязкости,
т.е., свойством
Вяз́ кость
(внутреннее
трение)
— свойство
жидкостей
оказывать
́
́
реальных жидкостей,
оказывающим
сопротивление
перемещению
сопротивление
перемещению одной
их части относительно
другой. одной части
жидкости относительно другой.
Движение вязкой несжимаемой ньютоновской жидкости описывается
уравнением Навье-Стокса, в левой части которого стоит полная производная
от скорости по времени, в правой сумма напряжений действующих сил
(силы тяжести, силы давления, вязких сил)
Уравнение Навье-Стокса
u
p
(
u
)
u
F
u
t
2.
Простейшие примеры течений вязкой жидкостиI. Движение жидкости между плоскостями, одна из которых
(пластина 1) движется со скоростью u0
y
h
u0
Пластина 1
ux=u(y,t)
0
x
Пластина 2
Проекция уравнения Навье -Стокса на
ось х
Проекция уравнения Навье-Стокса на
ось y
Течение стационарно,
одномерно и зависит
только от y
u
p
(
u
)
u
F
u
t
2u
2 0
y
p
0 (2)
y
Уравнение непрерывности удовлетворяется тождественно
(1)
3.
I. Движение жидкости между двумя плоскостями (продолжение)Решение:
Из (2)
p const
u ay b
Граничные условия:
u=u0 при y=h
a=u0 /h
u=0 при y=0
b=0
y
u u0
h
Распределение
скоростей между
пластинами линейно
Сила трения, действующая на пластины
u
u
0
(
y
o
)
j
yx
y
h
y
0
u
0
(
y
h
)
(
j
)
yx
h
y
h
Суммарная сила на жидкость =0
y
u0
- yx
yx
x
4.
II. Движение жидкости между двумя неподвижнымиплоскостями
y
Жидкость течет за счет силы градиента давления dp/dx
h
Течение стационарно и
одномерно, т.е. uy =0 ux=u(y,t)
ux=u(y,t)
0
x
Уравнение Навье Стокса на ось y :
Уравнение Навье Стокса на ось x :
p
0
y
2ux 1 p
2
y
x
Это выполняется только если dp/dx= const !
p=p(x)
Левая часть ур.
зависит только
от y, а правая –
только от x
5.
II. Движение жидкости между неподвижными плоскостями (продолжение)2
1dp
u
1dp
2
x
u
y
ay
b
const
x
2
2
dx
y
dx
Граничные условия:
b=0
u x=0 при y=0, y=h
h dp
a
2 dx
Решение с учетом гран. условий
1dp
u
y
(y
h
)
x
2
dx
Течение имеет параболический профиль
Сила, действующая на плоскость
Средняя скорость
h
2
1
h
dp
u
u
(
y
)
dy
x
сред
x
h
12
dx
0
u h
dp
(y
o
)
yx
y
dx
y
0 2
6.
III а. Течение вязкой жидкости по трубе кругового сеченияВ полярных координатах: r,
1
p
(
r u
)
x
r
r
r
l
θ, x
p2
u
r
a
ln
r
b
x
4
l
Решение
Скорость конечна во всем сечении трубы, поэтому a=0
Гран. Условие при r=R
: ux=0
b
p 2
R
4 l
p 2 2
u
R
r
x
4
l
Расход жидкости – масса жидкости, протекающая в единицу времени
через сечение трубы
p4
Q
2
ru
(
r
)
dr
R
8
l
0
R
Формула Пуазейля
7.
III б. Течение вязкой жидкости по трубе эллиптического сеченияТруба эллиптического сечения
z
y2 z2
2 1
2
a b
y
Общее решение
2
2
u
u
dp
x
x
u
(
)
y
,
zx
2
2
dx
y
z
2
2
u
Ay
Bz
C
x
Решение должно удовлетворять гран.
условию: u=0 на эллипсе, т.е.
2
2
u
Ay
Bz
C
0
x
22
2
2
pa
b y
z
u
2 2(
1
)
x
2
2
2
la
b ab
При b или a
переходим к случаю 2-х
параллельных плоскостей
p 2 2
u
R r
x
4
l
8.
Предельный переход от трубы эллиптического сечения к параллельнымплоскостям (b>>a)
y
y’
2
2
2
2
2 2
2
p
a
b
y
p
a
b
y
p
y
2
u
(
1
)
(
1
)
a
(
1
)
x
2
2 2
2
2
2
2
l
a
b
a
2
l
b
a
2
l a
h
h/2
ux=u(y,t)
0
Было решение для двух плоскостей
y y h/2
'
1dp
u
y
(y
h
)
x
2
dx
2
1
p
h
y
'2
u
[
1
2
]
x
2
l 4 (
h
/
2
)
9.
Уравнение Навье –Стокса с потенциальнымисилами
u
p
(
u
)
u
F
u
t
F U
1 2
(
u
)
u
(
u
)
[
u
rot
u
]
2
2
uu
p
(
U
)
[
u
rot
u
]
u
t
2
Стационарное течение жидкости
Умножаем скалярно на
элемент линии тока, dr // u
2
u
p
(
U
)
[
u
rot
u
]
u
2
2
u
p
d
(
U
)
d
r
u
2
10.
2u
p
d
(
U
)
d
r
u
2
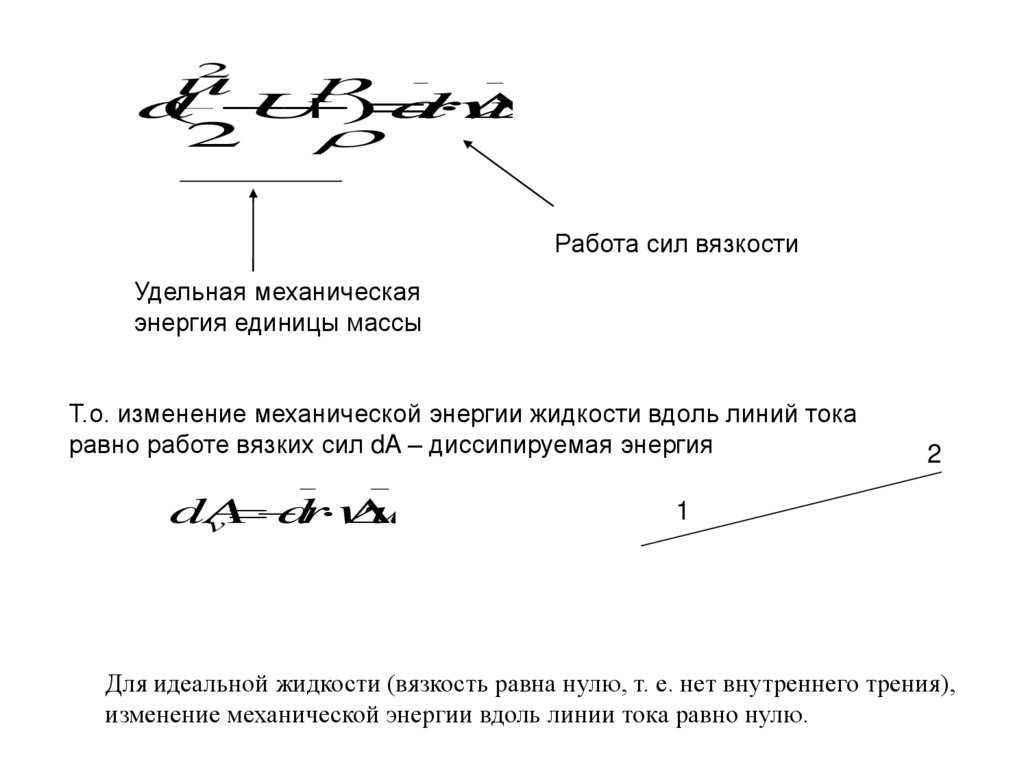
Работа сил вязкости
Удельная механическая
энергия единицы массы
Т.о. изменение механической энергии жидкости вдоль линий тока
равно работе вязких сил dA – диссипируемая энергия
dA
dr
u
v
2
1
Для идеальной жидкости (вязкость равна нулю, т. е. нет внутреннего трения),
изменение механической энергии вдоль линии тока равно нулю.









 physics
physics








