Similar presentations:
Гидростатика. Поверхностные явления. Гидромеханика идеальной и вязкой жидкости. Практическое занятие 5
1.
Практическое занятие 5Гидростатика.
Поверхностные явления.
Гидромеханика идеальной и вязкой жидкости.
Давление силы на поверхность
Fn
p
S
H
p 2 Па
м
Сила давления на
поверхность
независимо от
природы силы:
перпендикулярна
поверхности тела
в любой точке тела
F pS
Действует на тело
«снаружи»
1
2.
Закон ПаскаляДавление, производимое на поверхность жидкости
(газа), передается во все точки жидкости (газа)
без изменения
Абсолютное давление (следствие) складывается
из «внутренних» давлений, обусловленных
свойствами системы (внутренние причины) и внешнего
атмосферного давления (внешняя причина)
pабс. p0 pBH.
2
3.
Суммарное «внутреннее» давление –избыточное над атмосферным.
Измеряется манометром.
pизб . pBH.
Часто составляющие абсолютного давления измеряются
во внесистемных единицах:
1 мм рт.ст. 13600 9,81 10 3 133 Па
1 ммвод.ст. 1000 9,81 10 3 9,81 Па
Атмосферное давление измеряется барометром
Нормальное атмосферное давление:
p0 105 Па 760 мм рт.ст.
Абсолютное давление:
pабс. p0 pизб .
3
4.
Пример:абсолютное давление
на глубине h в водоеме
p0
Абсолютное давление
(основное уравнение
гидростатики):
pабс. p0 gh
h
«Внутреннее» гидростатическое
давление: p . p С gh
«Внешнее» атмосферное
давление: p0
4
5.
На какой глубине в водоеме давление в 2 разабольше нормального (атмосферного)?
Атмосферное давление:
р0 105 Па
Абсолютное давление на глубине h:
pабс. p0 gh
pабс. p0 gh
gh
1
2
p0
p0
p0
5
p0
10
h
3 10 м
g 10 10
5
6.
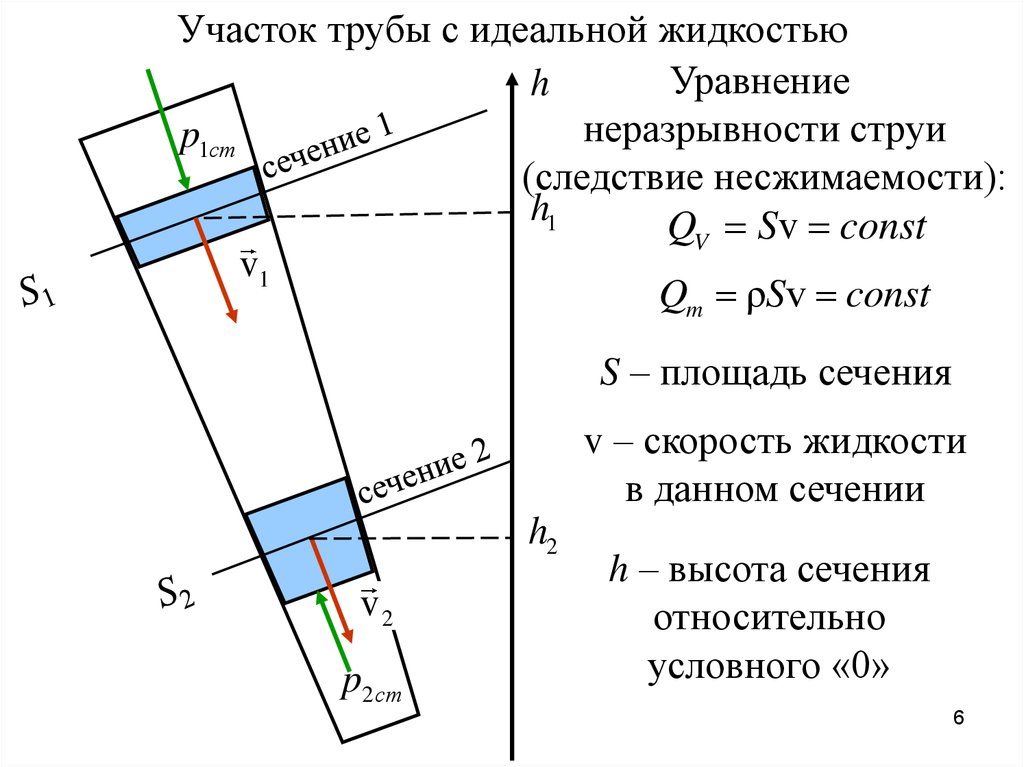
Участок трубы с идеальной жидкостьюУравнение
h
неразрывности струи
p1ст
(следствие несжимаемости):
h1
QV Sv const
v1
Qm ρSv const
S – площадь сечения
v – скорость жидкости
в данном сечении
h2
v2
p2ст
h – высота сечения
относительно
условного «0»
6
7.
Составляющие абсолютного давления:pабс. p0 pизб .
Атмосферное давление:
p01 p02 p0
Составляющие избыточного давления:
1. рст. – статическое давление на выделенное сечение
«снаружи», связанное с работой по
перемещению объема жидкости против сил давления
7
8.
Трубопровод«источник»
v1
«остаток системы»
рст.1
рст.2
v2
рст.1 – статическое давление со стороны «источника»
рст.2 – статическое давление со стороны
«остальной» части системы (противодавление)
2. рдин. – динамическое давление связанное с движением
(кинетической энергией движения) жидкости:
2
2
m
v
ρv
pдин.
2
2
8
9.
3. рГС – гидростатическое давление, связанное сположением сечения относительно условного «0»
(потенциальной энергией положения):
h
p С gh
mgh
Суммарное избыточное давление в данном сечении:
pизб . pBH. рст. рдин. рГС
9
10.
Жидкость идеальная →→ нет потерь давления:
ризб .1 ризб .2 const
ризб .1
ризб .2
Уравнение Бернулли (закон сохранения энергии):
ρv
ρv
pст.1
ρgh1 pст.2
ρgh2 const
2
2
2
1
2
2
10
11.
Система кровообращения человека обладаетминимальным сечением
в области аорты, равным примерно 8 см2 ,
и максимальным сечением в области капилляров.
Оцените примерную суммарную
площадь сечения капилляров в теле человека
и общее их количество, если скорость
течения крови уменьшается от 0,5 м/с
в аорте до 0,001 м/с в капиллярах.
Диаметр капилляра считать равным 10-5 м.
Эластичностью сосудов пренебречь.
11
12.
СИ:S 8 10 4 м 2
vA = 0,5 м/с
vK = 0,001 м/с
Уравнение неразрывности:
v S
S
v S v S
v
S
dK = 1·10-5 м
0,5 8 10 4
0,4м 2
0,001
S 4 S
N
2
πd
πd 2
4
N
4 0,4
3,14 1 10
5 2
5 109
12
13.
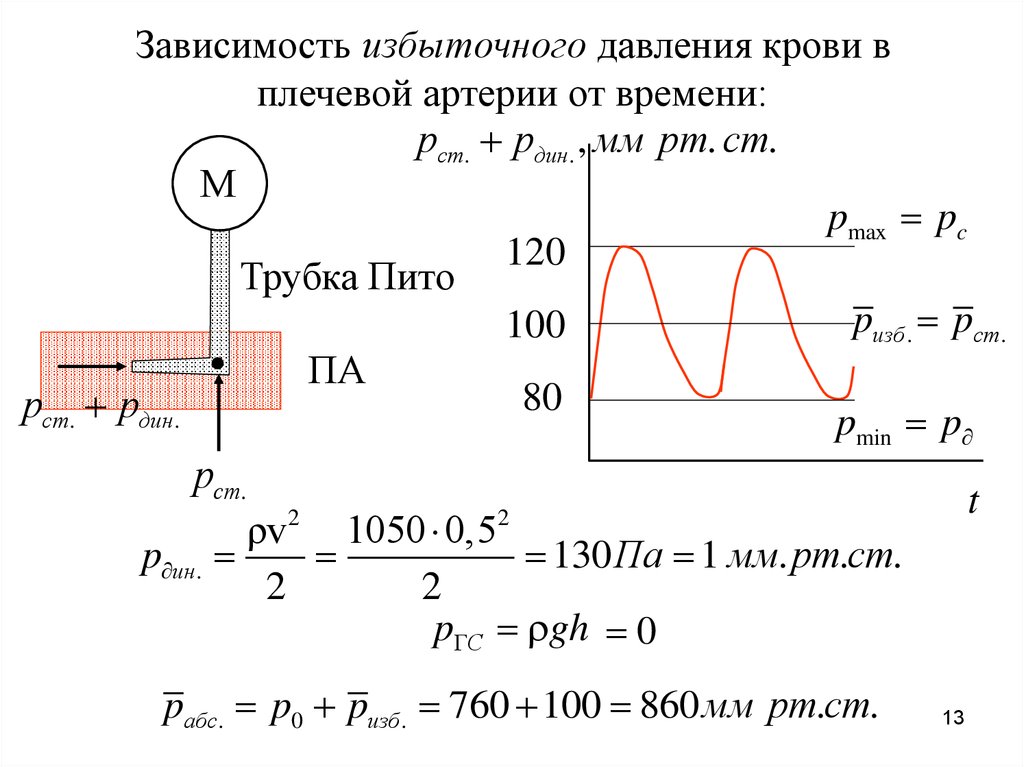
Зависимость избыточного давления крови вплечевой артерии от времени:
рст. рдин. , мм рт. ст.
М
pmax pc
120
Трубка Пито
pизб . pст.
100
ПА
80
рст. рдин.
pmin p
рст.
t
ρv 1050 0,5
p ин.
130 Па 1 мм. рт.ст.
2
2
p С gh 0
2
2
pабс. p0 pизб . 760 100 860 мм рт.ст.
13
14.
МPM PTK PAPT
H 2O
PH
v 0
Н
14
15.
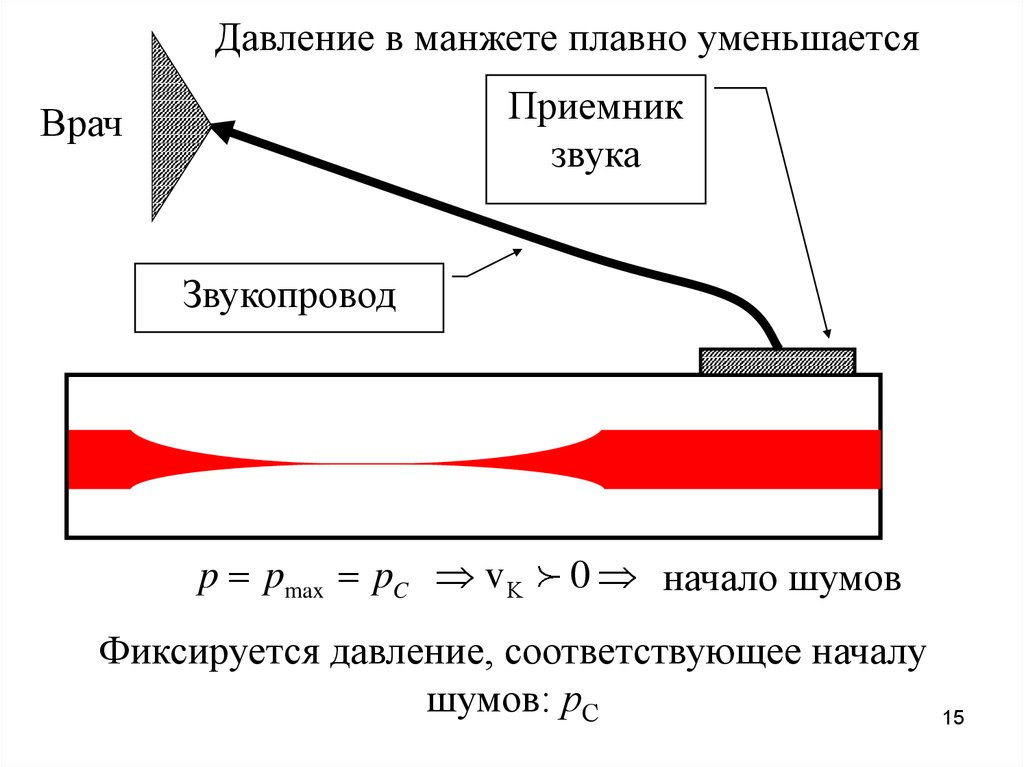
Давление в манжете плавно уменьшаетсяПриемник
звука
Врач
Звукопровод
p pmax pC v
0 начало шумов
Фиксируется давление, соответствующее началу
шумов: рС
15
16.
Давление в манжете плавно уменьшаетсяПриемник
звука
Врач
Звукопровод
p pmin p
прекращение шумов
Фиксируется давление, соответствующее
прекращению шумов: р∂
16
17.
Вода вытекает из сосуда в видепараллелепипеда размерами a x b x c через трубку с
наконечником радиуса r = 1 мм. Уровень наконечника
на l = 1 м ниже нижней грани сосуда. Наконечник
погружен в водоем на глубину h2 = 25 см. Оценить за какое
время вода вытечет из сосуда?
СИ:
l=1м
r = 1 мм =1·10-3 м
a
h2 = 25 см = 0,25 м
а = 2 см = 0,02 м
b = 20 см = 0,2 м
с = 25 см = 0,25 м
c
b
l
H2O
h2
17
18.
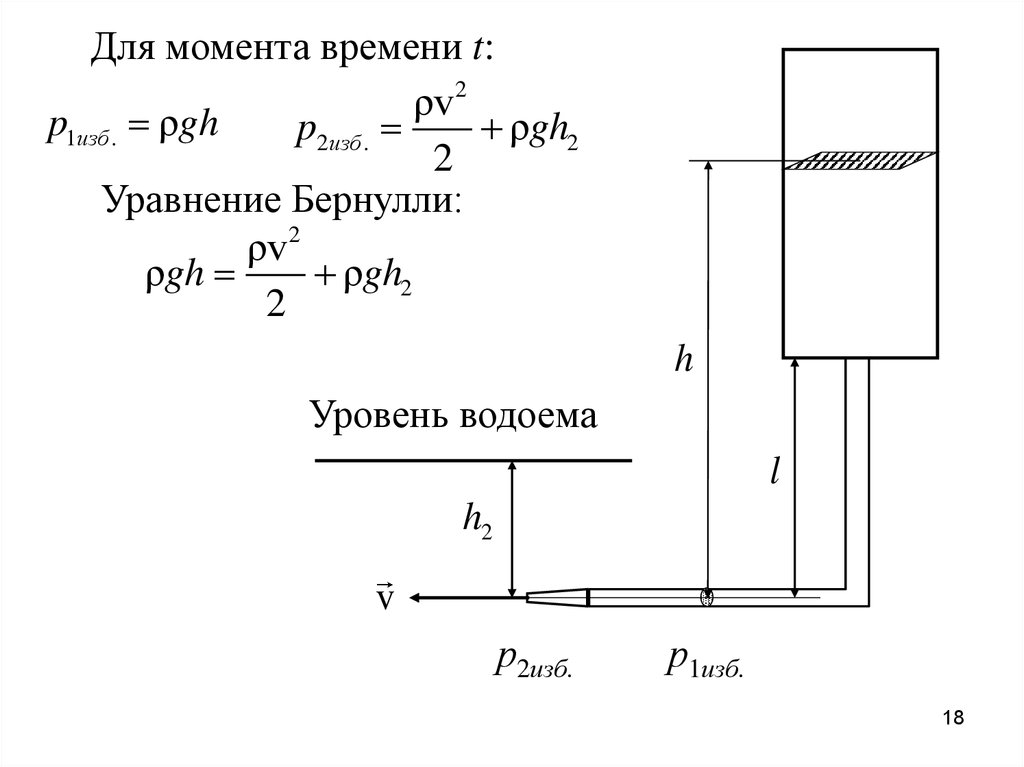
Для момента времени t:ρv 2
p1изб . ρgh
p2изб .
ρgh2
2
Уравнение Бернулли:
ρv 2
ρgh
ρgh2
2
h
Уровень водоема
l
h2
v
р2изб.
р1изб.
18
19.
Скорость вытекания воды из наконечника при уровневоды в сосуде h:
S = a·b
v 2g h h2
dh
За время dt:
1. Из наконечника вытечет
объем воды:
2
dQ v πr dt
2. Уровень воды в сосуде
опустится на dh:
dQ
dh
a b
2 g h h2 πr 2dt
dQ a b dh
2 g h h2 πr dt a b dh
2
19
20.
Разделение переменных:2 g πr 2
dh
dt
a b
h h2
2 g πr
a b
2 g πr 2
t 2
a b
t
t
dh
0
h h2 l
l c
dt h h
l
l c
2a b
2 0,02 0,2
2 t
2
2
l c h2 l h2
l c h2 l h2
2 g πr
2
1 0,25 0,25 1 0,25
10 3,14 10
6
80 с
20
21.
Поверхность жидкости ведет себяподобно пленке из упругого материала,
стремящейся максимально уменьшить
площадь поверхности жидкости
F
p
S
Характеристика поверхностных свойств жидкости –
коэффициент поверхностного натяжения:
F
σ
l
Сила F поверхностного натяжения, действующая на
участок (контур), ограничивающий поверхность
21
жидкости
22.
Масса 110 капель сыворотки крови, вытекающейиз капилляра 1,45 г. Определить коэффициент
поверхностного натяжения сыворотки, если диаметр
шейки капли в момент отрыва 1,00 мм.
СИ:
т = 1,45 г = 1,45·10-3 кг
d = 1,00 мм = 1,00·10-3 м
В момент отрыва капли:
F
N = 100
ρ = 1030 кг/м3
m0 g
m0 g F σl
m
m0 ; l πd
N
mg
σ
πNd
1,45 10 3 9,81
σ
0,0412 Н / м 41,2 мН / м
3
3,14 110 1,00 10
22
23.
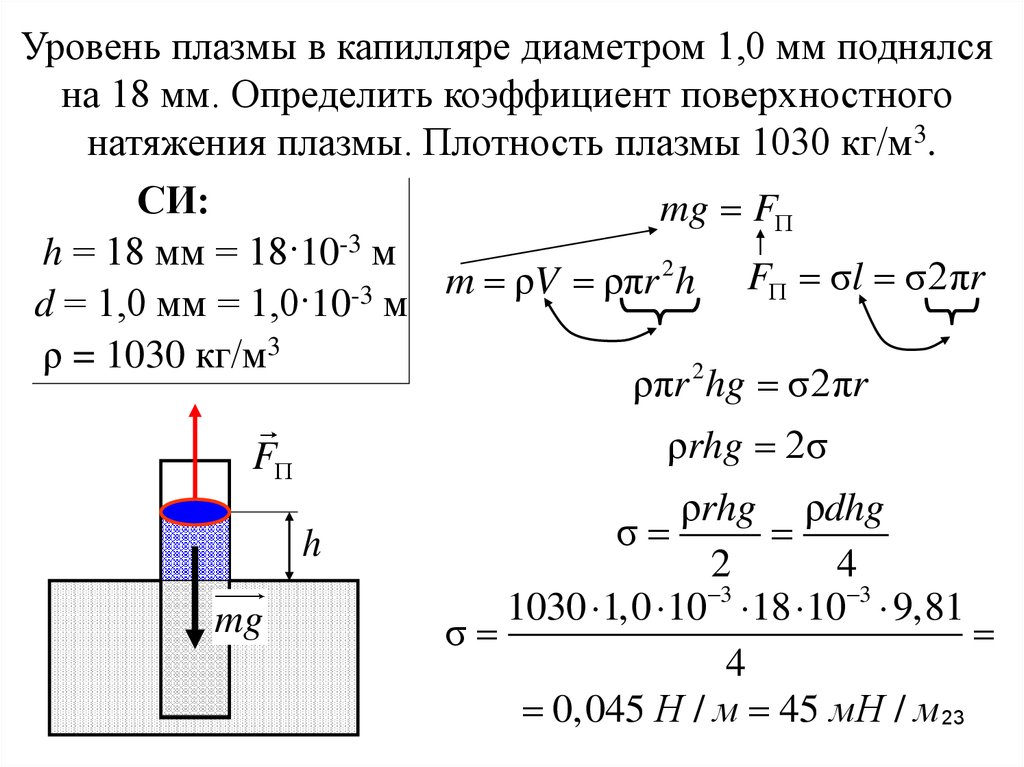
Уровень плазмы в капилляре диаметром 1,0 мм поднялсяна 18 мм. Определить коэффициент поверхностного
натяжения плазмы. Плотность плазмы 1030 кг/м3.
СИ:
mg F
h = 18 мм = 18·10-3 м
2
m
ρ
V
ρπ
r
h F σl σ2πr
-3
d = 1,0 мм = 1,0·10 м
ρ = 1030 кг/м3
ρπr 2 hg σ2πr
ρrhg 2σ
F
h
mg
ρrhg ρdhg
σ
2
4
1030 1,0 10 3 18 10 3 9,81
σ
4
0,045 Н / м 45 мН / м 23
24.
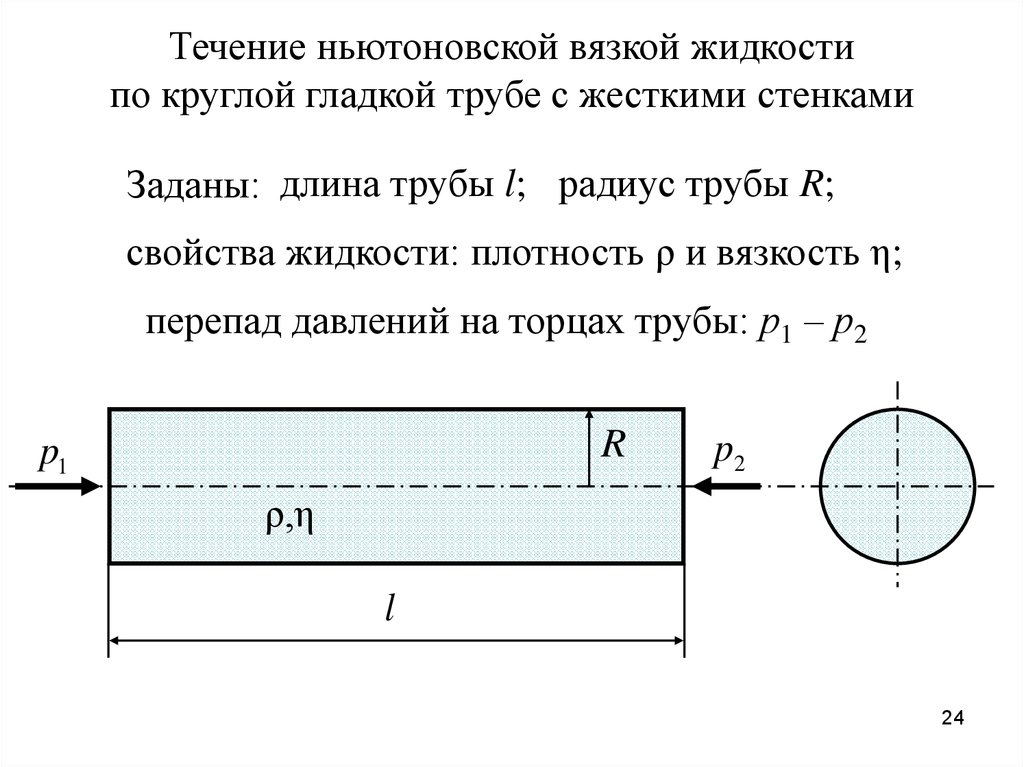
Течение ньютоновской вязкой жидкостипо круглой гладкой трубе с жесткими стенками
Заданы: длина трубы l; радиус трубы R;
свойства жидкости: плотность ρ и вязкость η;
перепад давлений на торцах трубы: р1 – р2
R
p1
p2
ρ,η
l
24
25.
Задачи:1. Описать распределение скоростей частиц жидкости
по сечению трубы
2. Определить расход жидкости через трубу
1.
p1 p2 2 2
v( r )
(R r )
4 l
25
26.
dQ vdS ρv2πr drp1 p2 2 2
v( r )
(R r )
4 l
dr
r
p1 p2 2 2
dQ ρ
( R r )2πr dr
4ηl
R
p1 p2
2
2
Q dQ 2πρ
(
R
r
)r dr
4ηl 0
R
Уравнение Пуазейля:
p1 p2 4
Q πρ
R
8ηl
26
27.
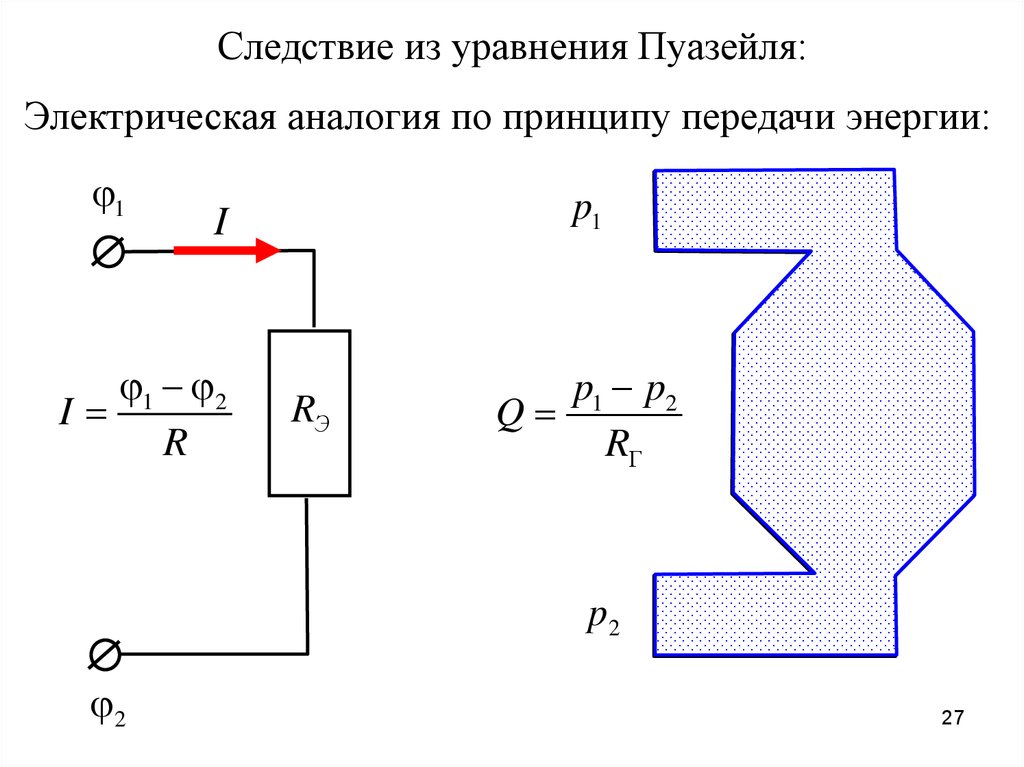
Следствие из уравнения Пуазейля:Электрическая аналогия по принципу передачи энергии:
1
p1
I
1 2
I
R
RЭ
p1 p2
Q
R
p2
2
27
28.
Q Ip1 p2 1 2
1 2
I
RЭ
p1 p2 4
Q π
R
8 l
p1 p2
R
Q
1 2
RЭ
I
8 l
R
4
R
p Па Па с
R кг
кг
Q
с
28
29.
Оцените гидравлическое сопротивление кровеносногососуда длиной 1,2 см и радиусом 1,0 мм.
Коэффициент вязкости крови примите равным 5,0 мПа·с.
Плотность крови 1050 кг/м3.
СИ:
Оценка по Пуазейлю:
l = 1,2 см = 1,2·10-2 м
8 l
-3
R
r = 1,0 мм = 1,0·10 м
4
R
ρ = 1050 кг/м3
3
2
8
5,0
10
1,2
10
-3
η = 5,0 мПа·с = 5,0·10 Па·с R
4
3,14 1050 1,0 10 3
Па с
1,5 10
кг
5
29
30.
При нормальной частоте сокращений сердца полныйкругооборот крови происходит за 60 с.
Считая объём крови равным 5,0 л, определите
общее гидравлическое сопротивление кровотоку.
Перепад давления в сердце принять равным 13,3 кПа.
Плотность крови 1050 кг/м3.
p
p
Q
R
СИ:
R
Q
V 5,0 10 3 м3
m ρV
3
p 13,3 10 a
Q
t
t
t 60c
p t p t
R
m
ρ V
13,3 103 60
5 Па с
R
1,5 10
3
30
кг
1050 5 10
31.
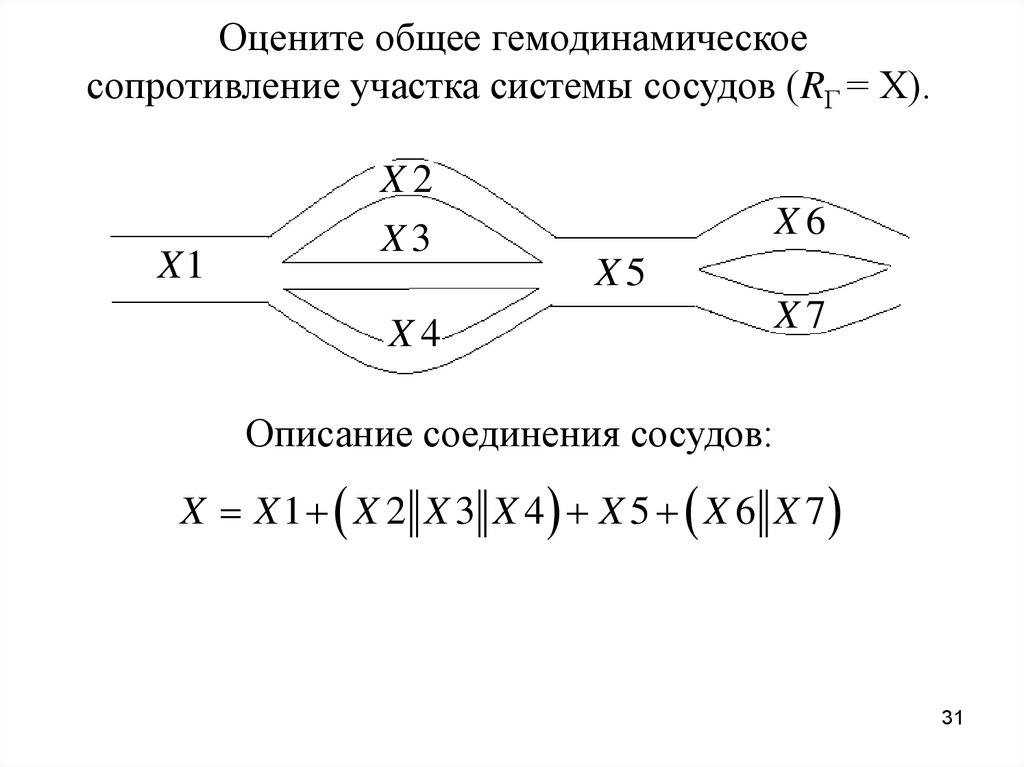
Оцените общее гемодинамическоесопротивление участка системы сосудов (RГ = Х).
X1
X2
X3
X6
X5
X4
X7
Описание соединения сосудов:
X X 1 X 2 X 3 X 4 X 5 X 6 X 7
31
32.
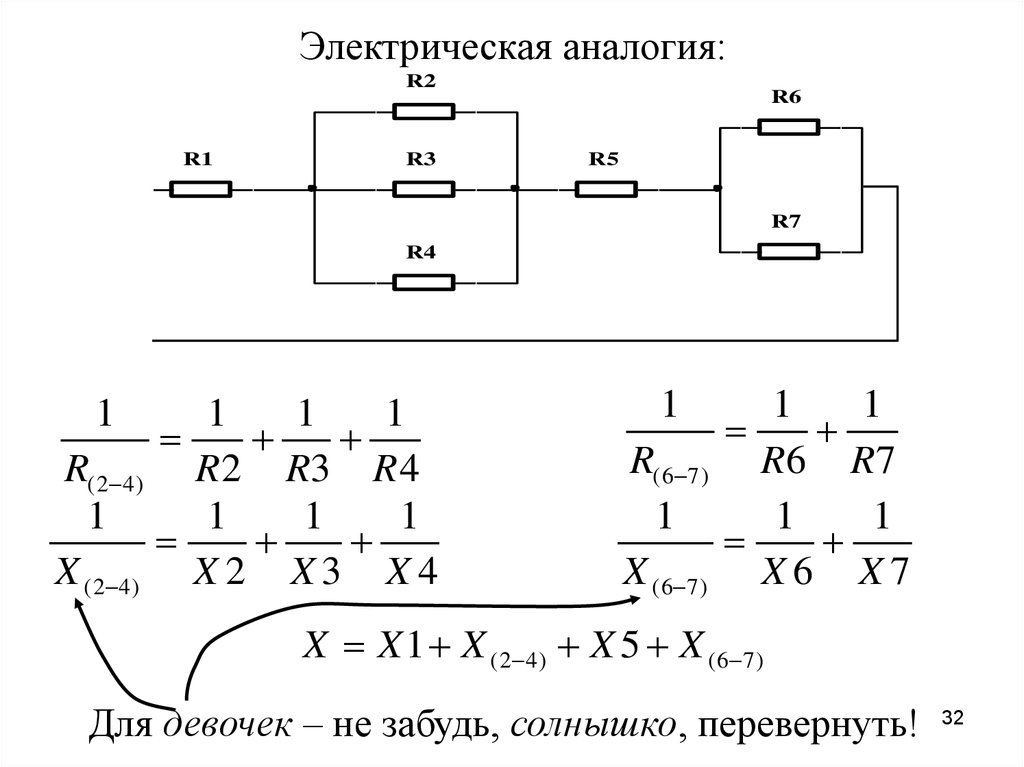
Электрическая аналогия:R2
R1
R3
R6
R5
R7
R4
1
R(2 4)
1
X (2 4)
1
1
1
R 2 R3 R 4
1
1
1
X2 X3 X4
1
R(6 7)
1
X (6 7)
1
1
R6 R7
1
1
X6 X7
X X 1 X (2 4) X 5 X (6 7)
Для девочек – не забудь, солнышко, перевернуть!
32
33.
Казалось бы сложная задача (RГ = Х). :1.Перепад давлений на участке из
пяти сосудов равен 1500 Па.
X 1 1; X 2 2; X 3 4; X 4 6; X 5 1,5
МПа с
X
кг
X2
X1
X3
X5
X4
Определить расходы крови в каждом сосуде:
33
34.
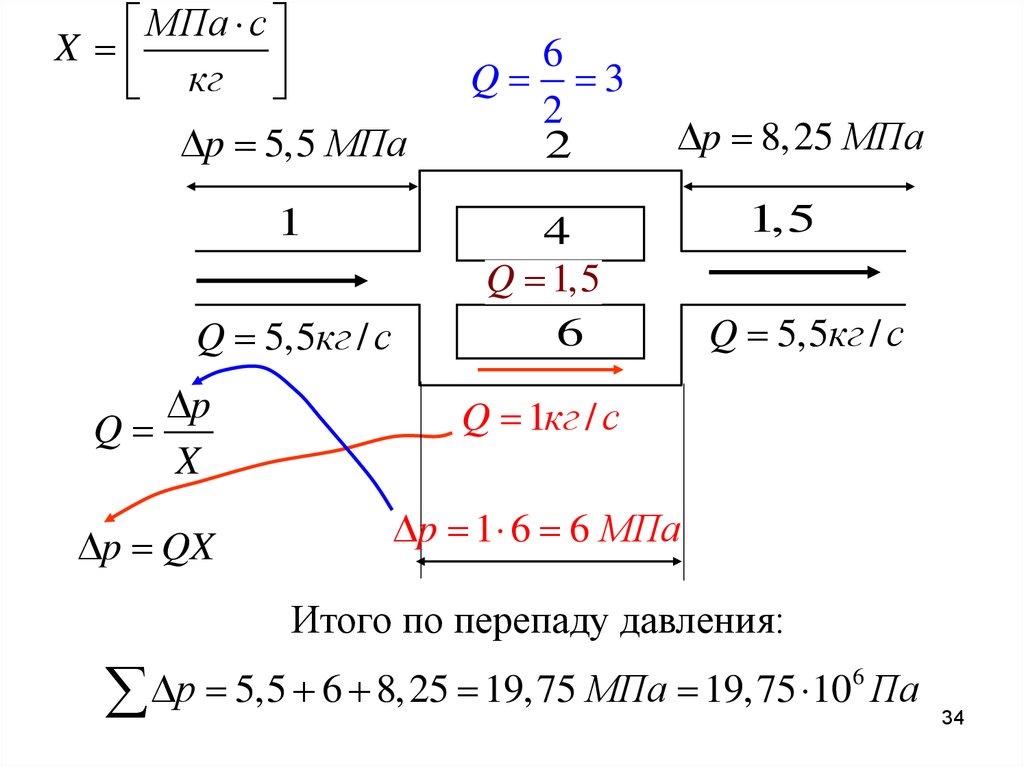
МПа сX
кг
p 5,5 МПа
1
Q 5,5кг / с
6
Q 3
2
2
p 8,25 МПа
4
Q 1,5
6
p
Q
X
Q 1кг / с
p QX
p 1 6 6 МПа
1,5
Q 5,5кг / с
Итого по перепаду давления:
6
р
5,5
6
8,25
19,75
МПа
19,75
10
Па
34
35.
По условию:р 1500 Па
Коэффициент пересчета:
1500
5
k
7,6
10
19,75 106
Все «потолочные» цифры умножаются на коэффициент.
6
Q 3 Q 3 7,6 10 5 23 10 5 кг / с
2
p 1 6 6МПа p 6 106 7,6 10 5 460 Па
35
36.
FFC
m
v
mg
Сила Стокса:
v const
FC v
Для шарика радиуса r:
FC 6πηrv
ρЖ
Определите скорость оседания эритроцитов в плазме
крови (в мм/ч)
исходя из предположения, что они имеют
форму шариков диаметром 7 мкм и не склеиваются
между собой. Вязкость крови 5 мПа·с,
плотность крови 1050 кг/м3,
плотность плазмы крови 1030 кг/м3.
36
37.
FFC
ρ = 1050 кг/м3
mg
Х
Плазма ρП = 1030 кг/м3
v const
Fi mg F FC 0
mg F FC 0
1 3
mg ρVg ρ πd g
6
FC 6πηrv 3πηdv
1 3
F ρ Vg ρ πd g
6
37
38.
61 3
1 3
ρ πd g ρ πd g 3πηdv 0
πd
6
6
ρd 2 g ρ d 2 g 18ηv 0
2
ρ
ρ
d
g
v
18η
м
103 мм
6 мм
3,6 10
v 1
с
час
час
3600
38
39.
При атеросклерозе критическое число Рейнольдса внекоторых сосудах становится равным 1060.
Оцените скорость, при которой возможен
переход ламинарного течения крови в турбулентное
в сосуде диаметром 15 мм.
ρvd
d 15 10 3 м
Re
η
Re η
v
ρ d
η 5 10 3 Па с
ρ = 1050 кг/м3
39
40.
Методы измерения вязкости1. Капиллярный. Основан на уравнении Пуазейля:
определяется время протекания жидкости
заданного объема через капилляр известных
размеров при фиксированном перепаде давления
p1 p2 4
Q πρ
R
8ηl
ρV
p1 p2 4
πρ
R
t
8ηl
p1 p2 4
η π
R t
8lV
40
41.
2. Метод падающего шарика. Основан на измерениискорости равномерного падения шарика известного
радиуса в исследуемой жидкости.
mg F FC 0
FC 6πηrv
3. Ротационный. Основан на измерении вращающего
момента одного из соосных цилиндров при равномерном
вращении его. В пространство между цилиндрами
заливается исследуемая жидкость. Измеряется
не только вязкость, но и зависимость вязкости
от градиента скорости (неньютоновские жидкости).
41
42.
На зачетное занятие«Математика. Механика и гидромеханика»
иметь:
1. Чистая бумага;
2. Авторучки;
3. Калькулятор
Не иметь (даже в мыслях):
1. Полиграфия;
2. Гаджеты
Тема следующего практического занятия:
Электрическое поле и его характеристики.
Поле диполя. Диполь в электрическом поле.
Иметь при себе распечатанные выдачи лекции №4
42































 physics
physics








