Similar presentations:
Особенности молекулярного строения жидкостей. Поверхностные явления. Гидростатика
1.
Лекция 3.Особенности молекулярного строения жидкостей.
Поверхностные явления.
Гидростатика.
Законы гидродинамики.
Вязкость жидкости.
1
2.
Связь с последующей деятельностьюИзучение курса «Биофизика»:
1. Гемодинамика
2. Биофизика дыхания
Практическое применение:
1. Пульмонология
2. Гематология
2
3.
Начальные понятия:Давление силы на поверхность
Fn
S
Fn
p
S
H
p 2 Па
м
Сила давления на
поверхность
независимо от
природы силы:
перпендикулярна
поверхности тела
в любой точке тела
F pS
Действует на тело
«снаружи»
3
4.
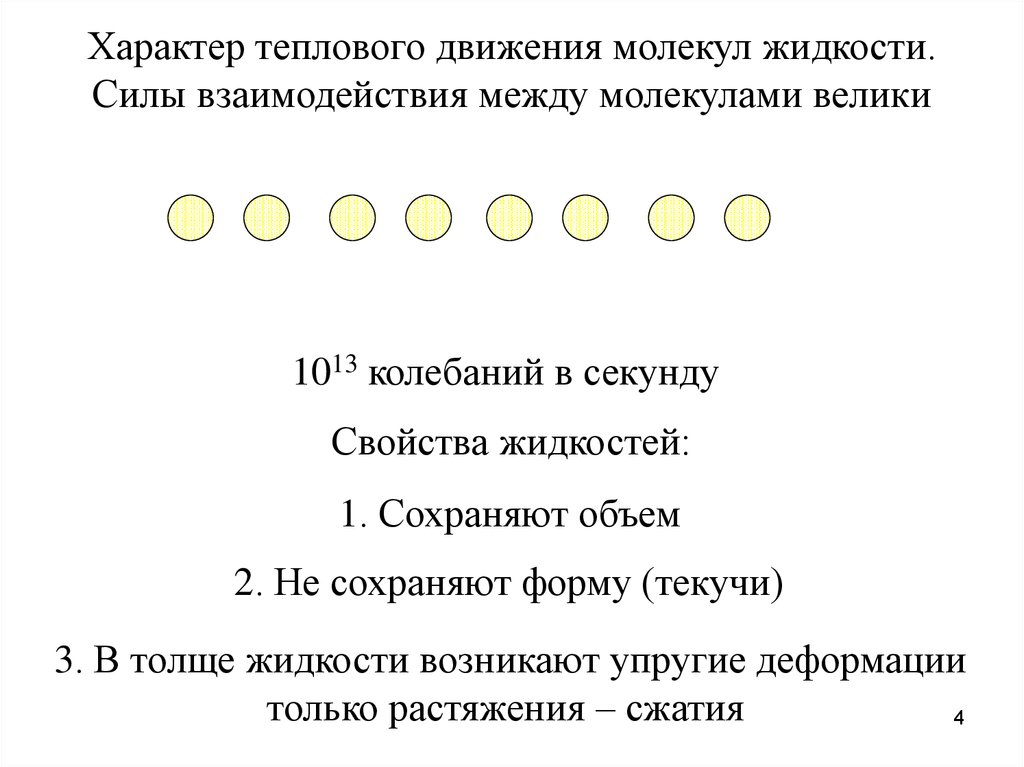
Характер теплового движения молекул жидкости.Жидкости
Силы взаимодействия
между молекулами велики
1013 колебаний в секунду
Свойства жидкостей:
1. Сохраняют объем
2. Не сохраняют форму (текучи)
3. В толще жидкости возникают упругие деформации
только растяжения – сжатия
4
5.
Идеальная жидкость:1. Изотропность всех физических свойств
2. Абсолютная несжимаемость
3. Абсолютная текучесть
(отсутствие сил внутреннего трения)
Гидростатика
Рассматривается жидкость в состоянии покоя
Жидкость считается сплошной средой, состоящей
из частиц с размерами много большими молекулярных
5
6.
Внутри жидкостиСилы, действующие на частицу со
стороны других частиц компенсируют
друга → частица покоится
Поверхностный слой жидкости
Фаза 1 –
пар (газ) n1
n1
n2
Fi1
Граница раздела
Фаза 2 –
жидкость n2
F
Fi 2
F
p
S
6
7.
Поверхность жидкости ведет себяподобно пленке из упругого материала,
стремящейся максимально уменьшить
площадь поверхности жидкости
F
p
S
Характеристика поверхностных свойств жидкости –
коэффициент поверхностного натяжения:
Численно равен работе по изотермическому образованию
единицы поверхности:
A
σ
S
Дж Н
σ 2
м
м
7
8.
Поверхность жидкостиМыльная пленка (Н2О + ПАВ):
Подвижная
перемычка
l
Рамка
F
Мыльная
пленка
F2 2σl
F
σ
l
Сила F поверхностного натяжения, действующая на
участок (контур), ограничивающий поверхность
8
жидкости
9.
Следствия:1. Состояние невесомости → поверхность жидкости –
сфера (минимальная площадь поверхности для данного
объема)
2. Образование капель на конце капилляра при
вытекании из него жидкости:
F
В момент отрыва капли:
mg F σl
Капельный метод определения σ
mg
9
10.
3. Поднятие жидкости в капиллярной трубке:Капилляр с каналом радиуса r
h
Жидкость плотностью ρ,
абсолютно смачивающая
поверхность капилляра
Высота поднятия жидкости:
mg F
2σ
h
ρgr
10
11.
Гидростатическое давление столба жидкости:p С
F
F
p
S
mж g ρ жVg
ρ ж gh
S
S
Следствие:
mж g
S
на тело, погруженное
h в жидкость (газ)
действует суммарная
сила гидростатического
давления (сила Архимеда):
F ρ жVпогр. g
11
12.
Закон ПаскаляДавление, производимое на поверхность жидкости
(газа), передается во все точки жидкости (газа)
без изменения
Абсолютное давление (следствие) складывается
из «внутренних» давлений, обусловленных
свойствами системы (внутренние причины) и внешнего
атмосферного давления (внешняя причина)
pабс. p0 pBH.
Нормальное атмосферное давление:
p0 105 Па 760 мм рт.ст.
12
13.
Суммарное «внутреннее» давление –избыточное над атмосферным.
Измеряется манометром.
pизб . pBH.
Атмосферное давление измеряется барометром
Абсолютное давление:
pабс. p0 pизб .
13
14.
Пример:абсолютное давление
на глубине h в водоеме
p0
Абсолютное давление
(основное уравнение
гидростатики):
pабс. p0 gh
h
«Внутреннее» гидростатическое
давление: p . p С gh
«Внешнее» атмосферное
давление: p0
14
15.
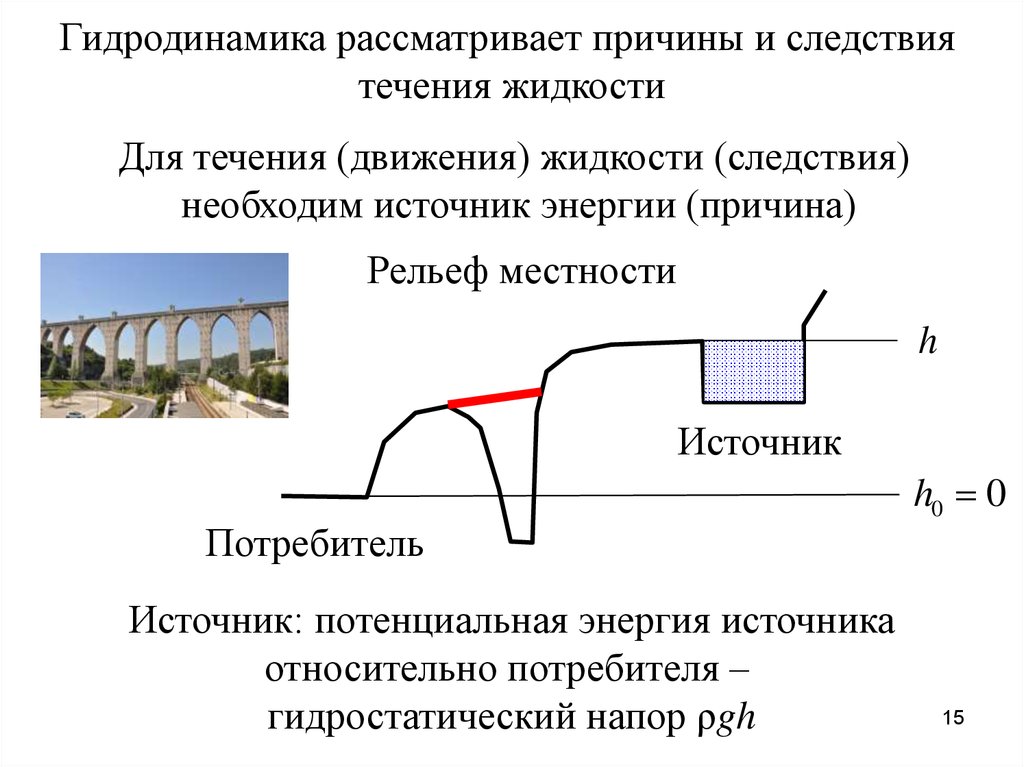
Гидродинамика рассматривает причины и следствиятечения жидкости
Для течения (движения) жидкости (следствия)
необходим источник энергии (причина)
Рельеф местности
h
Источник
Потребитель
Источник: потенциальная энергия источника
относительно потребителя –
гидростатический напор ρgh
h0 0
15
16.
Общая гидродинамическая схемарист.
Источник
энергии
(насос)
рпотр.
Трубопровод
Потребитель
ризб .1
Артериальная часть
ризб .2
Орган 1
Орган 2
Сердце
Венозная часть
Орган i
16
17.
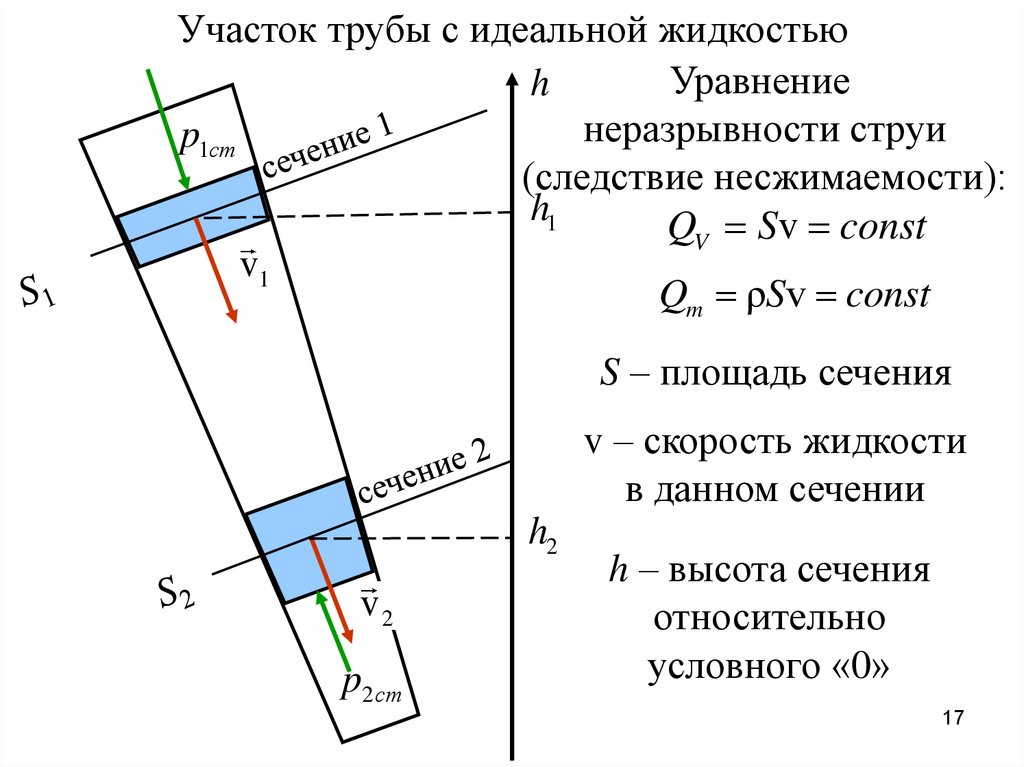
Участок трубы с идеальной жидкостьюУравнение
h
неразрывности струи
p1ст
(следствие несжимаемости):
h1
QV Sv const
v1
Qm ρSv const
S – площадь сечения
v – скорость жидкости
в данном сечении
h2
v2
p2ст
h – высота сечения
относительно
условного «0»
17
18.
Составляющие абсолютного давления:pабс. p0 pизб .
Атмосферное давление:
p01 p02 p0
Составляющие избыточного давления:
1. рст. – статическое давление на выделенное сечение
«снаружи», связанное с работой по
перемещению объема жидкости против сил давления
18
19.
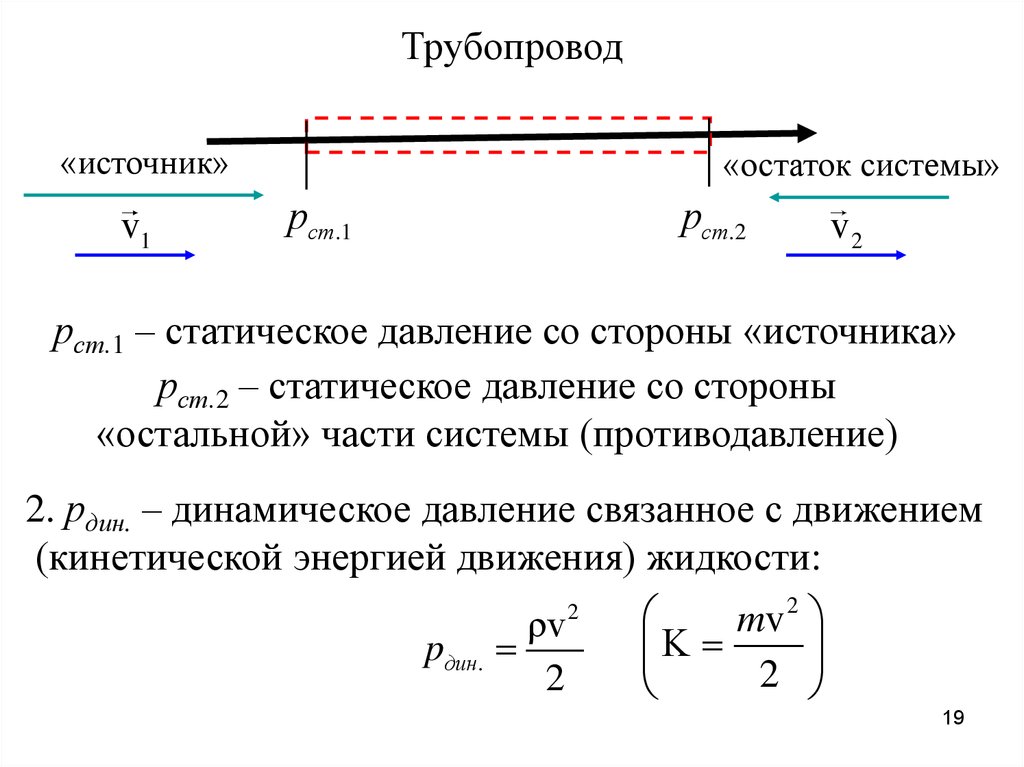
Трубопровод«источник»
v1
«остаток системы»
рст.1
рст.2
v2
рст.1 – статическое давление со стороны «источника»
рст.2 – статическое давление со стороны
«остальной» части системы (противодавление)
2. рдин. – динамическое давление связанное с движением
(кинетической энергией движения) жидкости:
2
2
m
v
ρv
pдин.
2
2
19
20.
3. рГС – гидростатическое давление, связанное сположением сечения относительно условного «0»
(потенциальной энергией положения):
h
p С gh
mgh
Суммарное избыточное давление в данном сечении:
pизб . pBH. рст. рдин. рГС
20
21.
Трубопроводризб .1
Жидкость идеальная →
→ нет потерь давления:
ризб .2
ризб .1 ризб .2 const
Уравнение Бернулли (закон сохранения энергии):
ρv
ρv
pст.1
ρgh1 pст.2
ρgh2 const
2
2
2
1
2
2
21
22.
Реальная жидкость - модель природной жидкости,характеризующаяся изотропностью всех физических
свойств, но в отличие от идеальной модели, обладает
внутренним трением при движении
v const a 0
F
FBH .TP.
Поверхность жидкости
n
a 0 Fi 0
i 1
22
23.
Слой жидкости,движущийся быстрее,
ускоряет более медленно
движущийся слой, и наоборот.
Взаимодействие слоев жидкости, движущихся
с различными скоростями определяет внутреннее трение
z
Характеристика неравномерности
направленного движения слоев –
градиент скорости:
Δz
Δv
v
dv
z
dz
23
24.
Закон Ньютона для вязкого трения:dv
FBH .TP. η
S
dz
η Па с –
коэффициент динамической вязкости
Численно равен силе внутреннего трения,
приходящейся на единичную поверхность
соприкосновения слоев при единичном градиенте
скорости
Коэффициент кинематической вязкости:
η
м2
ν
ν
ρ
с
24
25.
Ньютоновские жидкости:dv
η f
dz
Неньютоновские жидкости:
dv
η f
dz
Сила Стокса
F
v const
FC
m
FC v – сила Стокса
Для шарика радиуса r:
v
mg
ρЖ
FC 6πηrv
F mg F
i
FC 0
25
26.
Течение ньютоновской вязкой жидкостипо круглой гладкой трубе с жесткими стенками
Заданы: длина трубы l; радиус трубы R;
свойства жидкости: плотность ρ и вязкость η;
перепад давлений на торцах трубы: р1 – р2
R
p1
p2
ρ,η
l
26
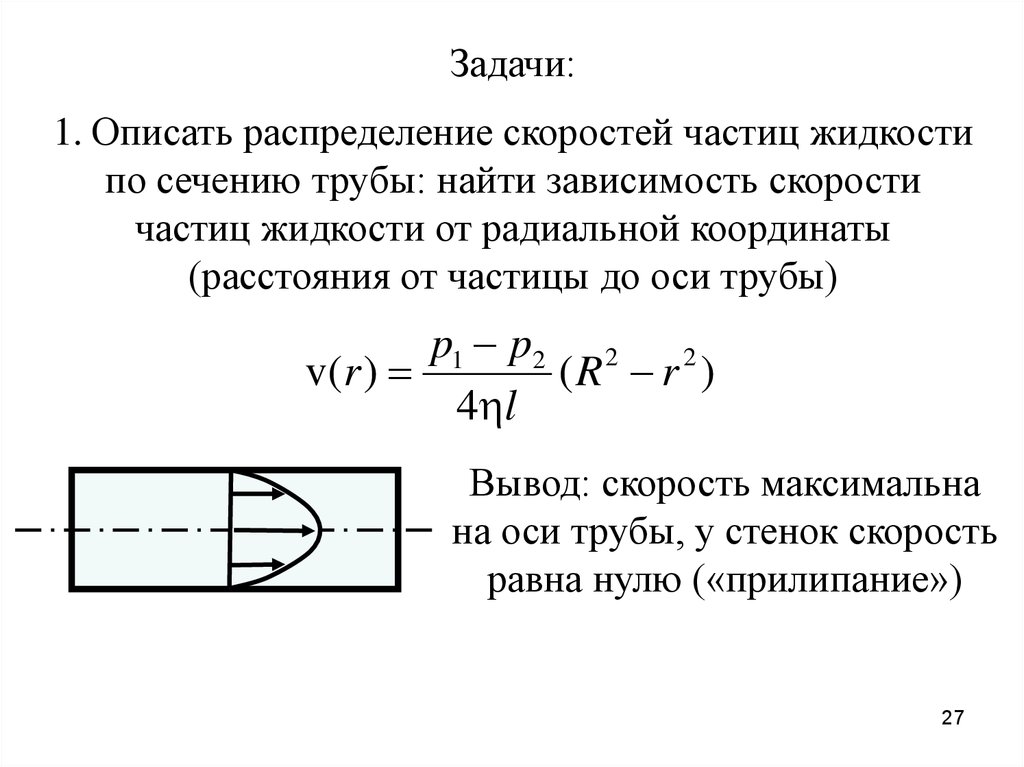
27.
Задачи:1. Описать распределение скоростей частиц жидкости
по сечению трубы: найти зависимость скорости
частиц жидкости от радиальной координаты
(расстояния от частицы до оси трубы)
p1 p2 2 2
v( r )
(R r )
4 l
Вывод: скорость максимальна
на оси трубы, у стенок скорость
равна нулю («прилипание»)
27
28.
2. Определить расход жидкости через трубуСледствие
Уравнение Пуазейля:
Причина
p1 p2 4
Qm πρ
R
8ηl
Общее свойство
жидкости и трубы
p1 p2
Qm
R
Qm I
p1 p2 1 2
1 2
I
R
8 l
R
4
R
RГ – гидравлическое сопротивление трубы
28
29.
Qm1Трубопровод
ризб .1
Qm 2
ризб .2
Qm1 ρ1v1S1 Qm 2 ρ 2 v 2 S2
ризб.1 – давление в сечении 1; ризб.2 – давление в сечении 2
Идеальная жидкость:
ризб .1 ризб .2 const
2
ρv1
pст.1
ρgh1
2
2
ρv 2
pст.2
ρgh2
2
Вязкая жидкость:
ризб .1 ризб .2
Потеря давления на
вязкое трение:
ризб . ризб .1 ризб .2 Qm R
29
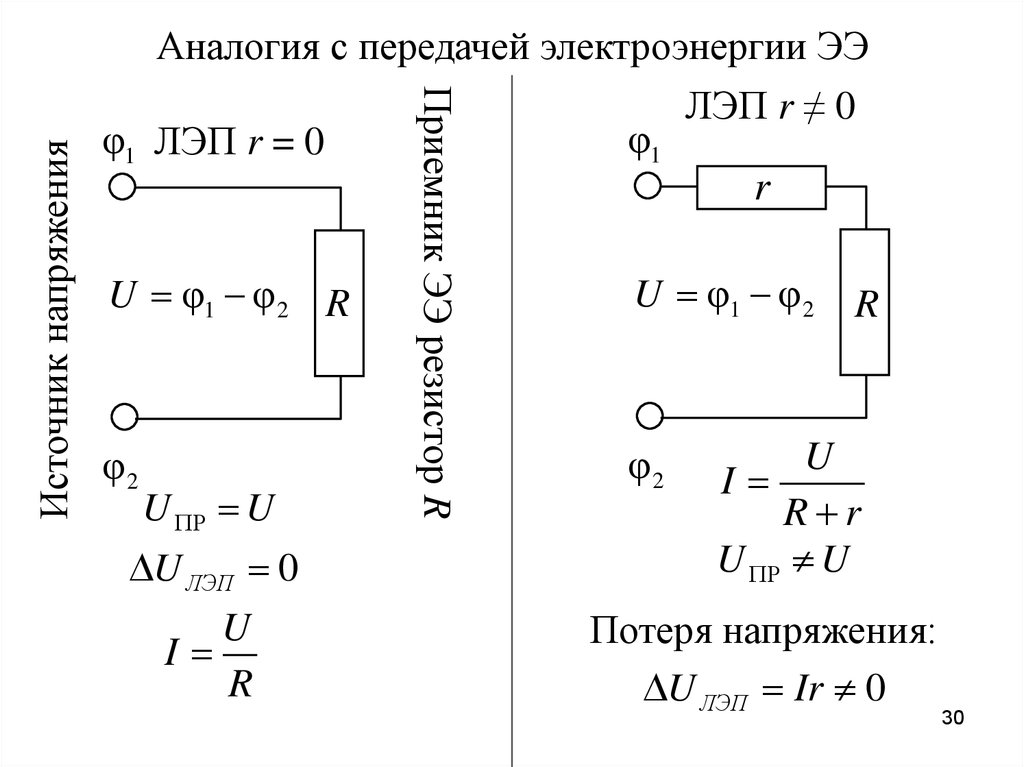
30.
φ1 ЛЭП r = 0U φ1 φ 2 R
φ2
U U
U ЛЭП 0
U
I
R
Приемник ЭЭ резистор R
Источник напряжения
Аналогия с передачей электроэнергии ЭЭ
φ1
ЛЭП r ≠ 0
r
U φ1 φ 2
φ2
R
U
I
R r
U U
Потеря напряжения:
U ЛЭП Ir 0
30
31.
Для произвольных труб (сосудов):8 l – выполняется качественно:
R
4
R
ρ R
η R
R R
l R
p1 p2
Qm
R
R 2
R 1
p1
R 3
R 4
1
R 2,3,4
1
1
1
R 2 R 3 R 4
R 5
p2
R R 1 R 2 R 3 R 4 R 5
31
32.
Ламинарное течение(слоевое)
Траектории отдельных
частиц не пересекаются
Re
Re
Турбулентное течение
(вихревое)
Траектории вихревые,
пересекают друг друга
Re
Re
Характер течения определяется значением критерия
Рейнольдса:
ρvd vd
Re
Re
32
η
33.
Reкритическоекруглые = 2300Re кровикритическое = 970 ± 80
Общие выводы:
1. «Движущей силой» течения любой жидкости
является перепад давления
2. Для любых жидкостей
справедливо уравнение неразрывности
33
34.
3. Уравнение Бернулли для реальных жидкостейимеет качественный (неколичественный) характер:
ρv 22
ρv12
ρgh2
p2 ρgh1
p1
2
2
Причина – потери давления на вязкое трение и на
«геометрию» канала течения
4. Уравнение Пуазейля для реальных жидкостей
имеет качественный (неколичественный) характер:
p1 p2
Q
R f ( , v, l , R)
R
34




























 physics
physics








