Similar presentations:
Физико-математические аспекты нефтегазового дела. Прикладная физика
1.
Программа «Концептуальный инжинирингместорождений нефти и газа»
Курс «Физико-математические аспекты
нефтегазового дела»
Блок «Прикладная физика»
Ганопольский Родион Михайлович, к.ф.-м.н., зав. каф. МФПиС ФТИ
04.09.2017
2.
Прикладная физикаСодержание блока
• Введение
• Свойства жидкостей и газов
• Измерение физических величин
• Гидростатика
• Течение жидкости в трубопроводе
• Высоковязкие жидкости
• Структура многофазного потока
3.
Введение4.
Введение• Основные обозначения
• Системы измерений
• Понятие «гидравлика»
• Терминология
5.
Система обозначенийd— диаметр;
Le— число Льюиса;
М— число Маха;
m —масса жидкости;
Nu— число Нуссельта;
п — показатель степени;
Pr— число Прандтля;
р — давление;
q— скоростной напор;
Re— число Рейнольдса;
Т — температура;
t— время;
и — составляющая вектора скорости в
направлении течения;
η — коэффициент динамической
вязкости;
V — объем жидкости;
ν — коэффициент кинематической
вязкости;
ρ — плотность жидкости или газа;
γ — удельный вес
6.
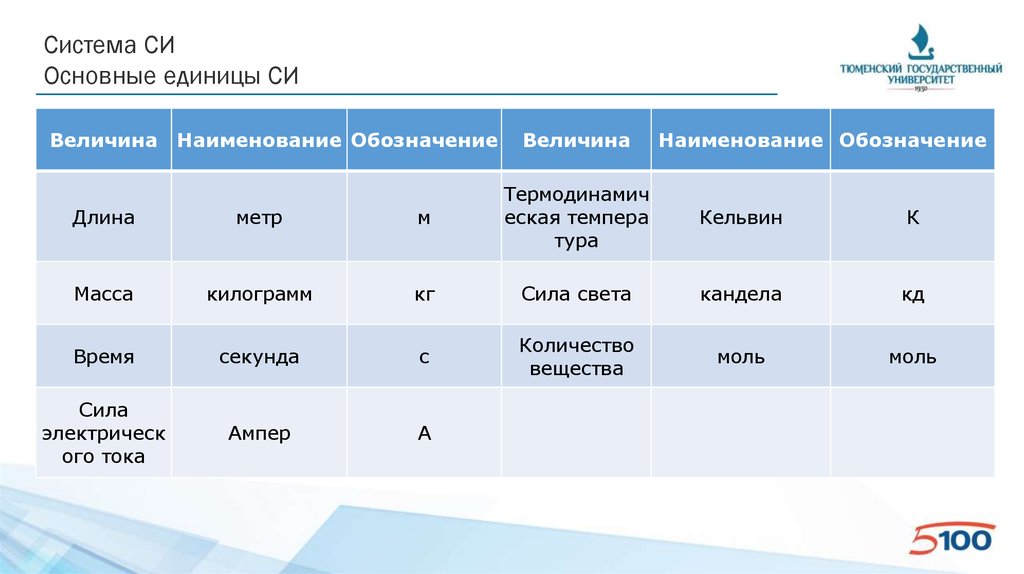
Система СИОсновные единицы СИ
Величина Наименование Обозначение
Величина
Наименование Обозначение
Длина
метр
м
Термодинамич
еская темпера
тура
Масса
килограмм
кг
Сила света
кандела
кд
Время
секунда
с
Количество
вещества
моль
моль
Сила
электрическ
ого тока
Ампер
А
Кельвин
К
7.
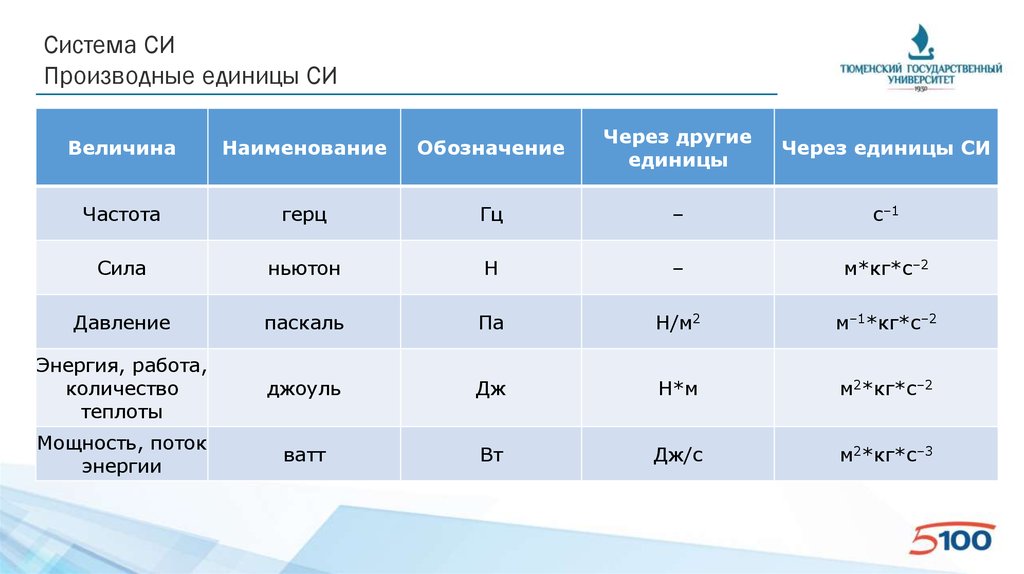
Система СИПроизводные единицы СИ
Величина
Наименование
Обозначение
Через другие
единицы
Через единицы СИ
Частота
герц
Гц
–
с–1
Сила
ньютон
Н
–
м*кг*с–2
Давление
паскаль
Па
Н/м2
м–1*кг*с–2
Энергия, работа,
количество
теплоты
джоуль
Дж
Н*м
м2*кг*с–2
Мощность, поток
энергии
ватт
Вт
Дж/с
м2*кг*с–3
8.
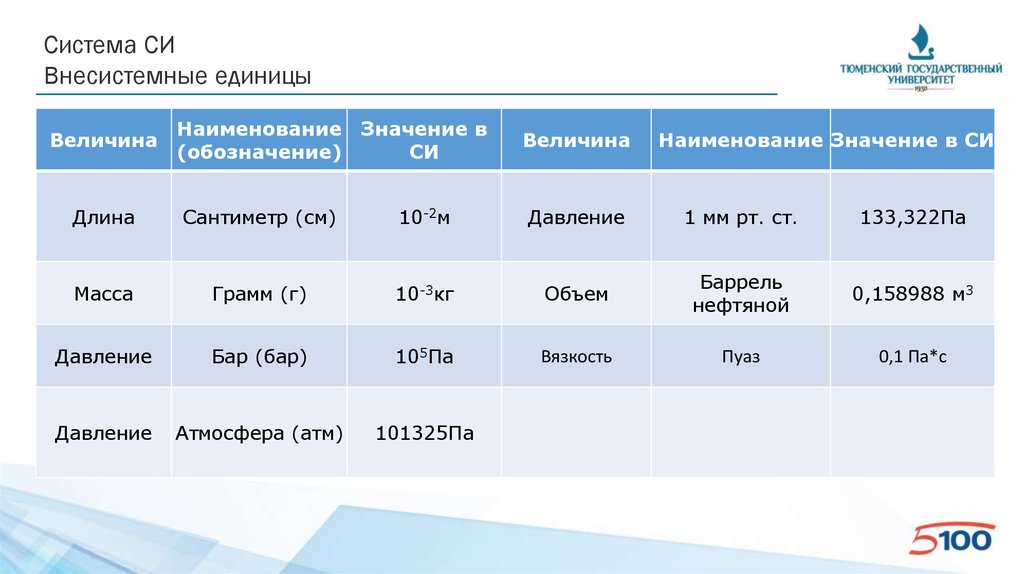
Система СИВнесистемные единицы
Величина
Наименование Значение в
(обозначение)
СИ
Величина
Наименование Значение в СИ
Длина
Сантиметр (см)
10-2м
Давление
1 мм рт. ст.
133,322Па
Масса
Грамм (г)
10-3кг
Объем
Баррель
нефтяной
0,158988 м3
Давление
Бар (бар)
105Па
Вязкость
Пуаз
0,1 Па*с
Давление
Атмосфера (атм)
101325Па
9.
Система СИАнглийская система мер
• Британская имперская система
1 баррель для сырой нефти = 34,97 галлонам = 158,988 л (дм³)
1 тонна большая (длинная) (long ton) = 2240 фунтов = 1016,05 кг
1 морская миля (nautical mile) = 10 кабельтовым = 1,853256 км
1 акр (acre) = 4 рудам = 4046,86 м²
• Американская система мер
1 баррель для сырой нефти = 42,2 галлонов = 158,97 л (дм³)
1 морская миля = 1,852 км
10.
Введение• Гидравлика - прикладная наука о законах движения, равновесии жидкостей и
способах приложения этих законов к решению задач инженерной практики
- физические свойства жидкостей и газов
- гидростатика
- гидродинамика
- кинематическая гидравлика
- примеры практического применения
11.
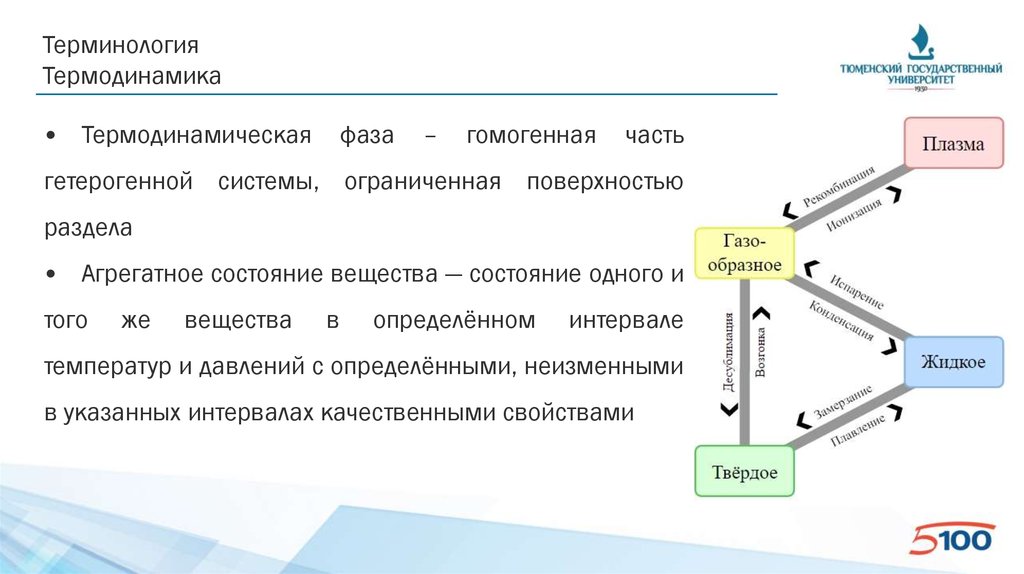
ТерминологияТермодинамика
• Термодинамическая
фаза
–
гомогенная
часть
гетерогенной системы, ограниченная поверхностью
раздела
• Агрегатное состояние вещества — состояние одного и
того
же
вещества
в
определённом
интервале
температур и давлений с определёнными, неизменными
в указанных интервалах качественными свойствами
12.
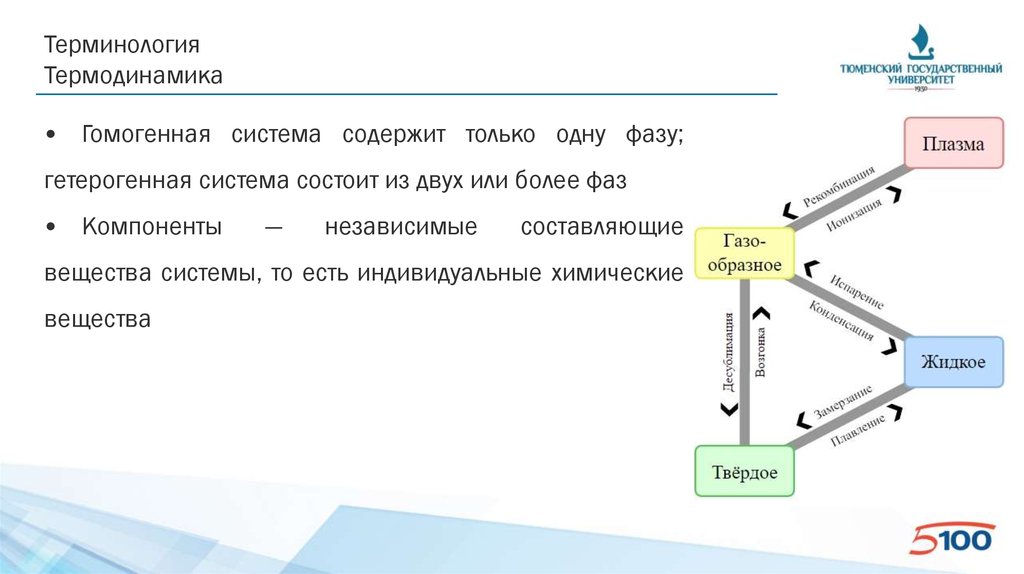
ТерминологияТермодинамика
• Гомогенная система содержит только одну фазу;
гетерогенная система состоит из двух или более фаз
• Компоненты
—
независимые
составляющие
вещества системы, то есть индивидуальные химические
вещества
13.
ТерминологияГидравлика
• Твердое тело – физическое тело со стабильной формой и атомами,
совершающими малые колебания около положения равновесия
• Жидкость – физическое тело, не обладающее способностью сохранять свою
форму из-за слабой связи между отдельными его частицами. Жидкость принимает
форму того сосуда, в котором находится
• Газ – занимает весь предоставленный объем
• К гидромеханике относят жидкие тела и газообразные тела
14.
Свойства жидкостей и газов15.
Свойства жидкостей и газов• Механические свойства жидкостей и газов
- плотность и удельный вес
• Термодинамические свойства
- теплоемкость, температура, давление
• Физические свойства
- упругость, сжимаемость, вязкость, поверхностное натяжение, смачивание,
растворимость
16.
Механические свойства жидкостей• Плотность – отношение массы тела к занимаемому этим телом объему (кг/м3)
• Удельный вес – вес жидкости, приходящийся на единицу объема (Н/м3)
17.
Термодинамические свойства жидкостей и газовТемпература
• Температура – физическая величина, характеризующая термодинамическую
систему и количественно выражающая понятие о различной степени нагретости
тел.
• Обозначение – T (К)
Тс = Т – 273.15К
• 0°С – 273,15К
18.
Термодинамические свойства жидкостей и газовДавление
• Давление — физическая величина, численно равная силе, действующей на
единицу площади поверхности перпендикулярно этой поверхности. В данной точке
давление
определяется
как
отношение
нормальной
составляющей
действующей на малый элемент поверхности, к его площади:
p = ∆F/ ∆S
• Давление газа
силы,
19.
Термодинамические свойства жидкостей и газовУдельная теплоемкость
• Количество теплоты, которое поглощается или выделяется телом при нагреве
или охлаждении пропорционально изменению температуры и массе:
• c – удельная теплоемкость материала
20.
Физические свойства жидкостей и газовСжимаемость
• Сжимаемость – свойство жидкостей и газов изменять свой объем при
изменении
давления,
характеризуется
коэффициентом
объемного
сжатия
(сжимаемости), представляющим относительное изменение объема жидкости при
изменении давления на единицу
21.
Физические свойства жидкостей и газовУпругость
• Упругость – это способность газа принимать свой прежний объем после снятия
внешней нагрузки
E = 1/β
22.
Физические свойства жидкостей и газовВязкость
• Вязкость - свойство жидкости сопротивляться сдвигу или скольжению её слоев.
При
относительном
соприкосновения
перемещении
возникают
силы
слоев
жидкости
сопротивления,
на
поверхности
называемые
их
силами
внутреннего трения, или силами вязкости. Происходит взаимное "торможение" и
"ускорение" соседних слоев
23.
Физические свойства жидкостей и газовВязкость
• Закон Ньютона-Петрова:
τ – сила внутреннего трения слоев жидкости
η – динамический коэффициент вязкости
S – площадь соприкасающихся слоев
∆U – разность скоростей двух соседних слоев жидкости, расположенных на
расстоянии ∆n друг от друга по нормали
24.
Физические свойства жидкостей и газовВязкость
• Динамический коэффициент вязкости
• Кинематическая вязкость - в размерность входят только кинематические
величины
ν=η/ρ
• Ньютоновские жидкости - жидкости, для которых справедлив закон Ньютона
• Неньютоновские жидкости - кефир, сметана, сгущенное молоко, томатные пасты
25.
Физические свойства жидкостей и газовВязкость
• Распределение скоростей при течении вязкой жидкости вдоль стенки
26.
Физические свойства жидкостей и газовВязкость
• Распределение скоростей при течении вязкой жидкости вдоль трубы
27.
Физические свойства жидкостей и газовВязкость
• Распределение скоростей при течении вязкой жидкости вдоль трубы с трением
28.
Физические свойства жидкостей и газовПоверхностное натяжение
29.
Физические свойства жидкостей и газовПоверхностное натяжение
• Система,
находящаяся
в
равновесии,
занимает
положение,
соответствует минимуму энергии
• Силы поверхностного натяжения – силы, направленные по касательной
σ = -R/L
L - длина линии, ограничивающая поверхность раздела.
• Коэффициент поверхностного натяжения
• Дополнительное давление (формула Лапласа)
ρ=σ/(1/R1+1/R2)
которое
30.
Физические свойства жидкостей и газовПоверхностное натяжение. Проявления
• В невесомости капля принимает сферическую форму
• Струя воды «сливается» в цилиндр, который затем разбивается на шаровидные
капли
• Маленькие объекты с плотностью, большей плотности жидкости, способны
«плавать» на поверхности жидкости
31.
Физические свойства жидкостей и газовСмачивание. Угол смачивания
• Смачивание — физическое взаимодействие жидкости с поверхностью твёрдого
тела или другой жидкости
• Полное несмачивание
• Частичное несмачивание
• Частичное смачивание
• Полное смачивание
32.
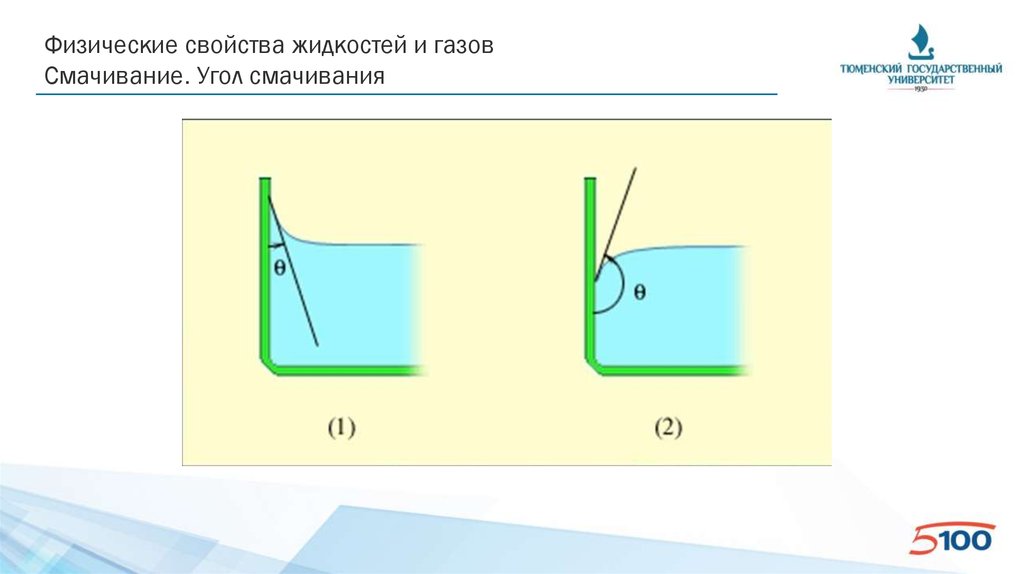
Физические свойства жидкостей и газовСмачивание. Угол смачивания
• Смачивание зависит от соотношения между силами
сцепления молекул жидкости с молекулами (или атомами) смачиваемого тела
(адгезия) и силами взаимного сцепления молекул жидкости (когезия).
• Молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам
твёрдого тела – несмачивание
• Молекулы жидкости притягиваются друг к другу слабее, чем к молекулам
твёрдого тела – смачивание
33.
Физические свойства жидкостей и газовСмачивание. Угол смачивания
34.
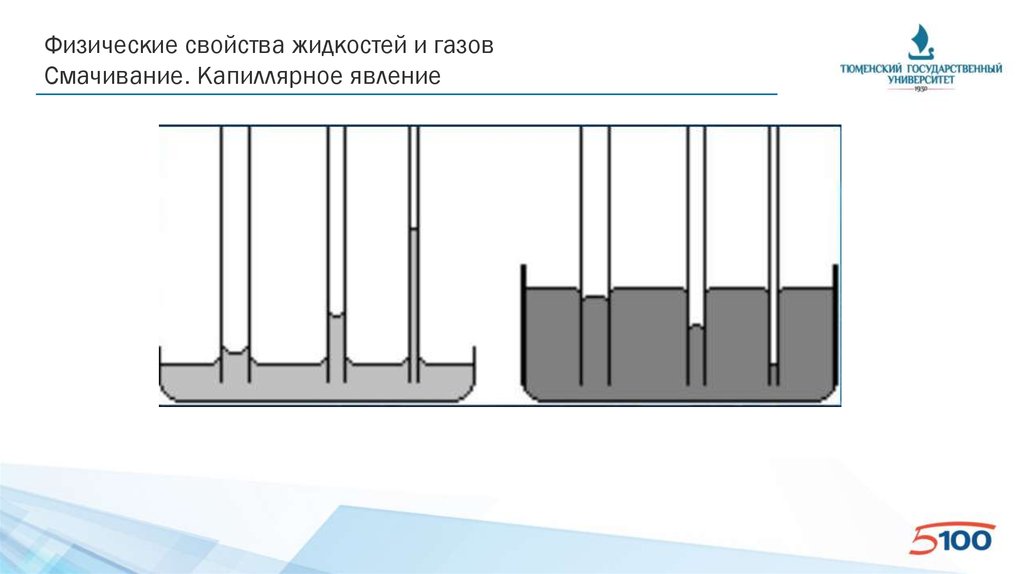
Физические свойства жидкостей и газовСмачивание. Капиллярное явление
35.
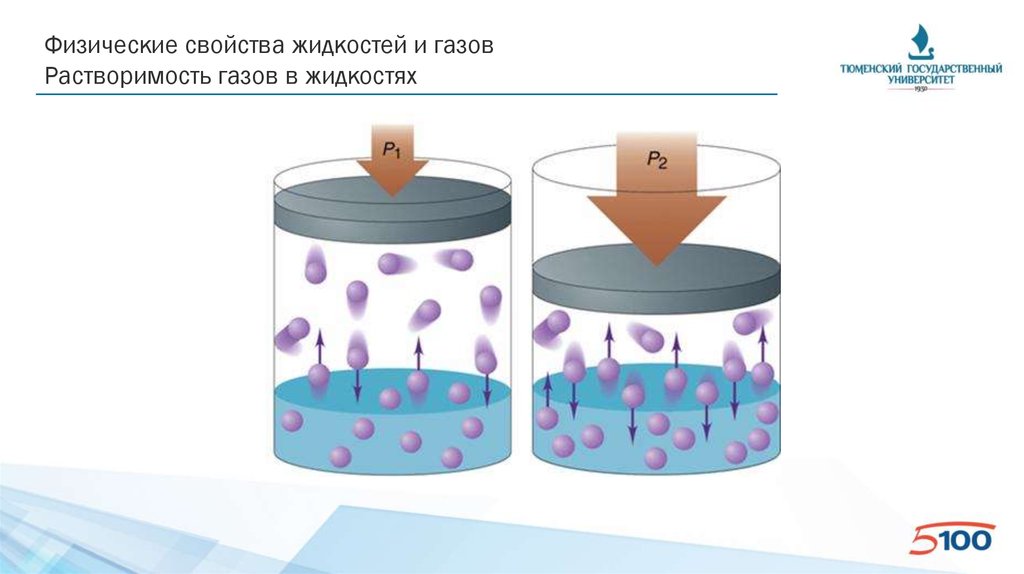
Физические свойства жидкостей и газовРастворимость газов в жидкостях
• Растворимость газа в жидкости – количество растворенного газа в единице
объема жидкости
• Закон Генри: растворимость газа пропорциональна его давлению
• При понижении давления выделяется растворенный в жидкости газ, причем
интенсивнее, чем растворяется в ней. Выделиться газ может в считанные
секунды или даже доли секунды
36.
Физические свойства жидкостей и газовРастворимость газов в жидкостях
37.
Физические свойства жидкостей и газовИспаряемость
• Испаряемость – свойство капельных жидкостей превращаться в пар
• Интенсивное парообразование по всему объему — кипение жидкости
• Свойство имеет как положительные, так и отрицательные стороны
- Положительное - это возможность из нефти получать различные фракции и
множество нефтепродуктов и сырья для химической промышленности;
способность полного сгорания нефтепродуктов в ДВС, турбинах, котельных
установок
- Отрицательное - теряется большое количество нефти (до 10—12% в год от
объема добычи)
38.
Физические свойства жидкостей и газовКавитация
• Кавитация – местное нарушение сплошности течения жидкости с образованием
паровых и газовых пузырей
• Процесс парообразования и последующего схлопывания пузырьков пара с
одновременным конденсированием пара в потоке жидкости
39.
Физические свойства жидкостей и газовКавитация
40.
Идеальная и реальные жидкости• Идеальная жидкость – это абсолютно несжимаемая, абсолютно невязкая и
абсолютно нетеплопроводная жидкость. В природе таких жидкостей не существует
• Реальные жидкости обладают сжимаемостью, вязкостью и теплопроводностью,
однако решение ряда теоретических вопросов в гидравлике значительно
облегчается при использовании идеальной жидкости
41.
Измерение физических величин42.
Измерение физических величинМетоды
• Непосредственно прибором
• Расчетные – с помощью формул на основании измеренных других величин
43.
Приборы для измерения физических величинПриборы
• Термометр - температура
• Барометр и манометр – давление
• Весы – масса
• Динамометр – сила
• Психрометр – относительная влажность воздуха
• Вискозиметр – вязкость
• Ареометр – плотность жидкостей
• Расходомер – расход вещества
44.
Приборы для измерения физических величинТермометры
• жидкостные
• механические
• электронные
• оптические
• инфракрасные
• газовые
45.
Приборы для измерения физических величинТермометры
• жидкостные: основаны на принципе изменения объёма жидкости, которая
залита в термометр, при изменении температуры окружающей среды
• механические: действуют по тому же принципу, что и жидкостные, но в качестве
датчика обычно используется металлическая спираль или лента из биметалла
• электронные: принцип основан на изменении сопротивления проводника при
изменении температуры окружающей среды
46.
Приборы для измерения физических величинТермометры
• оптические:
позволяют
регистрировать
температуру
благодаря
изменению уровня светимости, спектра и иных параметров при изменении
температуры (частный случай инфракрасные термометры)
• газовые: основаны на законе Шарля (p~T при V=const)
47.
Приборы для измерения физических величинБарометры
• Барометр — прибор для измерения атмосферного давления
• Барометры делятся на жидкостные и механические
- в жидкостных барометрах давление измеряется высотой столба жидкости
- крышка коробочки, к которой прикреплена пружина с передающим механизмом,
деформируется, из-за чего стрелка на шкале показывает соответствующие данные
48.
Приборы для измерения физических величинМанометры
• Манометр — прибор, измеряющий давление жидкости или газа
• Манометр делятся на жидкостные, грузопоршневые, деформационные (с
трубчатой пружиной или мембраной)
• Механическое
измерение
давления
основывается
на
эластичном
измерительном элементе, способном под воздействием сжимающей нагрузки
деформироваться строго определенным образом и испытанную деформацию
воспроизводить
49.
Приборы для измерения физических величинВесы и динамометр
• Механические динамометры (рычажные и пружинные), а также гидравлические
и электрические
• Два вида механических динамометров: пружинный и рычажный
• Действие гидравлического динамометра основано на вымещении измеряемой
силой жидкости из цилиндра
• Электрический
динамометр
состоит
из
датчика,
деформацию от воздействия силы в электрический сигнал
который
преобразует
50.
Приборы для измерения физических величинВискозиметры
• Капиллярные
• Ротационные
• С падающим шариком
• Пузырькового типа
• Ультразвуковые
51.
Приборы для измерения физических величинВискозиметры
• Капиллярные: основаны на подсчёте времени протекания заданного объёма
жидкости через узкое отверстие или трубку при заданной разнице давлений
• Ротационные: два тела вращения, одинаковых или разных, совмещаются
по осям так, что одно из них прикасается изнутри к другому. Пространство между
телами заполняют исследуемым веществом, и к одному из тел подаётся крутящий
момент
52.
Приборы для измерения физических величинВискозиметры
• С падающим шариком: определяется по времени прохождения шариком
некоего расстояния под воздействием его собственного веса
• Пузырькового типа: основан на определении параметров движения пузырька
газа, свободно всплывающего в вязкой среде
• Ультразвуковые: изменение резонансной частоты колебаний в жидкости
различной вязкости
53.
Приборы для измерения физических величинАреометр
• Основан на законе Архимеда
• Плотность жидкостей сильно зависит от температуры, измерения концентрации
должны проводиться при строго определенной температуре, для чего ареометр
иногда снабжают термометром
• Для
практического
применения
ареометр
растворенного вещества, например, спиртомер
градуируют
в
концентрации
54.
Приборы для измерения физических величинРасходомер
• Расходомер — прибор, измеряющий количество вещества (объем, масса),
проходящее через данное сечение потока в единицу времени
• Делятся на:
- использующие гидродинамические методы
- с непрерывно движущимся телом
- основанные на различных физических явлениях
- основанные на особых методах
55.
Приборы для измерения физических величинРасходомеры, использующие гидродинамические методы
• Парциальные расходомеры
• Расходомеры переменного давления
• Расходомер переменного уровня
• Расходомеры обтекания
• Вихревые расходомеры
56.
Приборы для измерения физических величинРасходомеры, использующие гидродинамические методы
• Расходомеры переменного давления: измеряют расход по перепаду давления,
который создается в трубопроводе сужающим устройством, установленным внутри
трубопровода
• Расходомер переменного уровня: в основе работы лежит зависимость между
расходом жидкости и высотой ее уровня в сосуде, при этом жидкость должна
постоянно поступать в сосуд и вытекать через небольшое отверстие
• Расходомеры обтекания: чувствительный элемент воспринимает динамическое
давление потока и перемещается под его воздействием
57.
Приборы для измерения физических величинРасходомеры, использующие гидродинамические методы
• Вихревые расходомеры:
расход зависит от частоты колебания давления.
Колебания давления возникают в потоке в процессе вихреобразования или
колебания струи либо после препятствия определенной формы, установленного в
трубопроводе, либо специального закручивания потока
• Парциальные расходомеры: расход вещества определяется через некоторую
долю основного потока в небольшой трубе, подключенной параллельно
основному трубопроводу
к
58.
Приборы для измерения физических величинРасходомеры с непрерывно движущимся телом
• Камерные счетчики и расходомеры: отмеривают с помощью камеры
одинаковые порции. Расход – количество порций.
• Силовые расходомеры: основанные на зависимости от массового расхода
эффекта силового воздействия, сообщающего потоку ускорение того или другого
рода (какая сила или мощность требуются)
• Тахометрические-расходомеры: имеют подвижный, обычно вращающийся
элемент, скорость движения которого пропорциональна объемному расходу
59.
Приборы для измерения физических величинРасходомеры, основанные на различных физических явлениях
• Акустические расходомеры
• Ионизационные расходомеры
• Оптические расходомеры
• Тепловые расходомеры
• Электромагнитные расходомеры
• Ядерно-магнитные расходомеры
60.
Приборы для измерения физических величинРасходомеры, основанные на особых методах
• Концентрационные расходомеры
• Корреляционные расходомеры
• Меточные расходомеры
• Расходомеры с автоколеблющимся телом
• Расходомеры с подвижным участком трубопровода
• Струйные расходомеры
61.
Расчётные методы измерения физических величинПример 1
• Сосуд заполнен водой, занимающей объем V1=2м³. При увеличении давления
на величину 200 бар при температуре 20°С объем воды уменьшился до 1,981 м³?
Найти модуль упругости для воды при данной темпертуре.
62.
Расчётные методы измерения физических величинПример 1. Решение
• Изменение объема
∆V = V2 - V1 = -0,019 м³
• Увеличение давления ∆p=200 бар=2*107 Па
• Коэффициент объемного сжатия
β = ∆V/V/∆p = 4,74*10-10 1/Па
• Модуль объемной упругости
E = 1/β = 2,11*109 Па
63.
Расчётные методы измерения физических величинПример 2
• Определить коэффициент динамической и кинематической вязкости воды, если
шарик d = 2 мм из эбонита с ρ = 1,2*103 кг/м3 падает в воде с постоянной
скоростью u = 0,33 м/с. Плотность воды ρ = 103 кг/м3 .
64.
Расчётные методы измерения физических величинПример 2. Решение
• Сила сопротивления определяется по формуле Стокса
F = 3*π*μ*u*d
• Вес шарика
G = ρ*g*π*d3/6
• Скорость постоянна, значит, F = G
3*π*μ*u*d = ρ*g*π*d3/6
μ = ρ*g*d2/18/u = 0,008 Па*с
• Коэффициент кинематической вязкости
ν=μ/ρ=8*10-6м2/с
65.
Гидростатика66.
Гидростатика• Гидростатическое давление
• Основное уравнение гидростатики
• Давление на стенки сосуда
• Законы Паскаля и Архимеда
• Примеры расчётов
67.
Гидростатика• На жидкость, находящуюся в состоянии покоя, действуют силы, которые можно
разделить на поверхностные и массовые
• Поверхностные силы приложены к частицам жидкости, находящимся на
поверхности раздела данной жидкости и другой среды
• Массовые силы воздействуют на все частицы данного объема жидкости и
пропорциональны массе каждой частицы
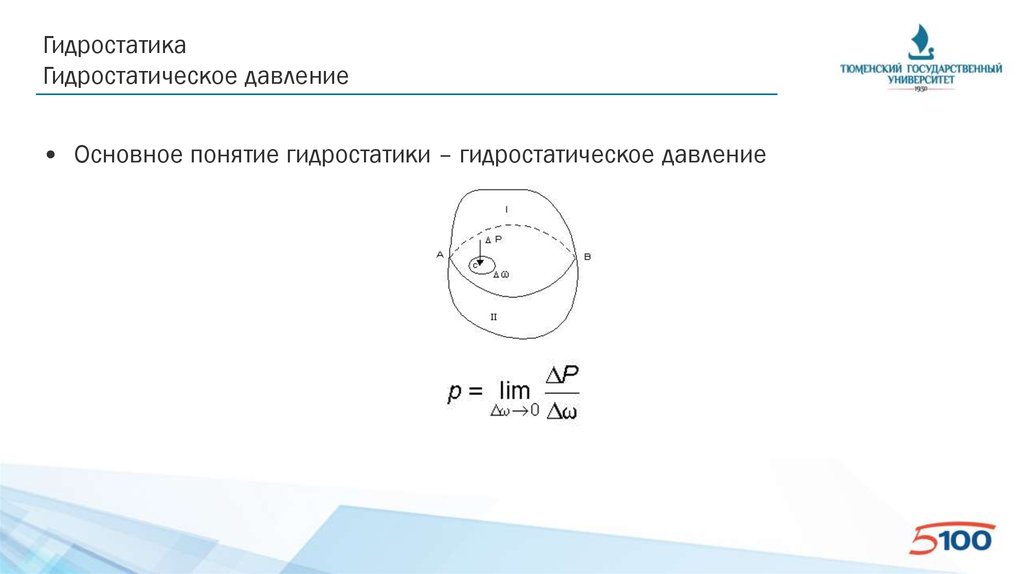
• Основное понятие гидростатики – гидростатическое давление
68.
ГидростатикаГидростатическое давление
• Основное понятие гидростатики – гидростатическое давление
69.
ГидростатикаГидростатическое давление
• Гидростатическое давление направлено всегда по внутренней нормали к
площадке, на которой это давление действует и является сжимающим
напряжением, потому что в покоящейся жидкости не могут существовать
касательные и растягивающие усилия
• Величина гидростатического давления в любой точке жидкости по всем
направлениям одинакова
• Различают давление абсолютное (полное) и избыточное
70.
ГидростатикаОсновное уравнение гидростатики
• X, Y, Z – проекции единичных массовых сил на соответствующие координатные
оси
71.
ГидростатикаПоверхность уровня
• Поверхность уровня – поверхность равного давления
• Две поверхности уровня не пересекаются между собой
• Массовые силы направлены нормально к поверхности уровня
• Поверхность уровня на границе жидкой и газообразной среды называется
свободной поверхностью
72.
ГидростатикаДавление при абсолютном покое
• В состоянии абсолютного покоя под действием сил тяжести и внешнего
давления на свободной поверхности
X = 0; Y = 0; Z = -g
dp = -ρ*g*dz
p = p0 + ρ*g*h
• Основное уравнение гидростатики
• Поверхность уровня (и свободная поверхность) при абсолютном покое –
горизонтальная плоскость
z = const
73.
ГидростатикаАнализ основного уравнения гидростатики
• Гидростатическое давление p есть сумма внешнего давления p0, действующего
на свободной поверхности и весового давления ρ*g*h, создаваемого весом
столба жидкости высотой h
• Внешнее давление передается во все точки покоящейся жидкости без
изменения, поэтому жидкость используется как среда для передачи давления
(гидравлические машины) – закон Паскаля
• Поверхность уровня (и свободная поверхность) при абсолютном покое –
горизонтальная плоскость
z = const
74.
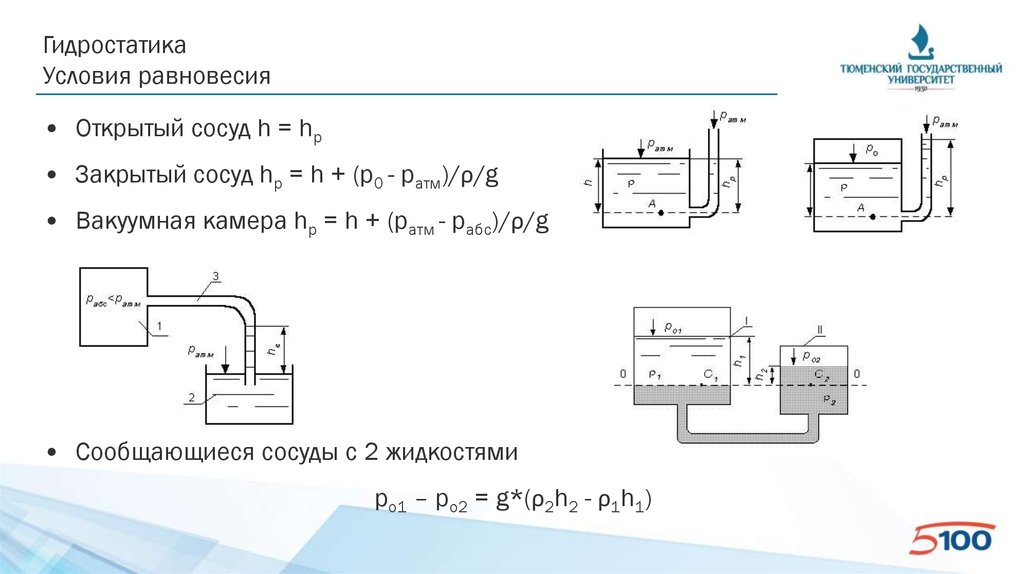
ГидростатикаУсловия равновесия
• Открытый сосуд h = hp
• Закрытый сосуд hp = h + (p0 - pатм)/ρ/g
• Вакуумная камера hp = h + (pатм - pабс)/ρ/g
• Сообщающиеся сосуды с 2 жидкостями
po1 – po2 = g*(ρ2h2 - ρ1h1)
75.
ГидростатикаСообщающиеся сосуды с 2 жидкостями
• В сосудах налита одинаковая жидкость, но давления различны
po1 – po2 = g*ρ*(h2 - h1)
• В сосудах налита одинаковая жидкость и давления одинаковы (принцип
сообщающихся сосудов)
h1 = h2
• Жидкость одинакова, но один сосуд открыт, а другой закрыт
hp = h + (pатм - pабс)/ρ/g
• Жидкости разнородные, несмешивающиеся, а давления сопадают
ρ2h2 = ρ1h1
76.
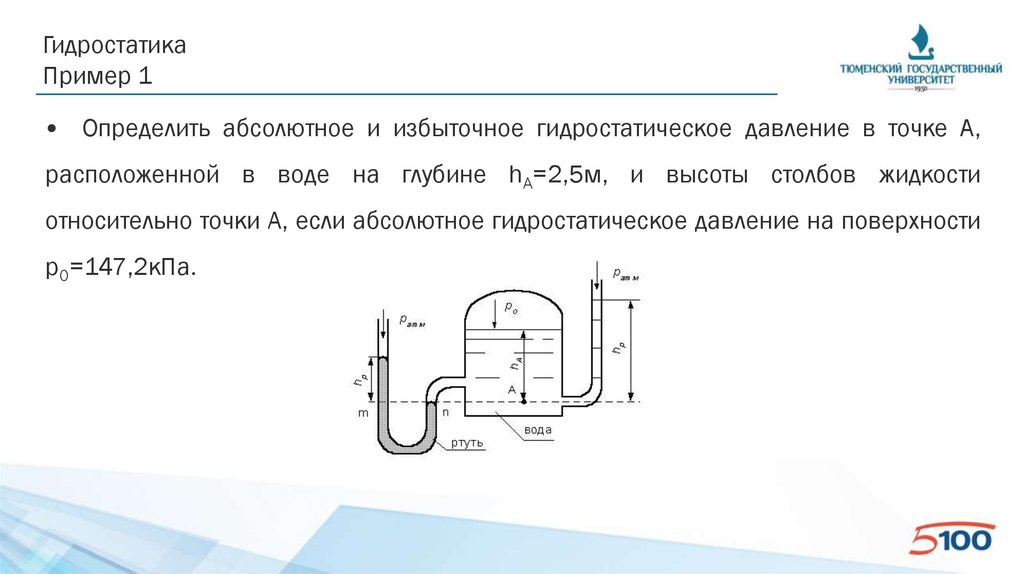
ГидростатикаПример 1
• Определить абсолютное и избыточное гидростатическое давление в точке А,
расположенной в воде на глубине hA=2,5м, и высоты столбов жидкости
относительно точки A, если абсолютное гидростатическое давление на поверхности
p0=147,2кПа.
77.
ГидростатикаПример 1
• Согласно основному уравнению гидростатики:
pабс = p0 + ρ*g*h = 171,7кПа
• Избыточное давление:
pизб = pабс - pатм = 70,375кПа
• Высота столба жидкости равна (ρрт = 13,6*103кг/м3):
hp = pизб/ρ/g
78.
ГидростатикаПример 2
• Определить давление p0 в резервуаре и высоту подъема уровня h1 в трубке 1,
если показания ртутного манометра h2 = 0,15м, h3 = 0,8м
79.
ГидростатикаПример 2
• Условие равновесия для ртутного манометра для плоскости:
pатм = p0 + ρв*g*h3 + ρрт*g*h2
p0 = pатм - ρв*g*h3 - ρрт*g*h2
• Условие равновесия трубки 1:
p0 + ρв*g*h1 = pатм
80.
ГидростатикаЗадача 1
• Определить избыточное давление в трубопроводе А, если высота столба ртути
по пьезометру h2 = 25 см. Центр трубопровода расположен на h1 = 40 см ниже
линии раздела между водой и ртутью.
81.
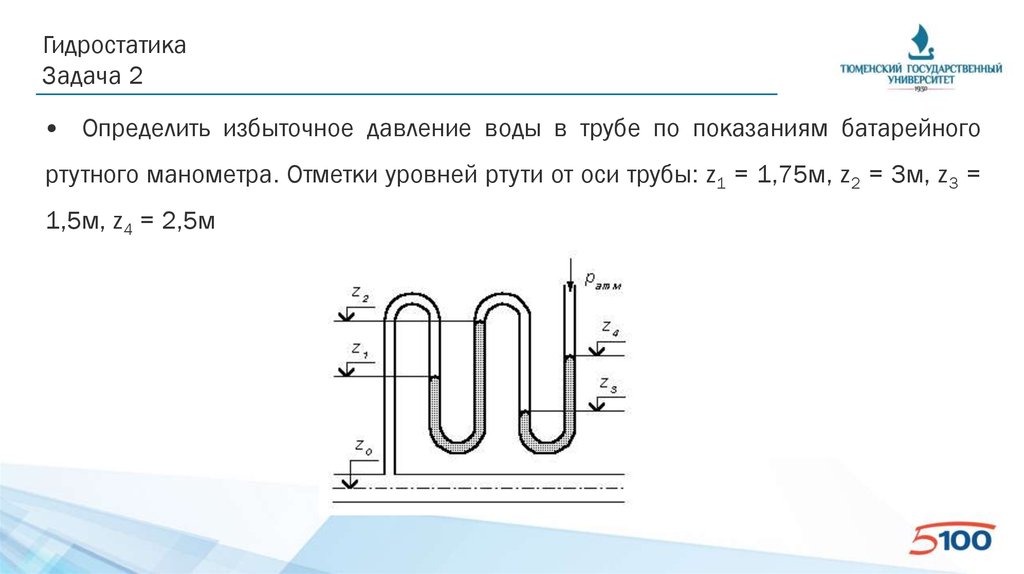
ГидростатикаЗадача 2
• Определить избыточное давление воды в трубе по показаниям батарейного
ртутного манометра. Отметки уровней ртути от оси трубы: z1 = 1,75м, z2 = 3м, z3 =
1,5м, z4 = 2,5м
82.
ГидростатикаЗакон Паскаля
• Давление, производимое на жидкость или газ, передается в любую точку без
изменений во всех направлениях
83.
ГидростатикаДавление на стенки сосуда
• Объединяем закон Паскаля и основное уравнение гидростатики:
p = p0 + ρ*g*h
84.
ГидростатикаЗакон Архимеда
• На тело, погружённое в жидкость (или газ), действует выталкивающая сила,
равная весу жидкости (или газа) в объёме погруженной части тела
FA = ρ*g*V
• Закон Архимеда можно объяснить при помощи разности гидростатических
давлений на примере прямоугольного тела
pB – pA = ρ*g*h
FB – FA = ρ*g*h*S
85.
ГидростатикаУсловия плавания тел
• FA < FT — тело тонет
• FA = FT — тело плавает в жидкости или газе
• FA > FT — тело всплывает до тех пор, пока не начнёт плавать
• ρA < ρT — тело тонет
• ρA = ρT — тело плавает в жидкости или газе
• ρA > ρT — тело всплывает до тех пор, пока не начнёт плавать
86.
ГидростатикаРавновесие плавающего тела
• Для однородного тела плавающего на поверхности справедливо соотношение
Vпогр/V = ρт/ρж
87.
ГидростатикаПримеры расчётов
• Определить, будет ли плавать на поверхности воды прямоугольная баржа,
имеющая длину l = 50 м, ширину b = 3 м и высоту бортов h = 1 м.
Масса
баржи
с
размещенным
на
ней
грузом
равна
120
тонн.
Плотность воды принять равной ρ = 1000 кг/м3, ускорение свободного падения g =
9,81 м/с2
• Вес тела в воде в 2,7 раза меньше, чем в воздухе. Какая плотность вещества,
из которого изготовлено тело?
88.
ГидростатикаПримеры расчётов
• Полый железный шар взвешивают в воздухе и керосине. Показания
динамометра соответственно равны 2,59 Н и 2,16 Н. Определить объем
внутренней полости. Выталкивающей силой воздуха пренебречь.
• Лёд плавает в сосуде. Лёд растаял. Как изменится уровень воды?
• Пластиковая коробка с железками плавает в сосуде. Железки выпали за борт.
Тот же вопрос.
• Лёд с замороженными железками (с полостью) внутри плавает в сосуде. Лед
растаял. Тот же вопрос.
89.
ГидростатикаПримеры расчётов
• 1600 кг/м3
• 2,1*10-5 м3
90.
Течение жидкости в трубопроводе91.
Течение жидкости в трубопроводе• Режимы течения жидкости в трубопроводе
• Законы сохранения энергия, массы и импульса
• Кинематика жидкости
• Динамика жидкости
• Уравнение Эйлера
• Уравнение Бернулли
• Уравнение Навье-Стокса
• Уравнение Эйлера
92.
Течение жидкости в трубопроводеРежимы течения жидкости в трубопроводе
• Режимы течения жидкости и газов разделяют на два класса:
- ламинарные (струйные) - при невысокой скорости течения слои (потоки частиц)
почти не перемешиваются и движутся по параллельным траекториям
- турбулентные - после преодоления некоего критического значения (для различных
условий оно разное), названного числом Рейнольдса, режимы течения жидкости
меняются: струйный поток становится хаотичным, вихревым. Важное свойство
турбулентности: оно всегда трехмерно.
93.
Течение жидкости в трубопроводеЧисло Рейнольдса
• В трубах, имеющих круглое сечение (такие используют для монтажа напорных
трубопроводов), свое число Рейнольдса – формула критического состояния
описывается так: Re = 2300. Для течения по открытому руслу число Рейнольдса
другое: Re = 900. При меньших значениях Re течение будет упорядоченным, при
больших – хаотичным.
Recr = (ρudэ/µ)cr
ρ – плотность потока, u – характерная скорость потока; L – характерный размер
потока (эквивалентный диаметр), µ – коэффициент динамической вязкости, cr –
течение по трубе с круглым сечением, П – смоченный периметр
94.
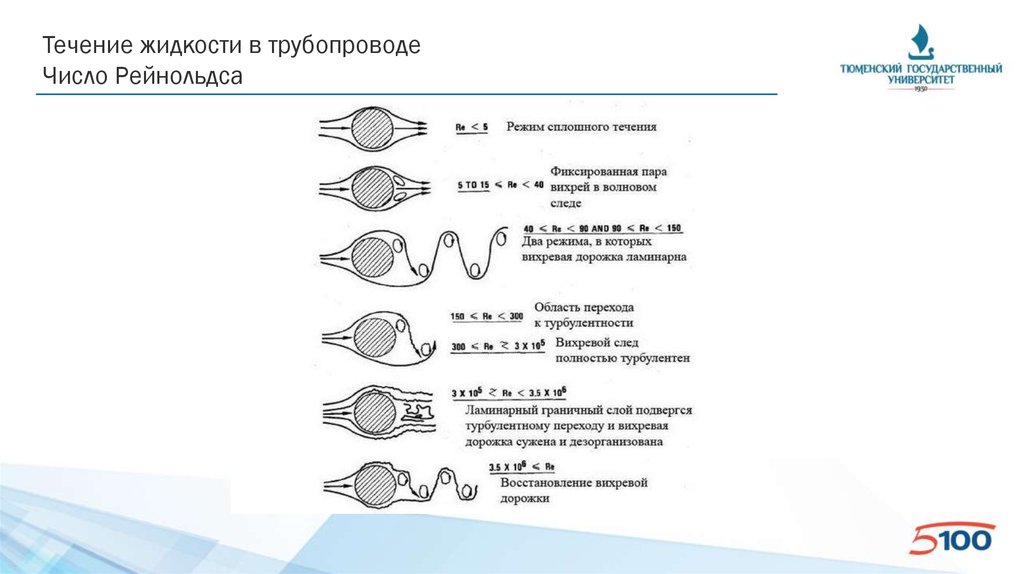
Течение жидкости в трубопроводеЧисло Рейнольдса
95.
Течение жидкости в трубопроводеПримеры
• По трубопроводу диаметром 270×10 мм перекачивается вода с расходом 150
м3/час. Определить скорость воды в трубе и режим её движения.
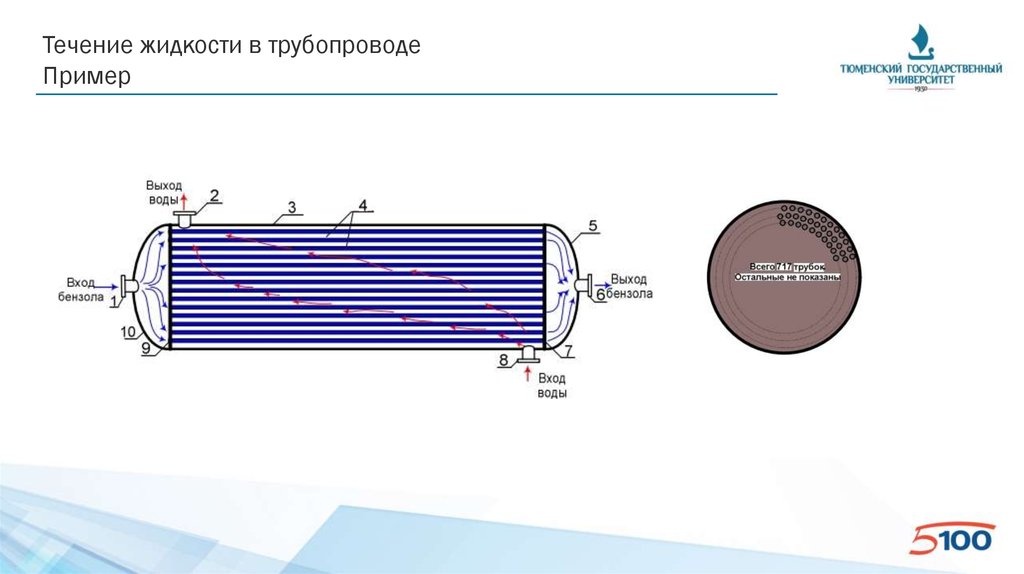
• Бензол с расходом 200 т/час и средней температуре 40ºС поступает в трубный
пучок одноходового кожухотрубчатого теплообменника, состоящего из 717 труб
диаметром d×δ = 20×2 мм. Определить скорость бензола в трубах трубного пучка и
режим его движения в них.
96.
Течение жидкости в трубопроводеПример
97.
Течение жидкости в трубопроводеПримеры
• Для охлаждения бензола в межтрубное пространство кожухотрубчатого
теплообменника с диаметром кожуха D=800 мм подаётся вода со средней
температурой 30ºС. Скорость воды в межтрубном пространстве должна быть 0,5
м/с. Необходимо определить расход воды в м3/час и режим её движения.
98.
Течение жидкости в трубопроводеУравнение непрерывности
∇ — дивергенция,
ρ — количество величины q на единицу объёма (плотность величины q),
t — время,
j — плотность потока величины q,
σ — добавление q на единицу объёма в единицу времени. Члены, которые
добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками»
соответственно.
99.
Течение жидкости в трубопроводеУравнение сохранения
• Если q — сохраняющаяся величина
• Уравнение сохранения массы
j = ρv – плотность потока жидкости
100.
Течение жидкости в трубопроводеПримеры
• На трубопроводе имеется переход с диаметра 50 мм на диаметр 100 мм
(диаметры внутренние). По трубопроводу движется вода, имеющая температуру
20ºС. Её скорость в узком сечении 1,5 м/с. Определить:
1. объёмный и массовый расходы воды;
2. скорость воды в широком сечении;
3. режимы течения в узком и широком сечениях.
101.
Течение жидкости в трубопроводеПримеры
• Азот с расходом 6400 м3/час (при н.у.) подаётся в трубный пучок одноходового
кожухотрубчатого теплообменника. Абсолютное давление газа 3 кГс/см2 (1 кГс =
9,80665 Н). Температура на входе в трубный пучок 120°С, на выходе 30°С. Число
труб в аппарате 379 шт., их диаметр 16×1,5 мм. Определить:
1. скорость азота на входе в трубный пучок и на выходе из него;
2. режим движения азота на входе и на выходе.
102.
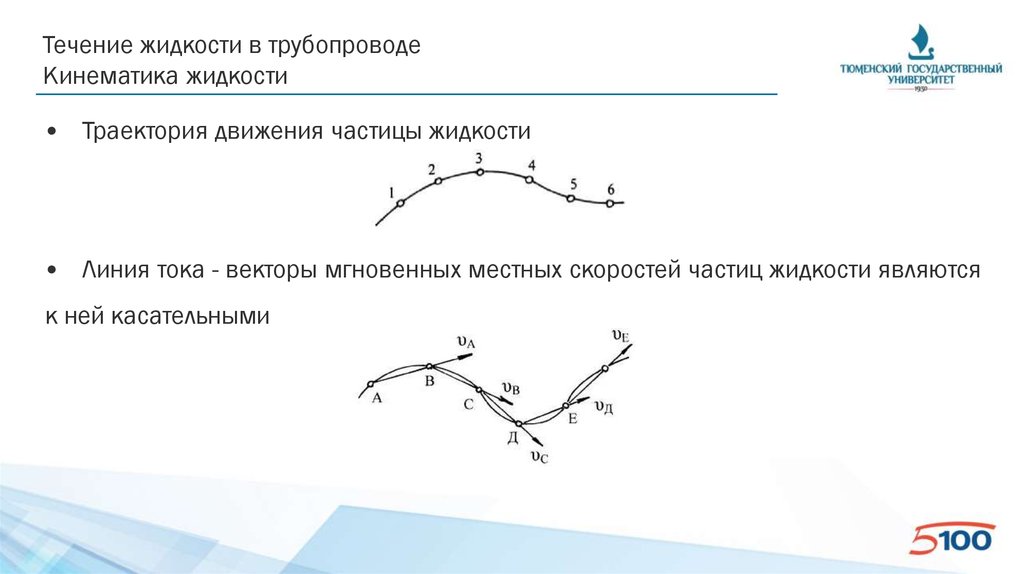
Течение жидкости в трубопроводеКинематика жидкости
• Траектория движения частицы жидкости
• Линия тока - векторы мгновенных местных скоростей частиц жидкости являются
к ней касательными
103.
Течение жидкости в трубопроводеХарактер движения жидкости
• Установившееся (стационарное) движение – это движение, когда в каждой
точке области, где движется жидкость, местные скорости во времени не
изменяются: u = ƒ(х, у, z)
• Неустановившемся движением называют течение жидкости, когда в точках
области, где движется жидкость, местные скорости изменяются с течением
времени и его описывают уравнением u = ƒ(х, у, z, t). При неустановившемся
движении линии тока и траектории частиц не совпадают.
104.
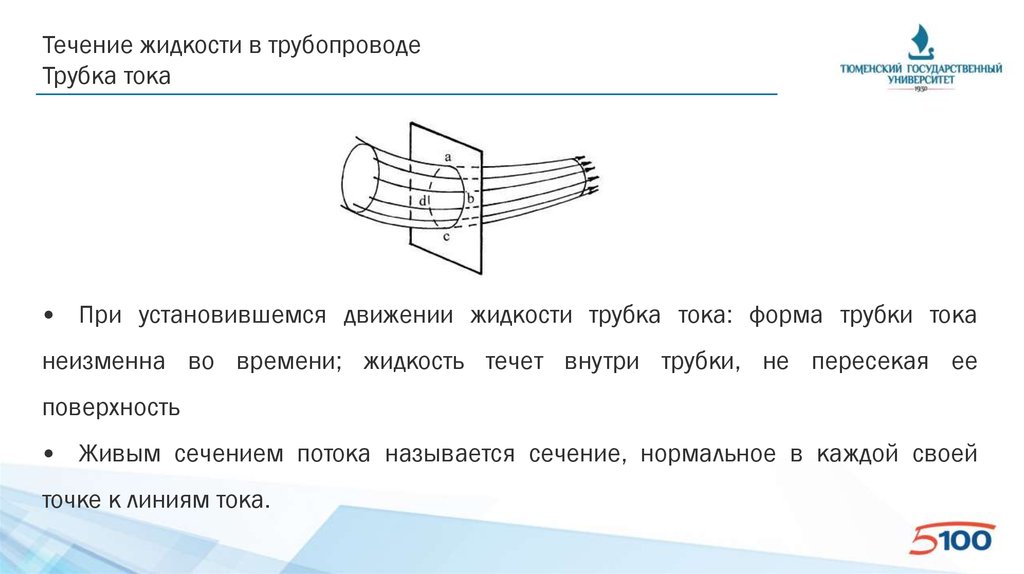
Течение жидкости в трубопроводеТрубка тока
• При установившемся движении жидкости трубка тока: форма трубки тока
неизменна во времени; жидкость течет внутри трубки, не пересекая ее
поверхность
• Живым сечением потока называется сечение, нормальное в каждой своей
точке к линиям тока.
105.
Течение жидкости в трубопроводеРасход. Уравнение расхода
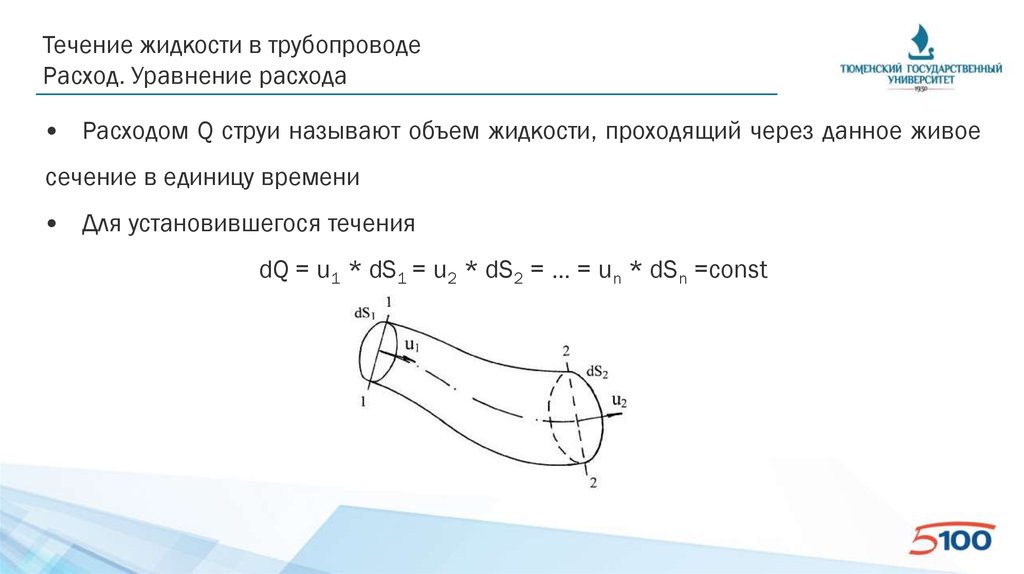
• Расходом Q струи называют объем жидкости, проходящий через данное живое
сечение в единицу времени
• Для установившегося течения
dQ = u1 * dS1 = u2 * dS2 = … = un * dSn =const
106.
Течение жидкости в трубопроводеПотоки жидкости
• Потоком жидкости называют движущуюся массу жидкости, ограниченную
направляющими твердыми поверхностями, поверхностями раздела жидкостей или
свободными поверхностями:
- безнапорные потоки ограничены частично твердой, частично свободной
поверхностью
- напорные потоки ограничены твердыми поверхностями по всему сечению, и
гидродинамическое давление в любой точке потока отлично от атмосферного
- гидравлические струи ограничены только жидкостью или газовой средой.
107.
Течение жидкости в трубопроводеГидравлические элементы потока
• Смоченный периметр χ представляет собой длину линии, по которой жидкость в
живом сечении соприкасается с твердыми поверхностями, ограничивающими
поток
• Гидравлический радиус R - отношение площади живого сечения потока к
смоченному периметру в этом сечении
R = S/χ
108.
Течение жидкости в трубопроводеДинамика жидкости
• Уравнение Бернулли
• Измерение расходов и скоростей жидкости
• Примеры расчётов
109.
Течение жидкости в трубопроводеУравнение Бернулли
• Уравнение Бернулли для элементарной струйки идеальной несжимаемой
жидкости
z1 + p1/ρ/g + (u1)2/2/g = z2 + p2/ρ/g + (u2)2/2/g
• Полный напор в данном сечении струйки = геометрический +
пъезометрический напор + скоростной напор = const
110.
Течение жидкости в трубопроводеЭнергетическая интерпретация уравнения Бернулли
z1 + p1/ρ/g + (u1)2/2/g = const
• Полная удельная энергия = удельная потенциальная энергия + удельная энергия
давления (сжатия) + удельная кинетическая энергия = const
• Удельная потенциальная энергия + удельная энергия давления (сжатия) =
удельная потенциальная энергия
111.
Течение жидкости в трубопроводеУравнение Бернулли для реальной жидкости
• Уравнение Бернулли для элементарной струйки идеальной несжимаемой
жидкости
z1 + p1/ρ/g + α1(u1)2/2/g = z2 + p2/ρ/g + α2(u2)2/2/g + hтр
• α1 и α1 – коэффициенты Кариолиса в двух сечениях, hтр – потери удельной
энергии (напора) на участке между сечениями
112.
Течение жидкости в трубопроводеУравнение Бернулли для реальной жидкости
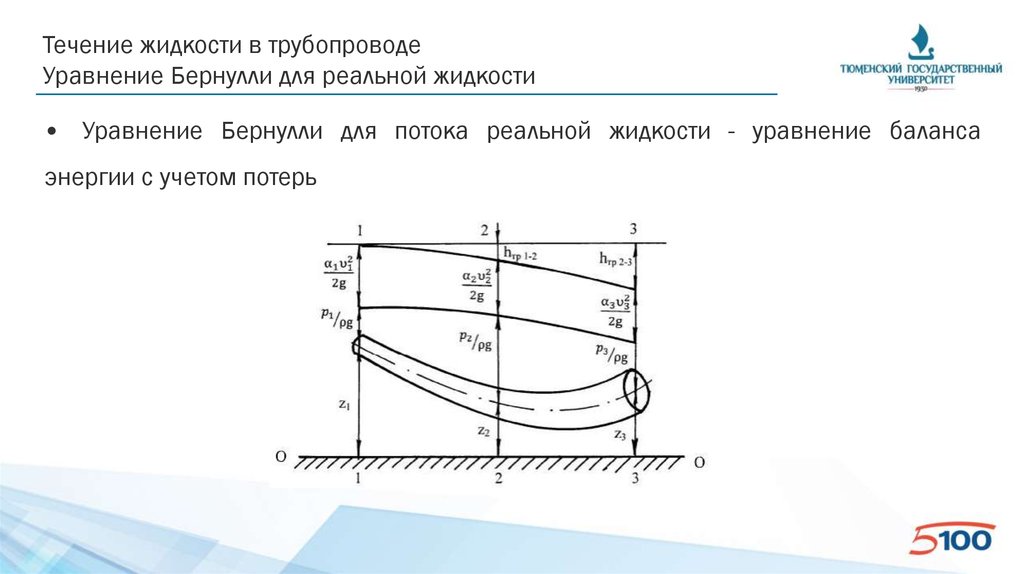
• Уравнение Бернулли для потока реальной жидкости - уравнение баланса
энергии с учетом потерь
113.
Течение жидкости в трубопроводеУравнение Бернулли. Напорная линия
• Гидравлический уклон J - отношение потерь напора hтр к длине участка ℓ, на
котором эти потери происходят
J = hтр/ℓ
• Коэффициент α - коэффициент кинетической энергии или коэффициент
Кариолиса. Коэффициент учитывает неравномерность распределения скоростей
частиц жидкости в сечении реального потока (в пределах от 1 до 2)
Eк = α1(u1)2/2/g
114.
Течение жидкости в трубопроводеИзмерение расходов и скоростей жидкости
• Объемный способ измерения - жидкость поступает в специальный мерный сосуд,
время наполнения которого фиксируется по секундомеру. Если объем сосуда – V, а
время его наполнения – t, то объемный расход будет равен
Q = V*t
• Весовой способ измерения - находят вес всей жидкости, поступившей в сосуд за
время t, и зная плотность жидкости, определяют весовой расход как
Q = G/(ρgt)
115.
Течение жидкости в трубопроводеИзмерение расходов и скоростей жидкости
• Водомер Вентури
• Трубка Пито
116.
Течение жидкости в трубопроводеУравнение Бернулли. Пример
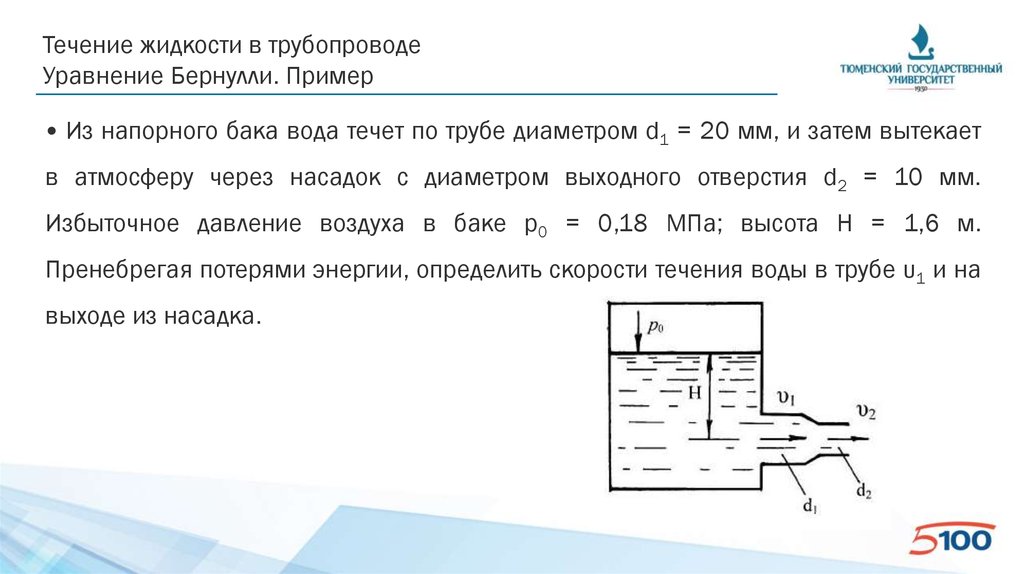
• Из напорного бака вода течет по трубе диаметром d1 = 20 мм, и затем вытекает
в атмосферу через насадок с диаметром выходного отверстия d2 = 10 мм.
Избыточное давление воздуха в баке р0 = 0,18 МПа; высота Н = 1,6 м.
Пренебрегая потерями энергии, определить скорости течения воды в трубе υ1 и на
выходе из насадка.
117.
Течение жидкости в трубопроводеУравнение Бернулли. Пример. Решение
Ввиду значительных размеров сосуда по сравнению с поперечными размерами
трубопровода скорость υ0 будет весьма мала
118.
Течение жидкости в трубопроводеУравнение Бернулли. Пример
• Определить, на какую высоту поднимется вода в трубке, один конец которой
присоединен к суженному сечению трубопровода, а другой конец опущен в воду.
Расход воды в трубе Q=0,025 м3⁄с; избыточное давление р1=49 кПа; диаметры
d1=100 мм и d2=50 мм. Потерями напора пренебречь.
119.
Течение жидкости в трубопроводеУравнение Бернулли. Пример. Решение
120.
Течение жидкости в трубопроводеМетоды Эйлера и Лагранжа
• Метод Эйлера основывается на анализе течения жидкости в различных точках
пространства в данный временной отрезок. Получено из статики.
• Метод Лагранжа основывается на анализе течения каждой частицы жидкости, то
есть траектории их течения.
121.
Течение жидкости в трубопроводеУравнения Эйлера для движущейся идеальной жидкости
• X, Y, Z – проекции единичных массовых сил на соответствующие координатные
оси
122.
Течение жидкости в трубопроводеУравнения Эйлера для движущейся идеальной жидкости
• Уравнения не учитывают ни сил трения, ни вязкости, т.к. уравнения получены из
уравнений статики, а в статических уравнениях данные величины не фигурируют.
• Полем скорости называется совокупность всех мгновенных скоростей.
Изменение этого поля описывается системой уравнений Эйлера.
123.
Течение жидкости в трубопроводеМетод Лагранжа
• Рассматривается движение каждой частицы жидкости
• В начальный момент времени каждая частица имеет координаты x0, y0, z0.
При движении частицы ее координаты зависят от времени
x = x(x0, y0, z0, t); y = y(x0, y0, z0, t); z = z(x0, y0, z0, t)
Здесь x0, y0, z0, t – параметры Лагранжа.
124.
Течение жидкости в трубопроводеУравнения Навье-Стокса
• В векторном виде для несжимаемой жидкости
• При учёте сжимаемости
ν — коэффициент кинематической вязкости, f — векторное поле массовых сил, η —
коэффициент динамической вязкости (сдвиговая вязкость), ζ — «вторая вязкость»,
или объёмная вязкость.
125.
Течение жидкости в трубопроводеУравнения Навье-Стокса
• Система дифференциальных уравнений в частных производных, описывающая
движение вязкой ньютоновской жидкости. Включает уравнение неразрывности
126.
Течение жидкости в трубопроводеУравнения Навье-Стокса. Основные свойства
• При
превышении
числа
Рейнольдса
некоторой
критической
величины
аналитическое точное решение для пространственного или плоского потока даёт
хаотический вид течения (турбулентность). При уменьшении числа Рейнольдса
ниже критического решение опять дает нехаотический вид течения.
• Исключительная чувствительность к изменению коэффициентов уравнения при
турбулентном режиме: при изменении числа Re на 0,05 % решения совершенно
отличаются друг от друга.
127.
Неньютоновские ивысоковязкие жидкости
128.
Неньютоновские жидкости• Неньютоновская жидкость - жидкость, при течении которой её вязкость зависит
от градиента скорости. Такие жидкости сильно неоднородны и состоят из
крупных молекул, образующих сложные пространственные структуры.
• Для неньютоновских жидкостей невозможно использовать уравнения НавьеСтокса
• 1 – ньютоновская, 2 – псевдопластичная, 3 – дилатантная,
4 – вязкопластичная (τ - касательное напряжение)
129.
Высоковязкие жидкости• Особый вид транспортировки, специальные устройства для смешивания.
130.
Высоковязкие жидкости• Особый вид транспортировки, специальные устройства для смешивания.
131.
Структура многофазного потока132.
Структура многофазного потока• Многофазные потоки возникают при протекании газа через жидкость
(пробулькивание, барботаж), жидкости через газ и при транспортировке смеси
жидкости и газа
• Режимы многофазного потока: пузырьковая, пробковый (совокупность больших
и малых, плоских пузырей различной формы, разделенных жидкостными
перемычками), снарядно-пробковая, пробково-кольцевая, кольцевая, дисперсно-
кольцевая, дисперсная
133.
Структура многофазного потокаРежимы многофазного потока
• Пузырьковое движение характеризуется наличием в потоке воды отдельных
пузырьков газа небольших
размеров (порядка 1 мм). Размер
пузырьков, форма и распределение
зависят от величины расхода,
локальной энтальпии, плотности
теплового потока и давления.
134.
Структура многофазного потокаРежимы многофазного потока
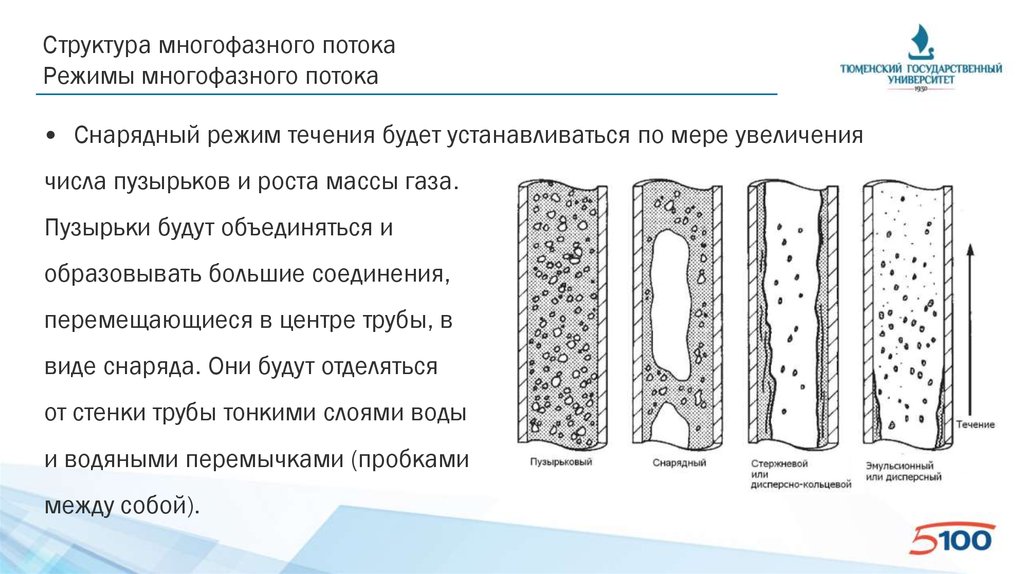
• Снарядный режим течения будет устанавливаться по мере увеличения
числа пузырьков и роста массы газа.
Пузырьки будут объединяться и
образовывать большие соединения,
перемещающиеся в центре трубы, в
виде снаряда. Они будут отделяться
от стенки трубы тонкими слоями воды
и водяными перемычками (пробками
между собой).
135.
Структура многофазного потокаРежимы многофазного потока
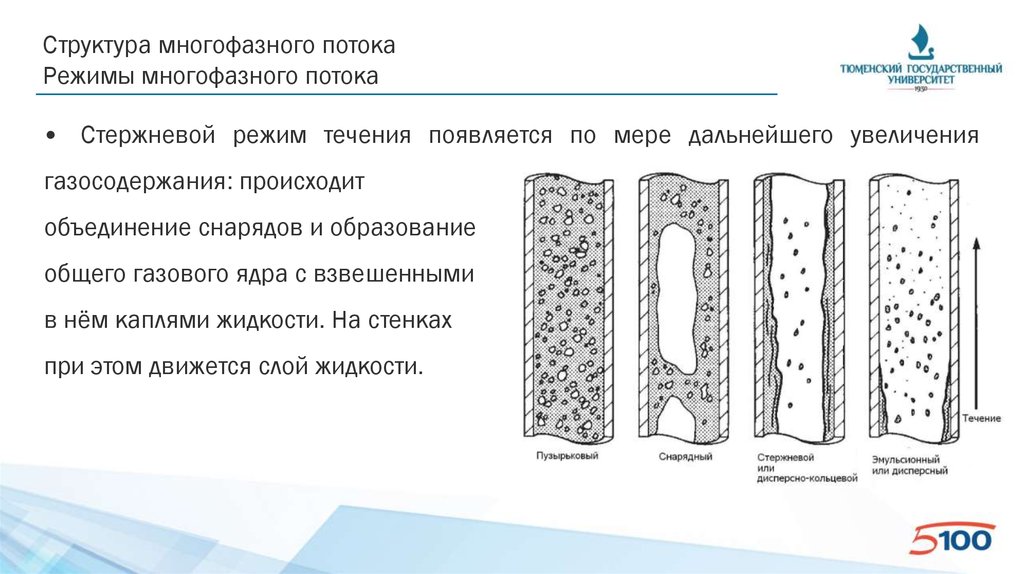
• Стержневой режим течения появляется по мере дальнейшего увеличения
газосодержания: происходит
объединение снарядов и образование
общего газового ядра с взвешенными
в нём каплями жидкости. На стенках
при этом движется слой жидкости.
136.
Структура многофазного потокаРежимы многофазного потока
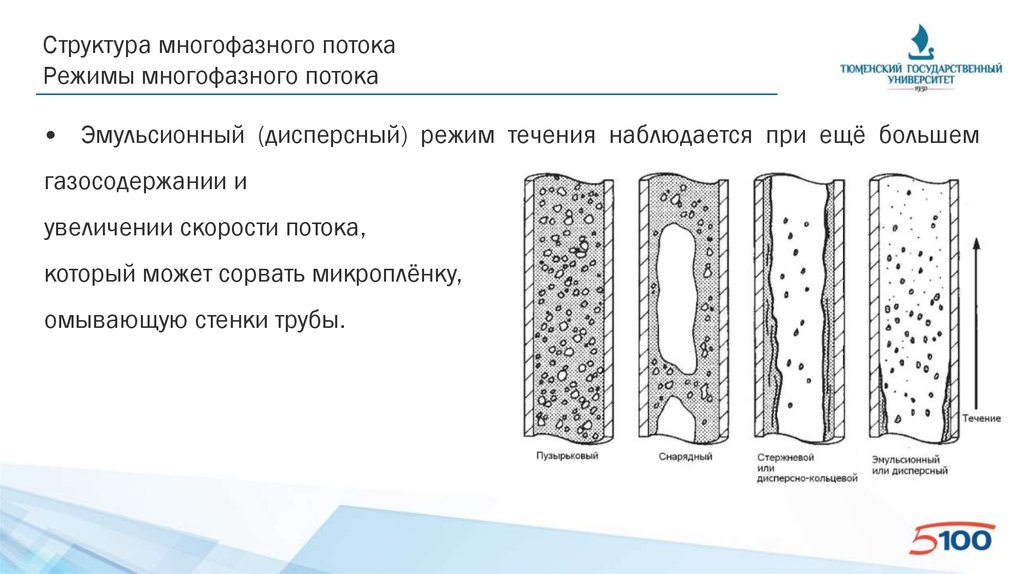
• Эмульсионный (дисперсный) режим течения наблюдается при ещё большем
газосодержании и
увеличении скорости потока,
который может сорвать микроплёнку,
омывающую стенки трубы.
137.
Структура многофазного потокаКарта Тайтеля-Даклера
• Карта Тайтеля-Даклера
1 - Пузырьковый режим;
2 - Пузырьково-снарядный;
3 - Снарядный;
4 - Пенный;
5 - Кольцевой;
6 - Дисперсно-кольцевой.



















































































































 physics
physics








