Similar presentations:
Элементы гемодинамики
1.
Лекция 1.Элементы гемодинамики.
Артериальное давление.
Работа сердца.
Модель Франка.
2.
ВведениеГидродинамика и гидростатика
Идеальная жидкость:
1. Изотропность всех физических свойств
2. Абсолютная несжимаемость
3. Абсолютная текучесть
(отсутствие сил внутреннего трения)
3.
Давление силы на поверхностьF
Fn F cos
p
S
S
S
H
p 2 Па
м
4.
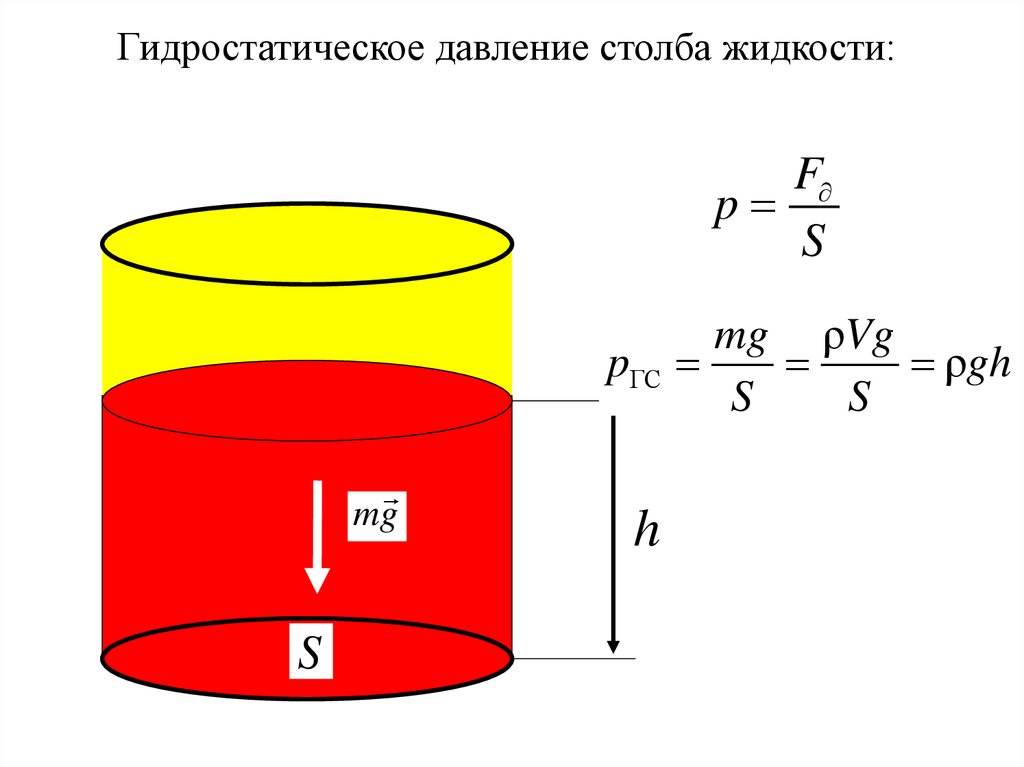
Гидростатическое давление столба жидкости:F
p
S
p С
mg
S
h
mg ρVg
ρgh
S
S
5.
Закон ПаскаляДавление, производимое на поверхность жидкости
(газа), передается во все точки жидкости (газа)
без изменения
Давление во всех горизонтальных сечениях
сообщающихся сосудов одинаково
6.
Основное уравнение гидростатики:p0
h
pабс. p0 gh
7.
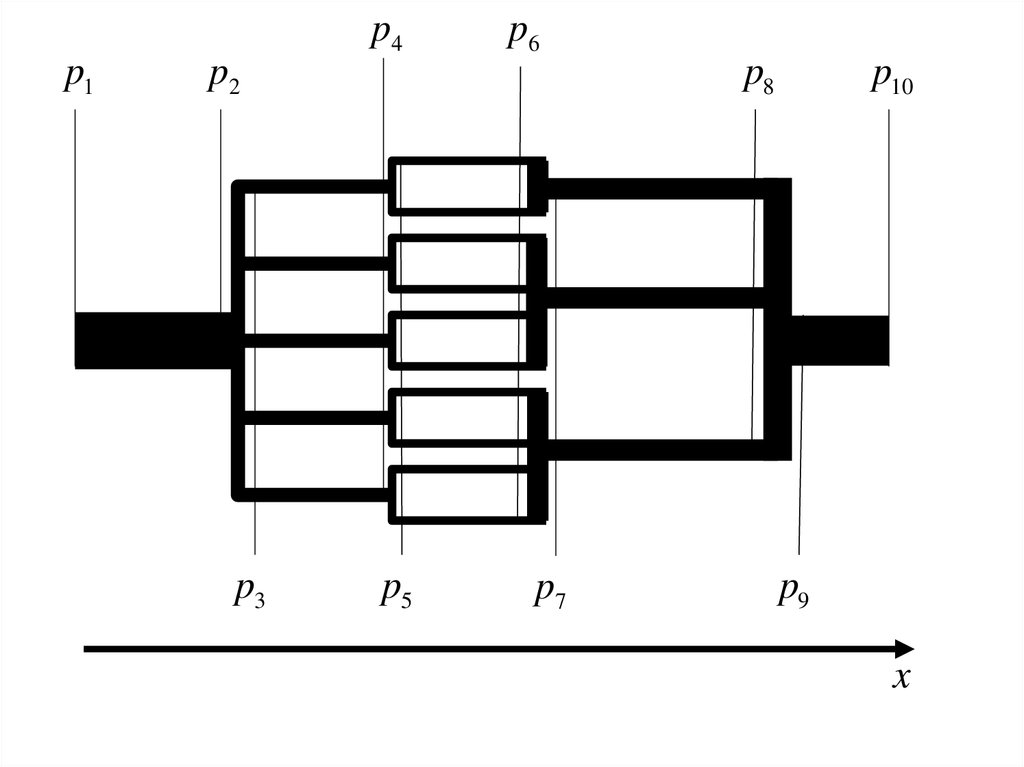
hp1
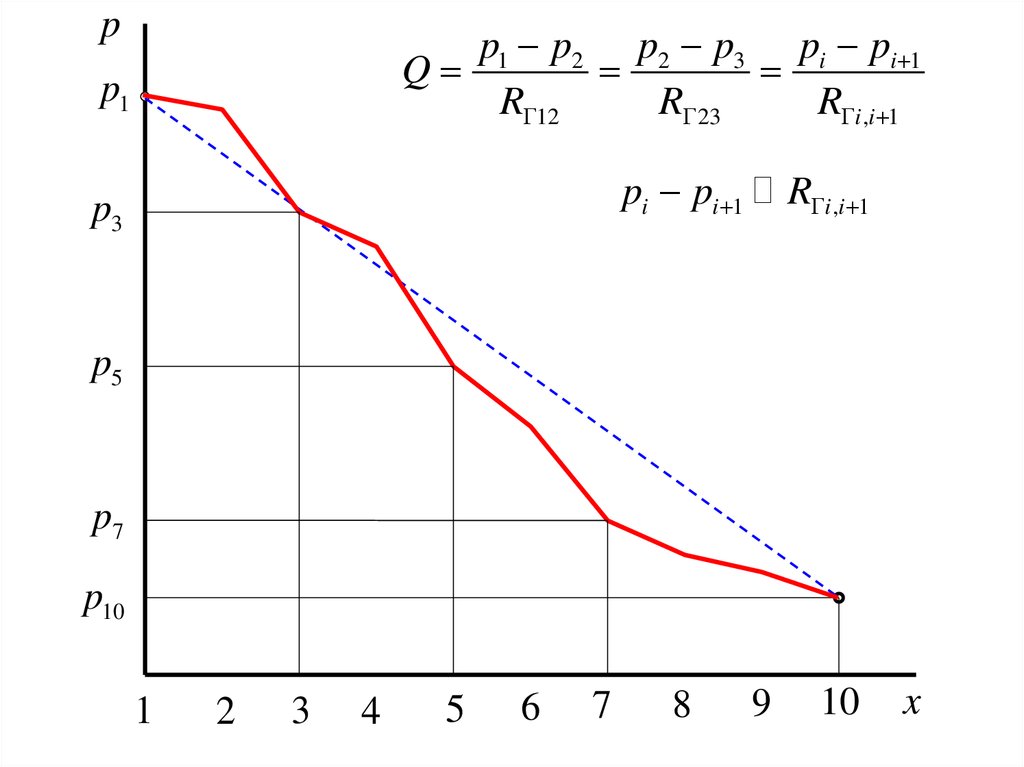
h1
v1
h2
v2
p2
8.
Уравнение неразрывности струи.QV Sv const
Qm ρSv const
Уравнение Бернулли:
v 22
v12
gh2
p2 gh1
p1 const
2
2
9.
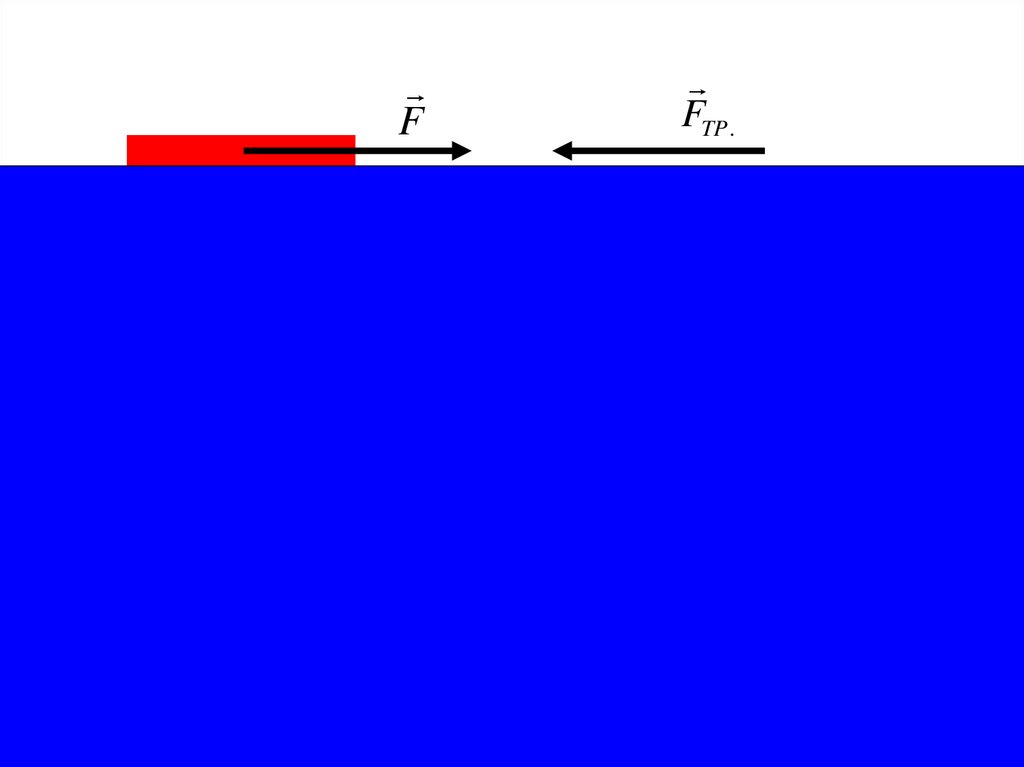
Реальная жидкость - модель природной жидкости,характеризующаяся изотропностью всех физических
свойств, но в отличие от идеальной модели, обладает
внутренним трением при движении
10.
FFTP .
11.
12.
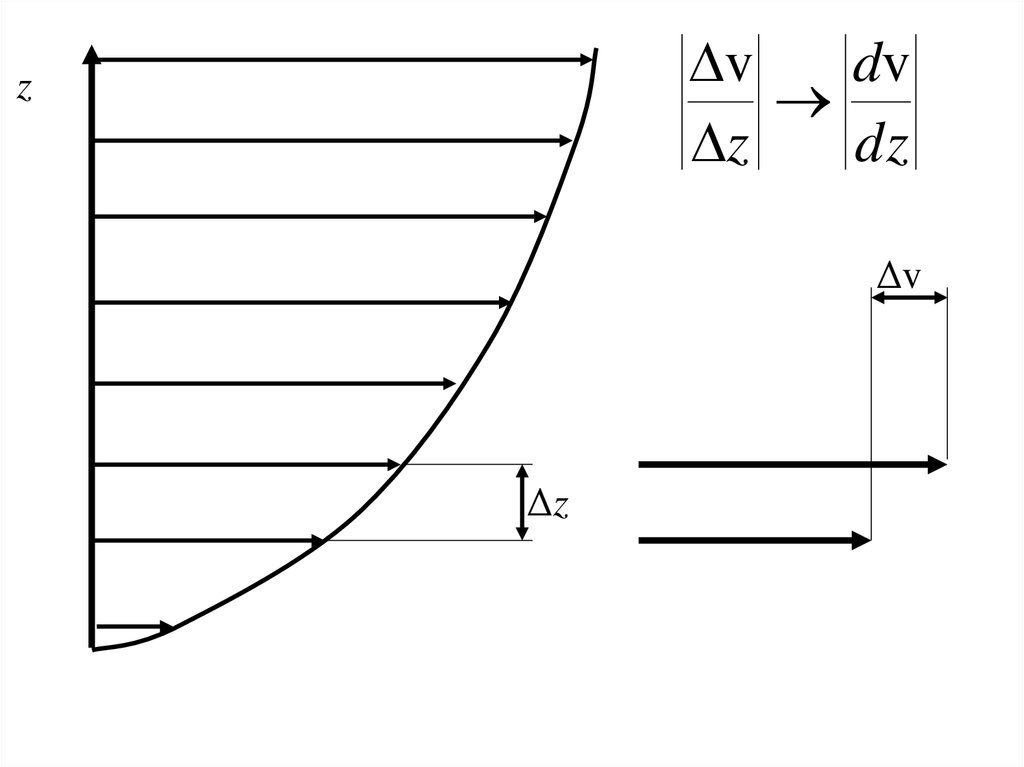
vdv
z
dz
z
Δv
Δz
13.
Закон Ньютона для вязкого трения:FTP .
dv
S
dz
v
F S
z
м
кг
м
F z Н м
кг
с
Па с
м
S v м м
м с
с
с
2
3
2
Коэффициент динамической вязкости
14.
Коэффициент кинематической вязкости:η
ν
ρ
кг
η м с м 2
ν = кг
с
ρ
м3
15.
Ньютоновские жидкостиdv
η f
dz
16.
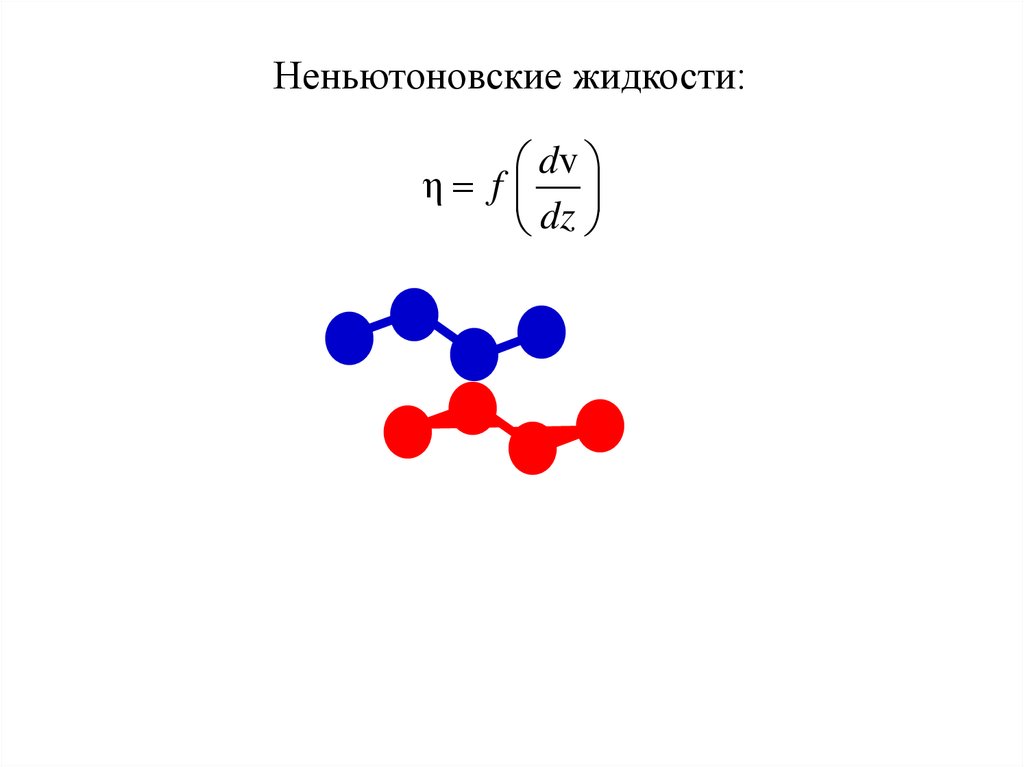
Неньютоновские жидкости:dv
η f
dz
17.
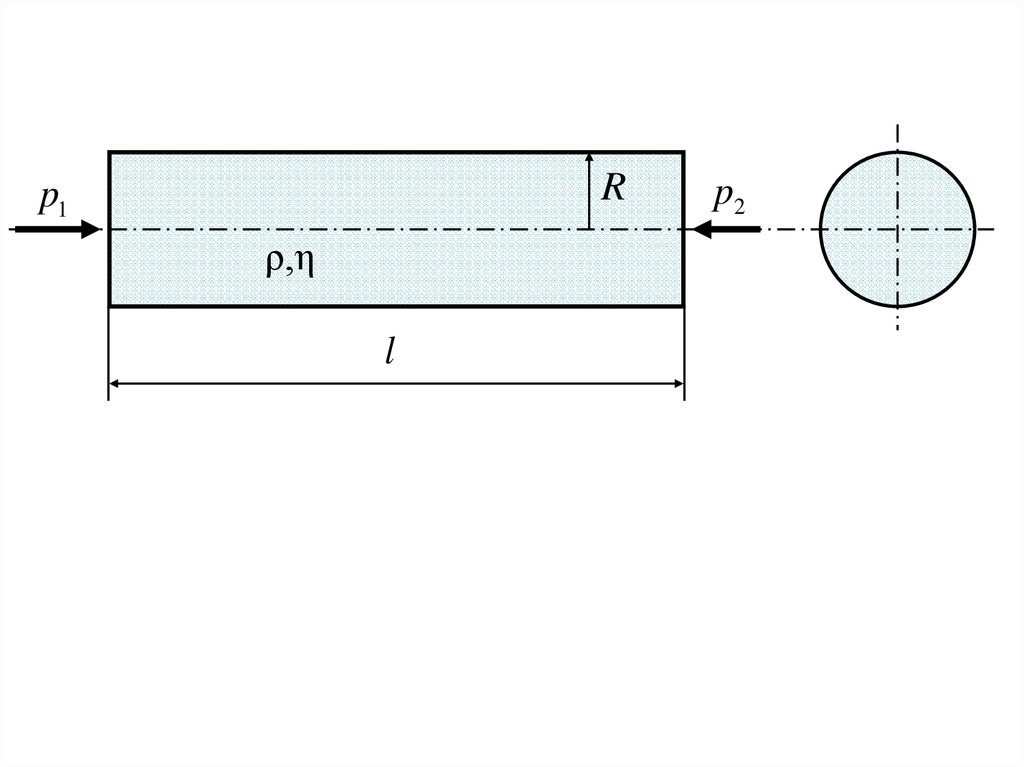
Течение ньютоновской вязкой жидкостипо круглой гладкой трубе с жесткими стенками
Заданы:
длина трубы l;
радиус трубы R;
свойства жидкости: плотность ρ и вязкость η;
перепад давлений на торцах трубы: р1 – р2
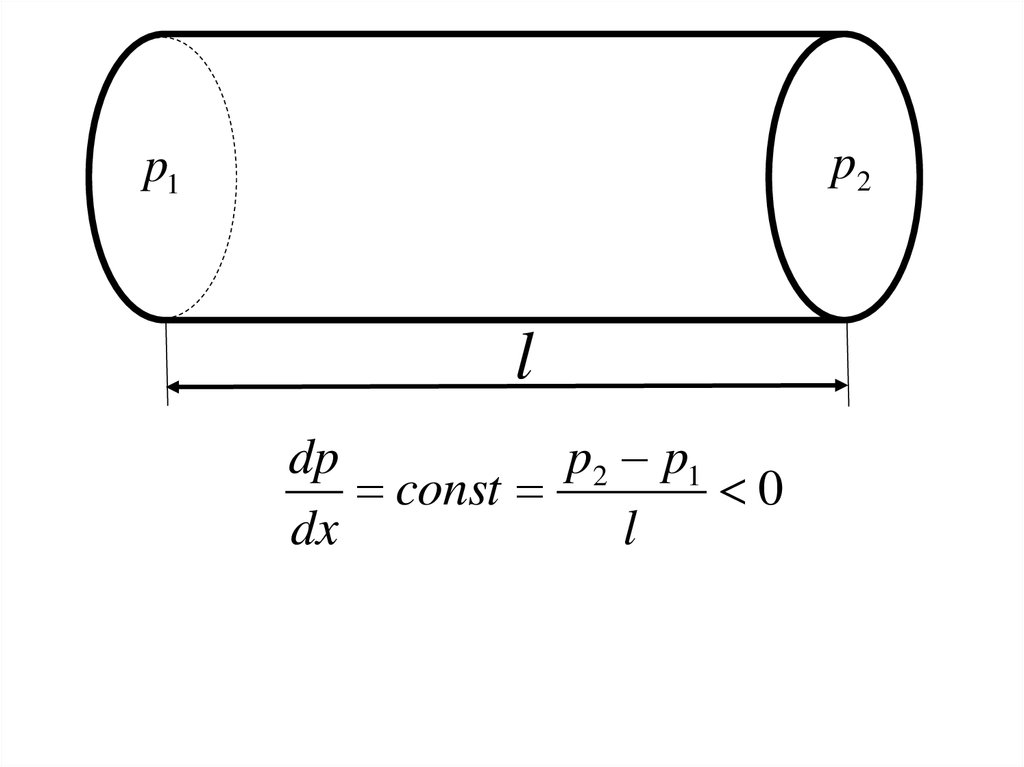
18.
Rp1
ρ,η
l
p2
19.
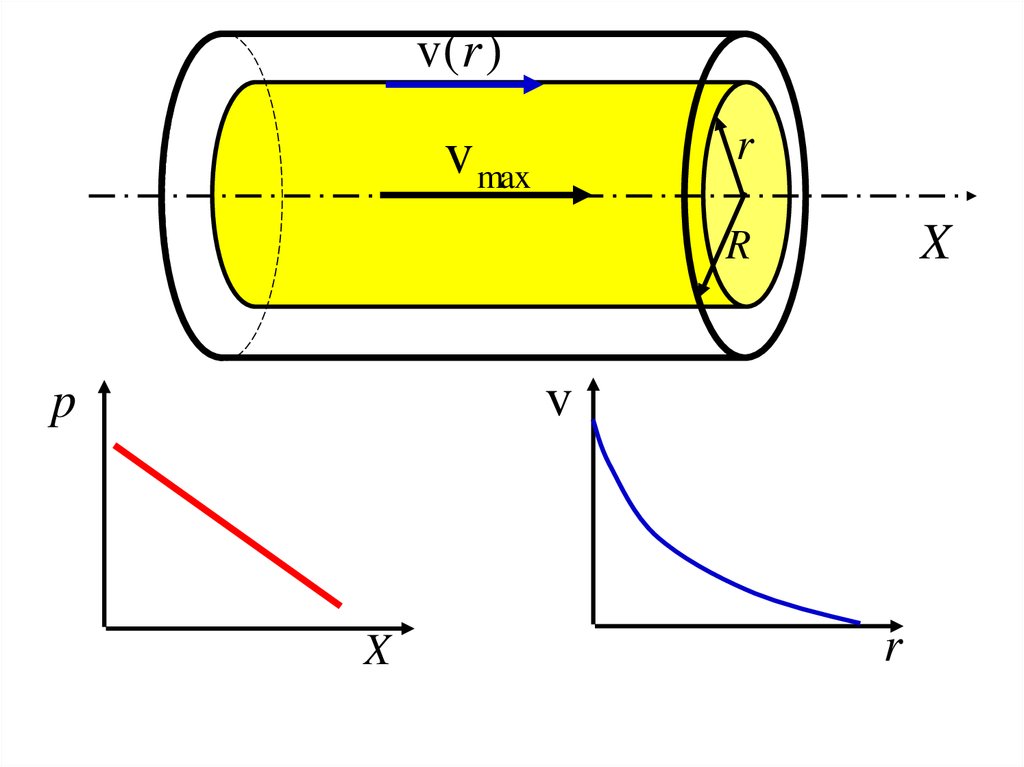
Задачи:1. Описать распределение скоростей частиц жидкости
по сечению трубы
2. Определить расход жидкости через трубу
20.
v(r )r
v max
X
R
v
p
X
r
21.
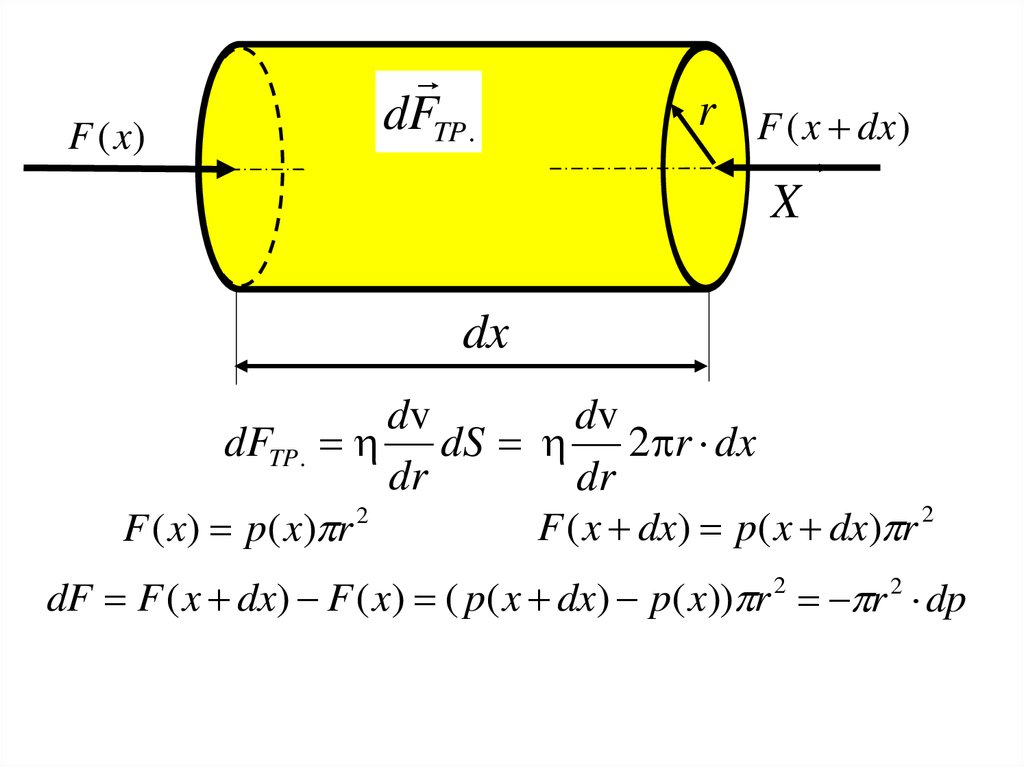
F (x)dFTP .
r F ( x dx)
X
dx
dv
dv
dFTP . dS 2 r dx
dr
dr
2
2
F
(
x
dx
)
p
(
x
dx
)
r
F ( x) p( x) r
dF F ( x dx) F ( x) ( p( x dx) p( x)) r 2 r 2 dp
22.
dpdF r dp r dx
dx
2
2
dFTP. dF 0
dv
2 dp
2 r dx r dx 0
dr
dx
dv
dp
2
r
dr
dx
v( r ) f ( x )
dv
f ( x)
dr
dp
const
dx
23.
p2p1
l
dp
p2 p1
const
0
dx
l
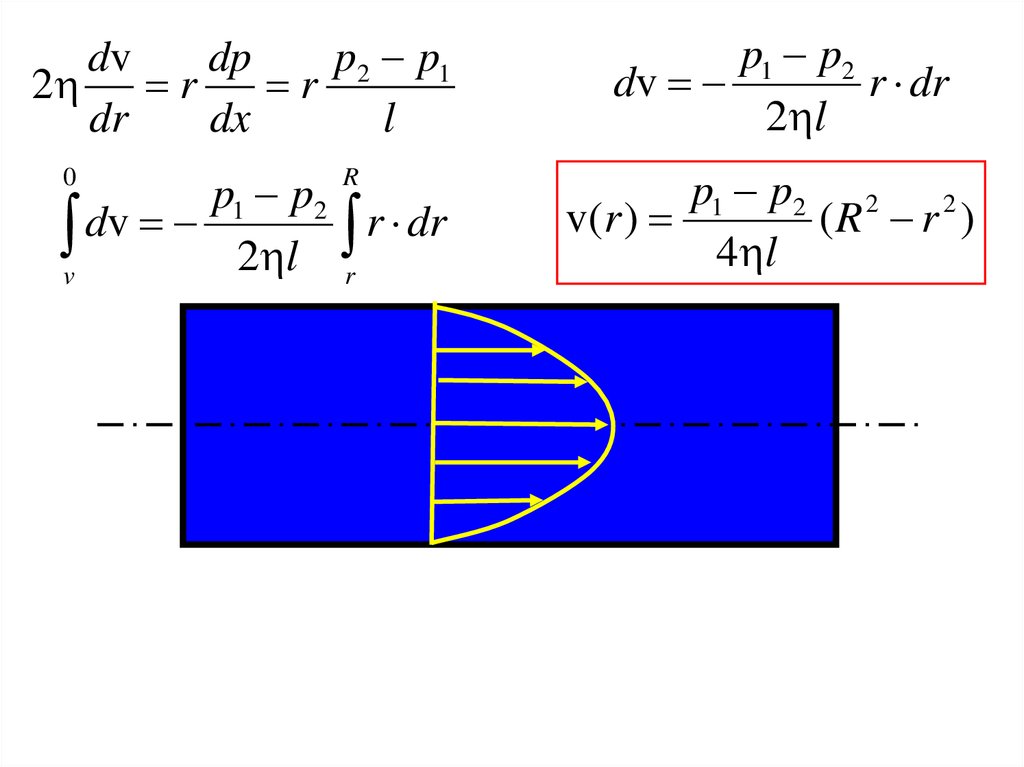
24.
dvdp
p2 p1
2
r
r
dr
dx
l
p1 p2
dv
r dr
2 l
p1 p2
v dv 2 l r r dr
p1 p2 2 2
v( r )
(R r )
4 l
0
R
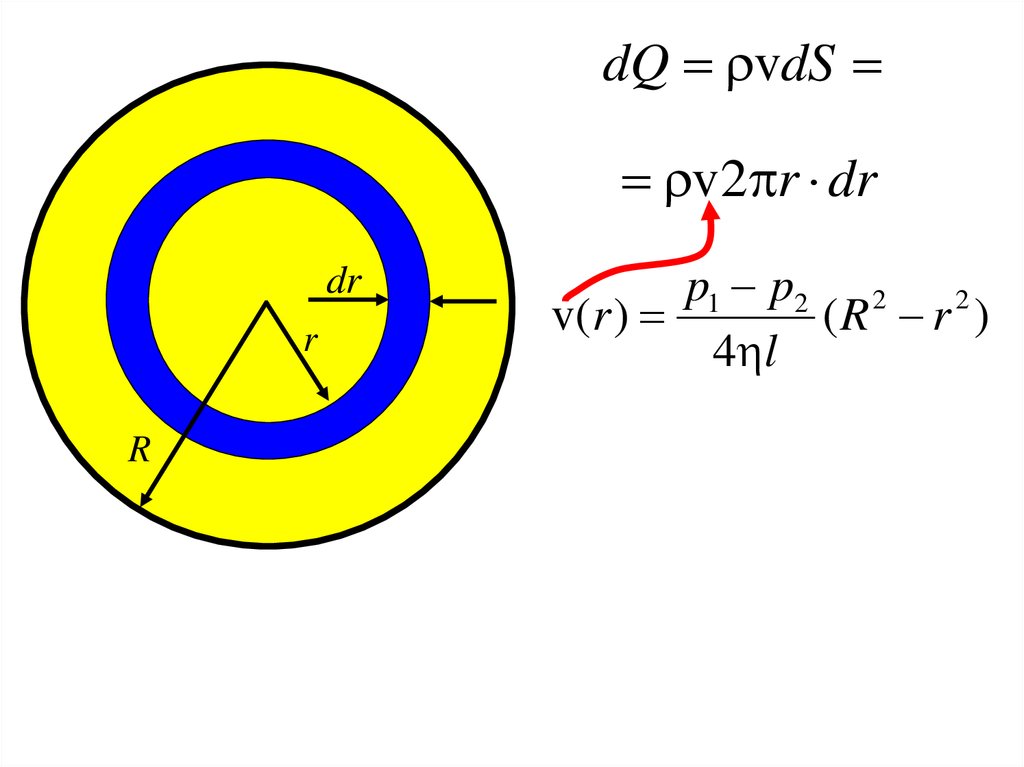
25.
dQ vdSv2 r dr
dr
r
R
p1 p2 2 2
v( r )
(R r )
4 l
26.
p1 p2 2 2dQ
( R r )2 r dr
4 l
p1 p2
2
2
Q dQ 2
(
R
r
)r dr
4 l 0
R
Уравнение Пуазейля:
p1 p2 4
Q πρ
R
8ηl
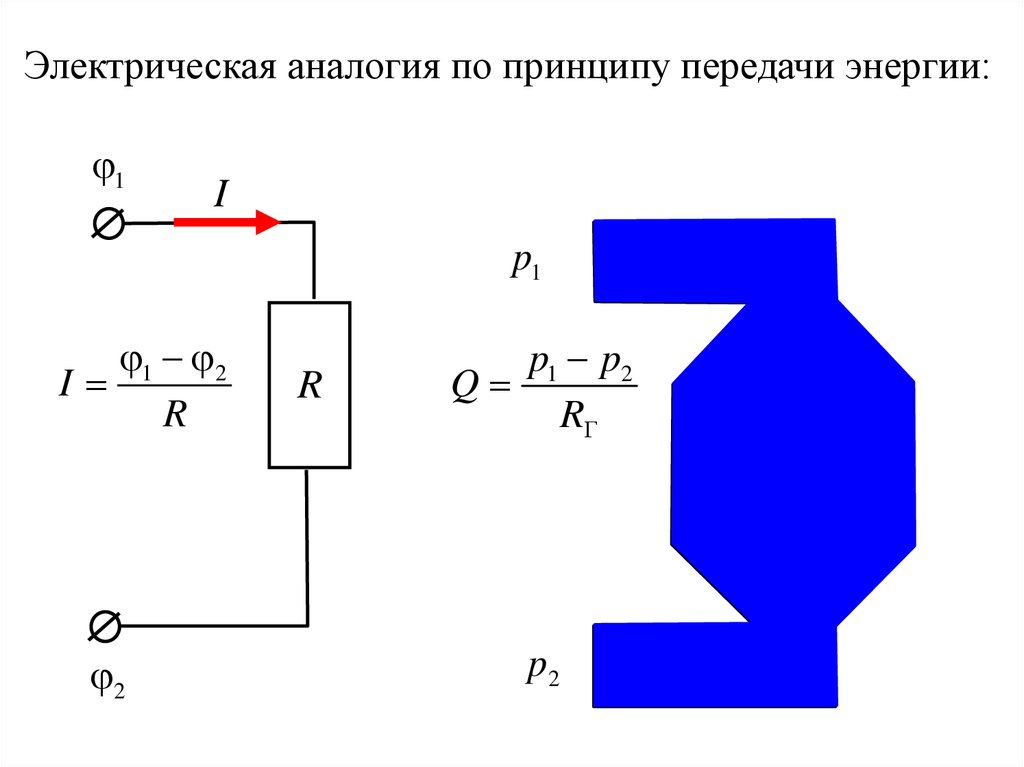
27.
Электрическая аналогия по принципу передачи энергии:1
I
p1
1 2
I
R
2
R
p1 p2
Q
R
p2
28.
Q Ip1 p2 1 2
p1 p2 4
Q π
R
8 l
R
1 2
I
RЭ
8 l
4
R
29.
Ламинарное течение30.
Турбулентное течение31.
Число (критерий)Рейнольдса:
ρvd vd
Re
η
м
м
v d с
Re
м
с
2
32.
Reкритическоекруглые = 2300Re кровикритическое = 970 ± 80
33.
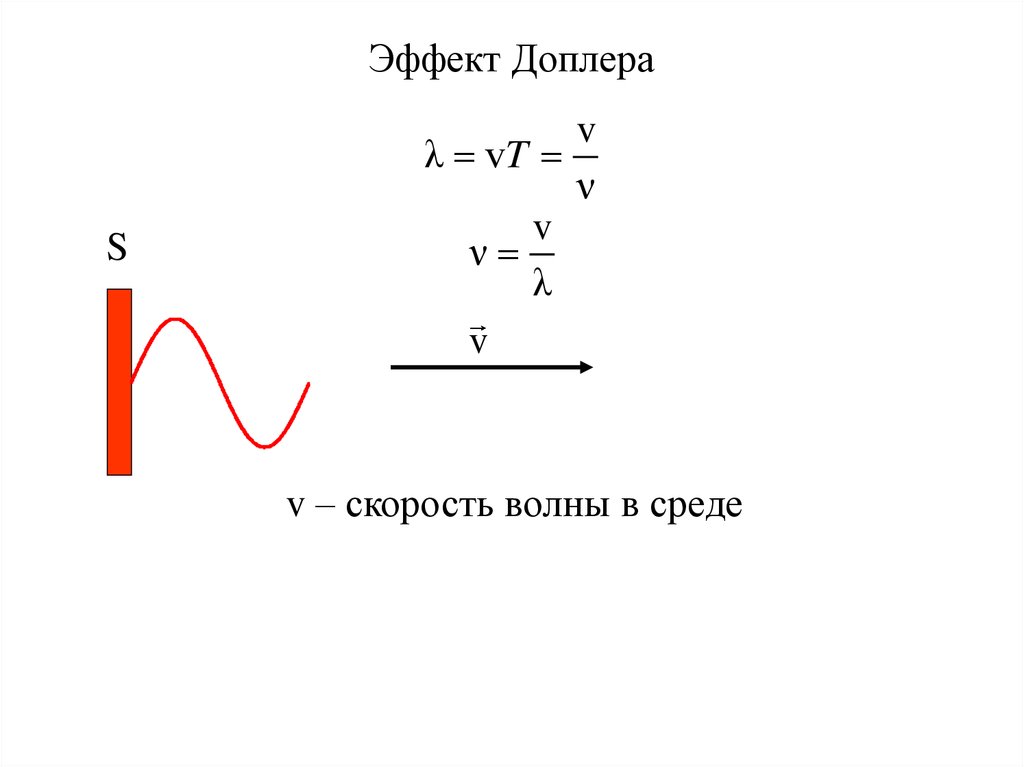
Эффект ДоплераS
v
λ vT
ν
v
ν
λ
v
v – скорость волны в среде
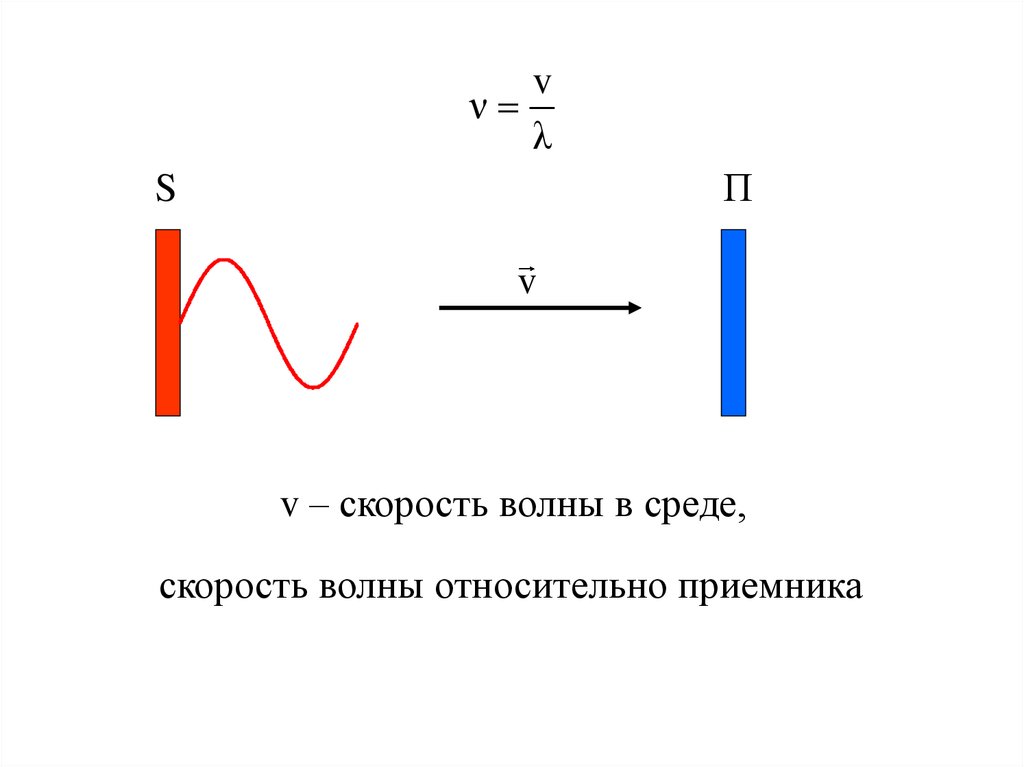
34.
vν
λ
П
S
v
v – скорость волны в среде,
скорость волны относительно приемника
35.
Скорость волны относительно приемникаv
v
v v v
v v v
v v v v v Π v v Π
ν
ν
v
λ
λ
v
ν
36.
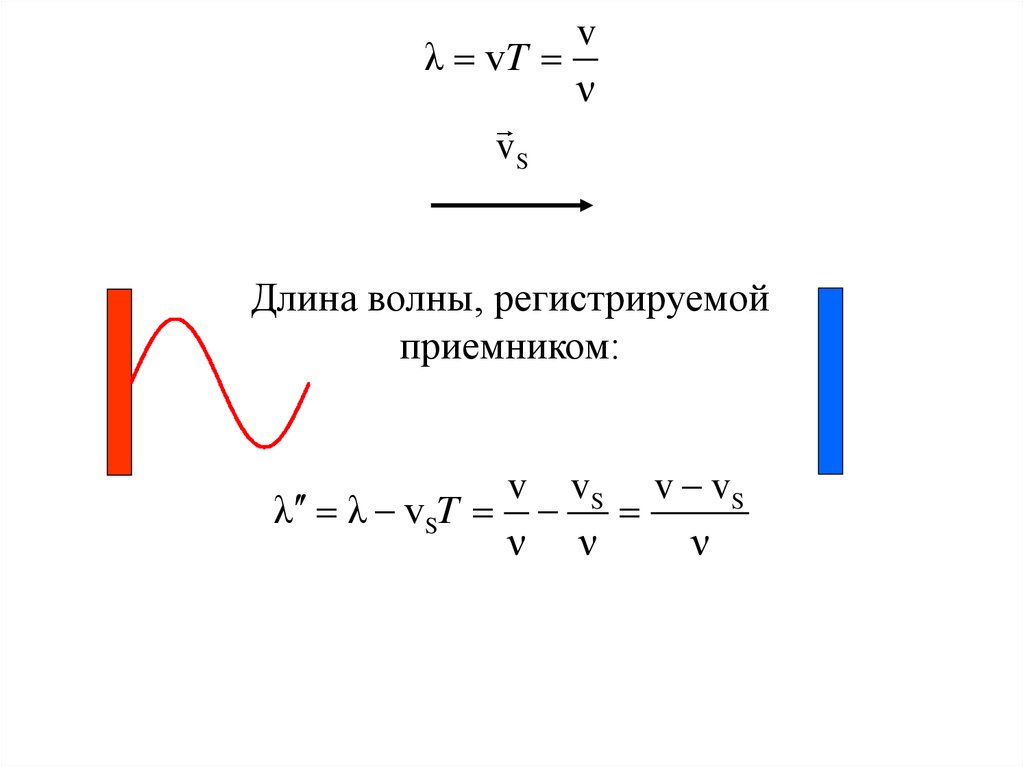
vλ vT
ν
vS
Длина волны, регистрируемой
приемником:
v vS v v S
λ λ vST
ν ν
ν
37.
Частота колебаний, регистрируемая приемником:v – скорость волны в среде,
скорость волны относительно приемника
v
ν
λ
v
v
ν
ν
v vS v vS
ν
38.
Эффект Доплера – изменение частоты волн,регистрируемых приемником, вследствие
относительного движения источника и приемника
v v
ν
ν
v vS
39.
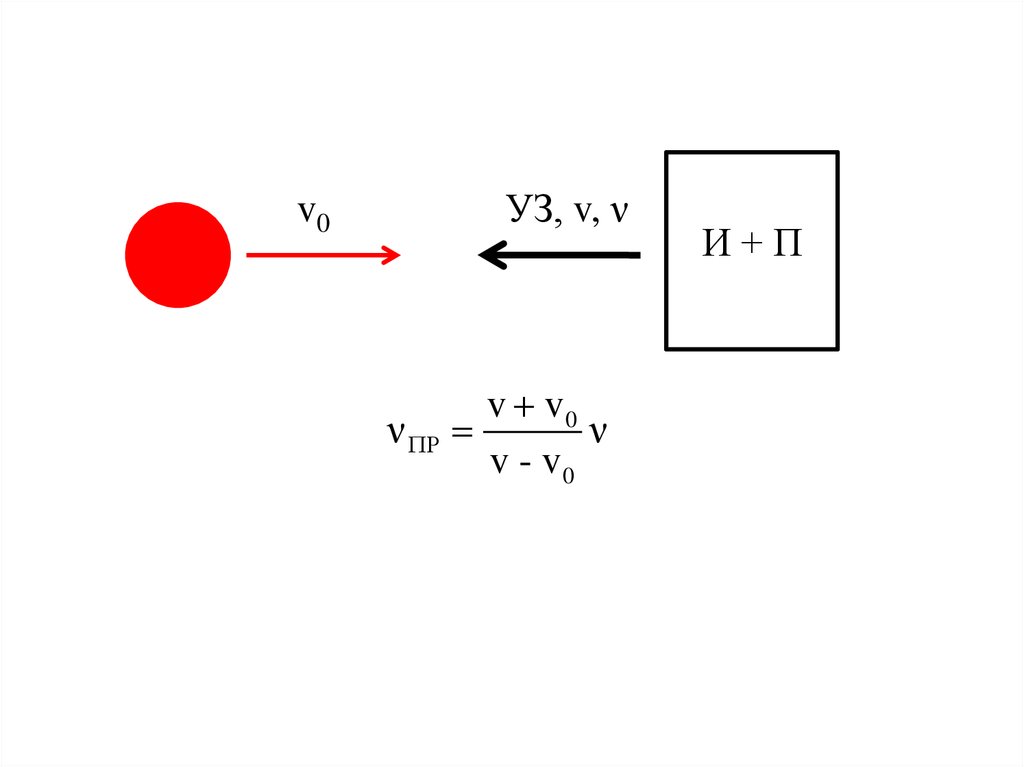
УЗ, v, νv0
ν
v v0
ν
v - v0
И+П
40.
Общие выводы к введению:1. «Движущей силой» течения любой жидкости
является перепад давления
41.
2. Для любых жидкостейсправедливо уравнение неразрывности :
QV Sv const
Qm ρSv const
Для разветвленных трубопроводов:
42.
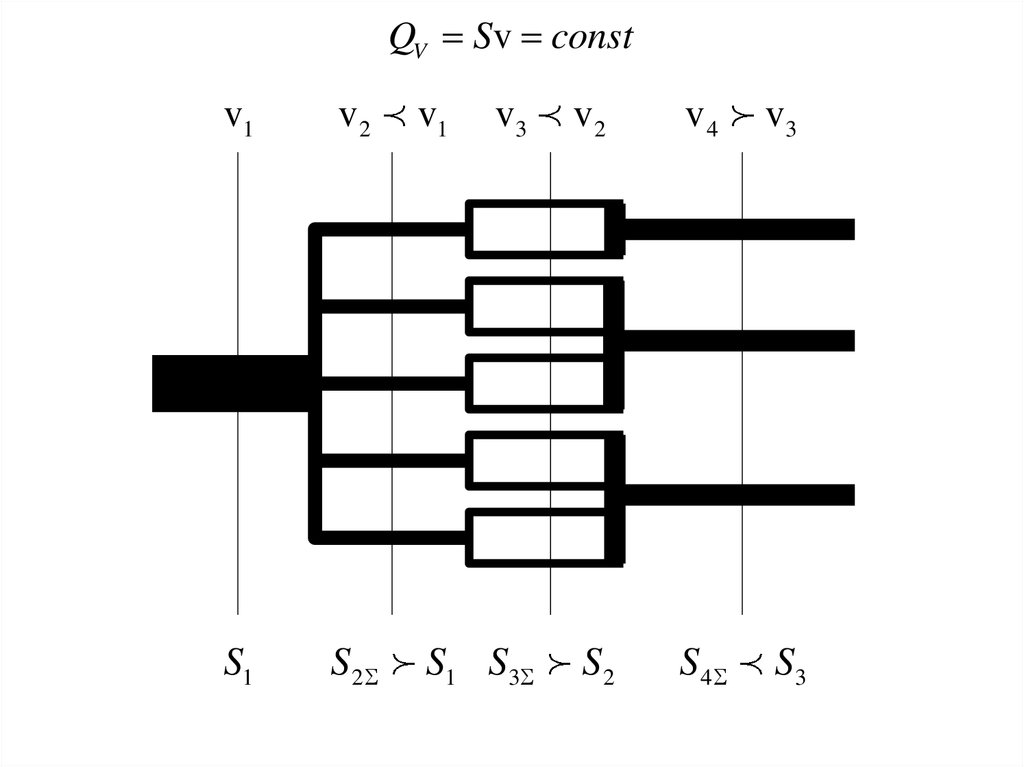
QV Sv constv1
v2
v1
v3
v2
v4
v3
S1
S2
S1 S3
S2
S4
S3
43.
3. Уравнение Бернулли для реальных жидкостейимеет качественный (неколичественный) характер:
ρv
ρv
ρgh2
p2 ρgh1
p1
2
2
2
2
2
1
Причина – потери давления на вязкое трение и на
«геометрию» канала течения
44.
4. Уравнение Пуазейля для реальных жидкостейимеет качественный (неколичественный) характер:
p1 p2 4
Q πρ
R
8ηl
R
8 l
R 4
R f ( , v, l , R)
p1 p2
Q
R
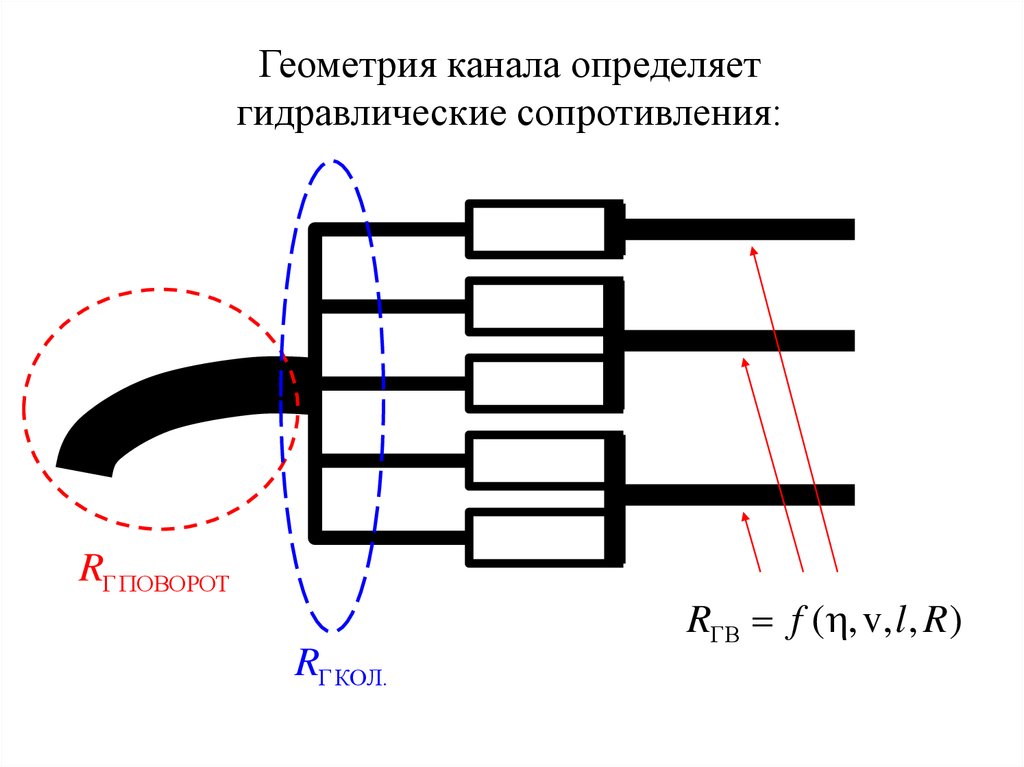
45.
Геометрия канала определяетгидравлические сопротивления:
R
R f ( , v, l , R)
RГ КОЛ.
46.
5. Перепад давления в системе в целом складываетсяиз перепадов давлений на отдельных участках:
47.
p4p1
p6
p2
p3
p8
p5
p7
p10
p9
x
48.
pp1 p2 p2 p3 pi pi 1
Q
R 12
R 23
R i ,i 1
p1
pi pi 1
p3
R i ,i 1
p5
p7
p10
1
2
3
4
5
6
7
8
9
10
x















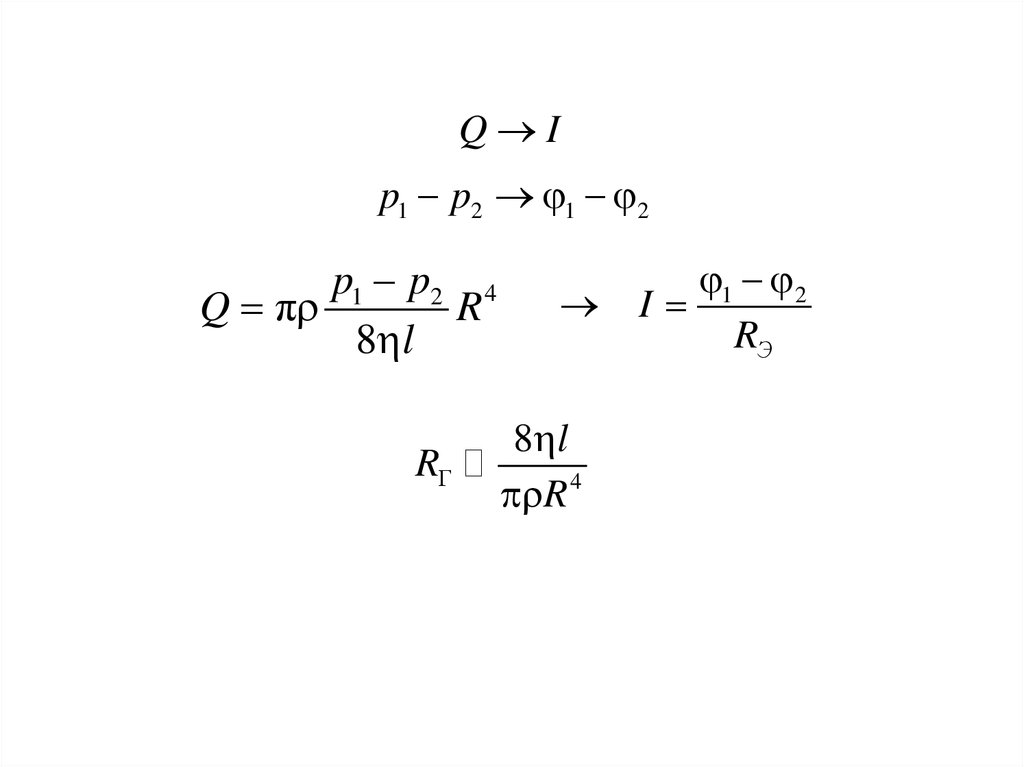












 physics
physics








