Элементы механики жидкостей и газов

1. Элементы механики жидкостей и газов

ВоГТУ
Лекция 5
Элементы механики
жидкостей и газов
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1

2. План

2

3.

Напоминание школьной программы
Давление
– это сила, действующая на единицу площади:
F
p
S
Закон Паскаля
dF
p
dS
Н
p 2 Па
м
Давление в любой точке покоящегося газа или
жидкости одинаково по всем направлениям и
одинаково передаётся по всему объёму
Гидростатическое давление
pг g h
Закон Архимеда На тело, погружённое в жидкость или газ,
действует выталкивающая сила, равная весу
вытесненной телом жидкости (газа):
FA g Vпогр.

4.

Механика жидкостей и газов
(гидроаэродинамика)
– это раздел механики,
в котором изучаются законы равновесия и
движения жидкой (и газообразной) среды и
её взаимодействия с телами, обтекаемыми
этой средой
– использует единый подход
для описания поведения жидкостей и газов
– жидкости и газы считаются несжимаемыми
– отвлекаются от молекулярного строения жидкости или газа
и рассматривают её как сплошную, непрерывную среду

5.

Способ описания в гидроаэродинамике
Частица среды – малый элемент объёма среды, размеры
которого много больше межмолекулярных
расстояний, но в то же время столь малы, что в
пределах её параметры потока (давление,
скорость течения) можно считать одинаковыми
Для описания течения жидкости задают поле скоростей
частиц жидкости, то есть зависимость скоростей
частиц
от
координат (радиус-вектора) и времени: v f (r ; t )

6.

Течение установившееся (стационарное), если:
скорость потока в данной точке не зависит от времени
Линия тока – мысленно проведённая линия, касательная к
которой в каждой точке совпадает с направлением
скорости частиц v
Трубка тока – поверхность, образованная линиями тока,
проведёнными через все точки замкнутого контура
При установившемся течении
линии тока не изменяются,
и частицы жидкости не
пересекают
поверхность
трубки тока, так как линия
тока
совпадает
с
траекторией частицы

7.

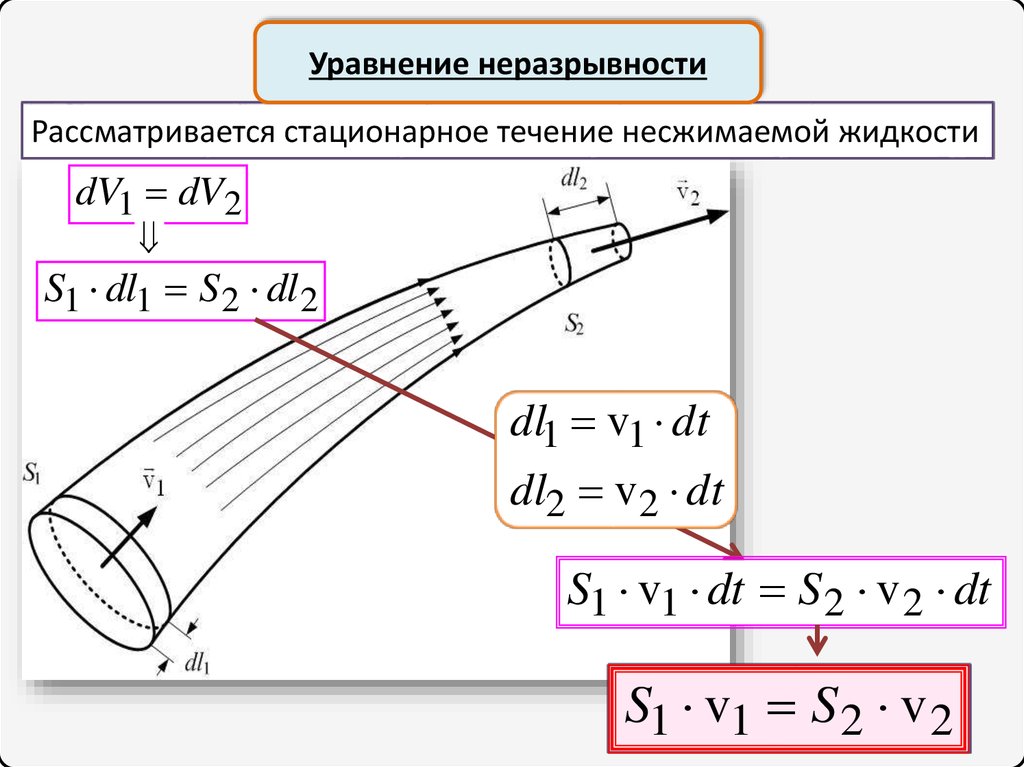
Уравнение неразрывности
Рассматривается стационарное течение несжимаемой жидкости
dV1 dV2
S1 dl1 S 2 dl 2
dl1 v1 dt
dl2 v2 dt
S1 v1 dt S 2 v 2 dt
S1 v1 S 2 v 2
7

8.

Объёмный расход
– объём, протекающий через сечение
за единицу времени:
dV S v dt
Qv
S v
dt
dt
3
Если сечения трубки тока нельзя
м
Qv
считать малыми, объёмный расход: Qv v dS
с
S
Если течение стационарно, объёмный расход в любом сечении трубки
тока одинаков – в этом смысл уравнения неразрывности
Массовый расход – масса жидкости, протекающая через
сечение за единицу времени:
dm dV
Qm
Qv
dt
dt
Qm кг
с
8

9.

Уравнение Бернулли (для идеальной жидкости)
Жидкость идеальная, если нет
внутреннего трения (вязкости)
Состояние между этими точками
не изменяется
Течение стационарно
Работа внешних сил
давления идёт только на
увеличение механической
энергии массы жидкости
dm dV
9

10.

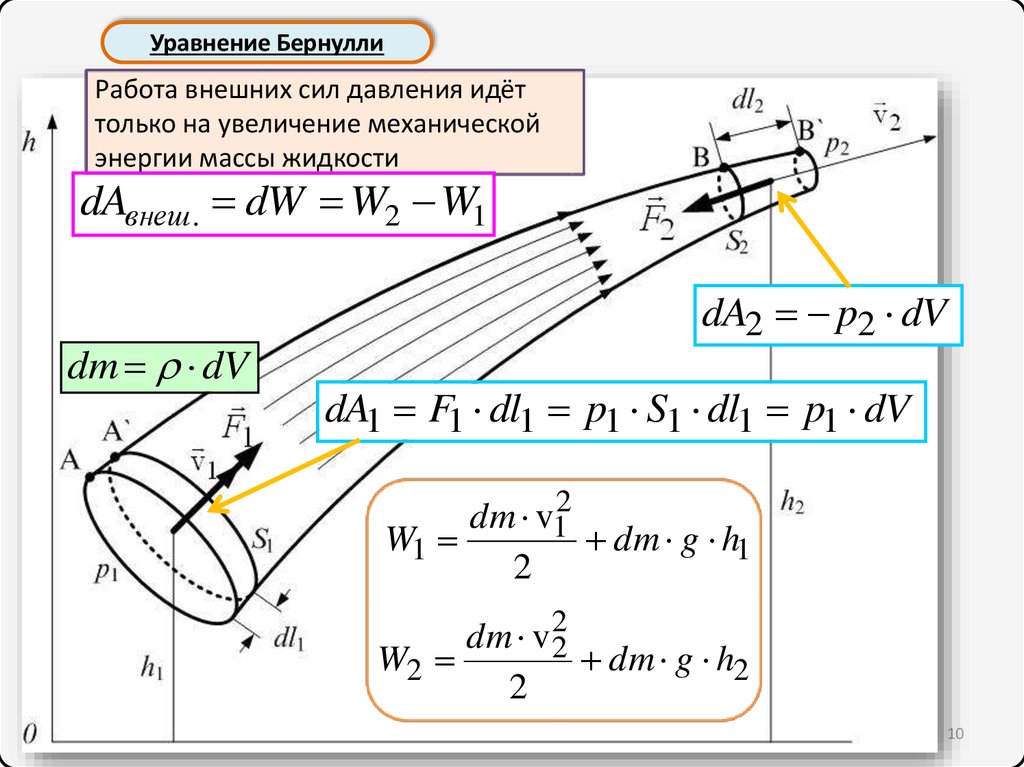
Уравнение Бернулли
Работа внешних сил давления идёт
только на увеличение механической
энергии массы жидкости
dAвнеш. dW W2 W1
dm dV
dA2 p2 dV
dA1 F1 dl1 p1 S1 dl1 p1 dV
dm v12
W1
dm g h1
2
dm v 22
W2
dm g h2
2
10

11.

Уравнение Бернулли
dAвнеш. dW W2 W1
dA1 p1 dV
dA2 p2 dV
dm v12
W1
dm g h1
2
dm v 22
W2
dm g h2
2
dAвнеш. dA1 dA2 p1 p2 dV
v 22 v12
W
W
dm
g
h
h
2
1
2
1
2
v2 v2
p1 p2 dV dm 2 1 g h2 h1
2
11

12.

Уравнение Бернулли
v2 v2
2
1
p1 p2 dV dm
g h2 h1
2
dm v 22 v12
p1 p2
g h2 h1
dV
2
dm dV
v2 v2
p1 p2 2 1 g h2 h1
2
12

13.

Уравнение Бернулли
v2 v2
2
1
p1 p2
g h2 h1
2
2
v1
p1
g h1 p2
2
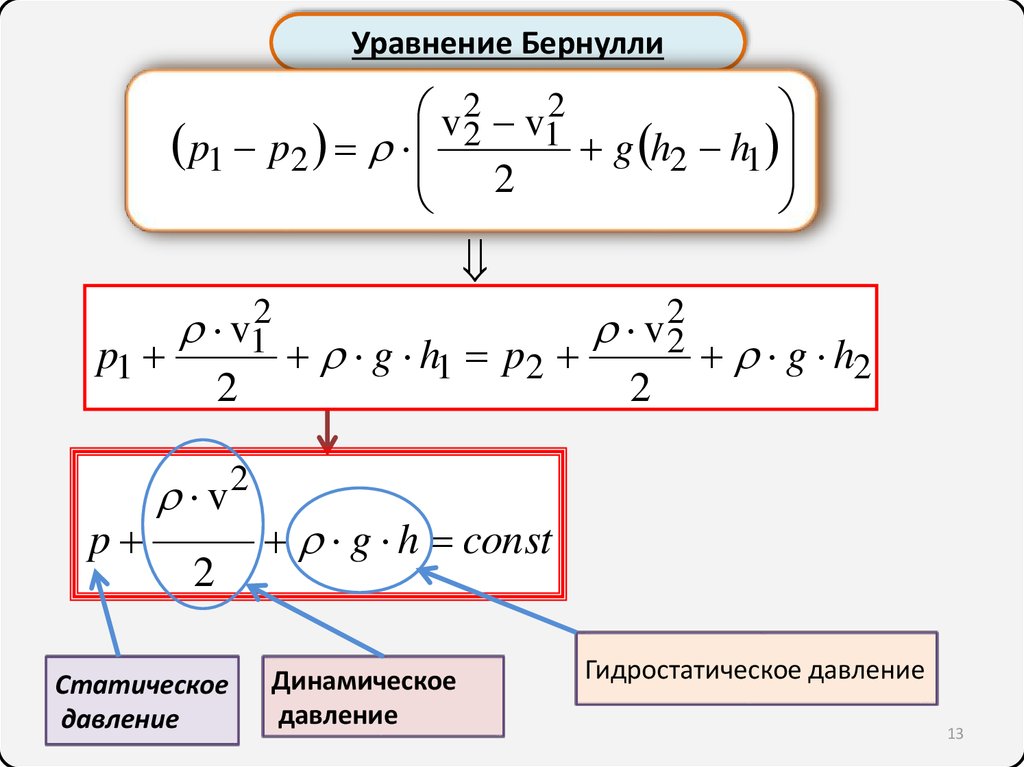
p
v2
2
Статическое
давление
2
v2
g h2
2
g h const
Динамическое
давление
Гидростатическое давление
13

14.

Уравнение Бернулли
В любом сечении трубки тока
сумма статического,
динамического
и гидростатического
давлений остаётся постоянной
p
v2
2
g h const
В горизонтальной трубе в местах сужения, где скорость
потока больше, статическое давление падает
14

15.

Примерение уравнения Бернулли
Расходомер Вентури

16.

Примерение уравнения Бернулли
Расходомер

17.

Примерение уравнения Бернулли:
Водоструйный насос

18.

Видео: шарик парит в струе воздуха
http://www.musicasenlinea.com/videos/aeeee-ae-te-;5z1uDgYjiAI.html

19.

Вязкость (внутреннее трение)
Во всех реальных жидкостях и газах при перемещении одного
слоя относительно другого возникают силы трения
Со стороны слоя, движущегося более быстро, на слой, движущийся
медленнее, действует ускоряющая сила
Со стороны слоя, движущегося медленнее, на более быстрый слой
действует тормозящая сила
Это силы внутреннего трения
Они направлены по касательной к поверхности слоёв
F
19

20.

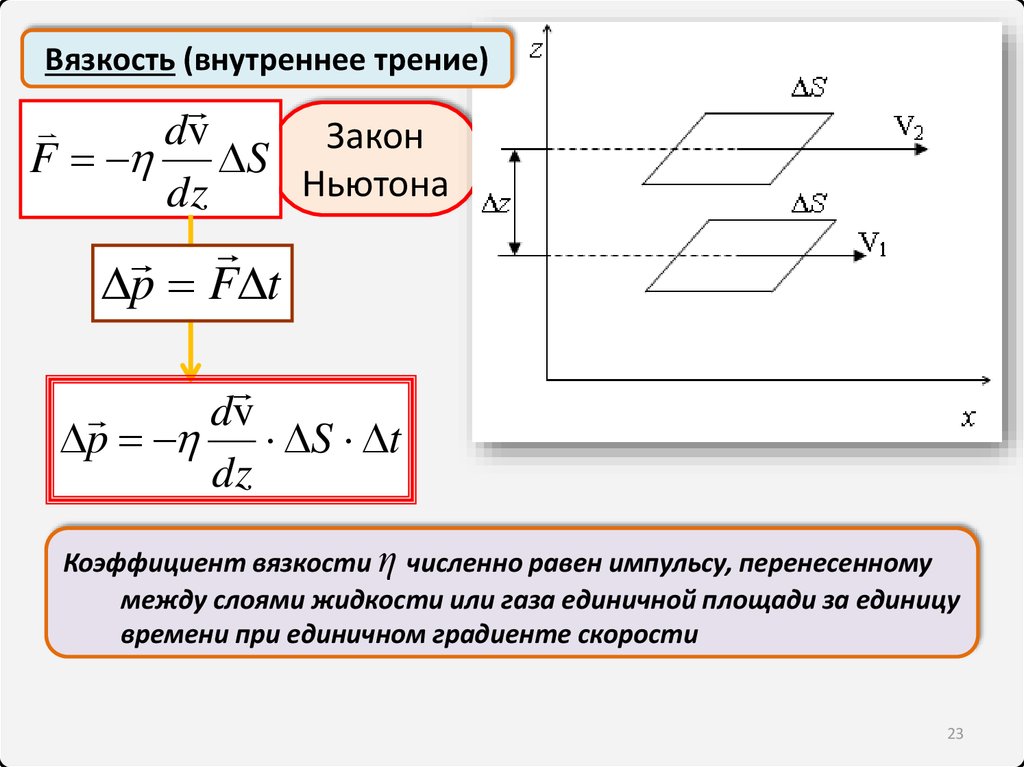
F
Вязкость (внутреннее трение)
Рассматриваются два слоя
жидкости (газа) площади ΔS,
отстоящие друг от друга на
расстояние Δz и движущиеся
перпендикулярно оси OZ с
разными скоростями
Величина силы внутреннего трения ,
действующей между слоями,
пропорциональна площади
соприкосновения движущихся слоёв и
градиенту скорости (закон Ньютона):
Закон
dv
F S
Ньютона
dz
dv
v
lim
– градиент скорости
dz z 0 z
показывает, как быстро
меняется скорость при
переходе от слоя к слою
20

21.

Вязкость (внутреннее трение)
dv
F S
dz
F
Коэффициент вязкости
(динамическая вязкость)
Па с
Знак «–» показывает, что сила направлена противоположно градиенту
скорости, то есть быстрый слой тормозится, а медленный – ускоряется
кинематическая
вязкость
Закону Ньютона не подчиняются
жидкости, состоящие из сложных и
крупных молекул, например,
растворы полимеров.
Это неньютоновские жидкости
21

22.

Вязкость (внутреннее трение)
Вязкость сильно зависит от температуры
E
Для жидкостей (по Френкелю) Aexp
kT
Здесь ΔE – энергия, которую надо сообщить
молекуле жидкости, чтобы она могла
перескочить из одного положения
равновесия в соседнее (энергия
активации)
Вязкость газов обусловлена переносом импульса из одного слоя в
другой слой, происходящим за счет переноса вещества при
хаотическом движении молекул газа
Вязкость жидкости в основном определяется силами взаимодействия
молекул между собой (силами сцепления)
22

23.

Вязкость (внутреннее трение)
dv
Закон
F S
Ньютона
dz
F
p F t
dv
p
S t
dz
Коэффициент вязкости η численно равен импульсу, перенесенному
между слоями жидкости или газа единичной площади за единицу
времени при единичном градиенте скорости
23

24.

Режимы течения
Ламинарное (слоистое)
без перемешивания слоёв
Турбулентное (вихревое) – с перемешиванием
слоёв. В отдельных точках потока скорости
отдельных частиц перпендикулярны потоку
24

25.

Число Рейнольдса
С увеличением скорости обтекания
тела ламинарное течение становится
неустойчивым, хаотичным и
переходит в турбулентное
Характер течения определяется числом Рейнольдса:
средняя скорость потока
кинематическая вязкость
Re
v D
v D
характерный размер (в случае течения
жидкости в трубе – диаметр трубы)
25

26.

Число Рейнольдса. Принцип подобия
Re
v D
v D
Re 1
Cуществует критическое число Рейнольдса, при превышении которого
происходит переход из ламинарного режима в турбулентный
Для случая течения жидкости в трубе Reкр. 10
Re<1000 Ламинарное
3
Re>1000 Турбулентное
Если для двух течений разных размеров числа Рейнольдса
одинаковы, то такие течения подобны, и возникающие в
них явления могут быть получены одно из другого
изменением масштаба
26

27.

Методы определения вязкости
1) Метод Стокса
Fc 6 r v Сила Стокса
4
3
FАрх. V ж g ж r g
3
Fтяж
4
3
mg шVg ш r g
3
По второму закону Ньютона
ma=Fтяж–FАрх–FС
Если движение установившееся, а=0
27

28.

Метод Стокса
ma=Fтяж–FАрх–FС=0
Fc 6 r v
4
FАрх. ж r 3 g
3
Fтяж
4
ш r 3 g
3
4
3
6 r v ш ж r g
3
d 2 g ш ж
18 v
28

29.

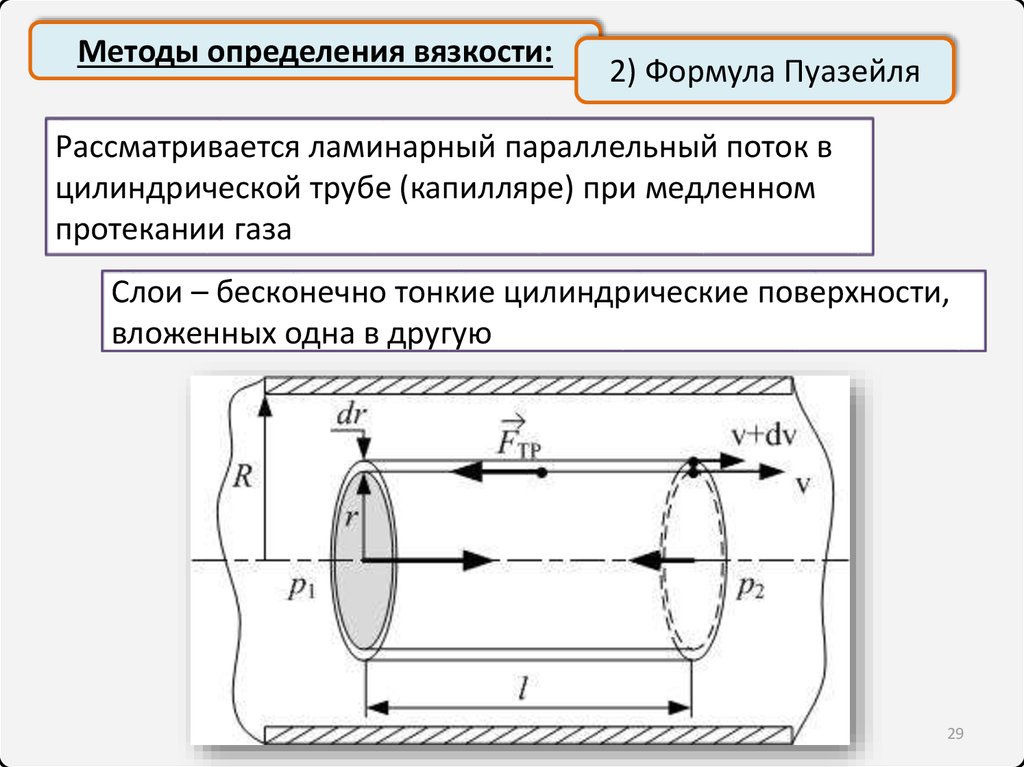
Методы определения вязкости:
2) Формула Пуазейля
Рассматривается ламинарный параллельный поток в
цилиндрической трубе (капилляре) при медленном
протекании газа
Слои – бесконечно тонкие цилиндрические поверхности,
вложенных одна в другую
29

30.

Рассматривается установившееся течение
Суммарная сила
давления на
цилиндр
уравновесится
силой вязкости:
Fд. Fвязк. 0
Fд. p1 p2 r 2
Fвязк.
dv
p1 p2 r 2 r l 0
dr
2
dv
S
dr
S 2 r l
30

31.

dv
p1 p2 r 2 r l 0
dr
2
dv
p1 p2 r
dr
2 l
p1 p2 2
v r
r C
4 l
Граничные условия:
p1 p2 2
R r 2
v r
v R 0
4 l
31

32.

Зависимость скорости частиц жидкости
от расстояния до оси капилляра
p1 p2 2
2
R r
v r
4 l
Зависимость
квадратичная
(параболическая)
32

33.

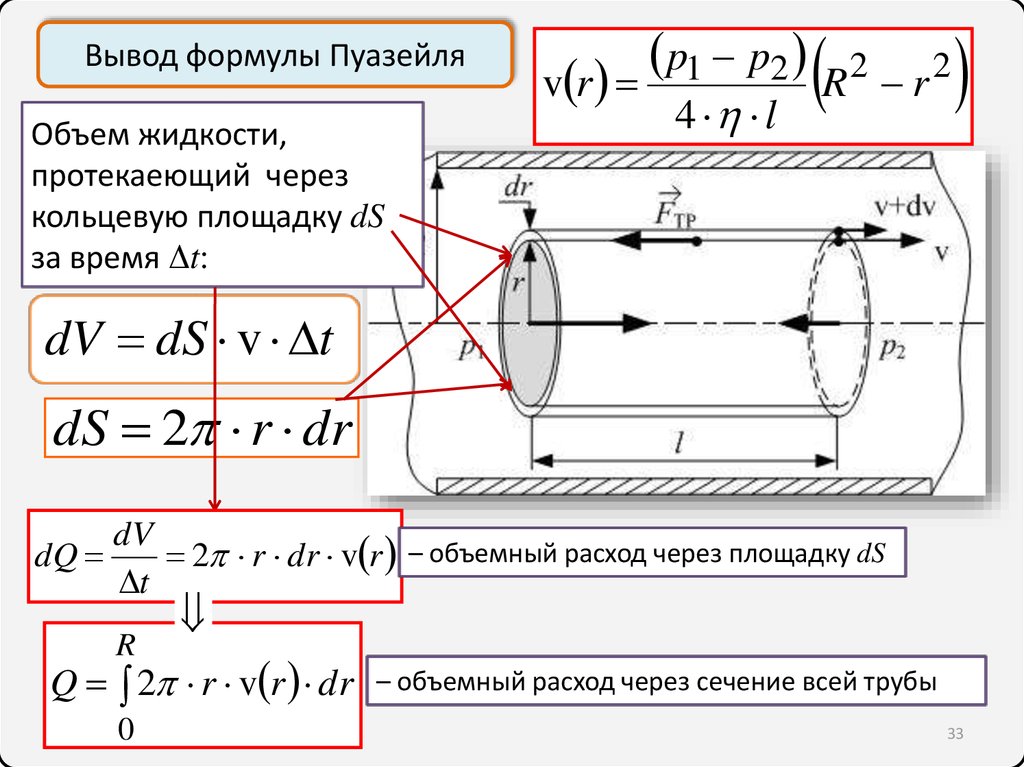
Вывод формулы Пуазейля
Объем жидкости,
протекаеющий через
кольцевую площадку dS
за время Δt:
p1 p2 2
2
R r
v r
4 l
dV dS v t
dS 2 r dr
dV
dQ
2 r dr v r – объемный расход через площадку dS
t
R
Q 2 r v r dr
0
– объемный расход через сечение всей трубы
33

34.

Вывод формулы Пуазейля
R
p1 p2 2
Q 2 r v r dr
v r
R r2
4 l
0
p1 p2 R 2
R r 2 r dr
Q 2 r v r dr
R
2 l 0
0
p1 p2 R 2
p1 p2 R
3
R r r dr
Q
2 l 0
2 l
2
2
r4
R
r
2
4
0
p1 p2 R 4 R 4
Q
2 l
2
4
34

35.

4
p1 p2 R 4 R 4
p
p
R
1
2
Q
Q
2 l 2
4
8 l
Формула Пуазейля:
p R
Q
8 l
4
Формула Пуазейля позволяет экспериментально
определить динамическую вязкость жидкости (газа),
измерив объёмный расход и зная разность давлений на
концах капилляра и его геометрические параметры
35