Магнитная гидродинамика

1. Лекция 9 Магнитная гидродинамика

Содержание
1. Общие сведения. Уравнения Максвелла, модель среды.
2. Уравнения движения проводящей жидкости в
электромагнитном поле.
3. Система уравнений магнитной гидродинамики
4. «Вмороженность» силовых линий. Диффузия магнитного
поля.
5. Волна Альфвена.

2.

Магнитная гидродинамика – часть физики плазмы со спецификой:
рассматривает движение плазменных сред с высокой проводимостью
главным образом под управляющим воздействием МП.
j E (ЭДС
Обычно в физике плазмы ток проводимости
сопоставим или меньше тока смещения
Учет МП
j
1 D
c t
|| 0
анизотропии проводимости:
и гиротропии плазмы: 1 1
e2
e2 2H
e2
e2
E)
0
H
, 3 1
, 2
2
( 2 2H )
1
ik i 2
0
i 2
1
0
0
eH
0 , H
mc
2
циклотронная частота

3.

МГД: течение хорошо проводящей жидкости (сильно нарушена
электро - нейтральность) сопровождается токам (конвективный
перенос зарядов), ток под действием МП индуцирует ЭП, оказывая
воздействие на течение.
Разные цепочки причинно-следственной связи:
Эксперимент
МГД
ЭДС
ток
Ток в МП
(течение)
МП
ЭП
МП
ток
1
E E [ v H ]
c
v 0
течение
H0
внешнее МП
Воздействие
на среду
(течение)
Формула СТО
1
E E E [H 0 v]
c
ЭП, индуцируемое током в МП

4.

Объекты МГД – движения (течения) электропроводящих жидкостей
и газов (ионизованные газы, расплавы металлов, электролиты,
магнитные суспензии) – рассматриваются на основе гипотезы
сплошности среды и непрерывного распределения заряда (тока)
Уравнения гидродинамики на основе законов электромагнетизма
обобщаются для учета воздействия электрических и магнитных
полей на течения жидкостей. В уравнениях гидродинамики
добавляются полевые по происхождению объемные силы.
Изучаемые МГД процессы
- Перекачка жидких металлов
(теплоносителей) на АЭС (МГД-насосы)
- Плазменные двигатели ракет и пушки
- Энергетика (МГД-генераторы
тока, термоядерный синтез)
- Природные явления и астрофизика
(магнитосфера Земли, проблема динамо,
процессы на Солнце)

5.

Исходные уравнения электродинамики (ЛСО)
релятивистский
1 D 4
1 B
j, rot E
,
добавок
c t
c
c t
1
div B 0, div D 4 e , j E [ v H]
c
rot H
1) В статическом состоянии для типичных сред МГД: 1, 1
Векторы индукции заменим напряженностями: В H, D E
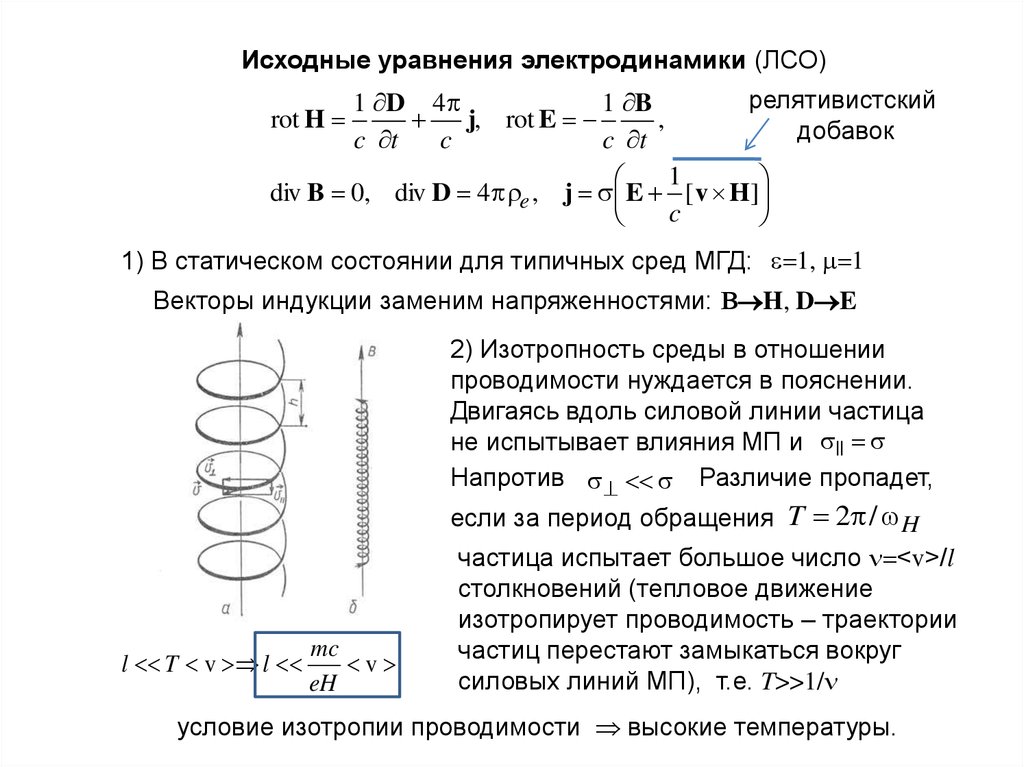
2) Изотропность среды в отношении
проводимости нуждается в пояснении.
Двигаясь вдоль силовой линии частица
не испытывает влияния МП и ||
Напротив Различие пропадет,
если за период обращения T 2 / H
l T v l
mc
v
eH
частица испытает большое число <v>/l
столкновений (тепловое движение
изотропирует проводимость – траектории
частиц перестают замыкаться вокруг
силовых линий МП), т.е. T>>1/
условие изотропии проводимости высокие температуры.

6.

3) Пренебрежение током смещения: j
1
D
E i E
t
При заданной проводимости не должны рассматриваться
быстропеременные (электромагнитные, по сути) процессы
МГД рассматривает сравнительно медленные течения
сред с достаточно хорошо выраженной проводимостью
Пренебрежение током смещения означает, что между
изменяющимися полями E и H нет запаздывания: E и H
определяют самосогласованно в один и тот же момент
времени.
В итоге, полагая в уравнениях электродинамики
D E, B H,
D
0 приходим к уравнениям Максвелла для МГД
t
rot H
4
1 H
j, rot E
,
c
c t
1
div H 0, div E 4 e , j E [ v H]
c

7.

1) Из гидродинамики (без учета вязкости) имеем уравнение Эйлера
v
p
( v ) v
f
t
Все, что добавится войдет в f результирующую плотность массовых
сил. Поэтому
f f E f H f0
f0 плотность массовых сил не электромагнитной природы
(далее опускаем)
f Е плотность массовых сил электрического поля
f Н плотность массовых сил магнитного поля
2) Из электродинамики
1
F e E [ j H ] - сила Лоренца на
c
единицу объема

8.

Приведенная к единице массы сила Лоренца
1
1
F / f E f H e E [ j H ]
c
Из уравнений Максвелла МГД имеем
e
1
c
div E, j
rot H
4
4
Для выражения по-отдельности f Е и f Н примем во внимание,
что в пренебрежении током смещения поля E и H изменяются
самосогласованно (без задержки) и величины f Е , f Н зависят от
них одинаковым образом, поддерживая симметрию по
перестановке f Е
H. В результате имеем
f Н при E
1
E div E E rot E
4
1
H div H H rot H
fH
4
fE

9.

Для последующих обобщений (например, учета сил вязкости)
следует использовать форму записи уравнения движения
жидкости, основанную на представлении объемных сил
дивергенцией тензора плотности потока импульса ik , т.е.
vi
vi ik
vk
xk xk
t
Чтобы получить ik с учетом действия сил f Е и f Н представим
эти силы в координатной форме, а затем учтем формулу
1
[ A rot A] ( A 2 ) ( A ) A
2
После несложных преобразований, получим
( f E )i
Или
1
4 xk
1 2
E
E
E ik
i k
2
( f H )i
1
4 xk
E
H
1 ik
1 ik
( f E )i
, ( f H )i
xk
xk
1 2
H
H
H ik
i k
2

10.

Величины
E
ik
1
1 2
Ei Ek E ik
4
2
H
ik
1
1 2
H
H
H ik
i k
4
2
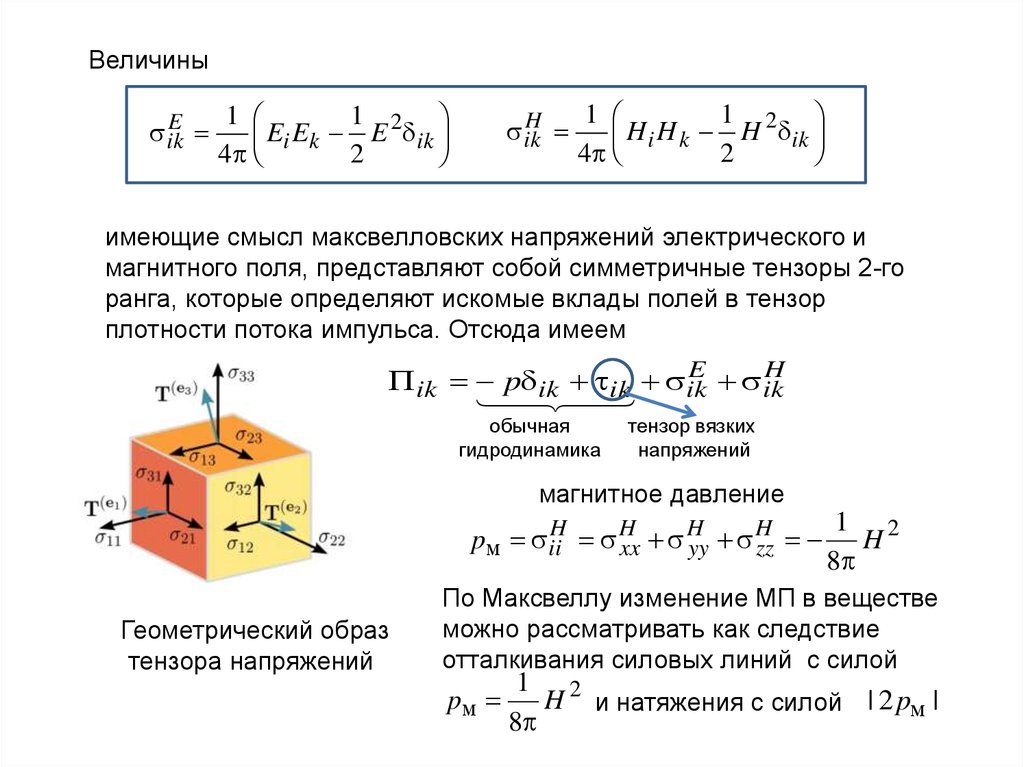
имеющие смысл максвелловских напряжений электрического и
магнитного поля, представляют собой симметричные тензоры 2-го
ранга, которые определяют искомые вклады полей в тензор
плотности потока импульса. Отсюда имеем
E
H
ik p ik ik ik
ik
обычная
гидродинамика
тензор вязких
напряжений
магнитное давление
H
H
pм iiH H
xx yy zz
Геометрический образ
тензора напряжений
1 2
H
8
По Максвеллу изменение МП в веществе
можно рассматривать как следствие
отталкивания силовых линий с силой
pм
1 2
H и натяжения с силой | 2 pм |
8

11.

Итог: магнитные силовые линии стремятся выпрямиться или
сжаться (если они замкнуты), а их распределение в веществе
стремится стать однородным из-за взаимного отталкивания.
При сильной проводимости имеет место быстрая релаксация
10
объемного заряда ( 10
с)
e 0, div E 0
Другая особенность МГД – рассматриваются достаточно
медленные процессы, когда rot E
1 H
0
c t
1
E div E E rot E 0
4
1
f 1 H rot H
fH
Hdiv
H
H
rot
H
H
4
4
0
fE
С учетом действия только этой магнитной силы уравнение
движения примет вид
v
p
1
1
( v ) v
2 v grad(div v)
[H rot H]
t
3
4

12.

Уравнение движения
v
p
1
1
( v ) v
2 v grad(div v)
[H rot H]
t
3
4
рассматривается совместно с уравнением непрерывности
div( v) 0
t
уравнением сохранения внутренней энергии u (для единицы объема)
du
dt
div
q
плотность
потока
тепла
vi
xk
( 0)
ik
плотность
потока
импульса гидродинамики
c2
(rot H) 2
16
2
плотность потока
джоулева тепла

13.

уравнениями Максвелла МГД (в пренебрежении f E )
4
1 H
rot H
j, rot E
,
c
c t
1
div H 0, div E 0, j E [ v H]
c
Всего 11 независимых уравнений для 16 неизвестных:
v, E, H, q, p, , T, u
Чтобы получилась замкнутая система уравнений добавляют:
u u ( , T ) калорическое уравнение состояния вещества
p p( , T ) термическое уравнение состояния вещества
q
T уравнение теплопроводности (закон Фурье)
t
Уравнение сохранения внутренней энергии принято описывать в
терминах вектора плотности потока энергии I. Без учета ЭЛМ-поля
имеем
I q uv v (0)
k
k
тепловой
поток
i ik
k
гидродинамический
поток

14.

Учет действия ЭП и МП
Из электродинамики
S
I I S
c
[E H ] вектор Пойтинга
4
С учетом уравнения баланса мощности для ЭЛМ-поля
w
1
j E div S, w
( E 2 H 2 ) плотность энергии
t
8
ЭЛМ-поля
после добавления в уравнении сохранения энергии w к u получим
закон сохранения полной энергии среды в виде
d
( u w) div I, I k qk v k u vi ik S k
dt
1
j E [ v H ]
c
c
1
E
rot H [ v H]
4
c
В уравнениях Максвелла МГД подставим
в уравнение rot H
4
j
c
уравнение для определения ЭП

15.

E
c
1
rot H [ v H]
4
c
1 H
с
c t 4
rot E
rot(rot H)
2
grad(div
H
)
H
1 H
c t
1
rot[ v H]
c
0
H с 2 2
H rot[ v H]
t 4
Уравнение для
определения МП
Сводная система уравнений МГД
v
p
1
1
( v ) v
2 v grad(div v)
[H rot H]
t
3
4
H с 2 2
H rot[ v H]
t 4
E
c
1
rot H [ v H]
4
c

16.

Граничные условия:
Неподвижная твердая граница v s 0 условие прилипания
На границе тела, движущегося со скоростью U
На свободной границе ( p pM ) s 0,
pM
v s U
1 2
H
8
магнитное
давление
На границе раздела жидкостей – непрерывность скоростей
и давлений
К гидродинамическим ГУ добавляются ГУ электродинамики:
E (1) s E ( 2) s , H n(1) s H n( 2) s , H (1) s H ( 2) s
j s плотность поверхностного тока
4
js
c

17.

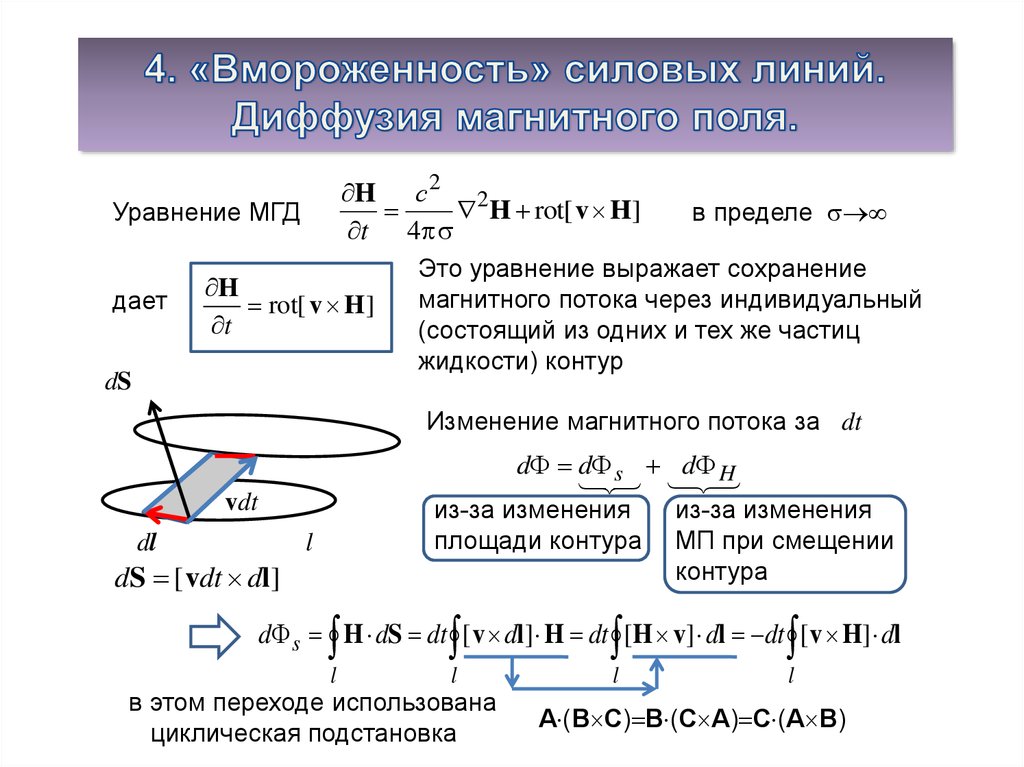
H с 2 2
H rot[ v H]
Уравнение МГД
в пределе
t 4
Это уравнение выражает сохранение
H
магнитного потока через индивидуальный
дает
rot[ v H ]
t
(состоящий из одних и тех же частиц
жидкости) контур
dS
Изменение магнитного потока за dt
d d s d H
из-за изменения
из-за изменения
площади контура МП при смещении
контура
vdt
dl
l
dS [ vdt dl ]
l
l
l
l
d s H dS dt [ v dl] H dt [H v] dl dt [ v H] dl
в этом переходе использована
циклическая подстановка
A (B C) B (C A) C (A B)

18.

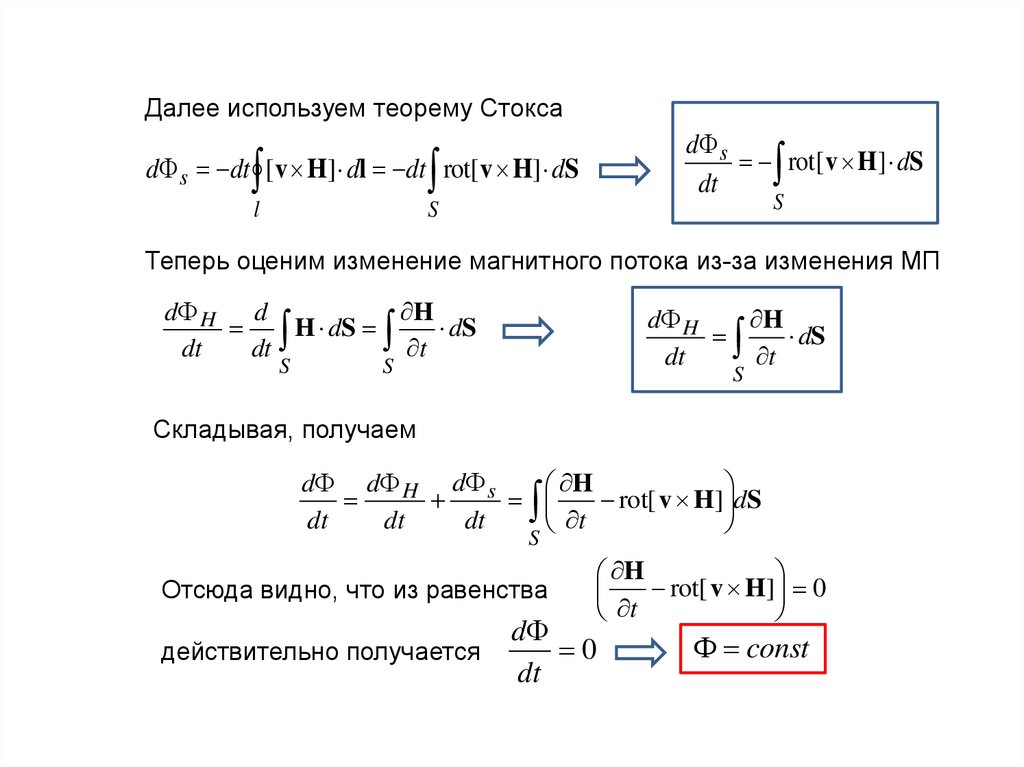
Далее используем теорему Стокса
l
S
d s
rot[ v H] dS
dt
d s dt [ v H] dl dt rot[ v H] dS
S
Теперь оценим изменение магнитного потока из-за изменения МП
d H d
H
H dS
dS
dt
dt
t
S
S
d H
H
dS
dt
t
S
Складывая, получаем
d d H d s
H
rot[ v H] dS
dt
dt
dt
t
S
Отсюда видно, что из равенства
действительно получается
H
rot[ v H ] 0
t
d
0
dt
const

19.

Постоянство S означает
- при сжатии контура силовые линии сближаются, МП возрастает
- при расширении индивидуального сверхпроводящего контура
силовые линии МП разбегаются – напряженность поля падает.
Иначе это можно связать с тем, что при движении (течении)
сверхпроводящей жидкости поперек МП вместе с ней
перемещается и само магнитное поле – линии МП как бы
«вморожены» в жидкость.
Следствие «вмороженности» теорема Валена:
Если индивидуальные частицы идеально
проводящей жидкости в некоторый начальный
момент времени находились на одной силовой
линии МП, то они останутся на ней во все
последующие моменты времени
Индивидуальные частицы жидкости не могут
пересекать магнитные силовые линии, которые, в свою очередь,
не могут опережать или отставать от движущихся частиц.

20.

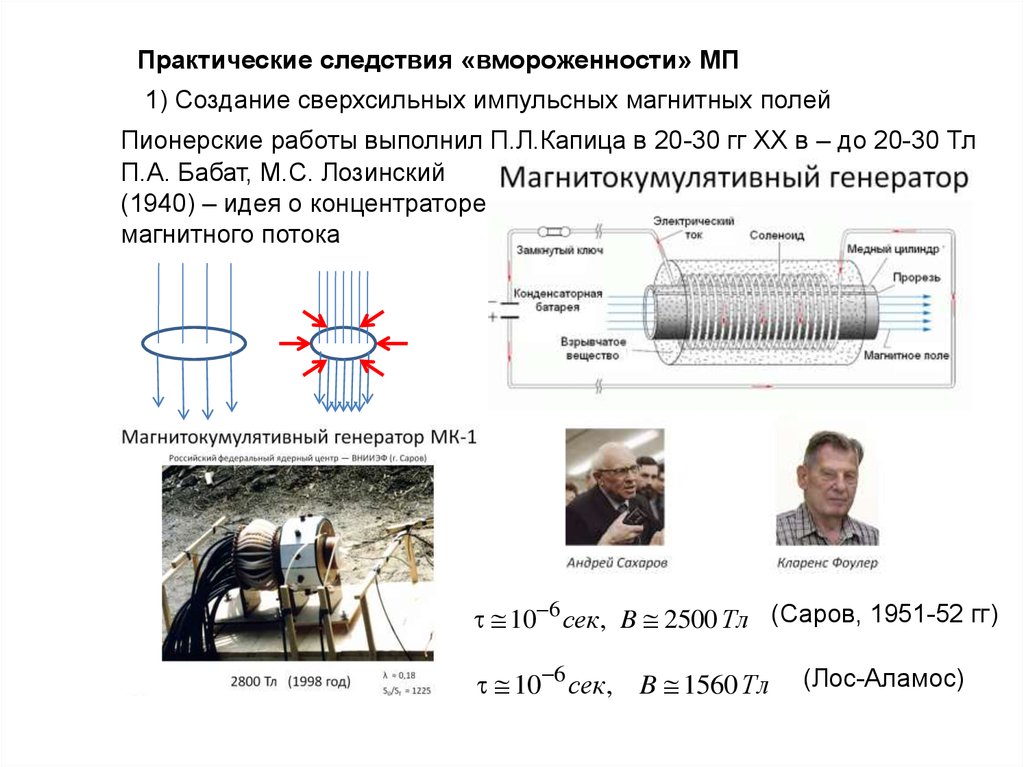
Практические следствия «вмороженности» МП
1) Создание сверхсильных импульсных магнитных полей
Пионерские работы выполнил П.Л.Капица в 20-30 гг ХХ в – до 20-30 Тл
П.А. Бабат, М.С. Лозинский
(1940) – идея о концентраторе
магнитного потока
10 6 сек, B 2500 Тл (Саров, 1951-52 гг)
10 6 сек, B 1560 Тл
(Лос-Аламос)

21.

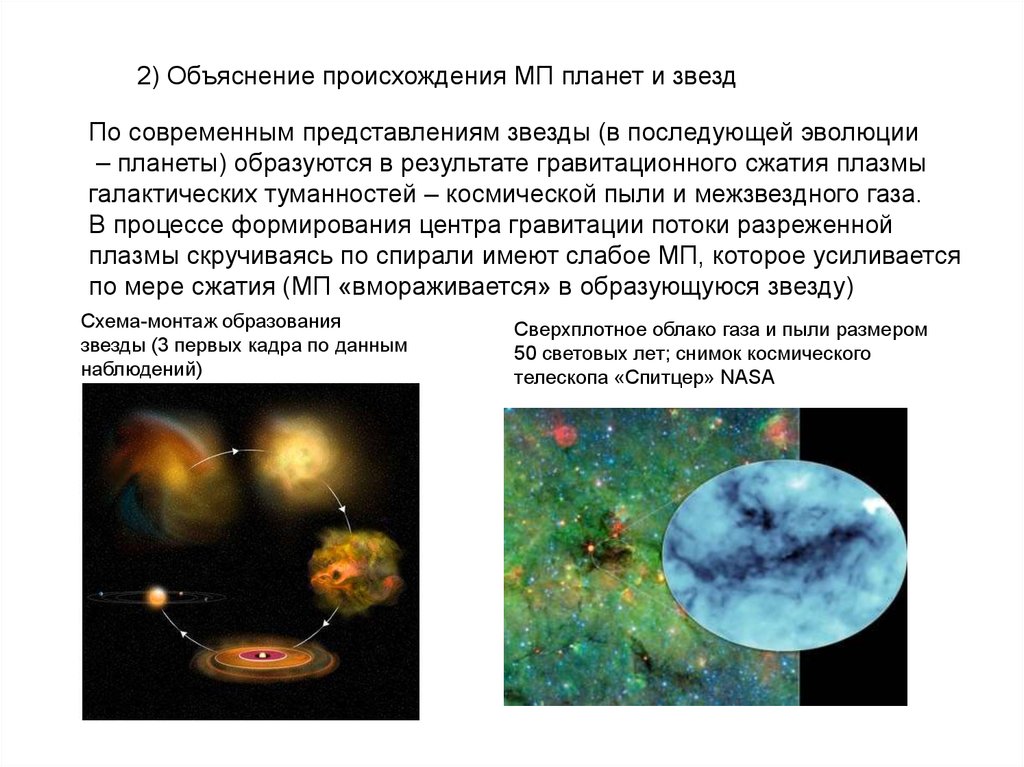
2) Объяснение происхождения МП планет и звезд
По современным представлениям звезды (в последующей эволюции
– планеты) образуются в результате гравитационного сжатия плазмы
галактических туманностей – космической пыли и межзвездного газа.
В процессе формирования центра гравитации потоки разреженной
плазмы скручиваясь по спирали имеют слабое МП, которое усиливается
по мере сжатия (МП «вмораживается» в образующуюся звезду)
Схема-монтаж образования
звезды (3 первых кадра по данным
наблюдений)
Сверхплотное облако газа и пыли размером
50 световых лет; снимок космического
телескопа «Спитцер» NASA

22.

3) Диффузия МП
«Вмороженность» МП – в чистом виде имеет место только в средах
с (т.е. в сверхпроводниках). Среды с конечной проводимостью
проницаемы для МП – МП будет «диффундировать» в них.
В случае предельно медленных течений v 0 уравнение для МП
H с 2 2
H rot[ v H]
t 4
x
H с 2 2
H,
t 4
0
H0
z
S
Задача аналогична задаче
Рэлея о приведение в
движение вязкой жидкости
плавающей пластиной
с2
DM
4
Уравнение аналогично уравнению
диффузии или теплопроводности
( DM коэффициент магнитной
диффузии)
Рассмотрим задачу о диффузии МП
из вакуума в плазменное
полупространство. Изначально поле
экранируется от плазмы экраном S ,
который в момент t 0 внезапно
убирают.

23.

Так как H 0 || z , возникающее в плазме (x 0) МП H также будет || z .
Поле H 0 не зависит от z
H (0,0, H z ), H z H z ( x, t )
Уравнение для поля
H
DM 2 H
t
решаем при начальном условии
и граничных условиях
H z ( x,0) 0, 0 x
0, t 0
H z (0, t )
H 0 , t 0
H z ( x, t ) x 0
В данных условиях задача является одной из ключевых задач
математической физики с известным решением вида
x
H z ( x, t ) H 0 1 erf
4 D t
M
интеграл вероятностей
w
2
2
erf( w)
e d
0

24.

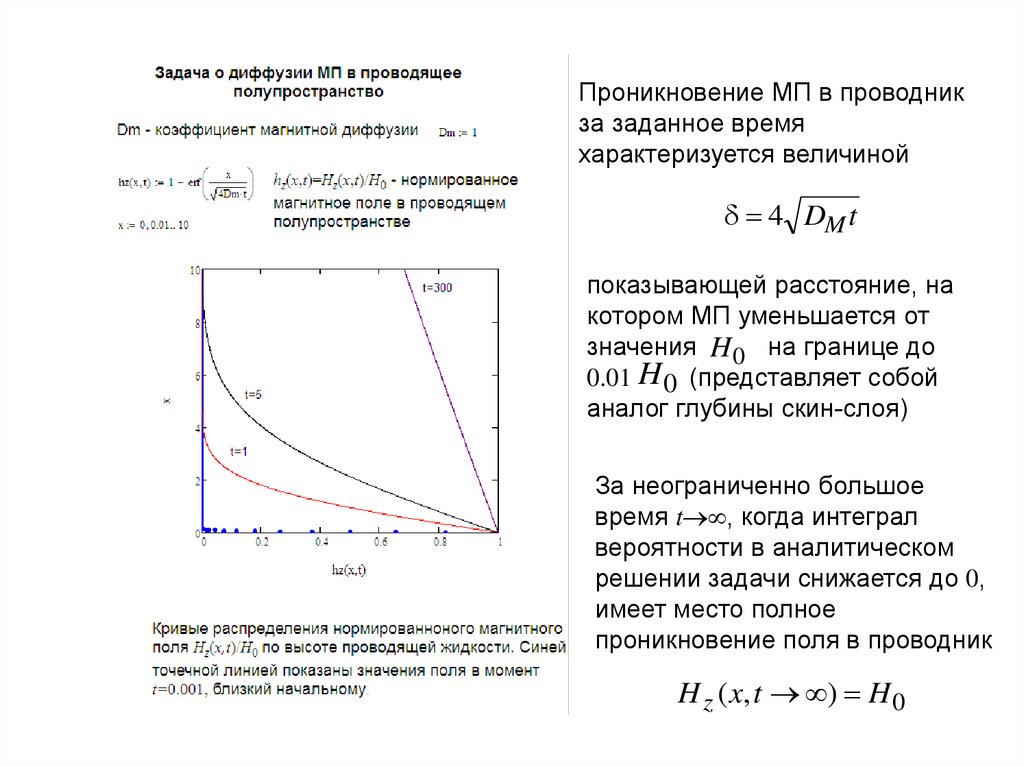
Проникновение МП в проводник
за заданное время
характеризуется величиной
4 DM t
показывающей расстояние, на
котором МП уменьшается от
значения H 0 на границе до
0.01 H 0 (представляет собой
аналог глубины скин-слоя)
За неограниченно большое
время t , когда интеграл
вероятности в аналитическом
решении задачи снижается до 0,
имеет место полное
проникновение поля в проводник
H z ( x, t ) H 0

25.

Шведский физик Альфвéн Ханнес – лауреат
нобелевской премии (1970) за работы в области
магнитной гидродинамики.
Показал, что в магнитном поле
в жидкости
может существовать особый тип чисто поперечной
магнито-гидродинамической волны. Жидкости не
обладают сдвиговой упругостью – сопротивлением
формы. Поэтому, обычно, поперечные волны в
них не существуют.
«Сдвиговая упругость» проводящей жидкости в МП проявляется за счет
эффекта вмороженности силовых линий.
z
v, h || z
H0
возвращающая сила натяжения
силовых линий МП
x

26.

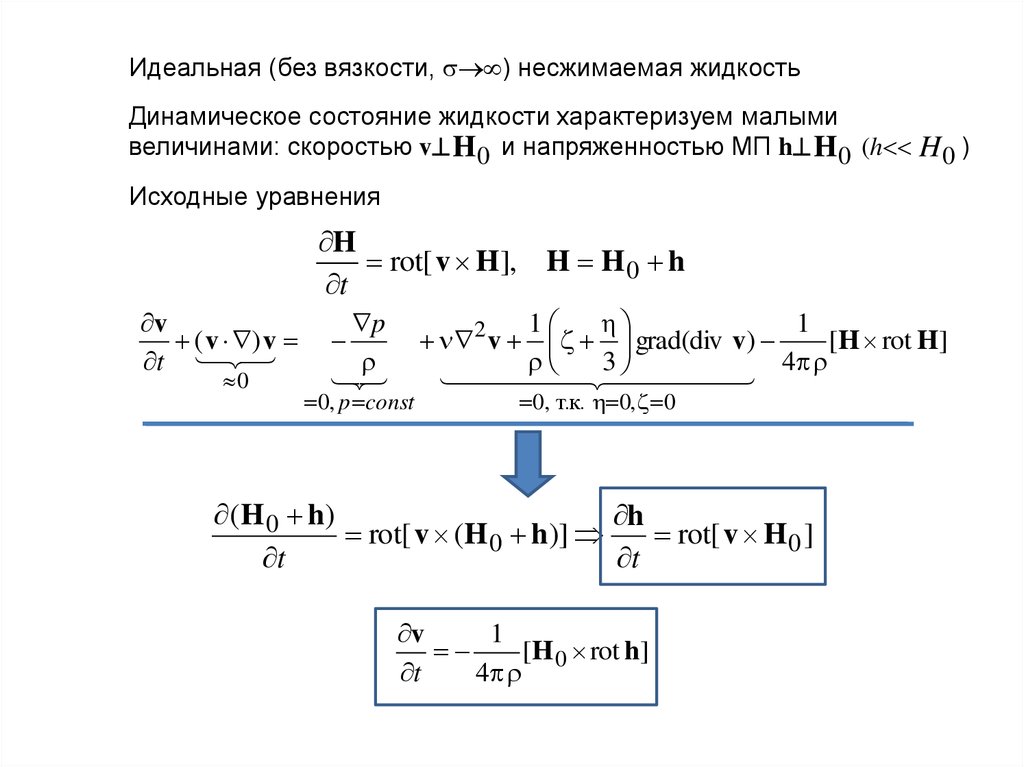
Идеальная (без вязкости, ) несжимаемая жидкость
Динамическое состояние жидкости характеризуем малыми
величинами: скоростью v H 0 и напряженностью МП h H 0 (h H 0 )
Исходные уравнения
H
rot[ v H ], H H 0 h
t
v
( v ) v
t
0
p
0, p const
1
1
2 v grad(div v)
[H rot H]
3
4
0, т.к. 0, 0
(H 0 h)
h
rot[ v (H 0 h)]
rot[ v H 0 ]
t
t
v
1
[H 0 rot h]
t
4

27.

Так как имеем векторы
v i 0 j 0 k v( x, t ), h i 0 j 0 k h( x, t ), H0 i H 0 j 0 k 0
получаем
i
[v H0 ] 0
H0
i
rot[ v H 0 ]
x
0
j
k
0 v(x, t) j v( x, t ) H 0
0
0
j
k
0
0 kH 0
v( x,t) H 0
0
h
h( x, t )
v( x, t )
rot[ v H 0 ]
H0
t
t
x
(I)
v( x, t )
t

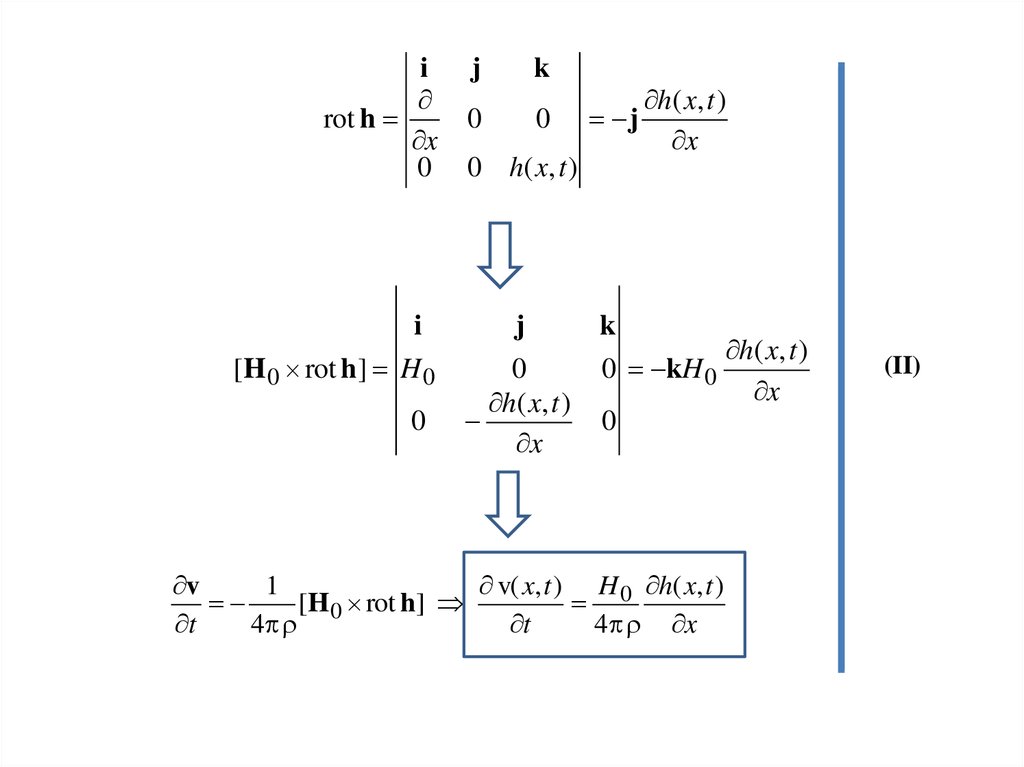
28.

i
rot h
x
0
i
[H 0 rot h] H 0
0
j
k
0
0
j
h( x, t )
x
0 h ( x, t )
j
0
h( x, t )
x
k
0 kH 0
0
v
1
v( x, t ) H 0 h( x, t )
[H 0 rot h]
t
4
t
4 x
h( x, t )
x
(II)

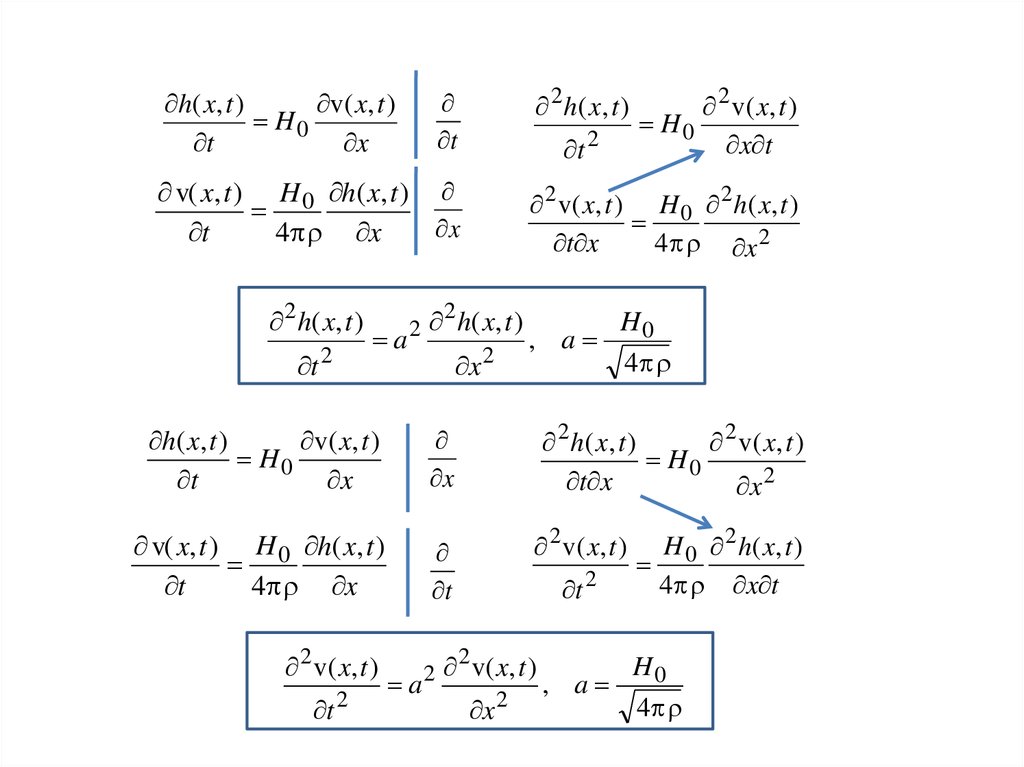
29.

h( x, t )
v( x, t )
H0
t
x
t
2 h ( x, t )
t 2
v( x, t ) H 0 h( x, t )
x
t
4 x
2 h( x, t )
t 2
a
2
x 2
x
v( x, t ) H 0 h( x, t )
t
4 x
t
2 v ( x, t )
t 2
a
2 v ( x, t ) H 0 2 h ( x, t )
t x
4 x 2
2 h ( x, t )
h( x, t )
v( x, t )
H0
t
x
2
2 v ( x, t )
H0
x t
, a
H0
4
2 h ( x, t )
2 v ( x, t )
H0
t x
x 2
2 v ( x, t )
t 2
2 v ( x, t )
x 2
, a
H 0 2 h ( x, t )
4 x t
H0
4

30.

Поперечные к постоянному МП динамические МП h и скорость v
удовлетворяют одному и тому же волновому уравнению и описывают
поперечную МГД-волну Альфвена, распространяющуюся с
постоянной скоростью
a
H0
4
В случае идеальной жидкости (плазмы) волна Альфвена не имеет
частотной дисперсии. При учете вязкости и конечной проводимости
она становится дисперсивной и затухающей.
Произвольное распространение плоских волн Альфвена по
отношению к внешнему МП
h
rot v H 0
t
2h
v
rot H 0
t
t 2
v
1
1
H 0 rot h
rot h H 0
t
4
4

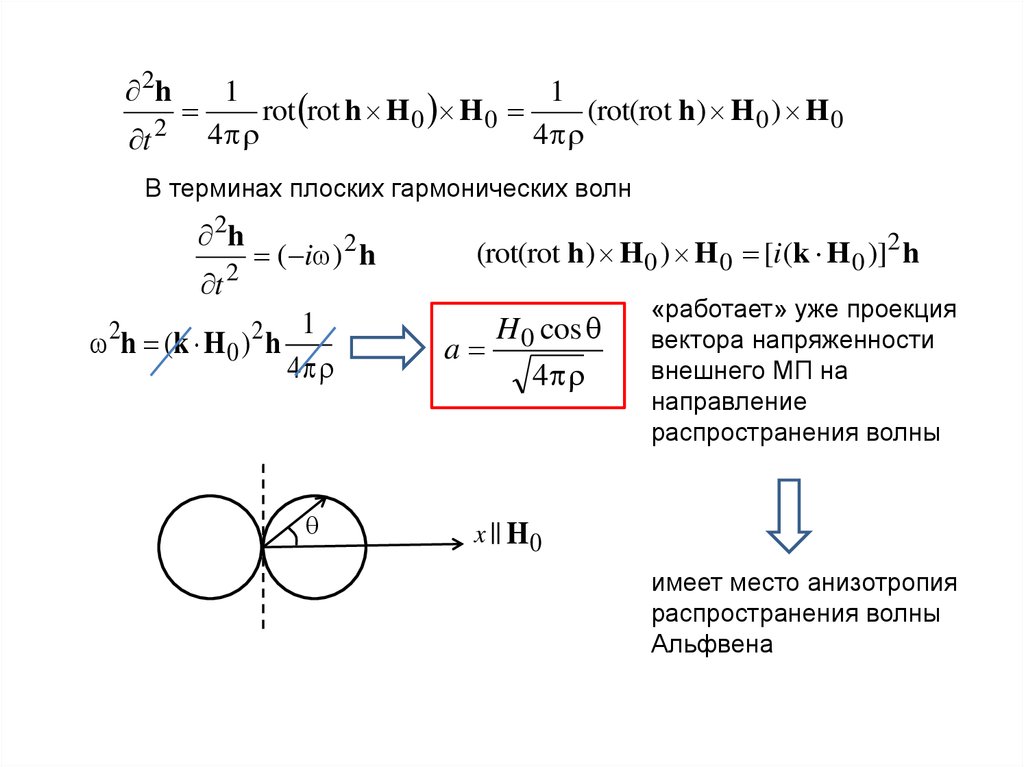
31.

2h
t 2
1
1
rot rot h H 0 H 0
(rot(rot h) H 0 ) H 0
4
4
В терминах плоских гармонических волн
2h
(rot(rot h) H 0 ) H 0 [i (k H 0 )]2 h
( i ) 2 h
t 2
«работает» уже проекция
1
H 0 cos
вектора напряженности
2h (k H 0 ) 2 h
a
4
внешнего МП на
4
направление
распространения волны
x || H 0
имеет место анизотропия
распространения волны
Альфвена