Similar presentations:
Уравнения Максвелла
1. Литература
2. Уравнения Максвелла
1873 г.Материальные уравнения
B
rot E
t
D 0 E
B 0 H
D
rot H j
t
j E
div D
Параметр
Тип среды
div B 0
=0
Диэлектрическая
0
Проводящая
= const
Однородная, изотропная
= (x, y, z)
Неоднородная
= (направления)
Анизотропная
= (E)
Нелинейная
© К.К.Боярский 2010
3. Граничные условия
E 1 E 2H 1 H 2
Dn1 Dn 2
Bn1 Bn 2
© К.К.Боярский 2010
4. Волновое уравнение
Однородный изотропныйдиэлектрик
H
rot E 0
t
E
rot H 0
t
t
div E 0
div H 0
© К.К.Боярский 2010
2 E
rot rot E 0 0 2
t
rot rot E grad divE E
Оператор Лапласа
2
2
2
2 2 2
x
y
z
2 E
E 0 0 2
t
5. Скорость э/м волн
2 EE 0 0 2
t
Вакуум: c
1 2 E
E 2 2
v t
1
0 0
v
c 299792456 ì ñ
c
Показатель преломления n
v
Вещество
n
Вещество
n
n
водород
1,000139 1,000139 бензол
1,501 1,511
воздух
1,000292 1,000302 спирт
1,36
5,1
1,33
9
углекислота 1,000499 1,000485 вода
© К.К.Боярский 2010
1
0 0
6. Плоская монохроматическая волна
E E ( z)2 E
1 2 E
2 2
2
z
v t
z
z
E( z, t ) A1 cos t A2 cos t
v
v
2 v
vT
© К.К.Боярский 2010
Плоская волна:
волновой фронт z = const
7. Шкала э/м волн
© К.К.Боярский 2010
8. Формы уравнения плоской волны
zE( z, t ) A cos t
v
E( z, t ) A cos t kz
2
k
v
волновое число
1
k
см
E( r , t ) A cos t k r
k nk
волновой вектор
E( r , t ) Ae
i t kr
© К.К.Боярский 2010
9. Сферические волны
A1A2
E( r, t )
cos t kr
cos t kr
r
r
© К.К.Боярский 2010
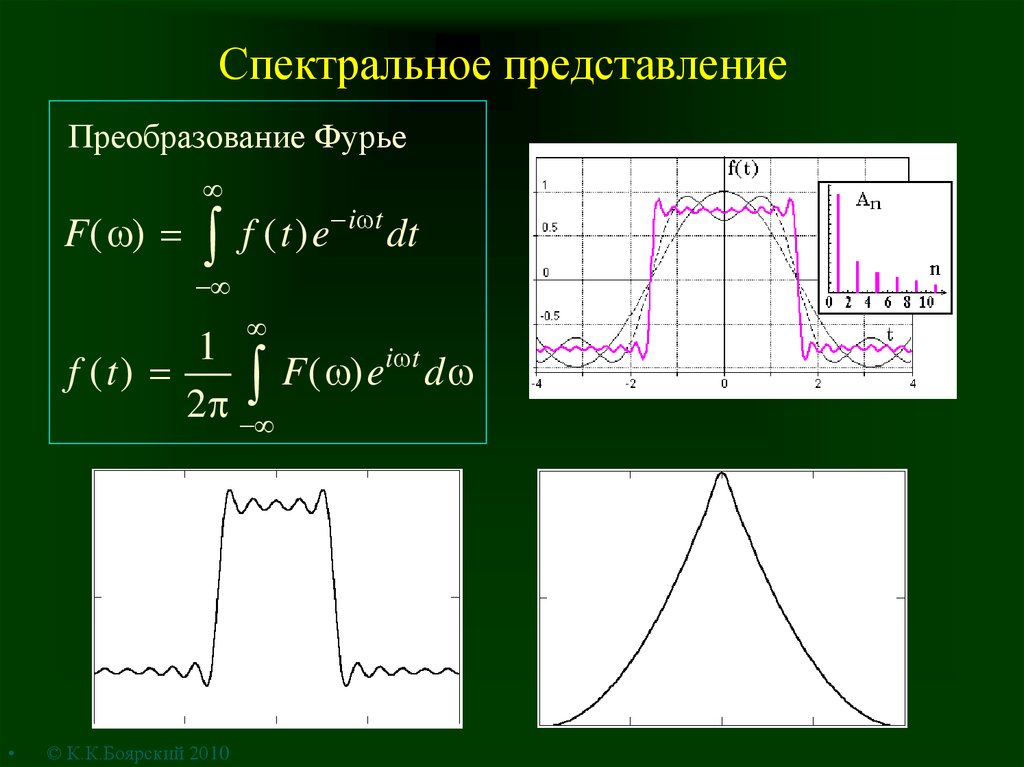
10. Спектральное представление
Преобразование ФурьеF( )
f ( t ) e i t dt
1
i t
f (t)
F
(
)
e
d
2
© К.К.Боярский 2010
11. Свойства э/м волн
E( x , y , z, t ) Aei t kr
E
i E
t
Aei t k x k y k z
E
ikx E
x
H
rot E 0
t
E
rot H 0
t
x
y
z
E ik E
ik E 0 i H
ik H 0 i E
E, H , k
E k,
H k
Поперечность
© К.К.Боярский 2010
Правая
тройка
векторов
12. Интенсивность света
kE 0 H 0 E 0 HВектор Пойнтинга – вектор
плотности потока энергии
E E0 cos t kr
H H 0 cos t kr
I S
© К.К.Боярский 2010
E02
S E H
S
[ I ] = Вт/м2
0 2
nE0 cos2 t kr
0
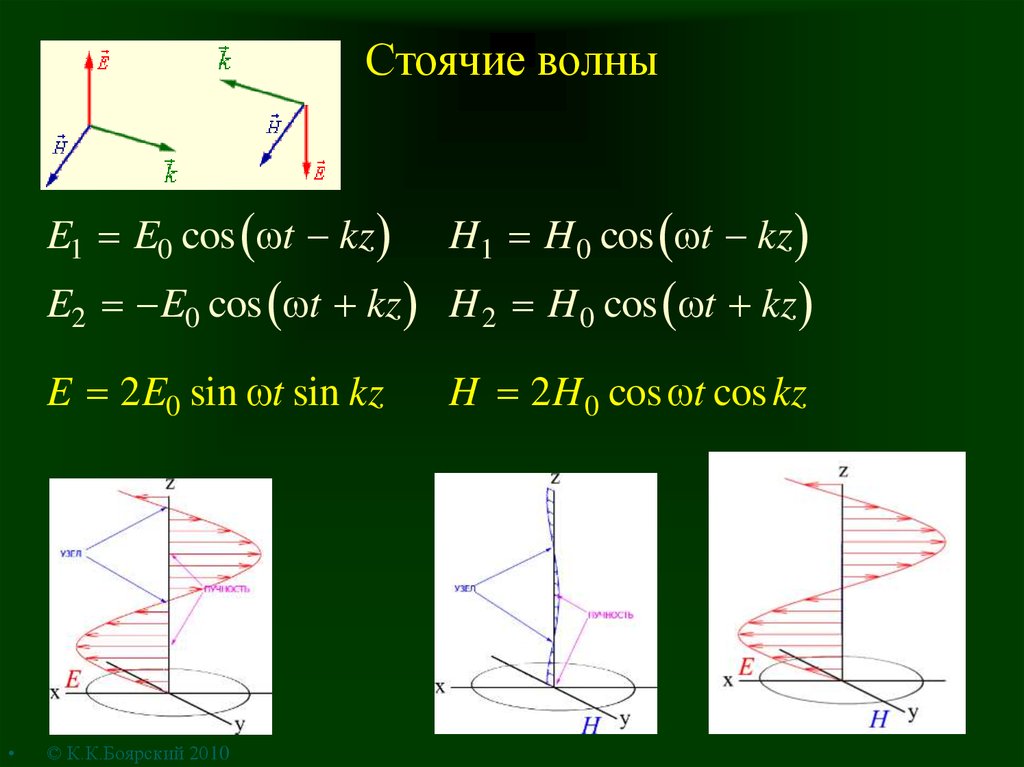
13. Стоячие волны
E1 E0 cos t kzH1 H 0 cos t kz
E2 E0 cos t kz H 2 H 0 cos t kz
E 2E0 sin t sin kz
© К.К.Боярский 2010
H 2H 0 cos t cos kz
14. Опыт Винера
E cBFì àãí
evB
Fýë
eE
1890 г.
© К.К.Боярский 2010
v
c












 physics
physics








