Энергия поля в среде

1.

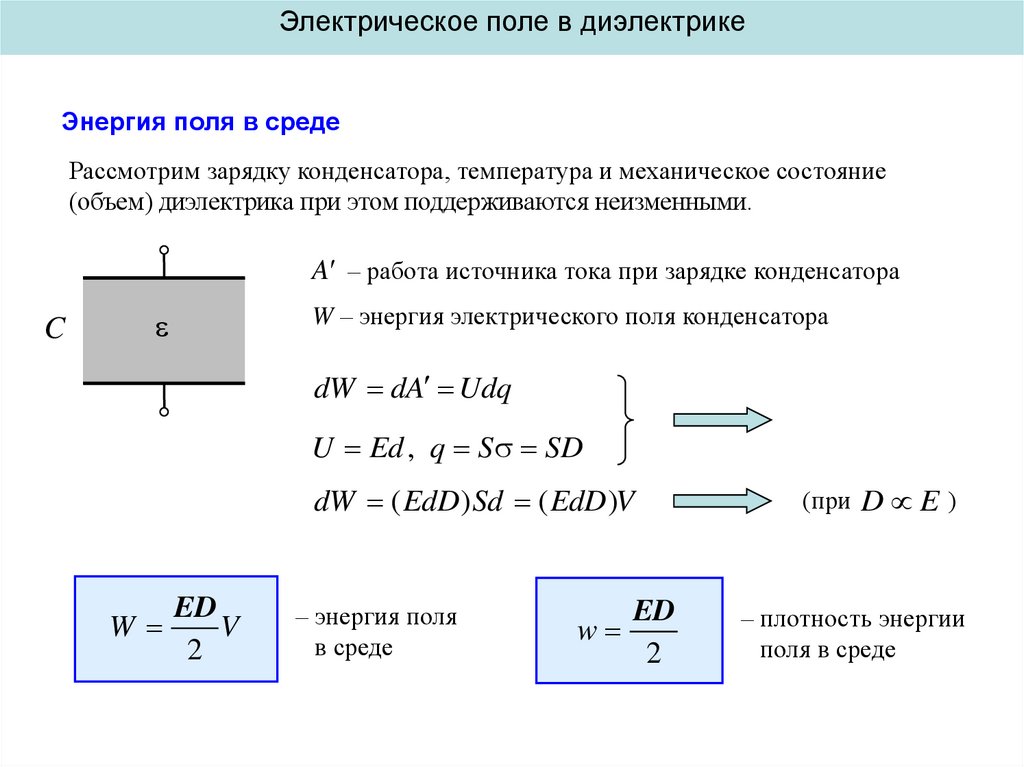
Электрическое поле в диэлектрике
Энергия поля в среде
Рассмотрим зарядку конденсатора, температура и механическое состояние
(объем) диэлектрика при этом поддерживаются неизменными.
A – работа источника тока при зарядке конденсатора
C
W – энергия электрического поля конденсатора
dW dA Udq
U Ed , q S SD
dW ( EdD ) Sd ( EdD )V
W
ED
V
2
– энергия поля
в среде
ED
w
2
(при D E )
– плотность энергии
поля в среде

2.

Постоянный электрический ток
Сила и плотность тока
Электрический ток – упорядоченное движение электрических зарядов.
dQ – заряд, прошедший через поверхность S за dt
dQ
dQ
I
dt
j u
– сила тока
– плотность тока
– объемная плотность заряда, u – скорость его носителя
dQ
u
udt
dQ udt dS
dI udS jdS
dS
I j dS
S

3.

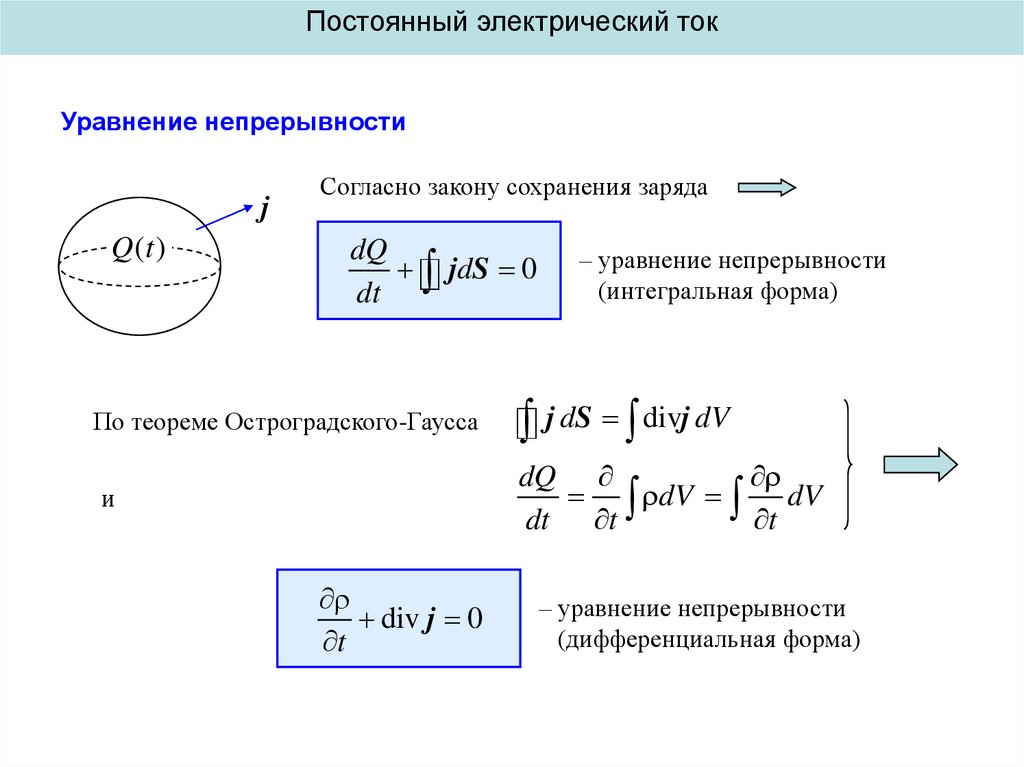
Постоянный электрический ток
Уравнение непрерывности
j
Q (t )
Согласно закону сохранения заряда
dQ
dt
jdS 0
По теореме Остроградского-Гаусса
– уравнение непрерывности
(интегральная форма)
j dS divj dV
dQ
dV dV
dt t
t
и
div j 0
t
– уравнение непрерывности
(дифференциальная форма)

4.

Постоянный электрический ток
Закон Ома для однородного участка цепи
R
Для металлических проводников и др.
j E
– закон Ома для однородного участка цепи
(локальная форма)
– удельная проводимость,
1
– удельное сопротивление

5.

Постоянный электрический ток
Закон Ома для однородного участка цепи
Длинный тонкий проводник (S = const)
l
2
S
x
I
const
S
U 1 2 El
j
E ( x ) E const
1
j E
U RI
I 1U
S l
– закон Ома для однородного участка цепи
(интегральная форма)
Для длинного тонкого проводника
l
R
S

6.

Постоянный электрический ток
Закон Ома для неоднородного участка цепи
Причина существования постоянного тока –
наличие сторонних электродвижущих сил не электростатической природы.
F
E
q
R
– напряженность поля сторонних сил
j ( E E )
– закон Ома для
неоднородного участка цепи
(локальная форма)

7.

Постоянный электрический ток
Закон Ома для неоднородного участка цепи
Длинный тонкий проводник
2
1
2
1
1
1
I
1 jdr 1 S dr I 1 S dr IR12
2
1
2
j
d
r
E
d
r
E
dr
j E E
x
2
2
2
2
12
Edr
1
R12
2
1
2
2
E
dr 12
1
IR12 1 2 12
– закон Ома для неоднородного участка цепи
(интегральная форма)

8.

Постоянный электрический ток
Закон Ома для неоднородного участка цепи
ЭДС (электродвижущая сила)
2
12
E dr
1
ЭДС – величина, численно равная работе по перемещению
единичного положительного заряда по данному пути
Измерение ЭДС
Идеальный вольтметр
r
1
2
Реальный вольтметр
1
2
I
V
V
RV
0 1 2
V =
r
V
RV
RV r
RV r
V RV I

9.

Постоянный электрический ток
Закон Ома для замкнутой цепи
r
IR12 1 2 12
1 2
IR12 12
R
I ( R r)
– закон Ома для замкнутой цепи

10.

Постоянный электрический ток
Разветвленные цепи. Правила Кирхгофа
1 правило Кирхгофа
Ik
В соответствии с законом сохранения заряда
в случае постоянных токов:
алгебраическая сумма токов, сходящихся в
узле, равна нулю
I
k
0
Правило знаков:
(+) – токи, идущие к узлу
(–) – токи, исходящие из узла
(или наоборот)

11.

Постоянный электрический ток
Разветвленные цепи. Правила Кирхгофа
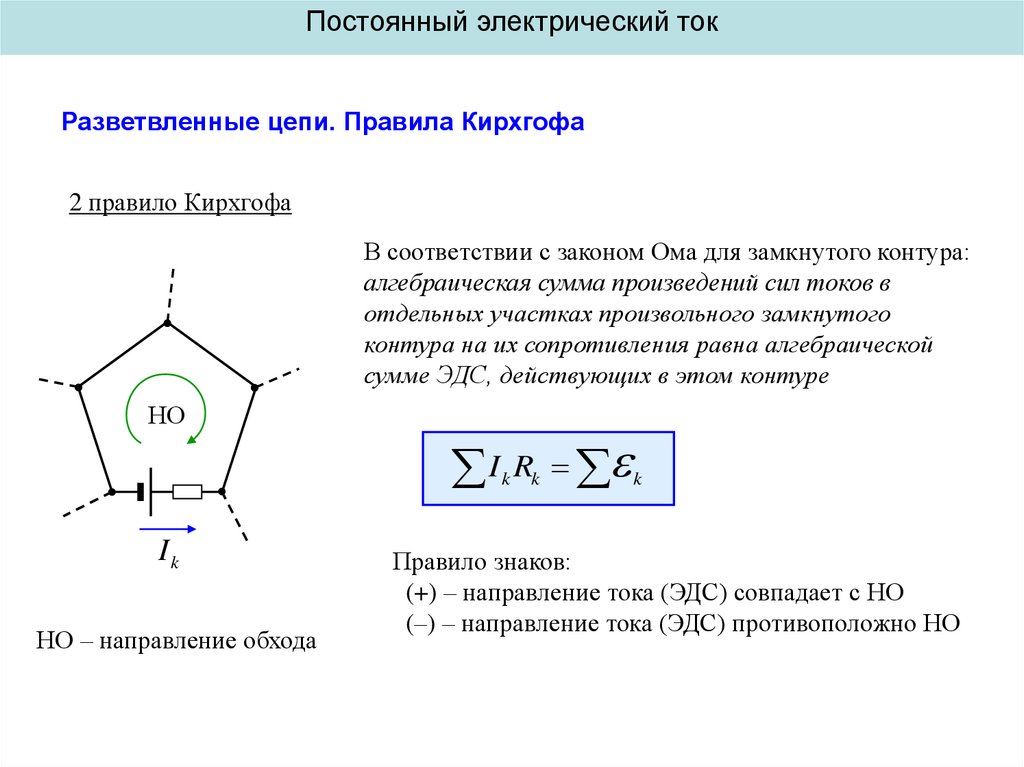
2 правило Кирхгофа
В соответствии с законом Ома для замкнутого контура:
алгебраическая сумма произведений сил токов в
отдельных участках произвольного замкнутого
контура на их сопротивления равна алгебраической
сумме ЭДС, действующих в этом контуре
НО
I R
k
Ik
НО – направление обхода
k
k
Правило знаков:
(+) – направление тока (ЭДС) совпадает с НО
(–) – направление тока (ЭДС) противоположно НО

12.

Постоянный электрический ток
Разветвленные цепи. Правила Кирхгофа
Метод узловых потенциалов
Ik
В основе метода лежат уравнения 1 правила Кирхгофа.
Неизвестными являются значения узловых потенциалов i .
Значение одного узлового потенциала условно принимается
равным нулю 0=0.
1 2
R 0
k
Ik
где N – число узлов.
i 0,
,N 2,

13.

Постоянный электрический ток
Разветвленные цепи. Правила Кирхгофа
Метод контурных токов
in
В основе метода лежат уравнения 2 правила Кирхгофа.
Неизвестными являются фиктивные контурные токи in.
Значение тока в ветви находится алгебраическим сложением
всех проходящих через нее контурных токов.
Проще рассматривать простые контуры.
i
n k
Ik
Rk k
Ik
где N – число контуров.
i 1,
,N ,

14.

Постоянный электрический ток
Разветвленные цепи. Правила Кирхгофа
Метод правил Кирхгофа
1
R1
i1
2
R2
1
I2
I1
I1 I 2 I 3 0
I1R1 I 2 R2 1 2
I R I R
2
3
2 2 3 3
0
i2
3
R3
I3
Метод узловых потенциалов
1 0 1 1 0 2 1 0 3
0
R1
R2
R3
Метод контурных токов
i1R1 (i1 i2 ) R2 1 2
(i2 i1 ) R2 i2 R3 2 3

15.

Постоянный электрический ток
Закон Джоуля-Ленца
Однородный участок цепи
R
1
Работа сил электрического поля по перемещению заряда dQ
2
2
2
1
1
dA dQEdr dQ Edr dQU
dQ Idt
dA
U2
2
P
UI I R
dt
R
P RI 2
– тепловая мощность тока
– закон Джоуля-Ленца
(интегральная форма)

16.

Постоянный электрический ток
Закон Джоуля-Ленца
Однородный участок цепи
E
j u
dV
dF ( dV ) E
Мощность, развиваемая силами электрического поля:
dP dFu ( dV ) Eu ( jE )dV
Объемная плотность мощности:
dP dV jE
– закон Джоуля-Ленца
(локальная форма)

17.

Постоянный электрический ток
Закон Джоуля-Ленца
Неоднородный участок цепи
1
Работа сторонних сил и сил электрического поля
по перемещению заряда dQ
R
2
dA dQ( E E )dr dQ(U )
2
1
dQ Idt
dA
P
UI I
dt
Для замкнутой цепи:
P I

18.

Постоянный электрический ток
Закон Джоуля-Ленца
Неоднородный участок цепи
E E
j u
dF ( dV )( E E )
Мощность, развиваемая силами электрического поля:
dP dFu ( dV )( E E )u j ( E E )dV
dV
Объемная плотность мощности:
dP dV j ( E E )
– закон Джоуля-Ленца
(локальная форма)

19.

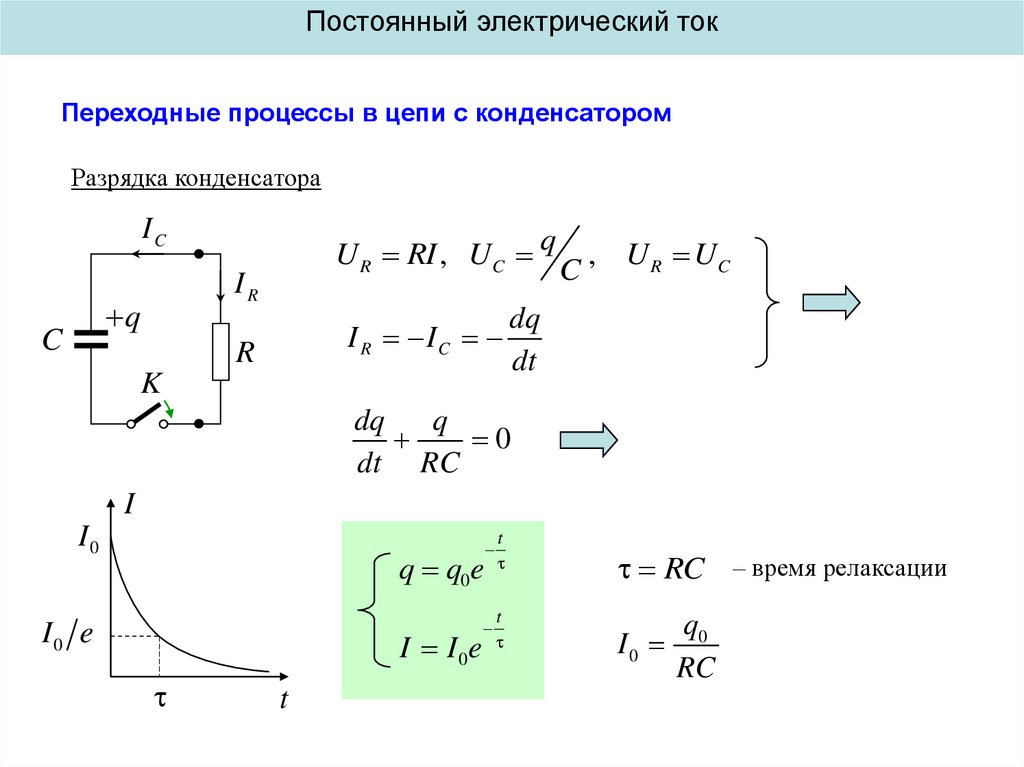
Постоянный электрический ток
Переходные процессы в цепи с конденсатором
Разрядка конденсатора
IC
IR
q
C
U R RI , UC q
C
, U R UC
dq
I R IC
dt
R
K
dq
q
0
dt RC
I
I0
t
t
q q0e
I0 e
I I 0e
t
RC – время релаксации
I0
q0
RC

20.

Постоянный электрический ток
Переходные процессы в цепи с конденсатором
Зарядка конденсатора
I
IR 1 2
2 K
q
R
IC
C
,
q
2 1
C
dq
I IC
dt
dq C q
dt
RC
1
I
I0
t
q qm (1 e )
I0 e
I I 0e
t
t
RC – время релаксации
qm C , I 0
R

21.

Постоянный электрический ток
Классическая электронная теория металлов
l – длина свободного пробега
+
+
e
– время свободного пробега
v – средняя тепловая скорость электронов
l
v
Основные положения теории:
1. Электроны проводимости взаимодействуют только с ионами решетки
посредством столкновений.
2. Движение электронов подчиняется законам Ньютона.
3. При неупругом соударении с ионом электрон передает всю избыточную
кинетическую энергию решетке.

22.

Постоянный электрический ток
Классическая электронная теория металлов
Закон Ома
Среднее смещение электронов за время равно
a 2
eE 2
s
2
2me
Отсюда скорость дрейфа электронов
u
s
eEl
2mev
Если n – концентрация электронов проводимости
e2nl
j neu
E
2mev
j E ,
e2nl
2mev

23.

Постоянный электрический ток
Классическая электронная теория металлов
Закон Джоуля-Ленца
При столкновении электрон теряет в среднем энергию
eEl
meu 2
, где u a
me v
2
С учетом частоты столкновений электрона
dP
e2nl 2
n
E
dV
2mev
dP
E 2 ,
dV
e2nl
2mev
v
l

24.

Постоянный электрический ток
Закон Видемана-Франца
Высокая электро- и теплопроводность металлов обусловлена электронами
проводимости. Роль ионов решетки незначительна.
aT
– коэффициент теплопроводности,
– удельная электропроводность,
a – постоянная.
- закон Видемана-Франца
Молекулярно-кинетическая теория:
1
3
nvcV l , где
cV – изохорная теплоемкость, приходящаяся на один электрон проводимости
2 mv 2 cV
3 e2
cV 3 2 k
mv 2 ~ 3kT
2
k
3 T
e