Электрический ток

1. Лекция № 4s (тема для самостоятельной проработки студентами)

ЭЛЕКТРИЧЕСКИЙ ТОК
Литература: Иродов И.Е. Электромагнетизм.
Основные законы. — М. — С.-П.: Физматлит, 2000.

2. Носители тока в средах

Электрический ток перенос заряда q
через поверхность S (через сечение
проводника).
Ток может течь в твердых телах
(металлы и полупроводники), в жидкостях
(электролиты) и в газах (газовый разряд).
Носители тока (свободные заряженные
частицы в проводящей среде) электроны,
ионы, либо макрочастицы, несущие на себе
избыточный заряд.

3.

При включении электрического поля скорость
v u
носителей
v скорость хаотического (теплового)
движения носителей
u скорость упорядоченного движения
(дрейфа) носителей
т.к.
v 0
v u u ,
Электрический ток упорядоченное
движение электрических зарядов.

4. Сила и плотность тока

Сила тока (количественная характеристика
электрического тока)
dq
I
dt
(4s.1)
величина заряда, переносимого через
рассматриваемую поверхность S в единицу
времени. В СИ I = [А].

5.

Постоянный ток не изменяется со временем
Вектор плотности тока j
Его модуль
dI
j
,
d S
q
I
t
(4s.2)
где dI – сила тока через элементарную
площадку
dS,
перпендикулярную
направлению движения носителей.
j u

6.

Если ток создается носителями обоих
знаков, то сила тока
d q d q
I
dt
dt
(4s.3)
Плотность тока:
j e n u e n u u u
(4s.4)
где e+, e – элементарные «+» и «–» заряды;
n+, n – концентрации, ρ+, ρ – объемные
плотности зарядов «+» и «–» носителей.

7.

Скорости дрейфа «+» и «–» носителей
u u
Тогда
j u u
Поле
j
можно изобразить
с помощью линий
тока
E
j
Сила тока через поверхность
I j d S jn d S
S
S
(4s.5)

8. Уравнение непрерывности

В силу закона сохранения заряда, сила
тока через замкнутую поверхность S равна
скорости убывания заряда, содержащегося в
объеме V, ограниченном этой поверхностью.
Уравнение непрерывности:
dq
j d S dt
S
Представим
(4s.6)
q dV ,
V

9.

согласно теореме Остроградского-Гаусса
j d S j dV
S
V
Подставив в (4s.6) , получаем
d
jdV d t dV t dV
V
V
V
Уравнение
непрерывности
дифференциальной форме
j
t
в
(4s.7)

10.

Согласно (4s.7) в точках, для которых
j 0
существуют источники j
(источники
тока) и происходит убывание заряда.
В случае стационарного тока
0
t
const ,
получаем условие стационарности:
j 0
(4s.8)

11.

В этом случае вектор j
не имеет источников, а линии тока нигде не
начинаются и нигде не заканчиваются
(замкнуты сами на себя) и
j
dq/dt = 0
S
jd S 0
S

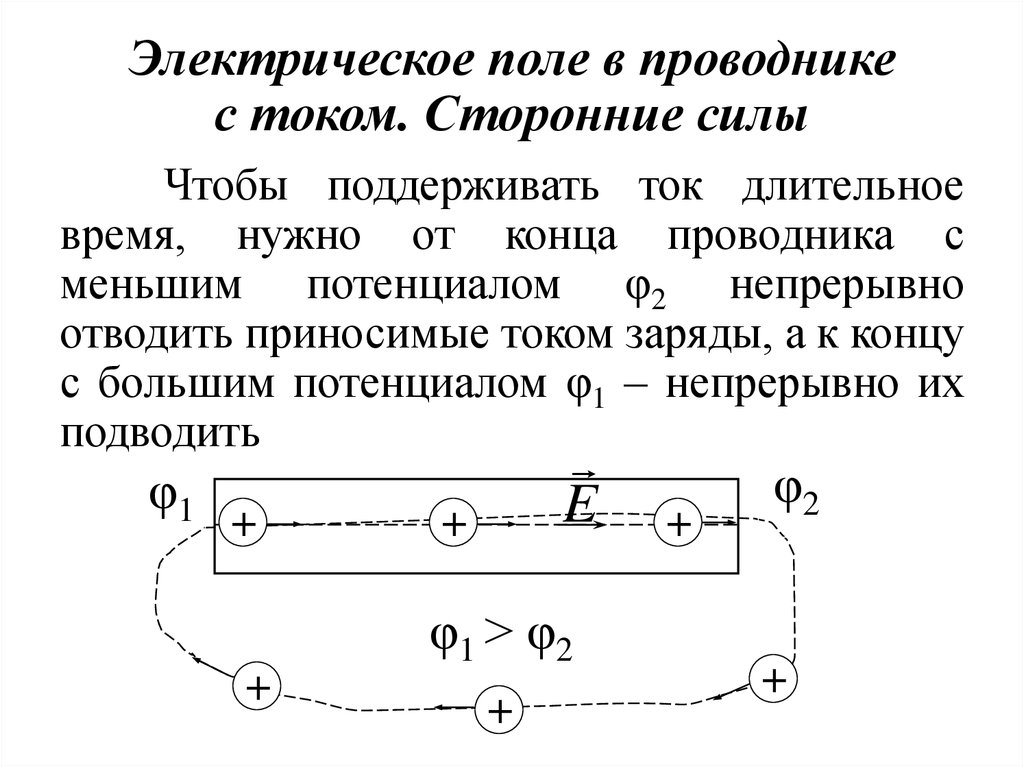
12. Электрическое поле в проводнике с током. Сторонние силы

Чтобы поддерживать ток длительное
время, нужно от конца проводника с
меньшим потенциалом φ2 непрерывно
отводить приносимые током заряды, а к концу
с большим потенциалом φ1 – непрерывно их
подводить
φ1
+
E
+
φ1 > φ2
+
+
+
φ2
+

13.

Перенос «+» зарядов в направлении
возрастания потенциала (против кулоновских
сил э/ст поля) осуществляется сторонними
(неэлектростатическими) силами.
Для поддержания тока постоянным
необходимы сторонние силы, действующие
либо на всей цепи, либо на ее отдельных
участках

14.

Величина, равная работе сторонних сил
над единичным «+» зарядом, называется
электродвижущей
силой
(ЭДС),
действующей в цепи (или на ее участке):
ε A q
(4s.9)
Размерность ЭДС в СИ – [B].
Напряженность поля сторонних сил
* *
(4s.10)
E F q
где
*
F
– сторонняя сила,
q – положительный заряд

15. Работа сторонних сил над зарядом q на участке цепи 1-2

2
*
*
A12 F dl q E dl
2
1
1
ЭДС на участке 1-2
ε12 A12
*
q E dl
2
(4s.11)
1
ЭДС в контуре
*
ε E dl
L
(4s.12)

16.

В электрической цепи, состоящей из
системы проводников и источников
тока
действуют и кулоновское
поле E и поле
сторонних сил E . Результирующее поле
E E E
действует на заряд с силой
F F F q E E
Работа, совершаемая этой силой над зарядом
на участке цепи 1-2
2
*
A12 q E d l q E d l q( 1 2 ) qε12
2
1
1

17.

Величина, численно равная работе,
совершаемой кулоновскими и сторонними
силами
при
перемещении
единичного
положительного
заряда,
называется
падением напряжения (напряжением) на
участке цепи 1-2:
U12 A12 q ( 1 2 ) ε12 (4s.13)
На однородном участке цепи не
действуют сторонние силы. Для него
U12 1 2
На неоднородном участке
действуют сторонние силы. Для него
U12 1 2 ε12
цепи

18. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах

Закон Ома в интегральной форме
• для однородного участка проводника
U
I
R
где
(4s.14)
U 1 2
R – электрическое сопротивление проводника,
в СИ R = [Ом], 1 [Ом] = 1 [B] / 1[A].

19.

• для
однородного
проводника
цилиндрического
l
R
S
ρ – удельное электрическое сопротивление
материала проводника в [Ом м], l – его длина,
S – площадь поперечного сечения проводника
Закон Ома в дифференциальной форме
dl
Рассмотрим
изотропный проводник
E j
E
j
dS
Подставляя в (4s.14)
I j d S;
U E dl;
dl
R
dS

20.

получаем
Ed l
jd S
dS
d l
Плотность тока
1
j E
Дифференциальная форма закона Ома в
векторном виде
1
(4s.15)
j E E
σ = 1/ρ – электропроводность материала
проводника, в СИ σ = [См/м]. 1См
(сименс)=1/Ом

21. Если электрический ток обусловлен носителями одного знака, то

j enu
С учетом (4s.15)
enu E
Носители характеризуются подвижностью
b u E
Дифференциальная форма закона Ома
для неоднородного участка цепи
u~ E E j ~ E E
j E E
(4s.16)

22.

Для случая тонких проводников (или
контура тока в объемном проводнике) и
совпадения направления тока с осью
проводника плотность тока j можно считать
постоянной во всех точках сечения провода S.
Из (4s.16)
2
j dl 2 2 *
E d l E d l 1 2 ε12 (4s.17)
1
1
1
Заменим 1 ; j d l jl d l ;
jl I S
причем I const

23. Тогда

2
1
где
2
jdl
dl
I
1 S
2
dl
S R
1
– полное сопротивление участка цепи между
сечениями 1 и 2
(4s.17) преобразуется к виду
(4s.18)
IR 1 2 ε12
или
1
(4s.19)
I 1 2 ε12
R

24. (4s.18), (4s.19) - интегральные формы з-на Ома для неоднородного участка цепи

ε12 и I – алгебраические величины: ε12>0
способствует движению «+» носителей в
направлении (1-2), ε12<0 – препятствует.
1 2
Закон Ома для замкнутой цепи
I ε R,
R R0 r
(4s.20)
где R – полное сопротивление замкнутой
цепи, r – внутреннее сопротивление
источника ЭДС, R0 – сопротивление внешней
цепи.

25. Закон Джоуля-Ленца в интегральной форме

Работа постоянного тока
A UIt
где It = q – заряд, прошедший за время t через
каждое сечение проводника, U – напряжение,
приложенное к концам проводника
Для однородного участка цепи
A q 1 2
Для неоднородного участка цепи
A q 1 2 q ε12

26. При протекании тока в проводнике выделяется тепло

При протекании
выделяется тепло
тока
в
проводнике
Q UIt
Используя (4s.14), получаем интегральную
форму закона Джоуля-Ленца
2
(4s.21)
Q RI t
В случае переменной во времени силы тока
джоулево тепло
t
Q R I d t
2
0
(4s.22)

27. Закон Джоуля-Ленца в дифференциальной форме

dl
δQ
где
Согласно
(4s.22)
в
выделенном в проводнике
цилиндрическом объеме, за
время
dt
выделяется
j
элементарное тепло
2
dS
RI
dt
Q
d l
2
2
jd S d t j dV d t
dS
dV d S d l

28. Удельная тепловая мощность тока

Q
Qуд
dV d t
Дифференциальная форма закона ДжоуляЛенца
2
Qуд j или Q уд j 2 (4s.23)
– наиболее общая форма записи закона, для
любых проводников вне зависимости от их
формы, однородности и природы сил,
возбуждающих электрический ток.
Для однородного участка проводника
2
Qуд j E E

29. Самостоятельно: Правила Кирхгофа для разветвленных электрических цепей

Узел (цепи) –
точка, в которой
сходятся более двух проводников.
Первое правило Кирхгофа. Алгебраическая
сумма токов, сходящихся в узле, равна нулю
N
Ii 0
I2
I1
i 1
I3
I1 I 2 I 3 0
(4s.24)
– следствие условия
стационарности,
подтверждается
законом
сохранения
электрического заряда.

30. Второе правило Кирхгофа: алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопроти

Второе правило Кирхгофа: алгебраическая
сумма произведений сил токов в отдельных
участках произвольного замкнутого контура
на их сопротивления равна алгебраической
сумме ЭДС, действующих в этом контуре:
I2
R2
ε2
φ3 I1 R1
φ1
I3
N
N
I i Ri εi
i 1
R3
ε3
ε1 φ2
(4s.25)
i 1
– следует из з-на Ома для
неоднородного участка цепи,
относится к вы-деленному в
разветвленной
цепи
замкнутому контуру