Similar presentations:
Электростатика. Постоянный электрический ток
1.
ЛЕКЦИЯ №4.ЭЛЕКТРОСТАТИКА.
ПОСТОЯННЫЙ
ЭЛЕКТРИЧЕСКИЙ ТОК
1
2.
ЭЛЕКТРОСТАТИКА2
Элементарный заряд: е- =1,6·10-19 Кл,
е+=1,6·10-19 Кл .
q n e n e
q>0, если n+>nq<0, если n+<nq=0, если n+=n-
3.
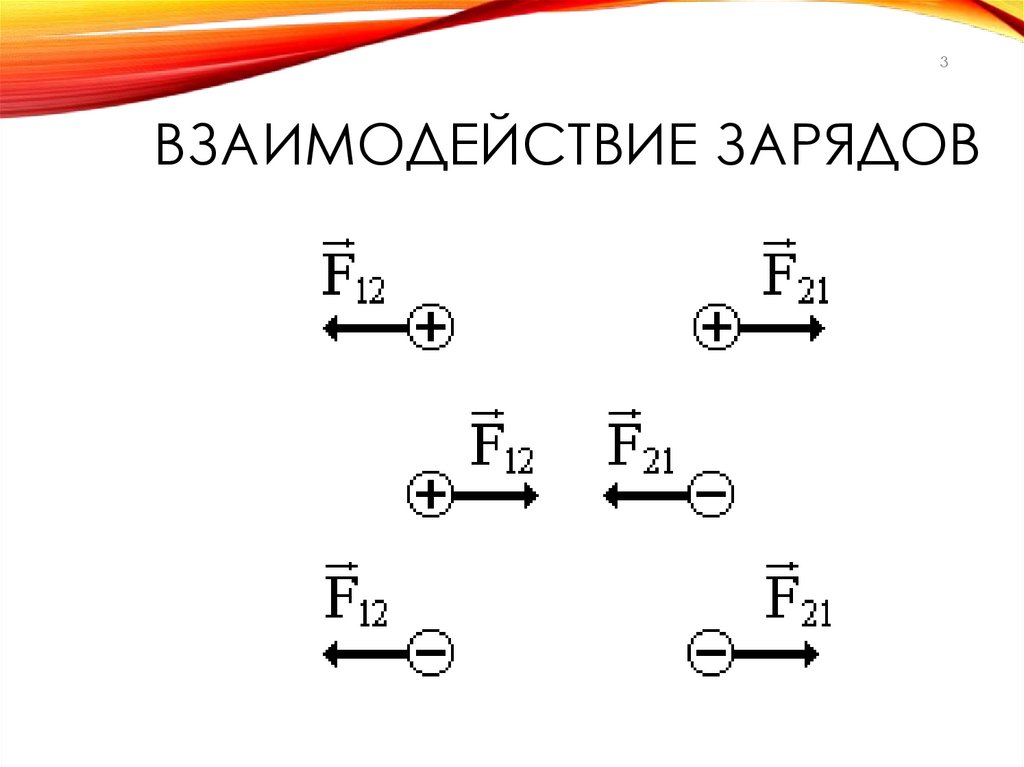
3ВЗАИМОДЕЙСТВИЕ ЗАРЯДОВ
4.
ЗАКОН ВЗАИМОДЕЙСТВИЯТОЧЕЧНЫХ ЗАРЯДОВ
(ЗАКОН КУЛОНА)
4
q1 q 2
F к
r
12
3
r12
q1q2 r12
F к 2
r12 r12
к
1
4 0
9 10
9
в законе Кулона
Н м2
Кл 2
коэффициент пропорциональности
5.
5ЗАКОН КУЛОНА В СКАЛЯРНОЙ ФОРМЕ
q1q2
F к
2
r12
6.
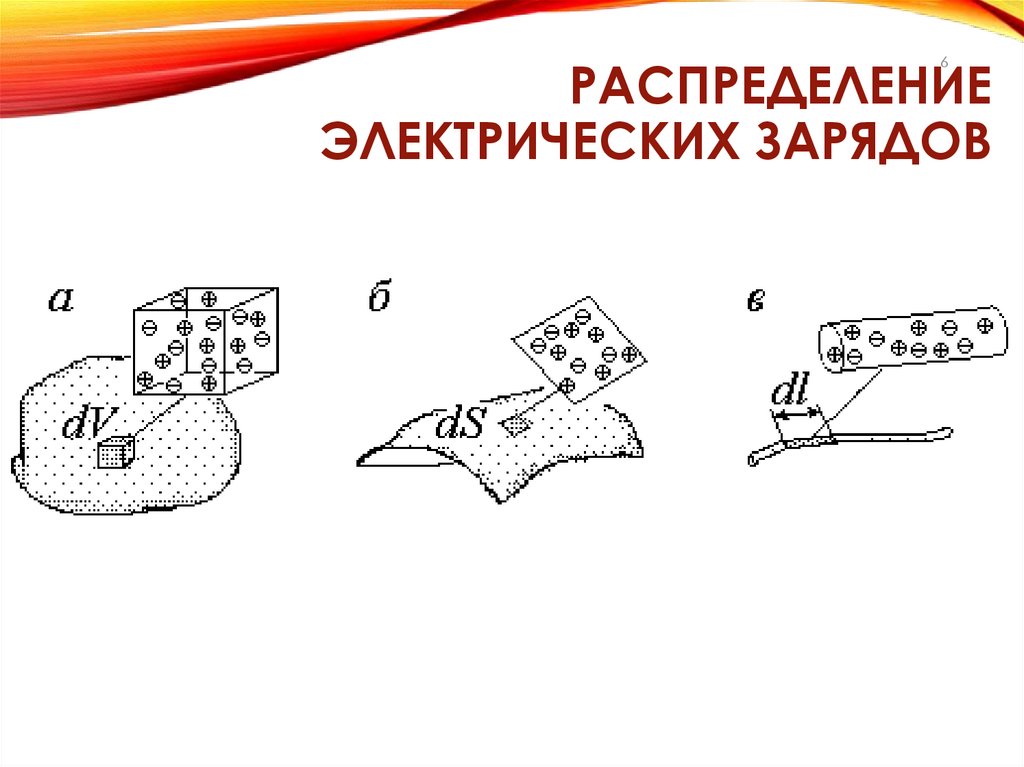
РАСПРЕДЕЛЕНИЕЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
6
7.
7а) Объемная плотность заряда:
q
dq
lim
V 0 V
dV
8.
8Средняя объемная плотность заряда:
q
ср
V
Кл
3
м
9.
9б) Поверхностная плотность заряда:
q dq
lim
S 0 S
dS
q
ср
S
10.
10в) линейная плотность заряда
q dq
lim
l 0 l
dl
q
ср
l
11.
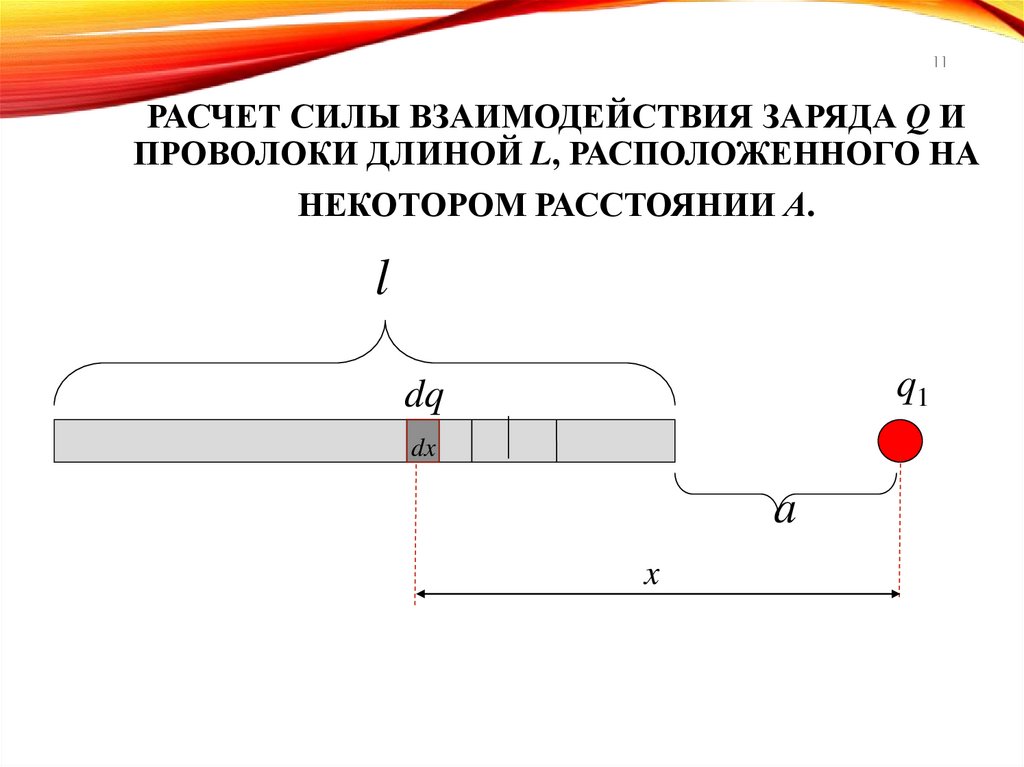
11РАСЧЕТ СИЛЫ ВЗАИМОДЕЙСТВИЯ ЗАРЯДА Q И
ПРОВОЛОКИ ДЛИНОЙ L, РАСПОЛОЖЕННОГО НА
НЕКОТОРОМ РАССТОЯНИИ А.
l
q1
dq
dx
a
x
12.
12Результирующая сила взаимодействия
заряда q и проволоки :
F Fi
n
i 1
13.
По закону Кулона:q1 dq
dF k 2 ,
x
13
14.
14ЛИНЕЙНАЯ ПЛОТНОСТЬ
ЭЛЕКТРИЧЕСКОГО ЗАРЯДА:
dq
dx
dq dx
15.
15a l
a l
q1 dx
F dF k
2
x
a
a
1
1
F k q1
a l a
16.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ16
• Силовая характеристика электрического поля:
q q r
q 1 r
F к 2 к 2 Е
r r
r r
q
F к 2 Е
r
/
17.
НАПРЯЖЕННОСТЬЭЛЕКТРИЧЕСКОГО ПОЛЯ
17
F
E
Q0
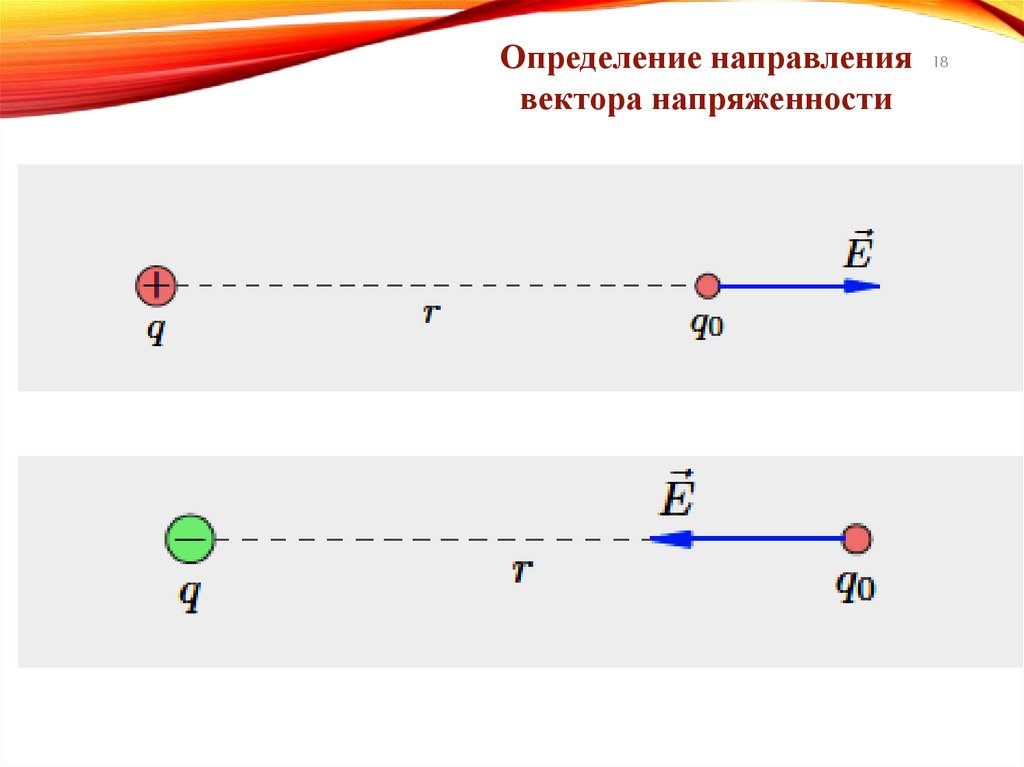
18.
Определение направления 18вектора напряженности
19.
НАПРЯЖЕННОСТЬТОЧЕЧНОГО ЗАРЯДА:
19
Q
r
E
2
4 0 r r
[1В/м]= [1Кл]/ [1м2].
20.
НАПРЯЖЕННОСТЬТОЧЕЧНОГО ЗАРЯДА
В СКАЛЯРНОЙ ФОРМЕ
E
Q
4 0 r
2
20
21.
ГРАФИЧЕСКОЕ ОБОЗНАЧЕНИЕНАПРЯЖЕННОСТИ
21
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ:
Источник
электростатического поля
+
Сток
электростатического
поля
-
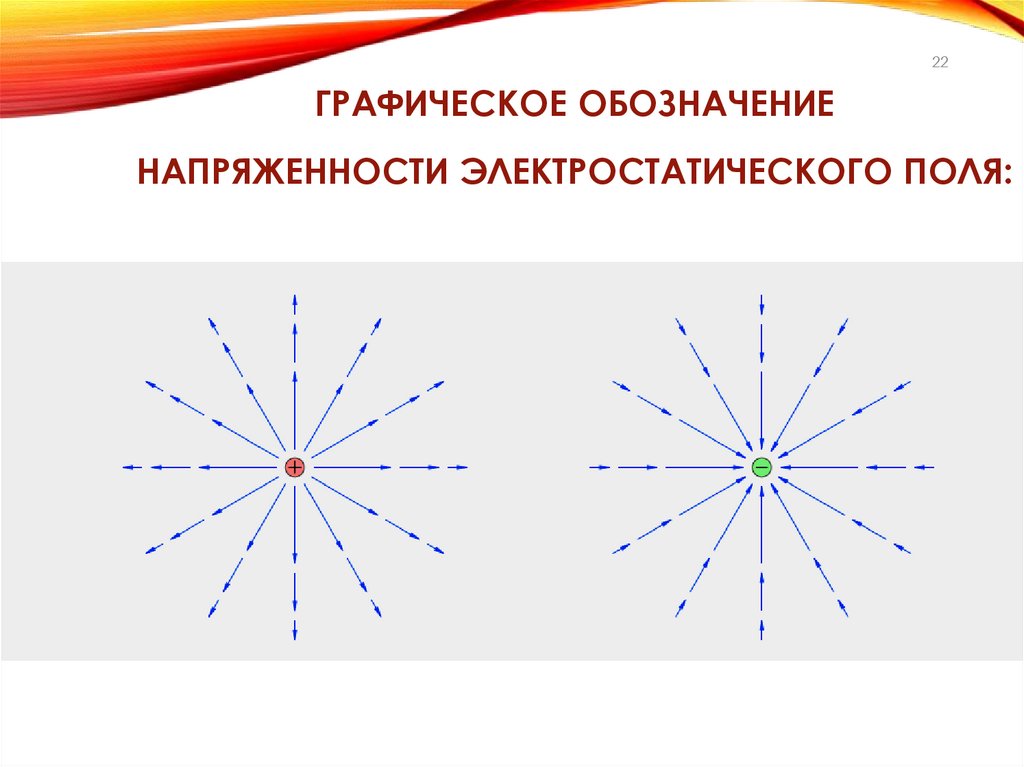
22.
22ГРАФИЧЕСКОЕ ОБОЗНАЧЕНИЕ
НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ:
23.
Принцип суперпозицииэлектростатических полей:
23
E Ei
n
i 1
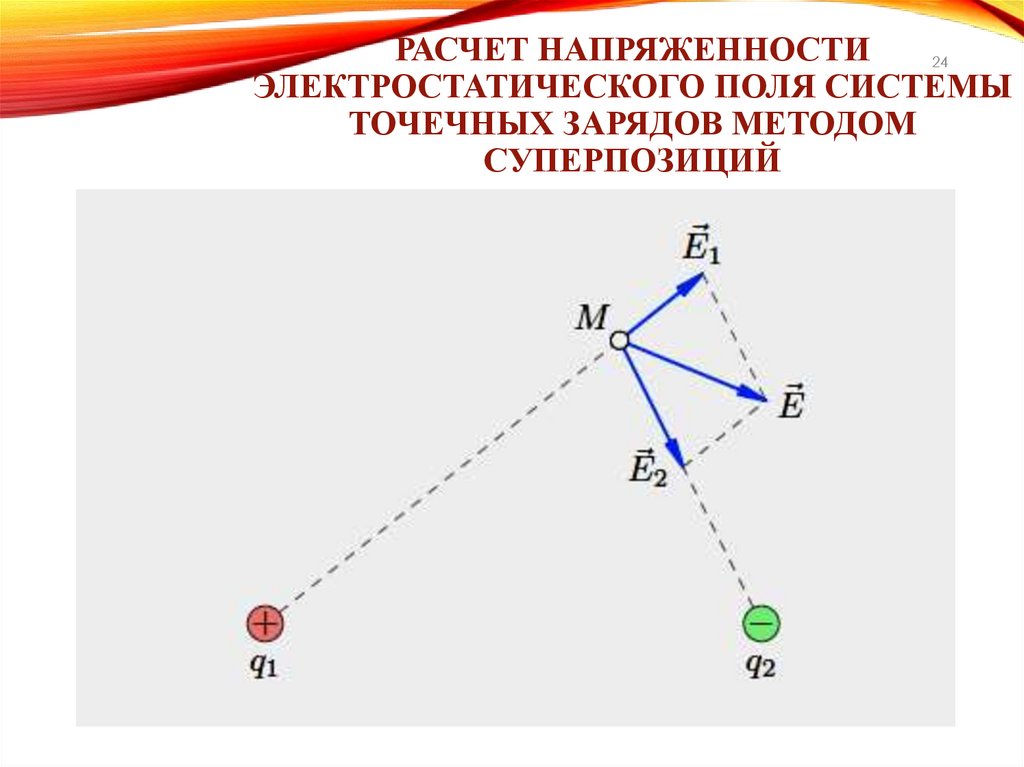
24.
РАСЧЕТ НАПРЯЖЕННОСТИ24
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ СИСТЕМЫ
ТОЧЕЧНЫХ ЗАРЯДОВ МЕТОДОМ
СУПЕРПОЗИЦИЙ
25.
E E1 E 225
E E1 E2 2E1 E2 cos
2
E1
2
q1
4 0 r1
2
E2
q2
4 0 r2
2
26.
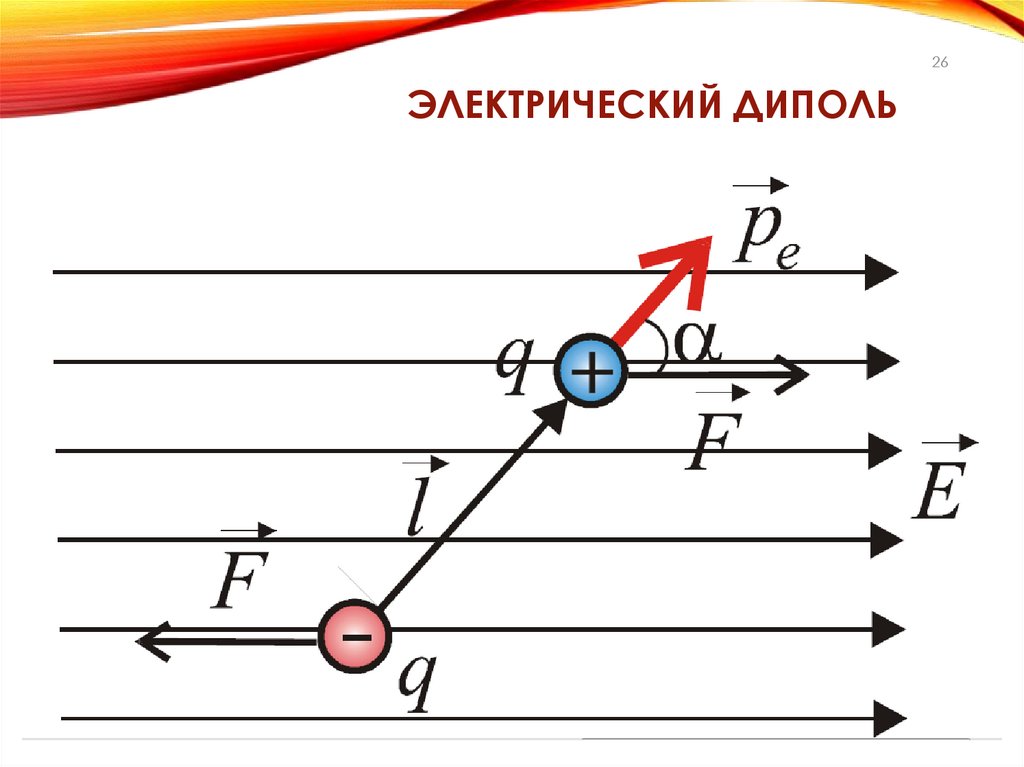
26ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ
27.
27ДИПОЛЬНЫЙ МОМЕНТ
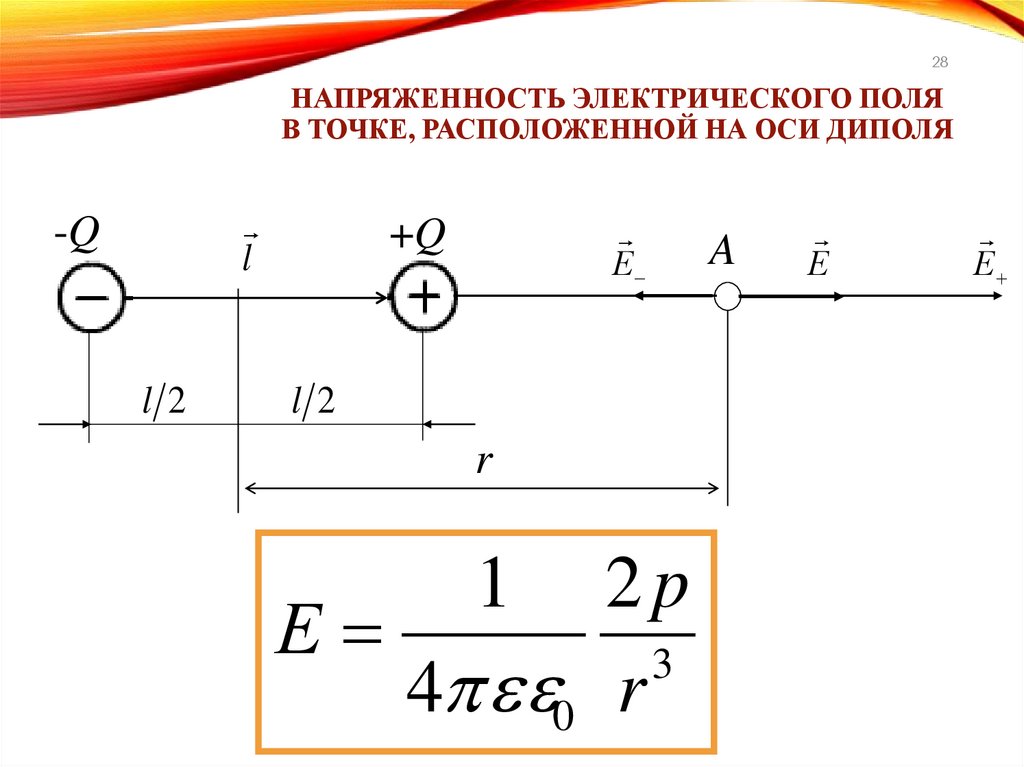
28.
28НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
В ТОЧКЕ, РАСПОЛОЖЕННОЙ НА ОСИ ДИПОЛЯ
l
-Q
l 2
Е
+Q
l 2
r
1
2p
Е
3
4 0 r
A
Е
Е
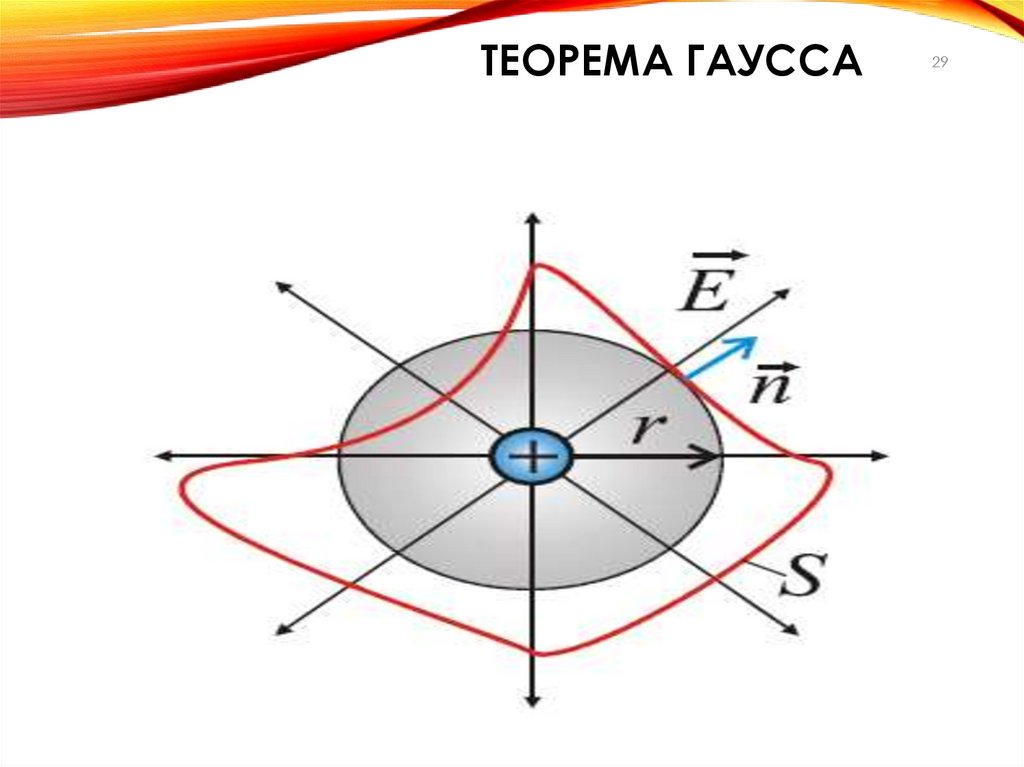
29.
ТЕОРЕМА ГАУССА29
30.
30ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ СКВОЗЬ
СФЕРИЧЕСКУЮ ПОВЕРХНОСТЬ РАДИУСА R,
ОХВАТЫВАЮЩУЮ ТОЧЕЧНЫЙ ЗАРЯД Q,
НАХОДЯЩЕЙСЯ В ЕЕ ЦЕНТРЕ:
ФE E dS E dS cos E , n E dS
S
S
S
31.
31Силовые линии заряда центрально симметричны,
поэтому в каждой точке поверхности этой сферы
проекция вектора Е на внешнюю нормаль (п) имеет
одно и то же значение:
E
q
4 0 r
2
E n cos cos 0 1
32.
ФЕq
4
r
0
S
q
4 0 r
dS
2
4
r
2
2
q
0
32
33.
33ТЕОРЕМА ГАУССА:
Поток вектора напряженности электрического поля в
вакууме сквозь замкнутую поверхность произвольной формы
равен отношению алгебраической суммы зарядов, находящейся
внутри этой поверхности, к электрической постоянной.
34.
34ЕСЛИ
ЭЛЕКТРИЧЕСКИЕ
ЗАРЯДЫ
РАСПРЕДЕЛЕНЫ
НЕРАВНОМЕРНО С ОБЪЕМНОЙ ПЛОТНОСТЬЮ Ρ ЗАРЯДОВ,
РАЗЛИЧНОЙ В РАЗНЫХ МЕСТАХ ПРОСТРАНСТВА, ТО
ТЕОРЕМА ГАУССА ПРИНИМАЕТ ВИД:
35.
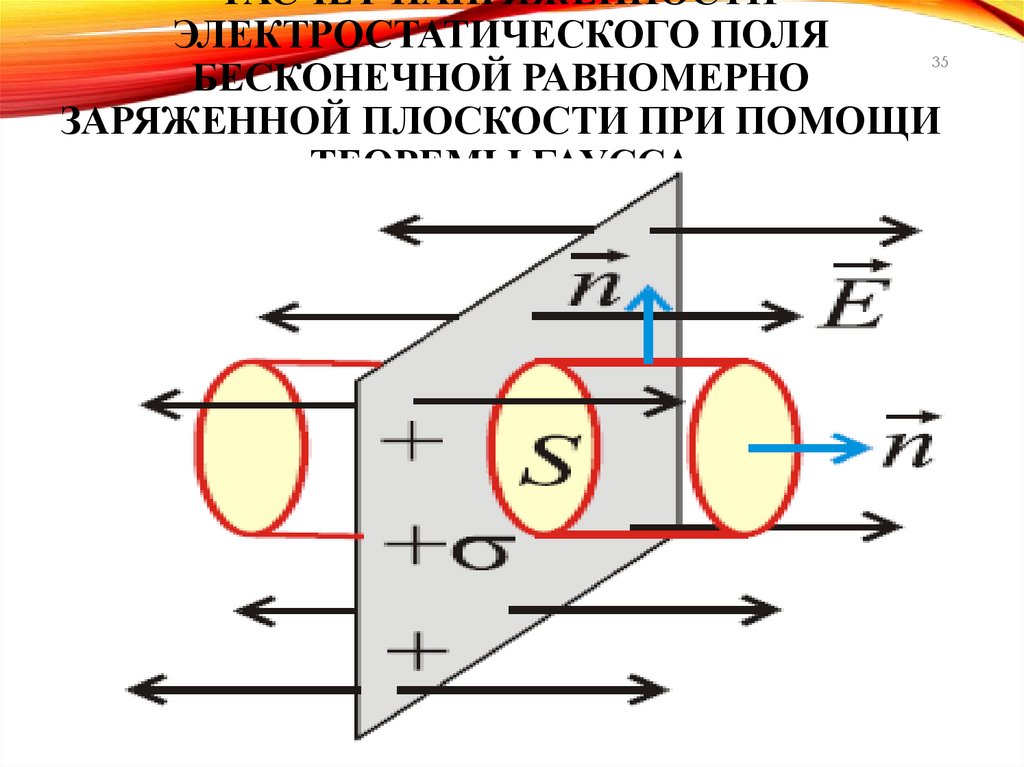
РАСЧЕТ НАПРЯЖЕННОСТИЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
БЕСКОНЕЧНОЙ РАВНОМЕРНО
ЗАРЯЖЕННОЙ ПЛОСКОСТИ ПРИ ПОМОЩИ
ТЕОРЕМЫ ГАУССА
35
.
36.
36• Представим
себе
равномерно
заряженную
бесконечную
плоскость
с
постоянной
поверхностной плотностью заряда σ (рис.).
• Построим бесконечно узкий прямой цилиндр,
пересекающий данную плоскость,
основания
которого параллельны заряженной плоскости и
лежат по разные стороны от нее на одинаковых
расстояниях.
37.
Поток смещения сквозь замкнутую цилиндрическуюповерхность :
37
ФЕ Фбок 2Фосн
Так
как
образующие
цилиндра
параллельны
линиям
напряженности,
то поток вектора напряженности
через
боковую
поверхность цилиндра равен нулю, а полный поток
сквозь цилиндр равен сумме потоков сквозь его основания:
ФЕ 2Фосн 2 E S
38.
38По теореме Гаусса:
ФE
q
0
39.
39q
0
2E S
q S E
2 0
40.
НАПРЯЖЕННОСТЬЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
БЕСКОНЕЧНОЙ РАВНОМЕРНО
ЗАРЯЖЕННОЙ ПЛОСКОСТИ:
40
E
2 0
41.
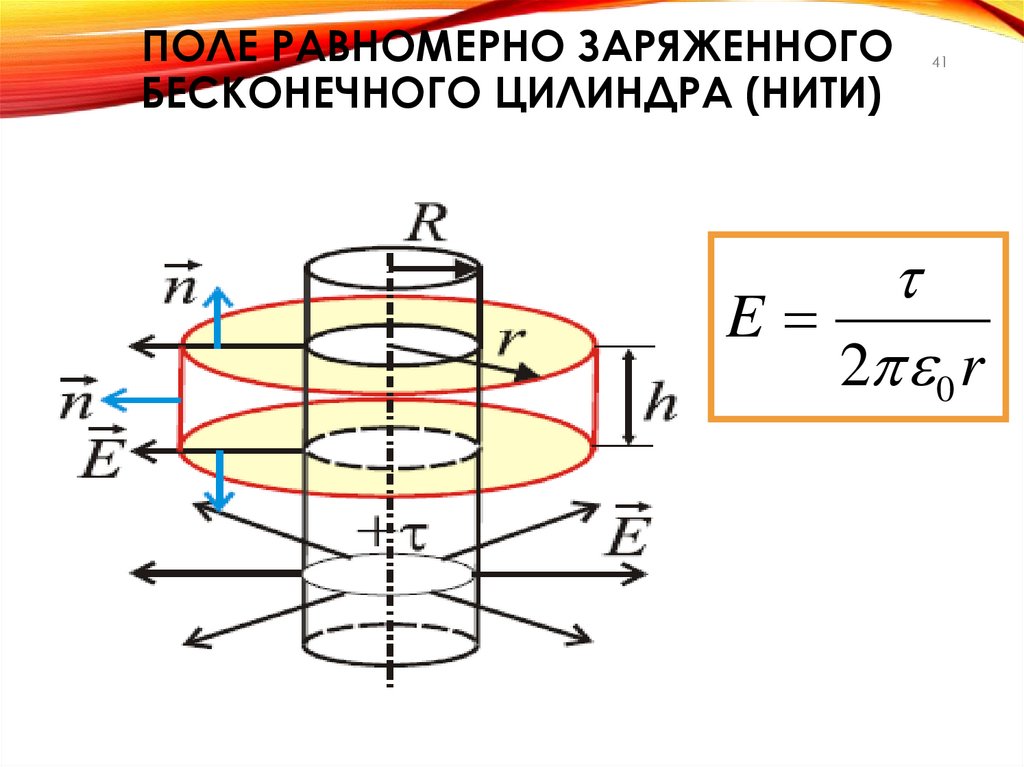
ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГОБЕСКОНЕЧНОГО ЦИЛИНДРА (НИТИ)
41
E
2 0 r
42.
18.12.2023 г.Конденсаторы.
Электрическое поле в
веществе
43.
КОНДЕНСАТОРЫ.ЕМКОСТЬ ПЛОСКОГО
КОНДЕНСАТОРА
44.
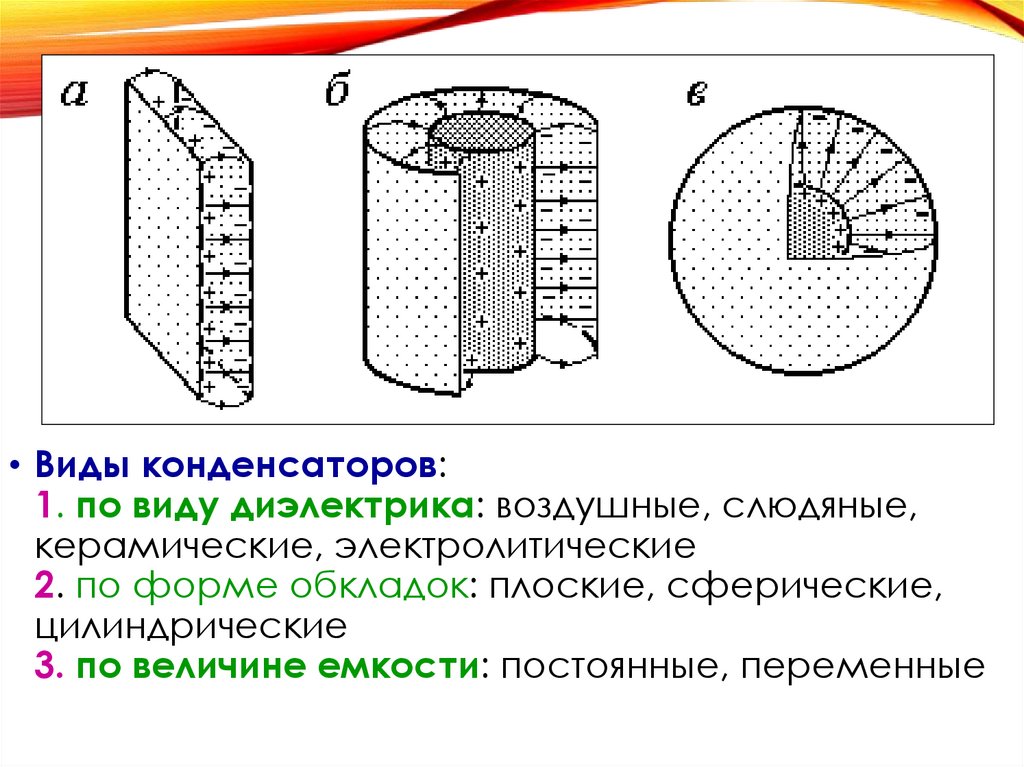
• Виды конденсаторов:1. по виду диэлектрика: воздушные, слюдяные,
керамические, электролитические
2. по форме обкладок: плоские, сферические,
цилиндрические
3. по величине емкости: постоянные, переменные
45.
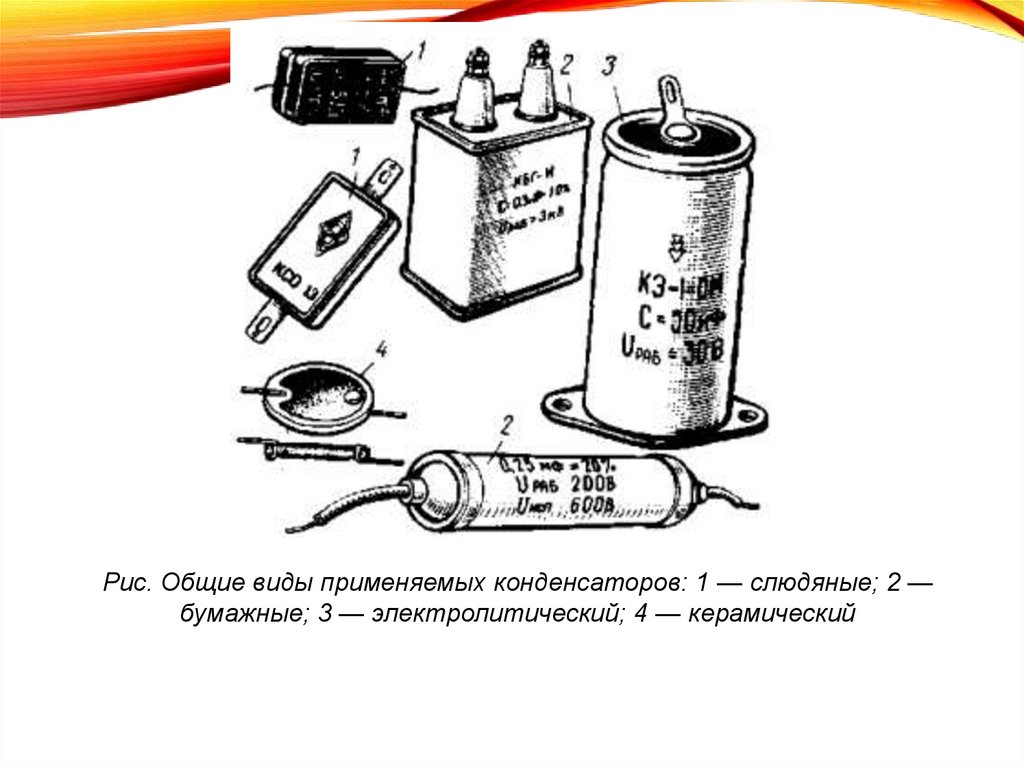
Рис. Общие виды применяемых конденсаторов: 1 — слюдяные; 2 —бумажные; 3 — электролитический; 4 — керамический
46.
Конденсатор переменной емкостиКонденсатор постоянной емкости
47.
ЭЛЕКТРОЕМКОСТЬq
q
C
1 2 U
1Ф= 1
Кулон
Кл
1
Вольт
В
48.
ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГОКОНДЕНСАТОРА
С
0 S
d
49.
ЭЛЕКТРОЕМКОСТЬ СФЕРИЧЕСКОГОКОНДЕНСАТОРА:
4 0 rR
C
R r
50.
ЭЛЕКТРОЕМКОСТЬЦИЛИНДРИЧЕСКОГО
КОНДЕНСАТОРА:
2 0 L
C
R
ln( )
r
51.
ПОСЛЕДОВАТЕЛЬНОЕ ИПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
КОНДЕНСАТОРОВ
52.
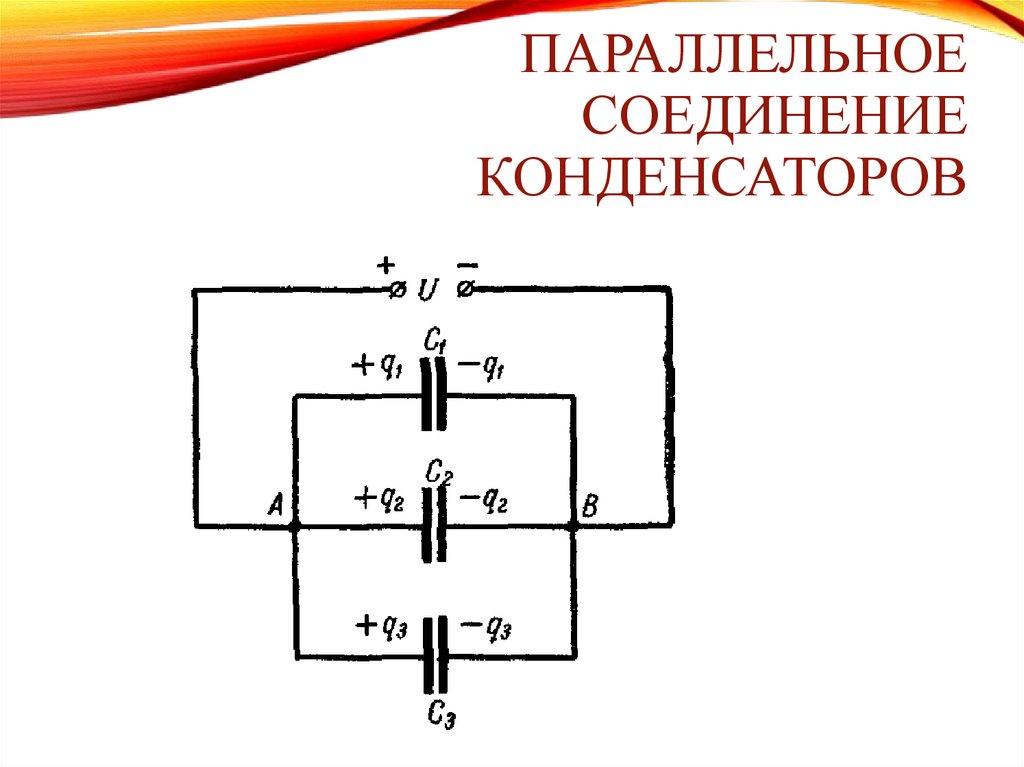
ПАРАЛЛЕЛЬНОЕСОЕДИНЕНИЕ
КОНДЕНСАТОРОВ
53.
U constq1 C1 U , q2 C2 U , ... , qn Cn U
q q1 q2 ... qn
q C1 C2 ... Cn U
q
Cб C1 C2 ... Cn
U
54.
ЭЛЕКТРОЕМКОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНОСОЕДИНЕННЫХ КОНДЕНСАТОРОВ
n
С б Сi
i 1
55.
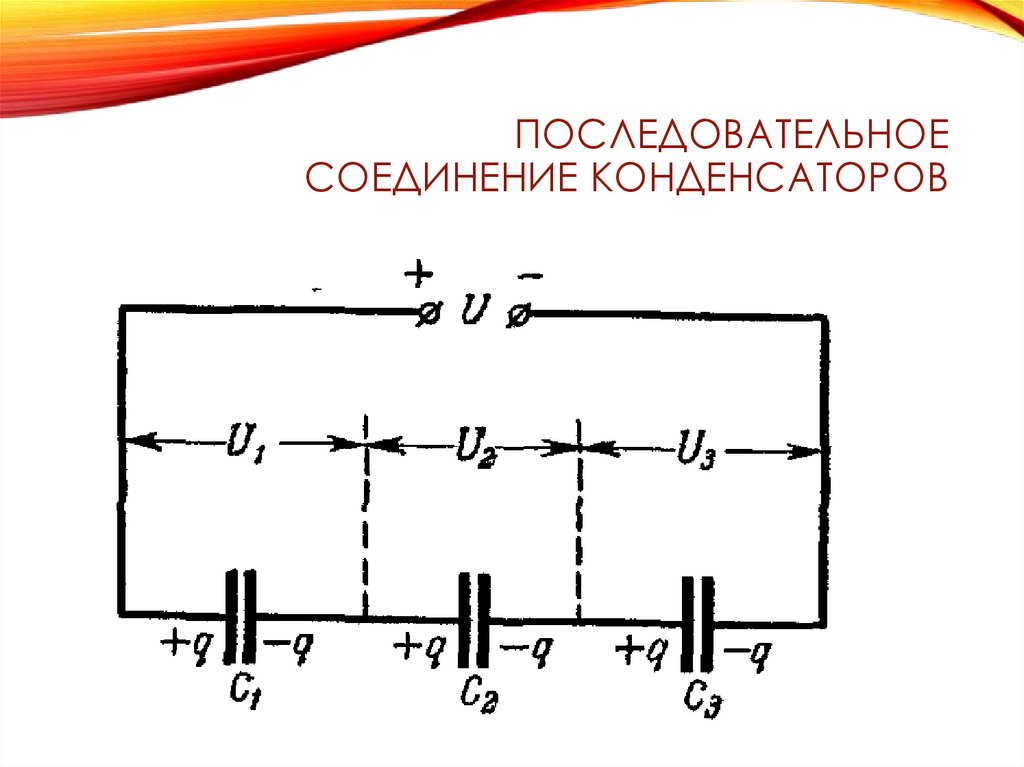
ПОСЛЕДОВАТЕЛЬНОЕСОЕДИНЕНИЕ КОНДЕНСАТОРОВ
56.
nU U i , q const
i 1
q
q
q
U1 , U 2
, ... , U n
C1
C2
Cn
U U1 U 2 ... U n
57.
11
1
U
... q
C
C
C
1
2
n
1 U
1
1
1
...
Cб q C1 C2
Cn
58.
ЭЛЕКТРОЕМКОСТЬ СИСТЕМЫПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ
КОНДЕНСАТОРОВ
n
1
1
Сб i 1 Сi
59.
Сб Ci60.
ЭНЕРГИЯ УЕДИНЕННОГО ПРОВОДНИКАИ КОНДЕНСАТОРА
1
W Q
2
2
q
1
1
2
Wk
qU CU
2C 2
2
61.
ОБЪЕМНАЯ ПЛОТНОСТЬ ЭНЕРГИИЭЛЕКТРИЧЕСКОГО ПОЛЯ
W 0 Е
0
V
2
2
62.
ТИПЫ ДИЭЛЕКТРИКОВ.ПОЛЯРИЗАЦИЯ
ДИЭЛЕКТРИКОВ
63.
ДИЭЛЕКТРИКИ ВЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Полярные
Неполярные
Ионные
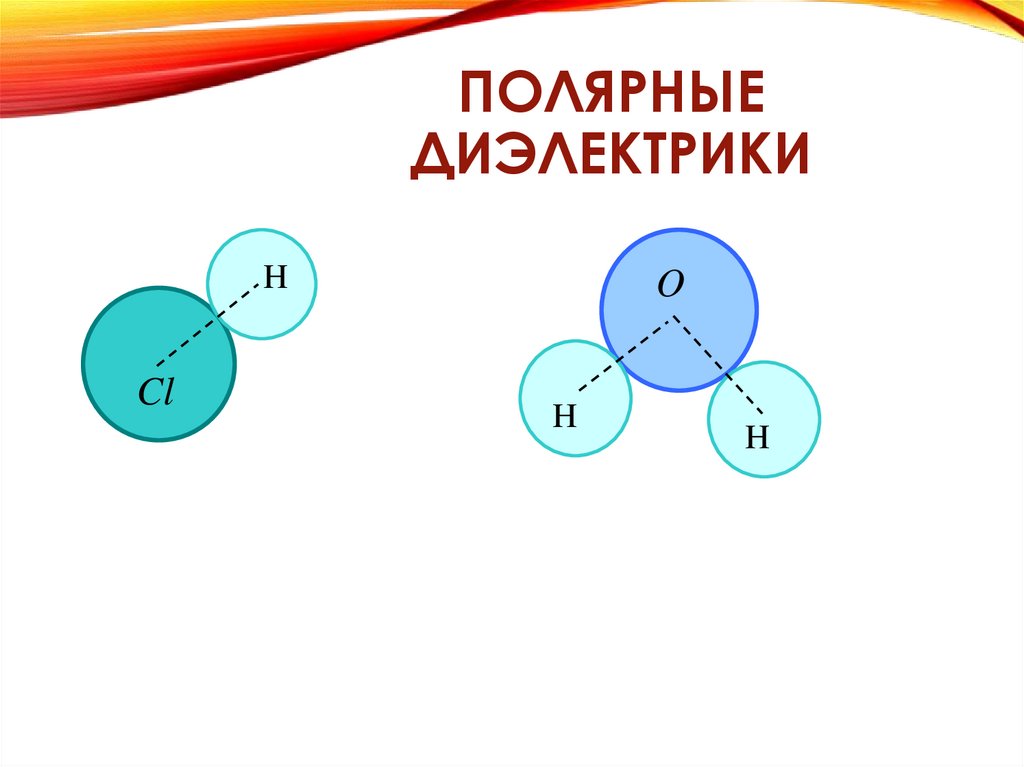
64.
ПОЛЯРНЫЕДИЭЛЕКТРИКИ
H
Cl
O
H
H
65.
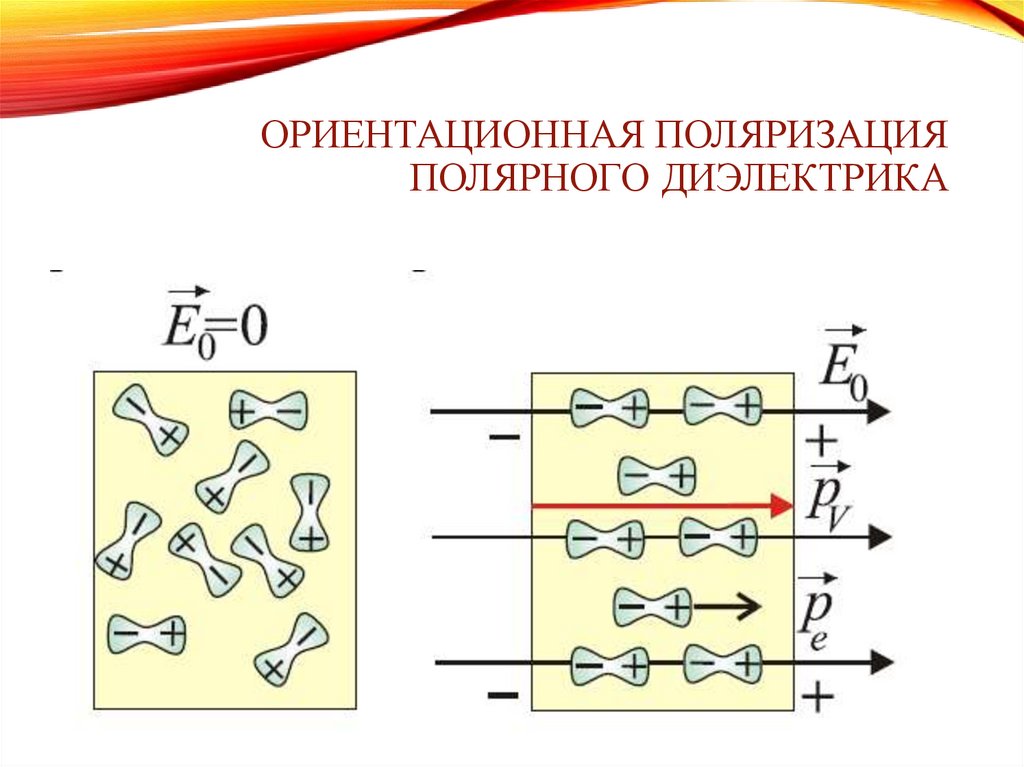
ОРИЕНТАЦИОННАЯ ПОЛЯРИЗАЦИЯПОЛЯРНОГО ДИЭЛЕКТРИКА
66.
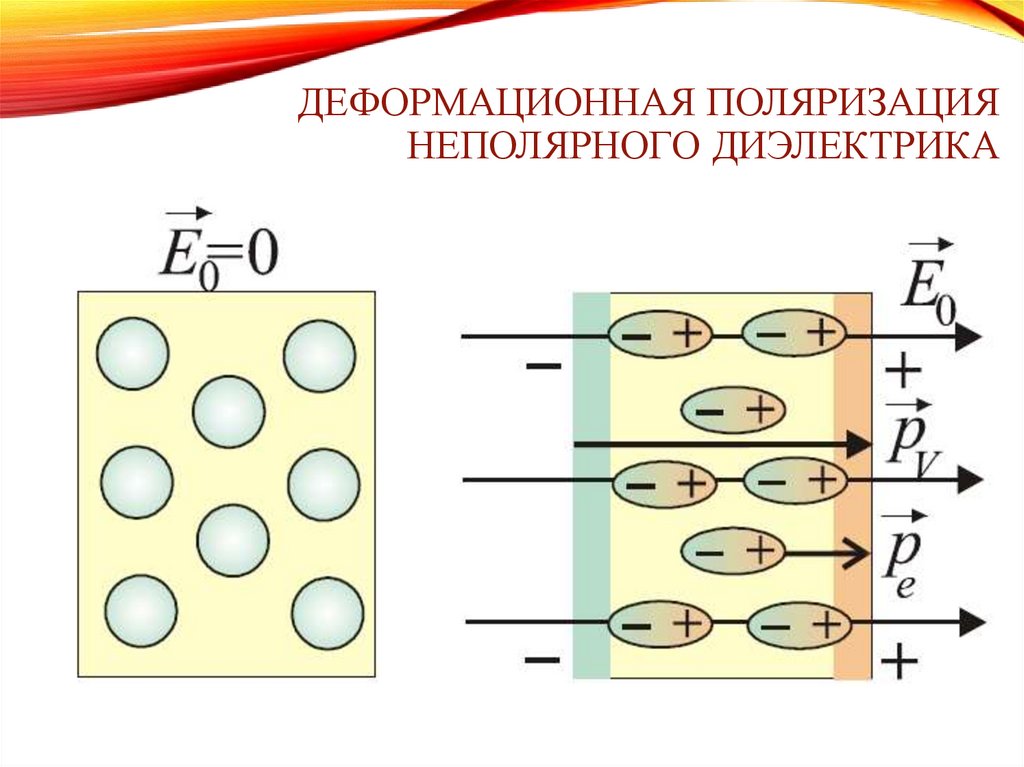
ДЕФОРМАЦИОННАЯ ПОЛЯРИЗАЦИЯНЕПОЛЯРНОГО ДИЭЛЕКТРИКА
67.
67ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА
И ПЛОТНОСТЬ ТОКА.
УСЛОВИЕ СУЩЕСТВОВАНИЯ
ТОКА В ЦЕПИ. СТОРОННИЕ
СИЛЫ. ЭДС.
68.
68УСЛОВИЯ СУЩЕСТВОВАНИЯ
ТОКА В ЦЕПИ:
наличие свободных носителей тока (свободного
заряда);
наличие электрической силы, вынуждающей их
упорядоченно двигаться.
69.
69ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
ЭЛЕКТРИЧЕСКОГО ТОКА
Сила тока
dq
I
dt
1Кл
1
A
1с
70.
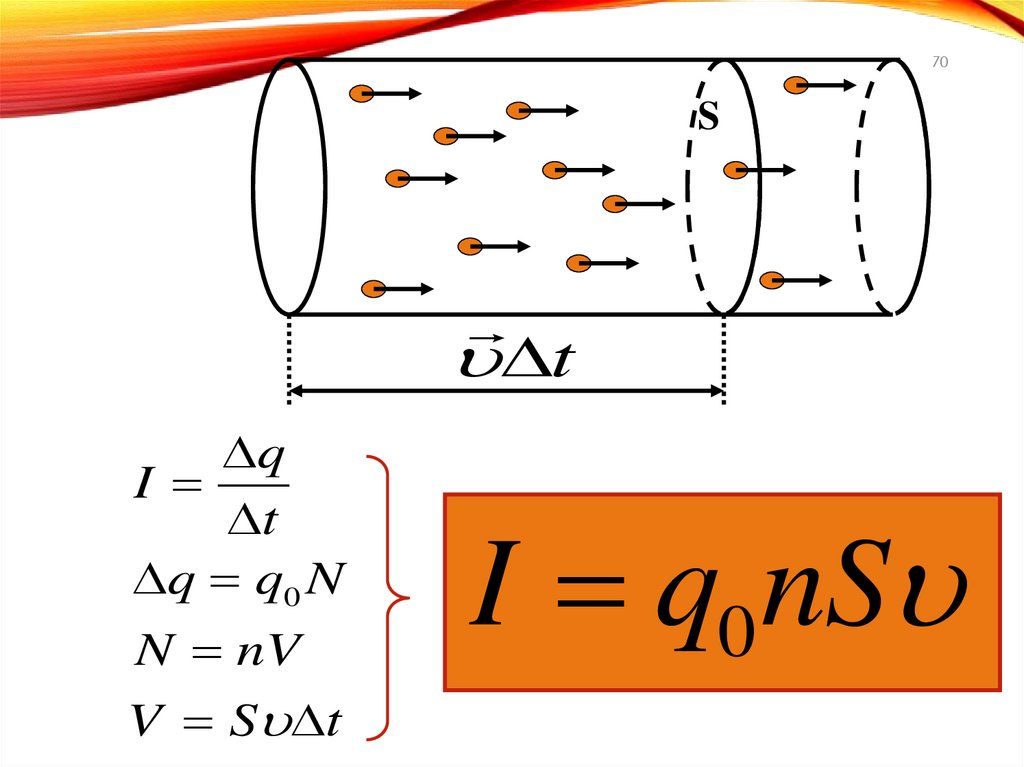
70S
t
q
I
t
q q 0 N
N nV
V S t
I q0 nS
71.
71ПЛОТНОСТЬ ТОКА
dI
j
dS
2
j А/ м
I j dS
S
72.
72ПОСТОЯННЫЙ ТОК
q
I
t
73.
73ЗАКОН ОМА ДЛЯ
ОДНОРОДНОГО УЧАСТКА
ЦЕПИ. СОПРОТИВЛЕНИЕ
ПРОВОДНИКОВ
74.
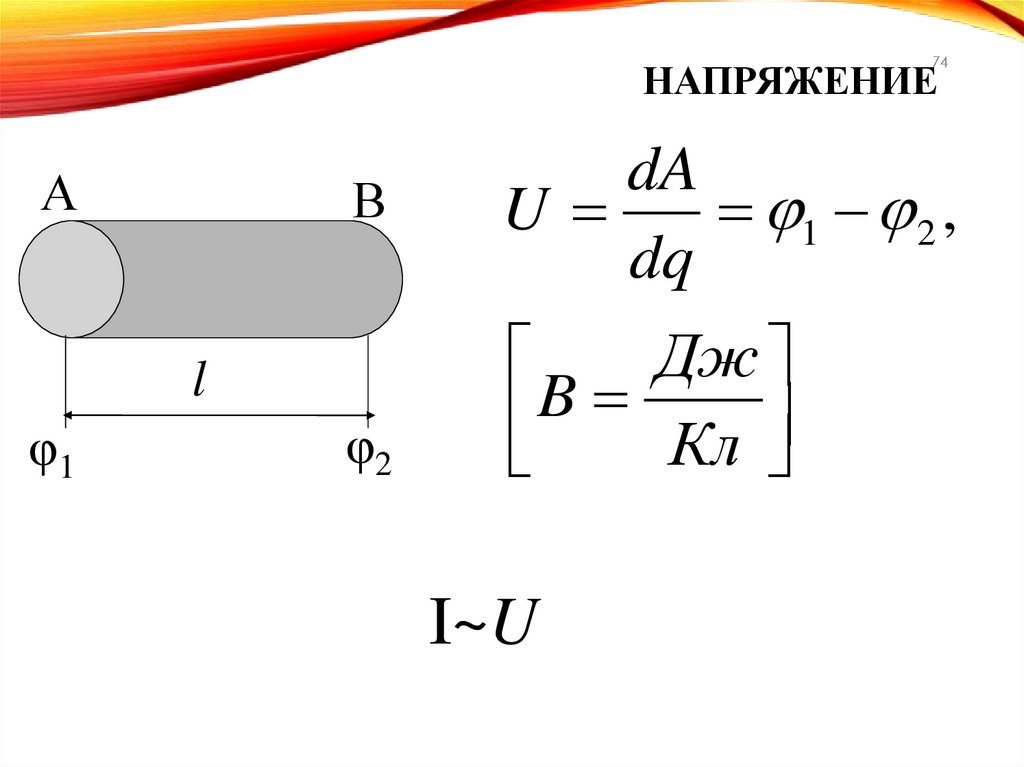
74НАПРЯЖЕНИЕ
А
В
l
φ1
φ2
dA
U
1 2 ,
dq
Дж
B
Кл
I~U
75.
75ЗАКОН ОМА В ИНТЕГРАЛЬНОЙ ФОРМЕ
(ДЛЯ ОДНОРОДНОГО УЧАСТКА ЦЕПИ)
U
I GU
R
76.
СОПРОТИВЛЕНИЕПРОВОДНИКА
l
R
S
1В
1
Ом
1А
76
77.
77УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ
Ом м
0 1 t
78.
78ЗАВИСИМОСТЬ
СОПРОТИВЛЕНИЯ МЕТАЛЛА ОТ
ТЕМПЕРАТУРЫ
R R0 1 t
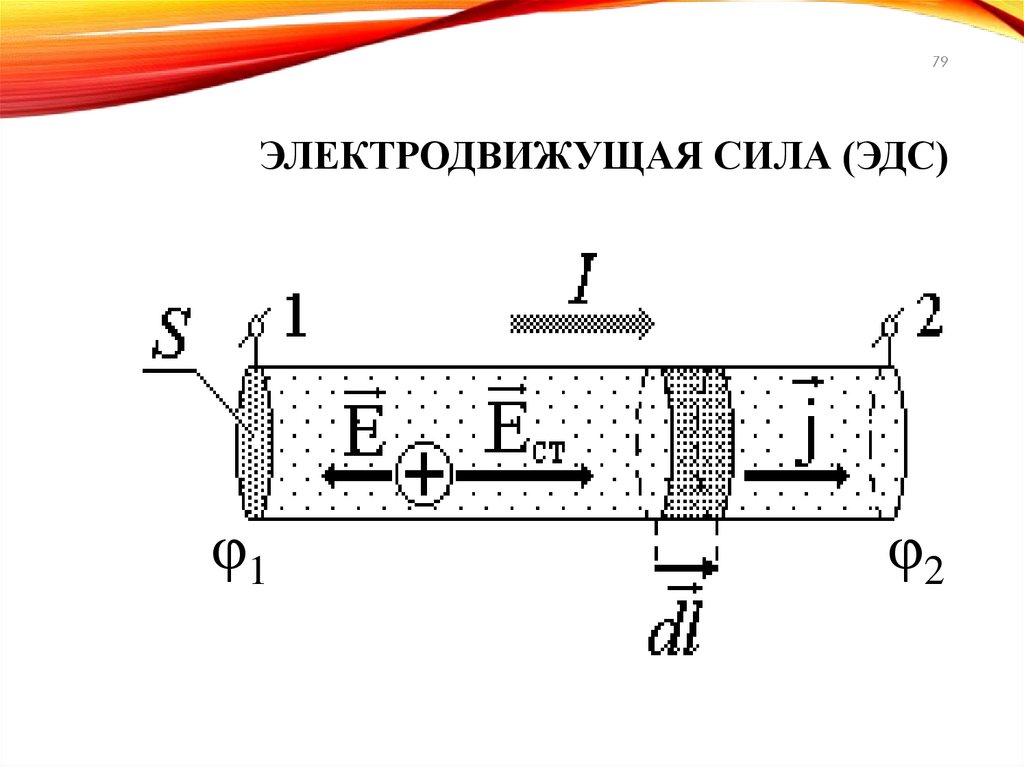
79.
79ЭЛЕКТРОДВИЖУЩАЯ СИЛА (ЭДС)
φ1
φ2
80.
80РАБОТА СТОРОННИХ СИЛ
2
Aстор Fстор dl q Eстор dl
2
l
l
81.
81ЭЛЕКТРОДВИЖУЩАЯ СИЛА
(ЭДС):
Aстор
q
Eстор dl
l
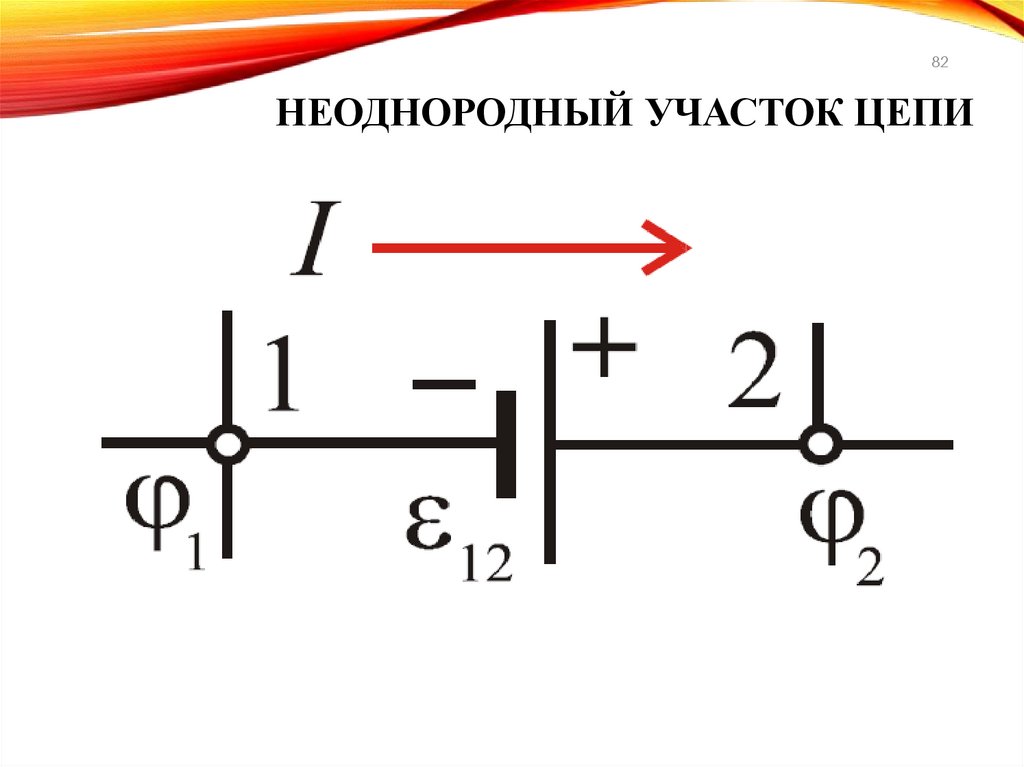
82.
82НЕОДНОРОДНЫЙ УЧАСТОК ЦЕПИ
83.
83A12 q Еэл dl q Ест dl
2
2
1
1
q( 1 2 ) q 12
q 12
84.
8412 Ест dl
2
1
85.
85A12
U
12
q
U 1 2
86.
861) при ε = 0,
U 1 2
2) при ε≠0, ε = U.
1
2
3) при U=0,
87.
ЗАКОН ОМА ВДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
ДЛЯ ОДНОРОДНОГО УЧАСТКА
ЦЕПИ:
87
j
1
E E
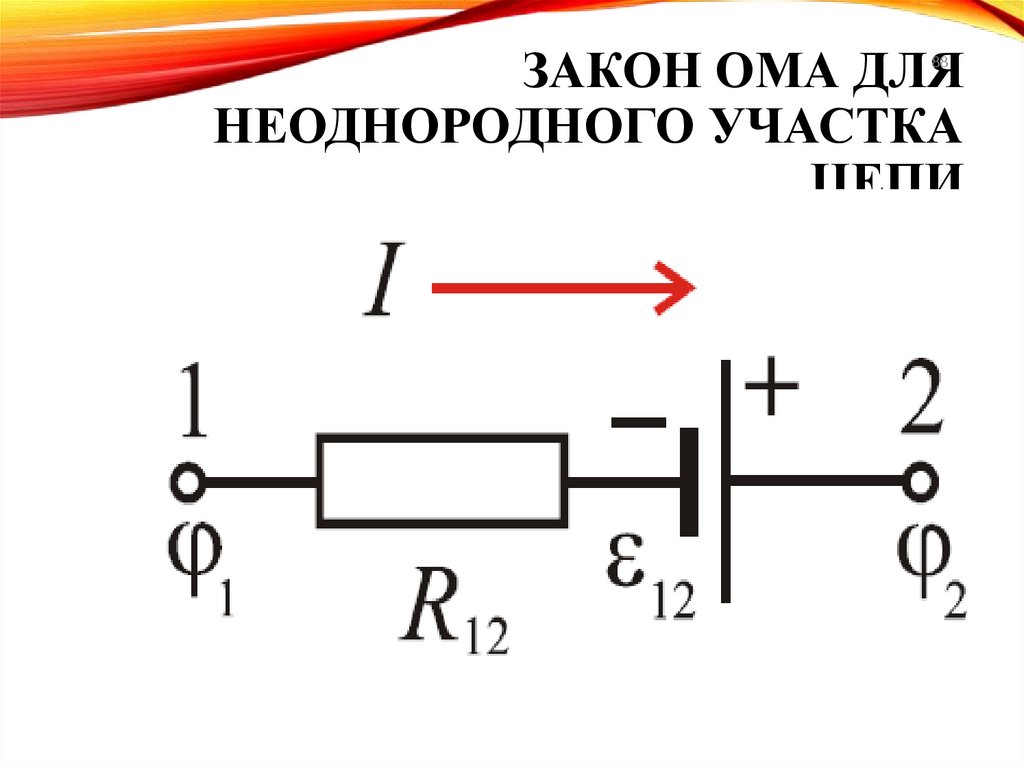
88.
ЗАКОН ОМА ДЛЯНЕОДНОРОДНОГО УЧАСТКА
ЦЕПИ
88
89.
IR12 1 2 12I
89
1 2 12
.
R
90.
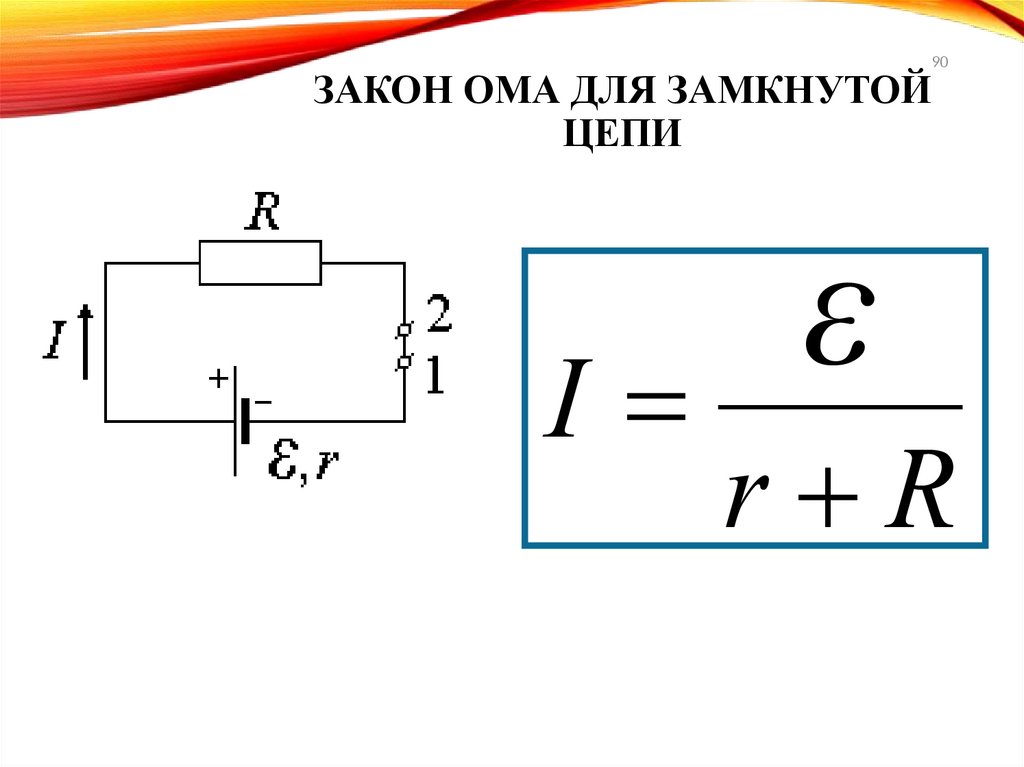
ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙЦЕПИ
ε
I
90
r R
91.
91ПОСЛЕДОВАТЕЛЬНОЕ И
ПАРАЛЛЕЛЬНОЕ
СОЕДИНЕНИЕ ПРОВОДНИКОВ
92.
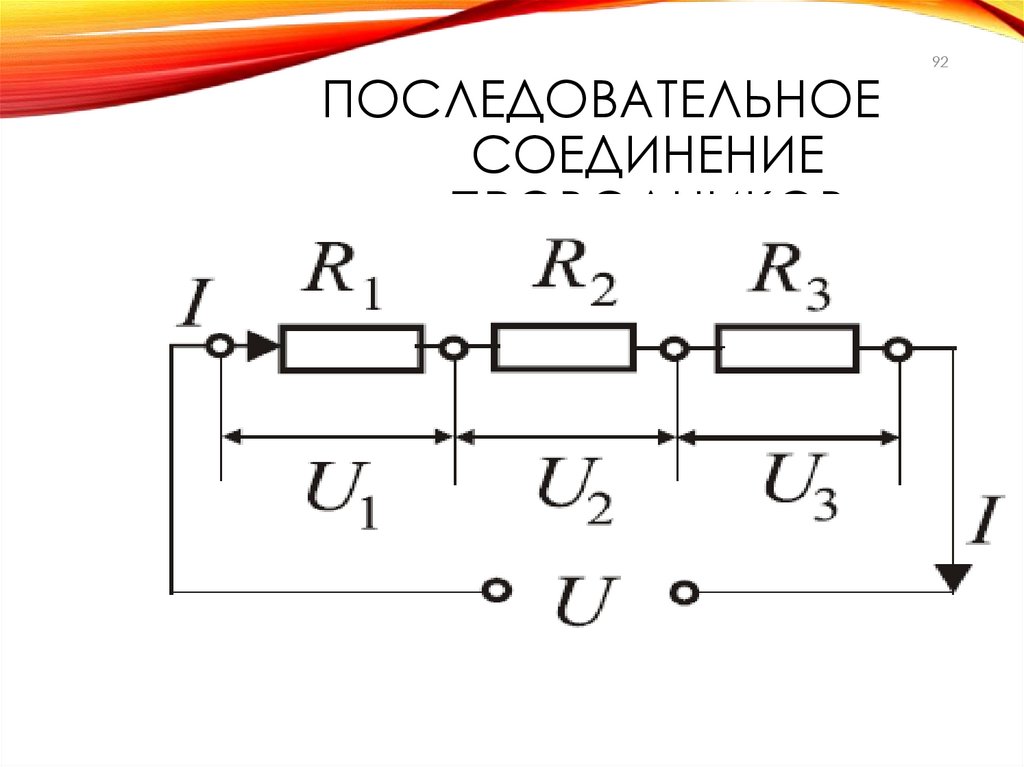
ПОСЛЕДОВАТЕЛЬНОЕСОЕДИНЕНИЕ
ПРОВОДНИКОВ
92
93.
93n
q
I const , U U i
t
i 1
n
U i
U i 1
R
I
I
n
R Ri
i 1
94.
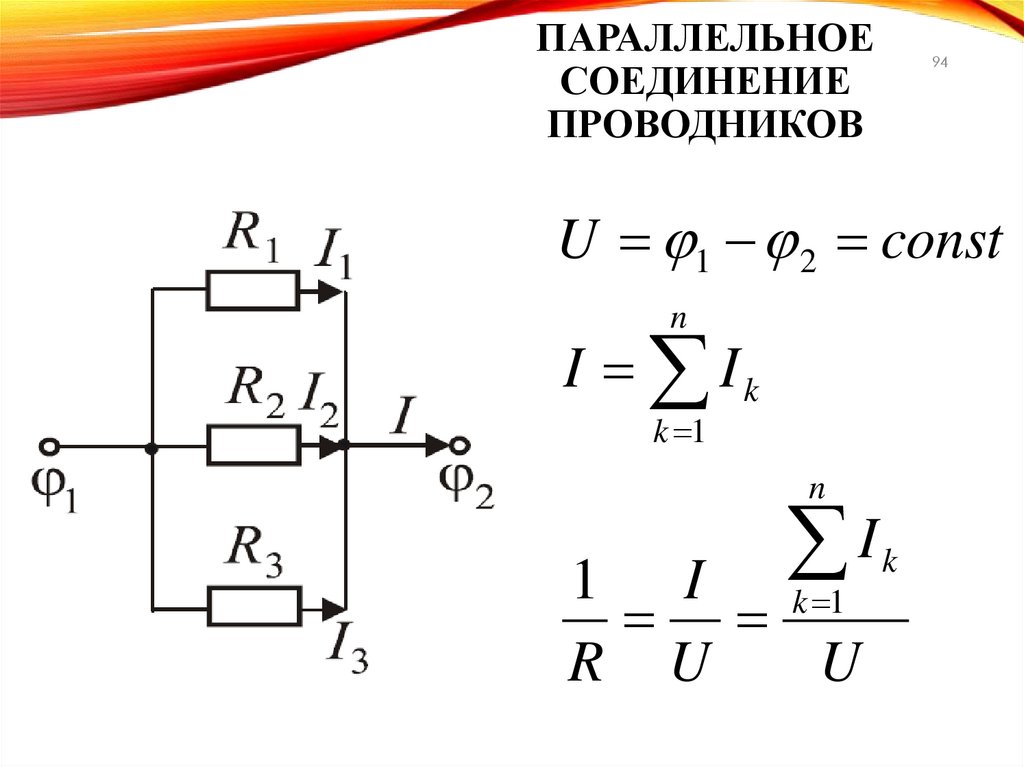
ПАРАЛЛЕЛЬНОЕСОЕДИНЕНИЕ
ПРОВОДНИКОВ
94
U 1 2 const
n
I Ik
k 1
n
I
1 I
k 1
R U
U
k
95.
Ik1
U Rk
n
1
1
R k 1 Rk
95
96.
96ПРАВИЛА КИРХГОФА.
ПРИМЕР РАСЧЕТА
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ.
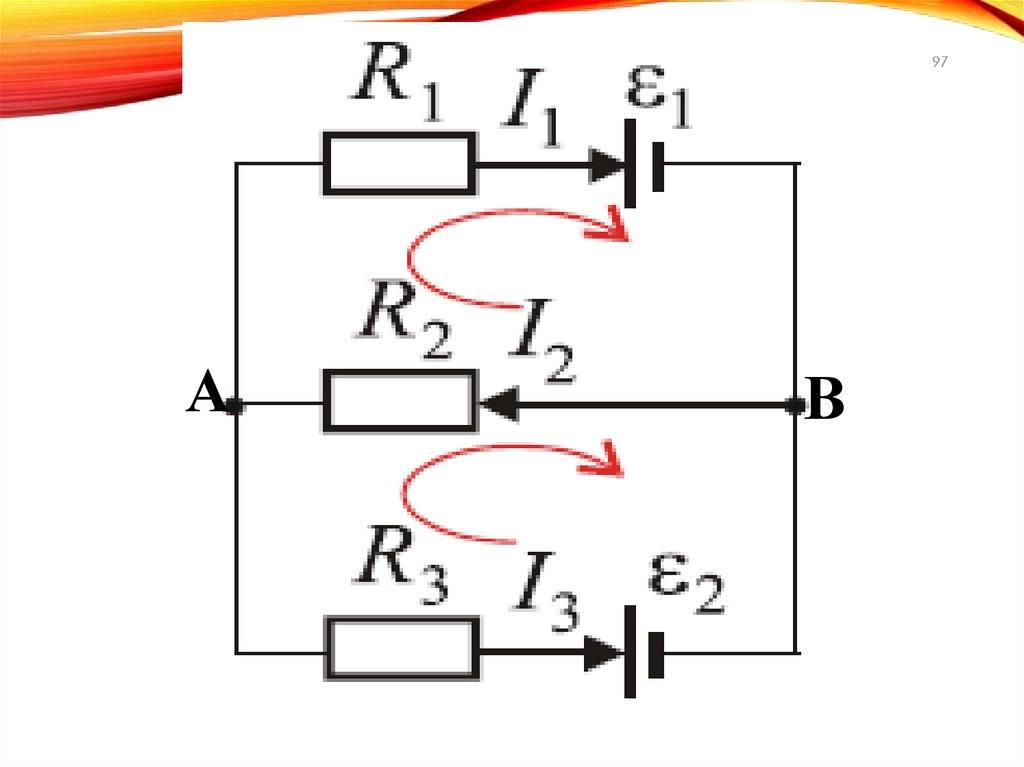
97.
97А
В
98.
98ПЕРВОЕ ПРАВИЛО КИРХГОФА
n
I
0
i
i 1
99.
99ВТОРОЕ ПРАВИЛО
КИРХГОФА
n
т
i 1
к 1
I
R
i i к
100.
100ПОРЯДОК РАСЧЕТА СЛОЖНОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА:
1) произвольно выбрать и обозначить на
чертеже направления токов на всех участках
цепи;
2) подсчитать число узлов m и записать первое
правило Кирхгофа для всех m – 1 узлов.
3) выделить произвольные замкнутые контуры
в цепи и условившись о направлении обхода
записать для них второе правило Кирхгофа
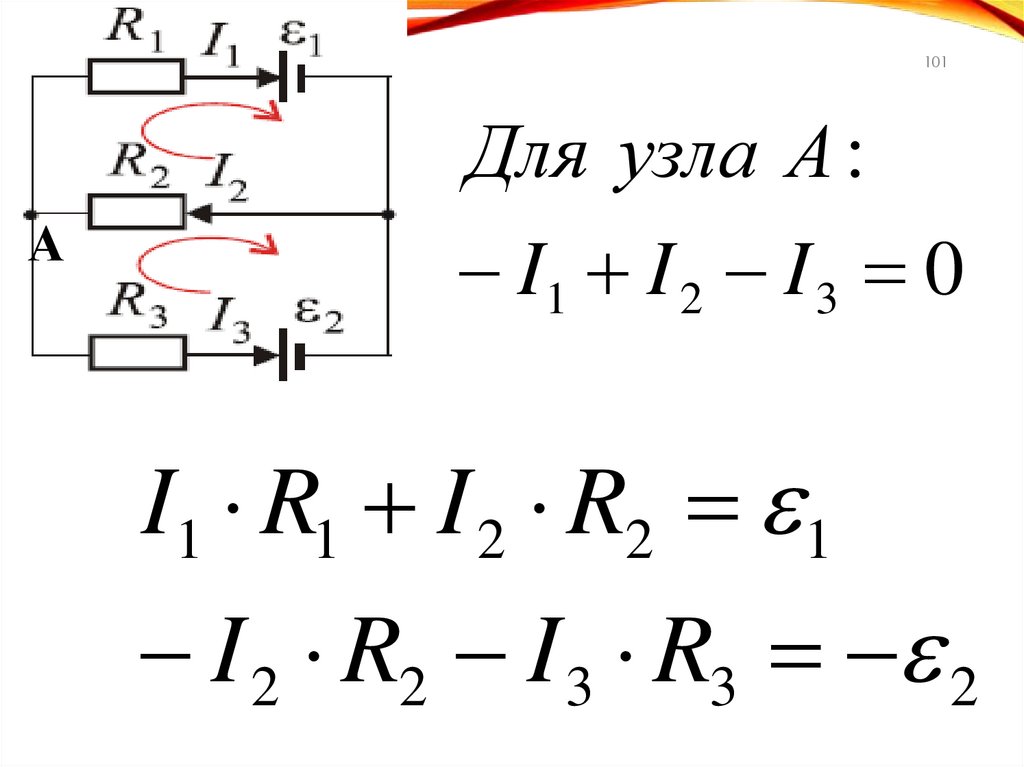
101.
101А
Для узла А :
I1 I 2 I 3 0
I1 R1 I 2 R2 1
I 2 R2 I 3 R3 2
102.
102РАБОТА И МОЩНОСТЬ
ТОКА.
ЗАКОН ДЖОУЛЯ-ЛЕНЦА
103.
103РАБОТА И МОЩНОСТЬ ТОКА
R
1
φ1
I
2
φ2
U12 1 2
q=I·t
104.
А 1 2 q U12 q U12 I t2
12
104
U
A I U12 t I R t
t
R
2
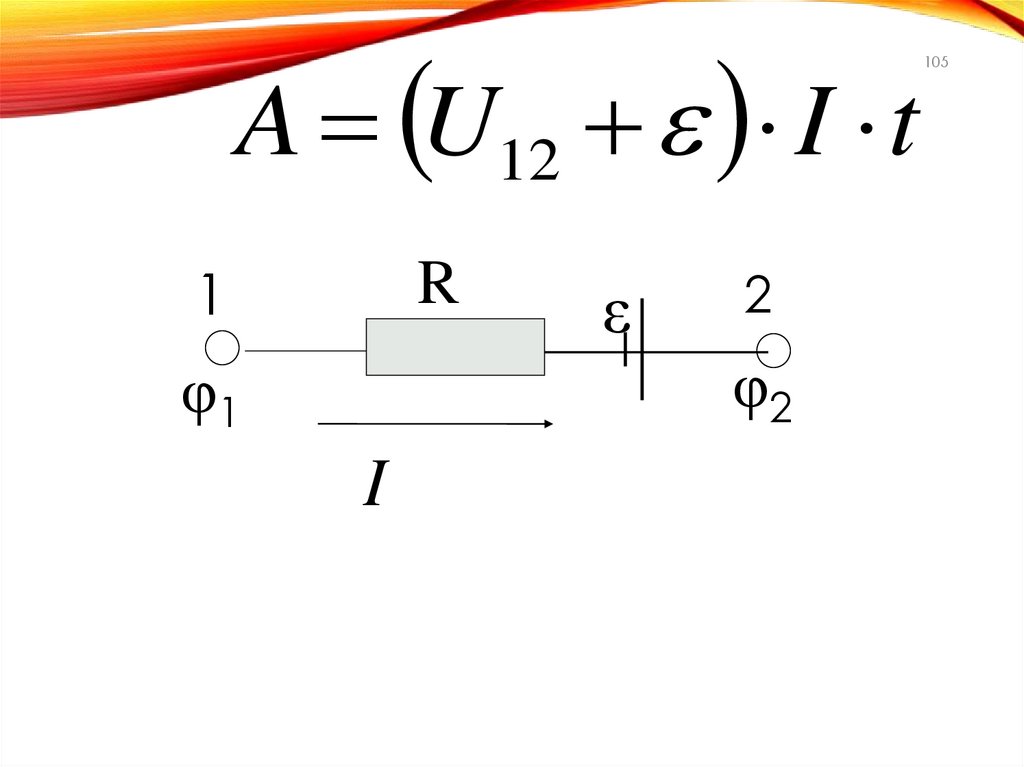
105.
A U12 I t1
R
ε
2
φ2
φ1
I
105
106.
U12 1 2 0106
A I t
А I Rполн t
2
107.
AP
t
107
МОЩНОСТЬ ТОКА:
Для неоднородного
участка цепи:
Для полной цепи:
P I U12 I
Pполн I
Мощность, выделяемая во внешней цепи:
2
U
Рвнеш I U I R
R
2
108.
108ЗАКОН ДЖОУЛЯЛЕНЦА
dQ dA U I dt
2
U
2
I R dt
dt
R
109.
109ЗАКОН ДЖОУЛЯ-ЛЕНЦА В
ИНТЕГРАЛЬНОЙ ФОРМЕ:
t
Q I R dt
2
0
110.
ЗАКОН ДЖОУЛЯ-ЛЕНЦА ВДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
110
E
2
E
2











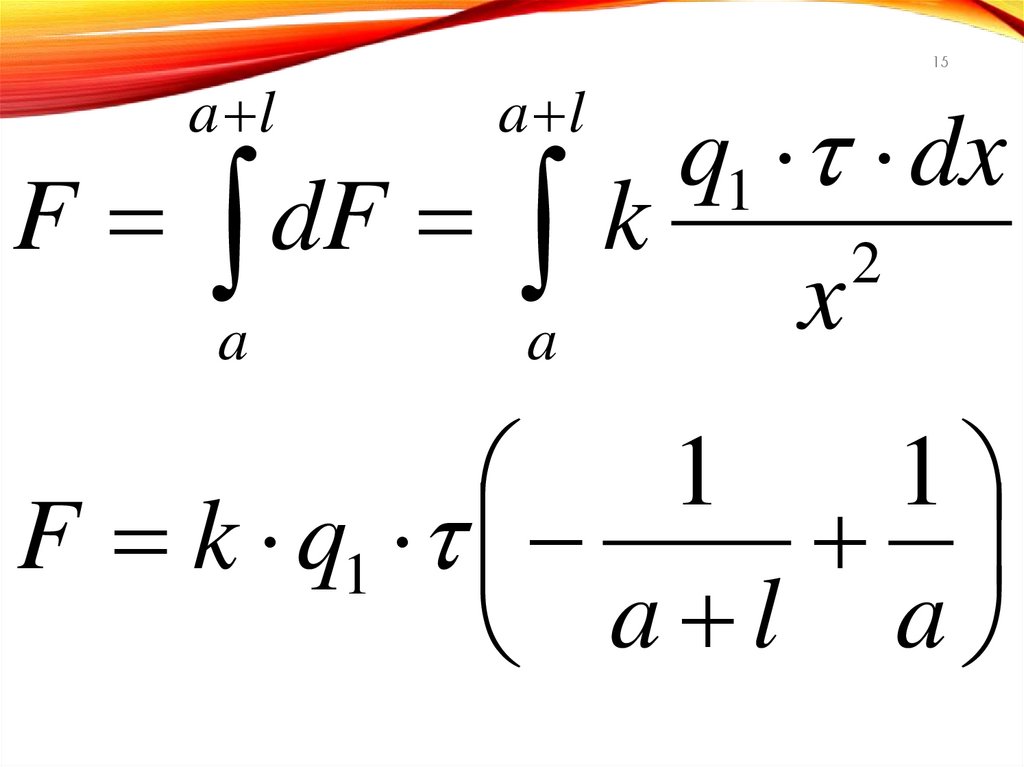






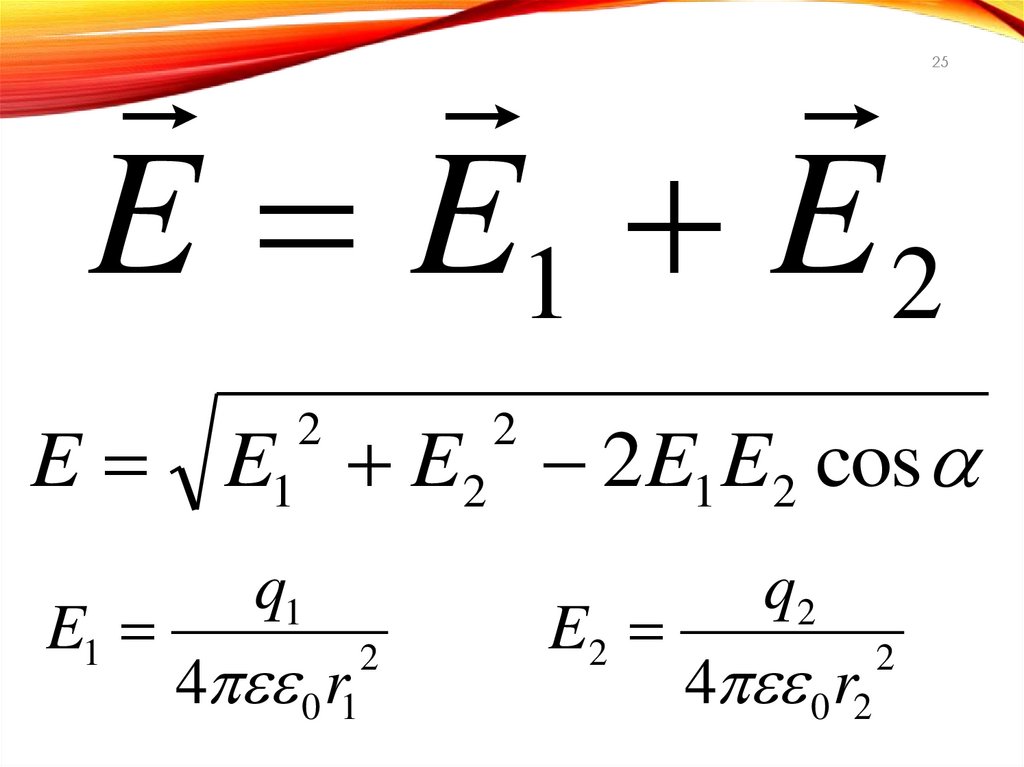
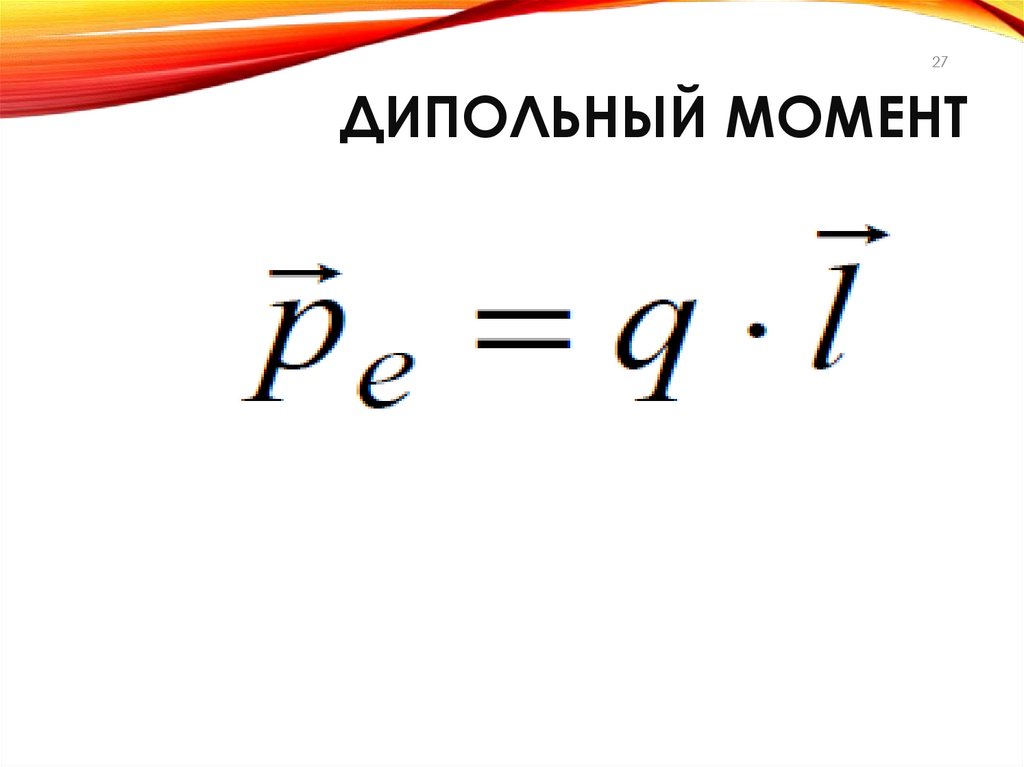


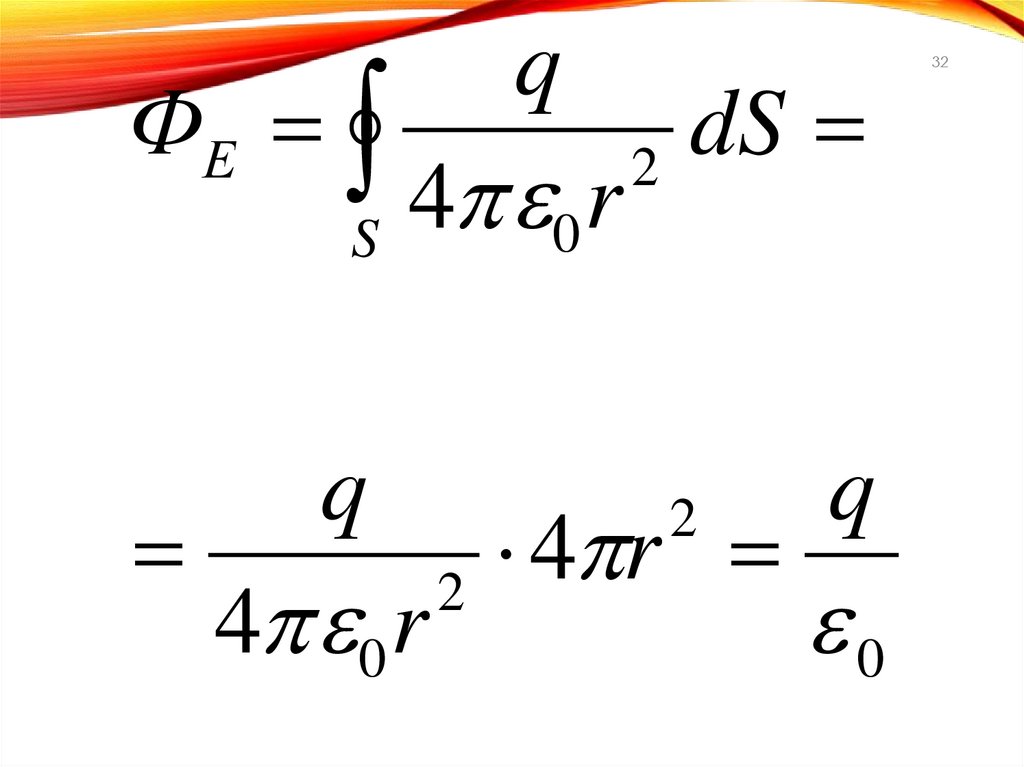




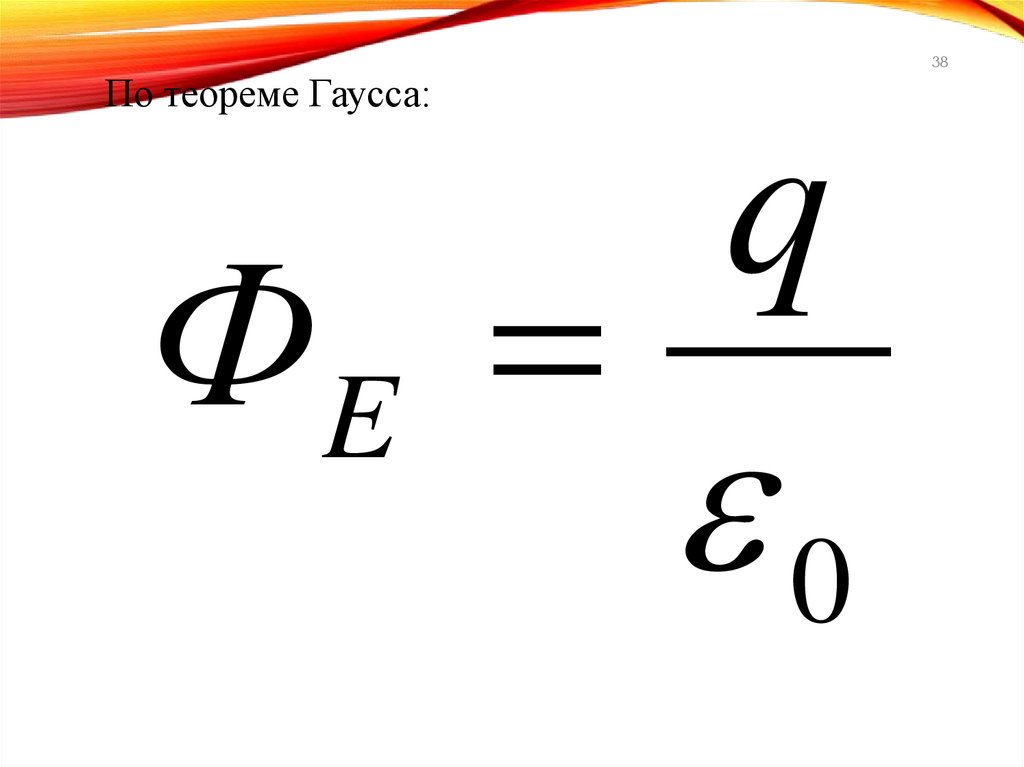
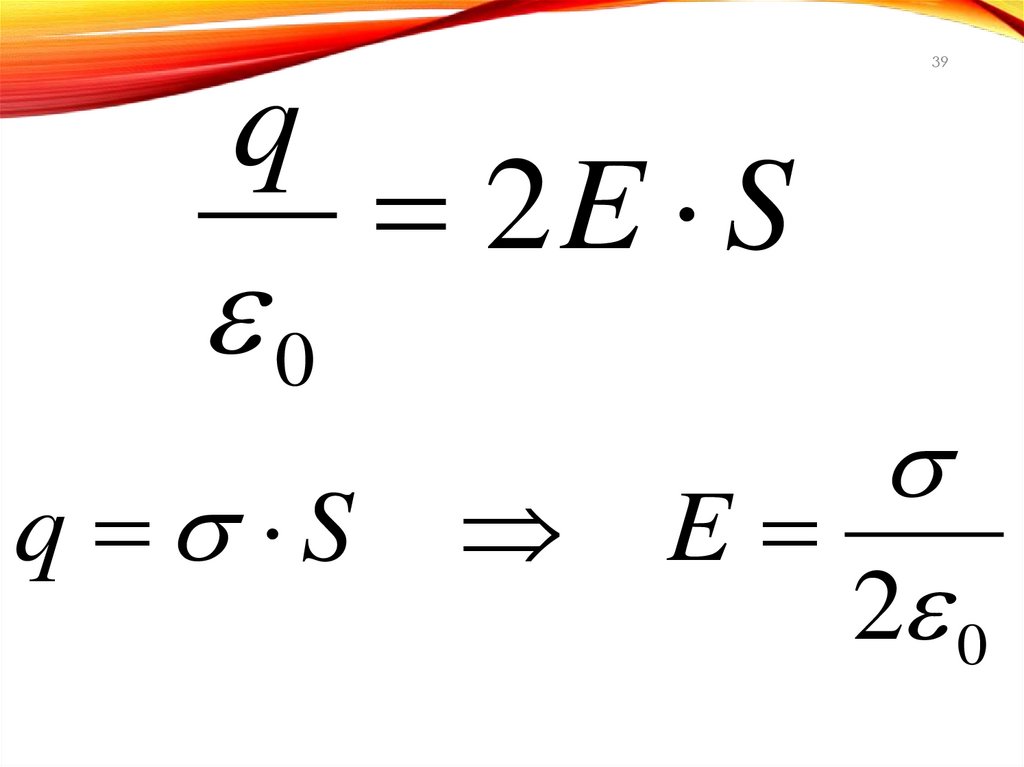






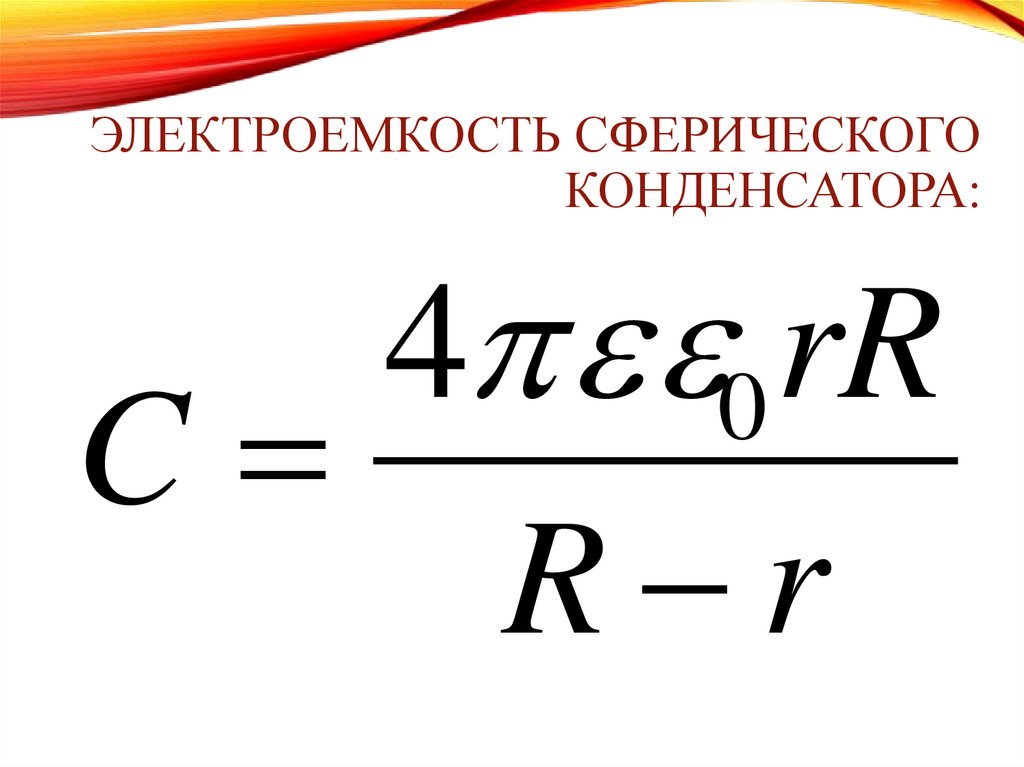


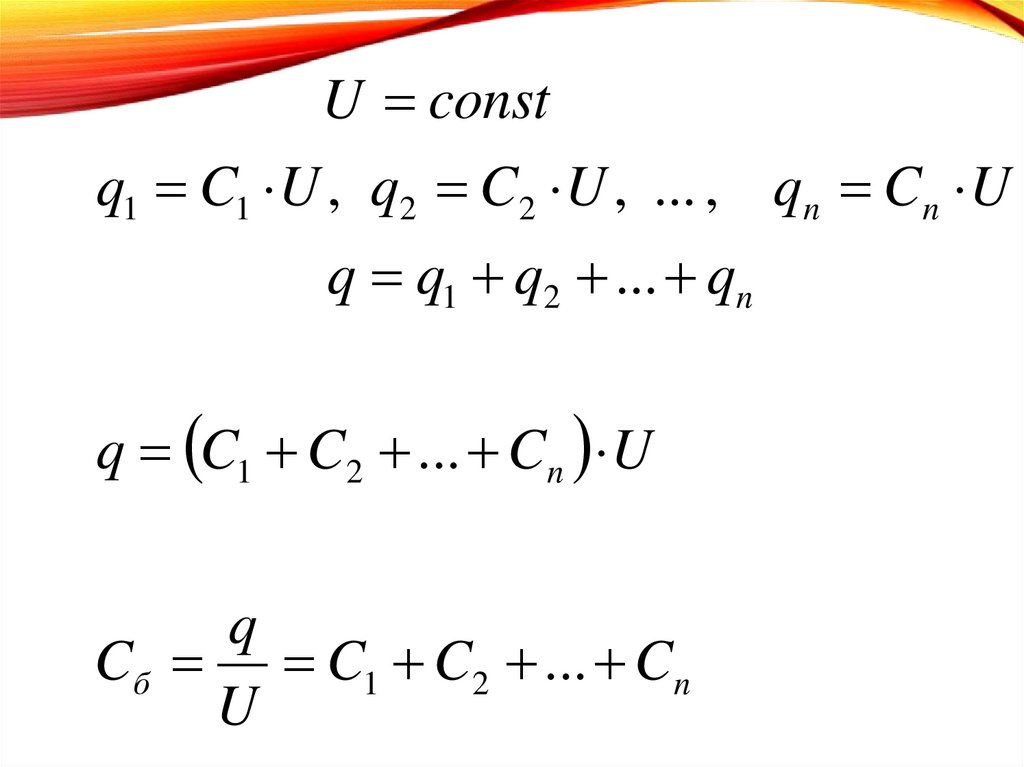

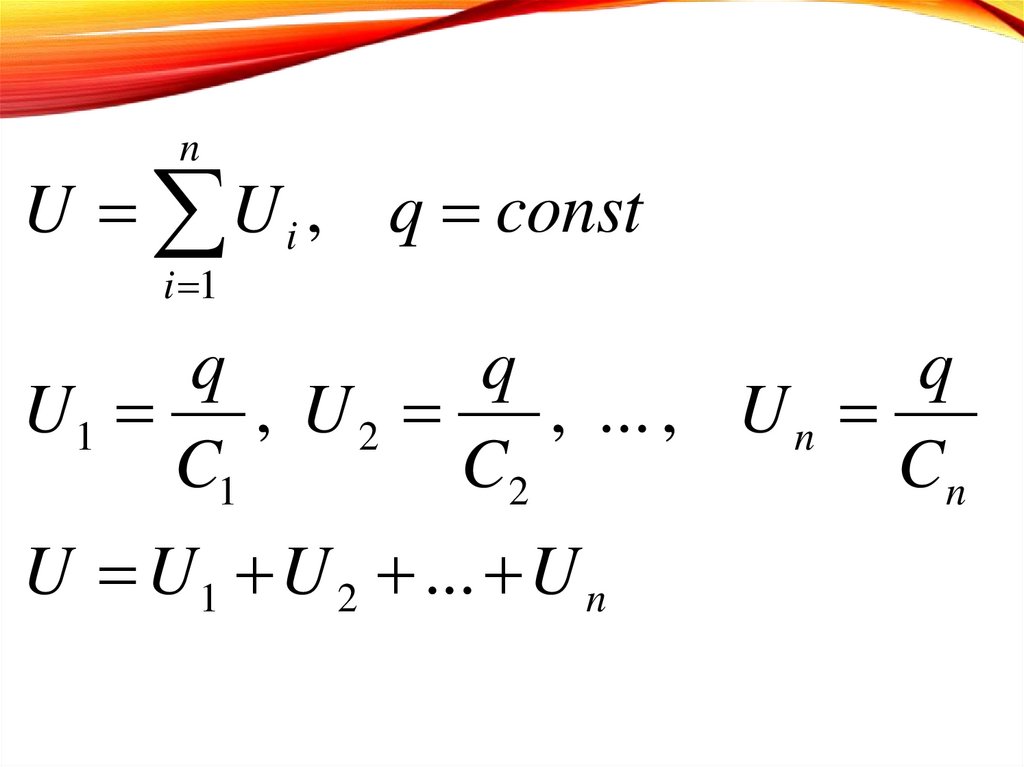
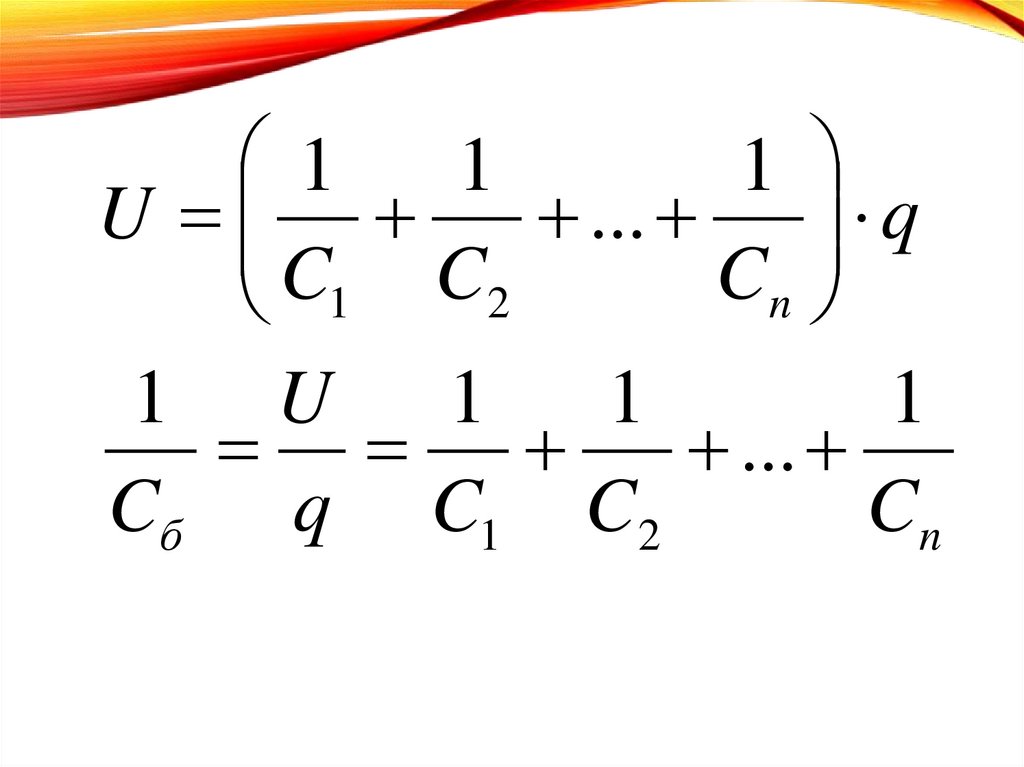

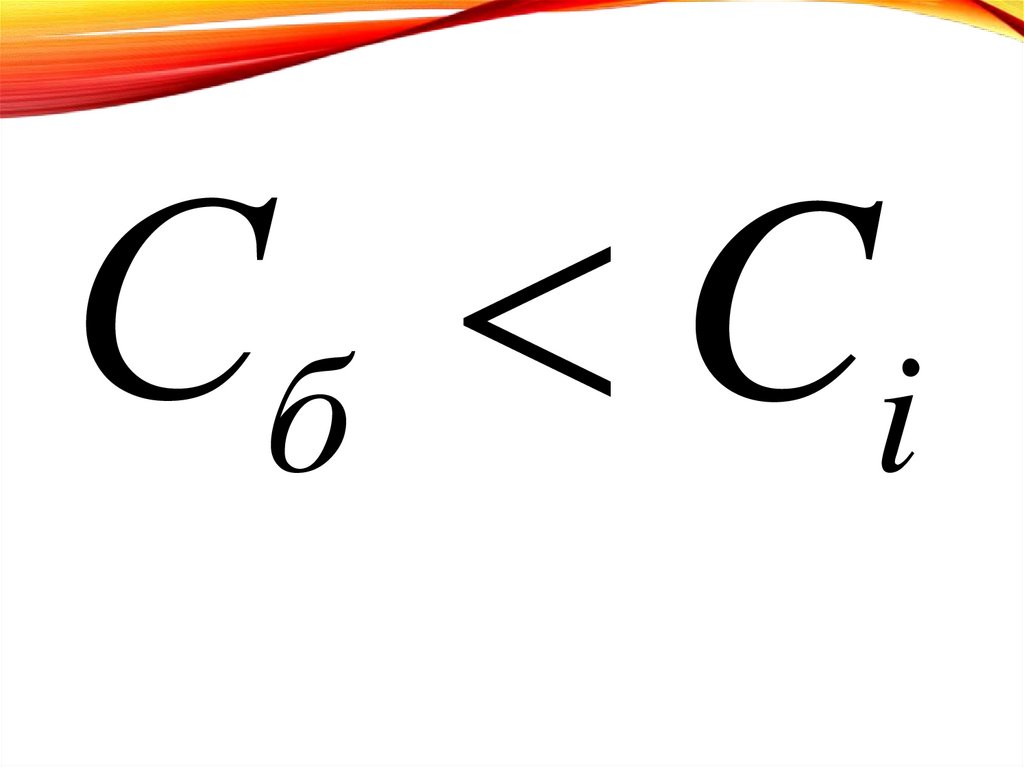











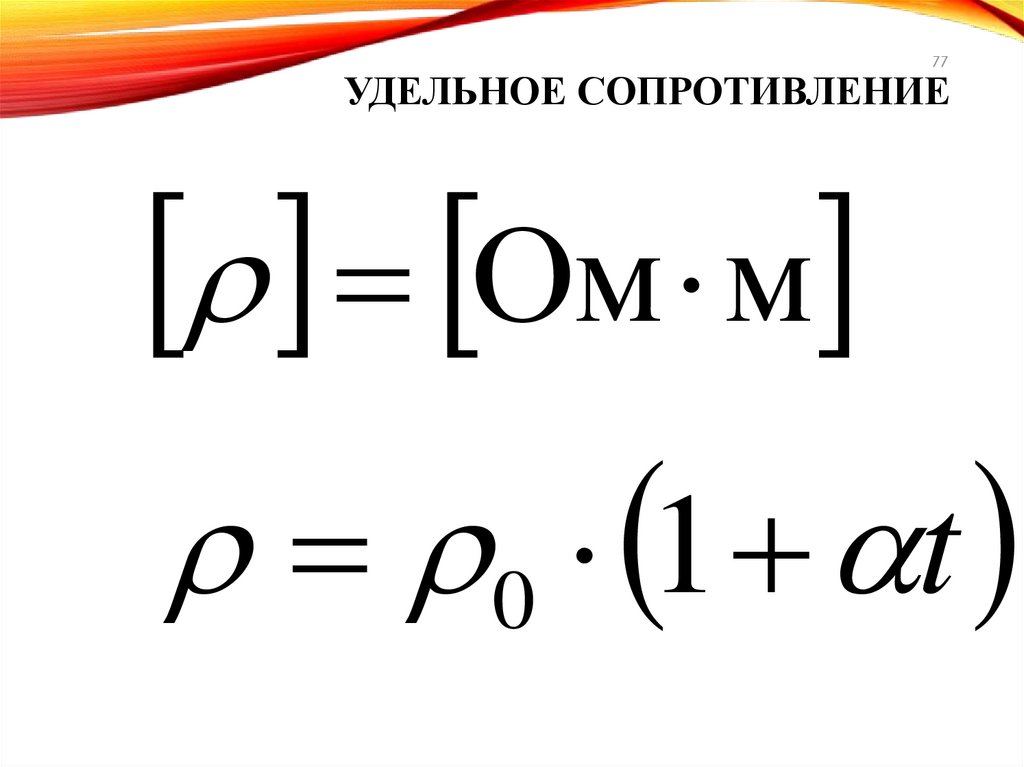




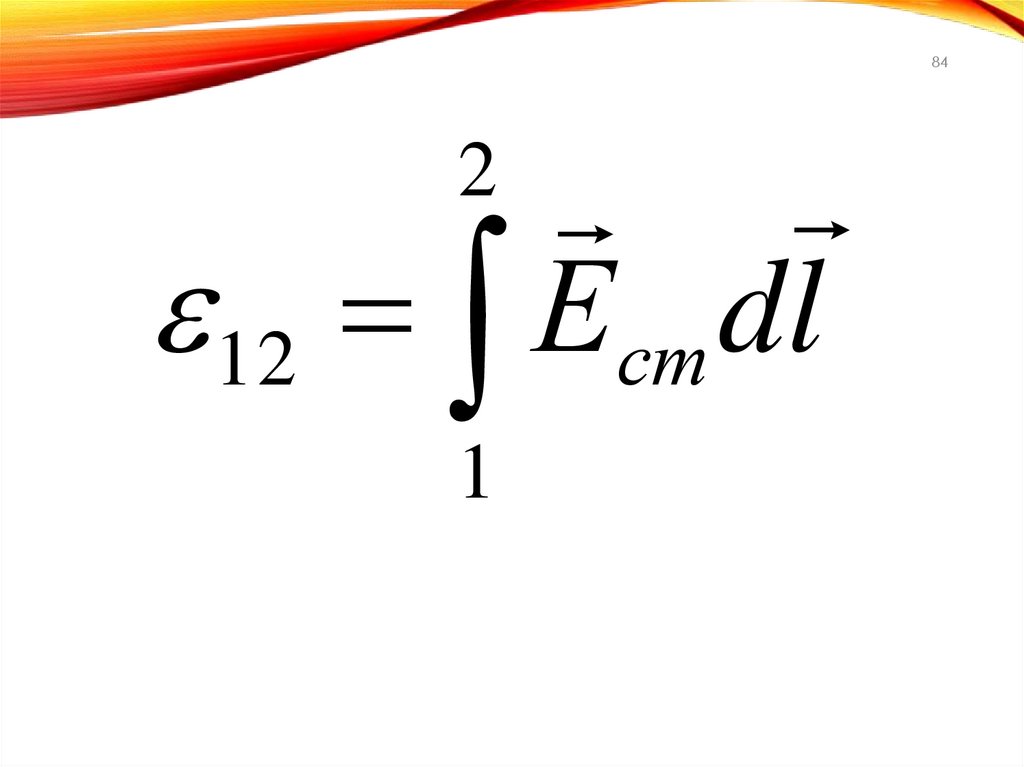
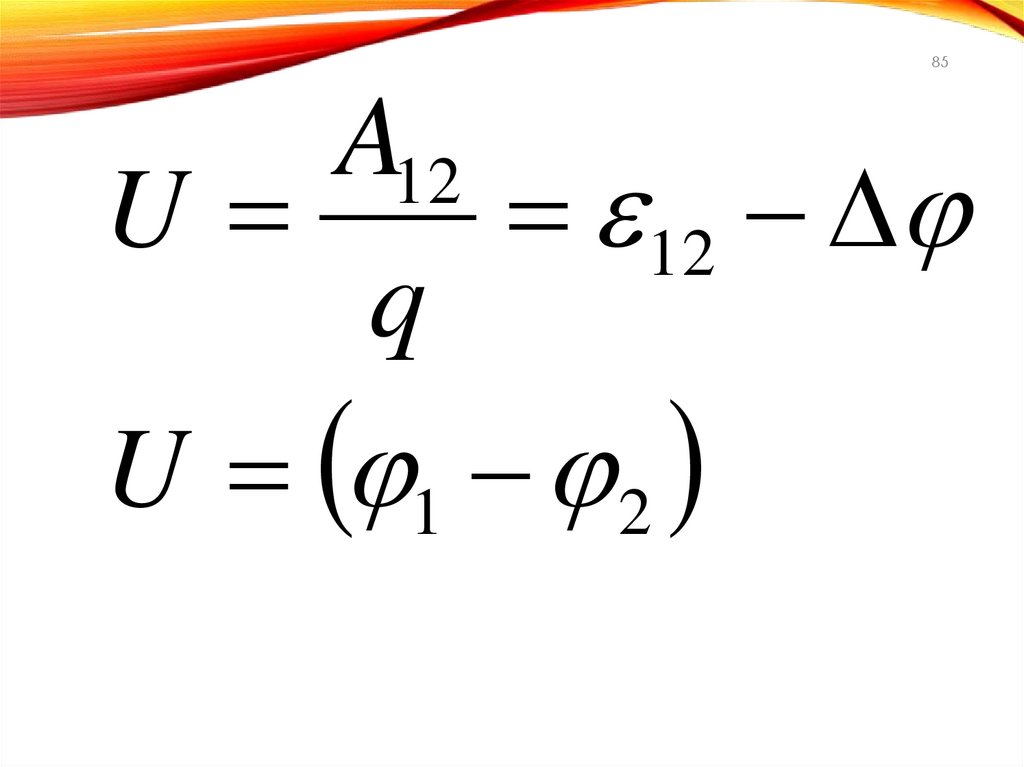
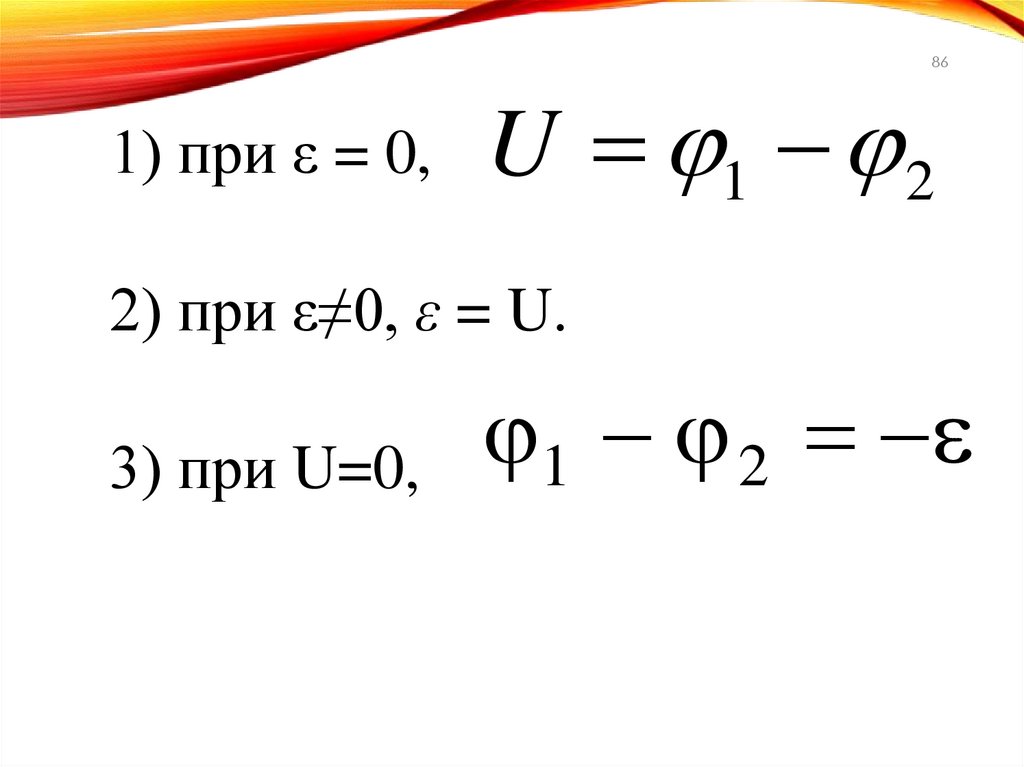

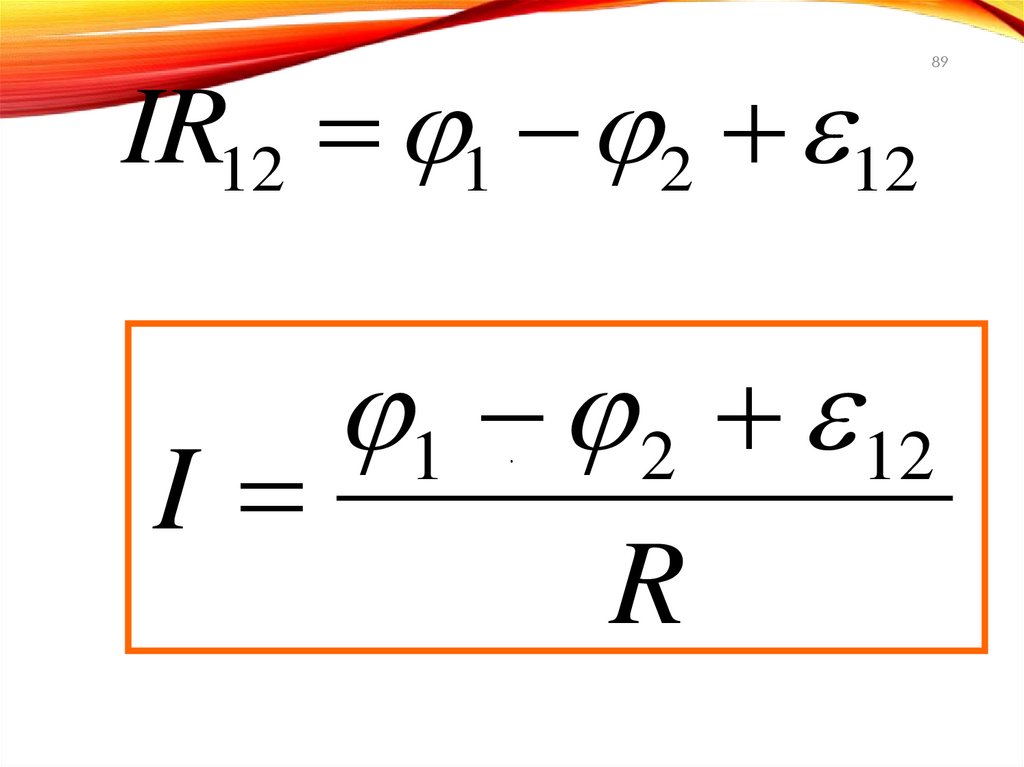


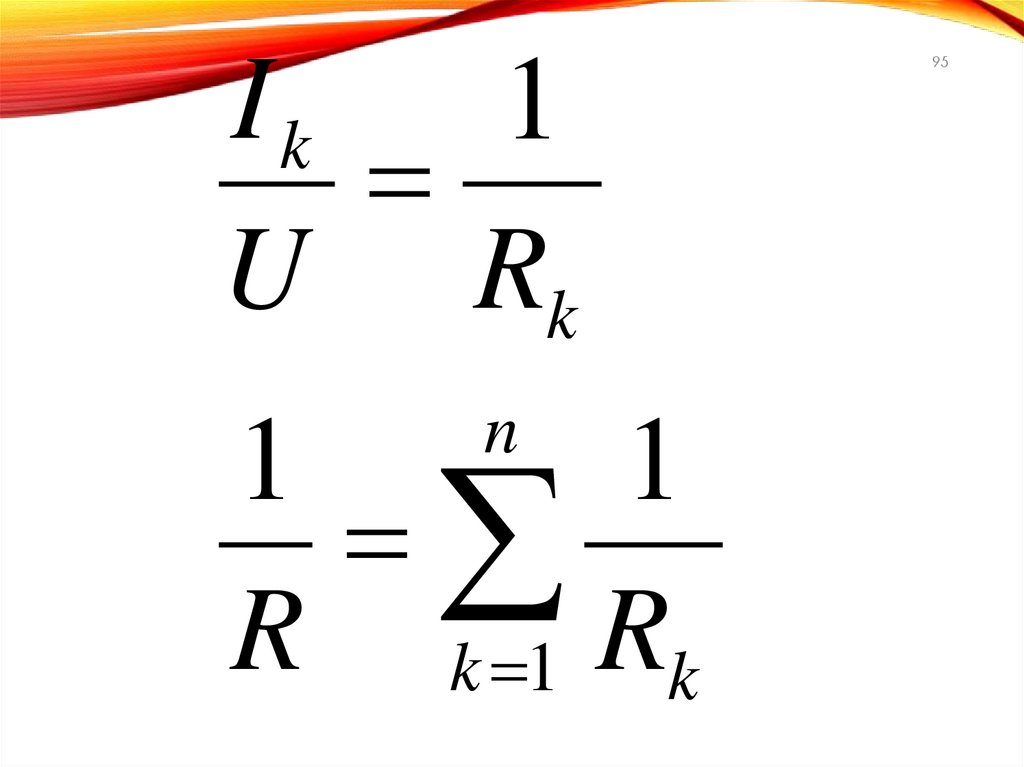

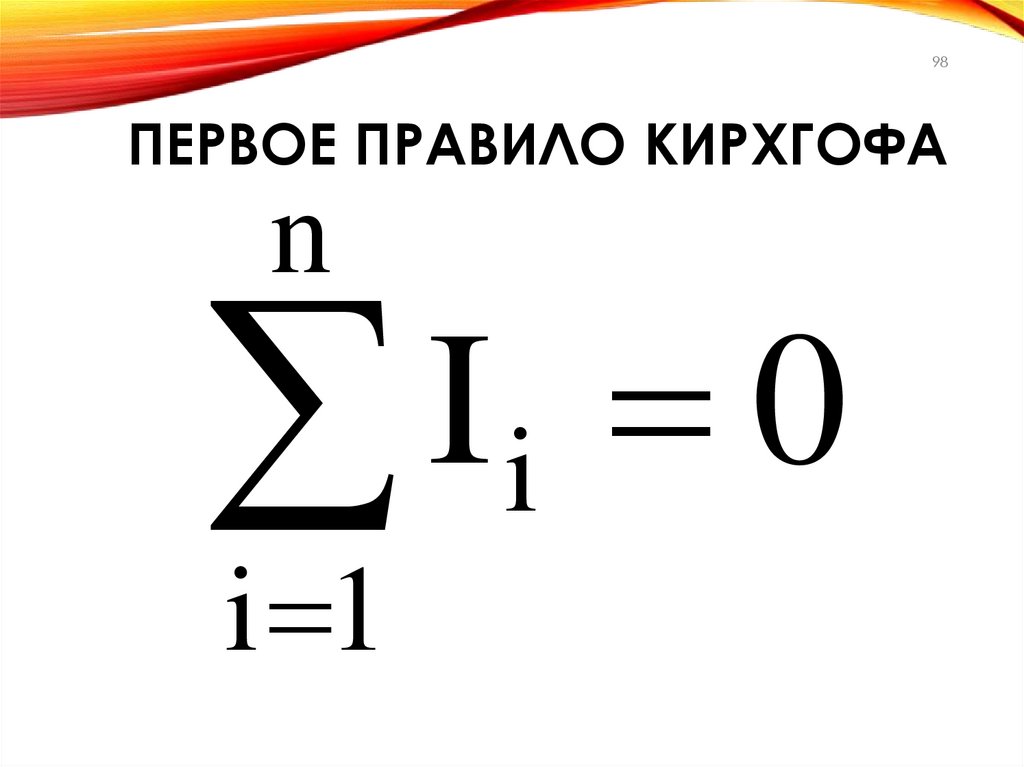




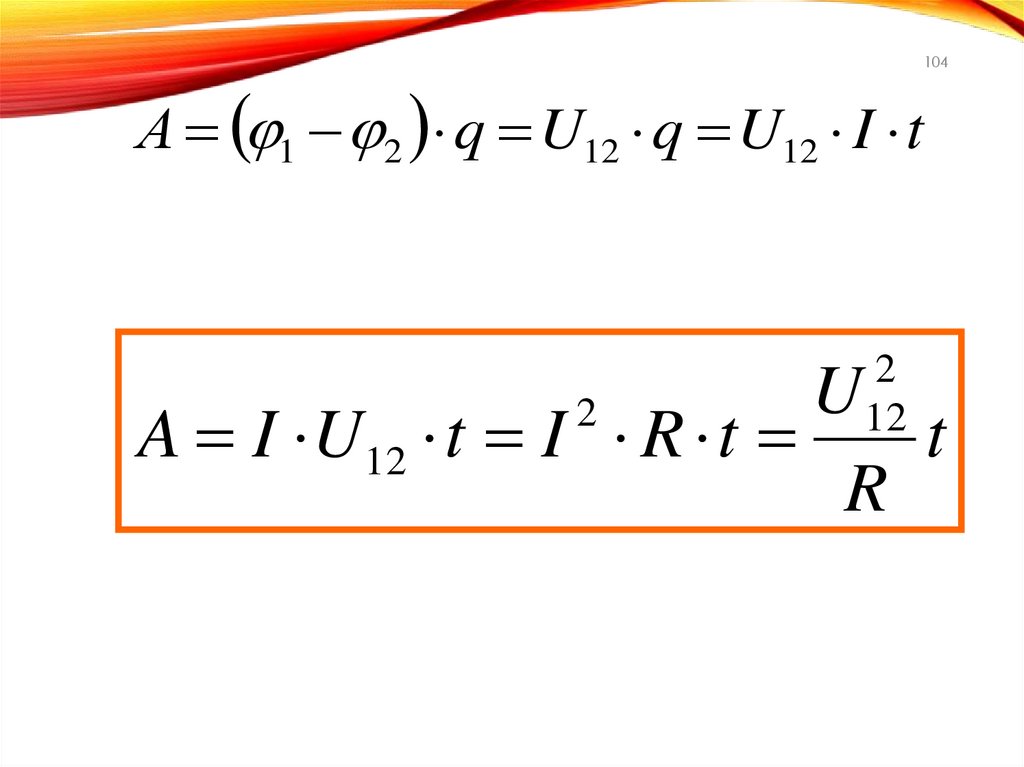





 physics
physics








