Similar presentations:
Электростатика. Постоянный ток
1.
МИНОБРНАУКИ РОССИИФедеральное государственное бюджетное образовательное учреждение
высшего образования
«Оренбургский государственный университет»
Электростатика
Постоянный ток
Манаков Н.А., Гуньков В.В.
Оренбург
2018
2.
Оглавление1. Закон сохранения электрического заряда. Закон Кулона
2. Напряженность электростатического поля. Принцип
суперпозиции. Поле диполя
3. Теорема Гаусса Циркуляция вектора напряженности
4. Потенциал электростатического поля
5. Электростатическое поле в диэлектрике
6. Проводники в электростатическом поле Электроёмкость
7. Постоянный электрический ток. Закон Ома. Сопротивление
8. Электрические цепи постоянного тока
9. Токи в различных средах
10. Работа выхода электронов из металла Эмиссионные явления
11. Список использованных источников
3.
Закон сохраненияэлектрического заряда
Закон Кулона
Лекция 1
4.
Закон сохранения электрического зарядаНесмотря на огромное разнообразие веществ в
природе, существует только два типа электрических
зарядов:
заряды, подобные возникающим на стекле, потертом
о кожу (их назвали положительными),
и заряды, подобные возникающим на эбоните,
потертом о мех (их назвали отрицательными);
одноименные заряды друг от друга отталкиваются,
разноименные — притягиваются.
5.
• Опытным путем (1910—1914) американский физикР. Милликен показал, что электрический заряд
дискретен, т. е. заряд любого тела составляет
целое кратное от элементарного электрического
заряда е (е = 1,6 10-19 Кл).
• Электрон (9,11 10-31 кг) и протон (1,67 10-27 кг)
являются соответственно носителями
элементарных отрицательного и положительного
зарядов.
Все тела в природе способны электризоваться, т. е.
приобретать электрический заряд.
Электризация тел может осуществляться
различными способами: соприкосновением
(трением), электростатической индукцией и т.д.
6.
• Из обобщения опытных данных был установленфундаментальный закон природы,
экспериментально подтвержденный в 1843 г.
английским физиком М. Фарадеем,— закон
сохранения заряда:
• алгебраическая сумма электрических зарядов
любой замкнутой системы (системы, не
обменивающейся зарядами с внешними телами)
остается неизменной, какие бы процессы ни
происходили внутри этой системы.
• Электрический заряд — величина релятивистски
инвариантная, т. е. не зависит от системы отсчета,
а значит, не зависит от того, движется этот заряд
или покоится.
7.
• В зависимости от концентрации свободныхзарядов тела делятся на проводники, диэлектрики
и полупроводники.
• Проводники — тела, в которых электрический
заряд может перемещаться по всему его объему.
Проводники делятся на две группы:
• 1) проводники первого рода (металлы) —
перенесение в них зарядов (свободных
электронов) не сопровождается химическими
превращениями;
• 2) проводники второго рода (например,
расплавленные соли, растворы кислот) —
перенесение в них зарядов (положительных и
отрицательных ионов) ведет к химическим
изменениям.
8.
• Диэлектрики (например, стекло,пластмассы) — тела, в которых практически
отсутствуют свободные заряды.
• Полупроводники (например, германий,
кремний) занимают промежуточное
положение между проводниками и
диэлектриками.
• Единица электрического заряда
(производная единица, так как определяется
через единицу силы тока) - кулон (Кл) электрический заряд, проходящий через
поперечное сечение проводника при силе
тока 1 А за время 1 с.
9.
Закон Кулона• Точечным называется заряд, сосредоточенный на
теле, линейные размеры которого пренебрежимо
малы по сравнению с расстоянием до других
заряженных тел, с которыми он взаимодействует.
• Понятие точечного заряда, как и материальной
точки, является физической абстракцией.
• Закон взаимодействия неподвижных точных
электрических зарядов установлен в 1785 г. Ш.
Кулоном с помощью крутильных весов.
10.
Закон Кулона: сила взаимодействия F междудвумя неподвижными точечными зарядами,
находящимися в вакууме, пропорциональна
зарядам Q1 и Q2 и обратно пропорциональна
квадрату расстояния r между ними:
Q1Q2
F k 2 ,
r
• где k — коэффициент пропорциональности,
зависящий от выбора системы единиц.
11.
• Сила F направлена по прямой, соединяющейвзаимодействующие заряды, т. е. является
центральной, и соответствует
• притяжению (F < 0) в случае разноименных
зарядов и
• отталкиванию (F > 0) в случае одноименных
зарядов.
• Эта сила называется кулоновской силой.
• В векторной форме закон Кулона имеет вид
Q1Q2 r12
F12 k 2
r
r
(1.1)
12.
• В СИ коэффициент пропорциональности равенk 1 /(4 0 ) .
F12
r12
Q1>0
F21
Q2>0
Рисунок 1
• Взаимодействие электрических точечных зарядов
удовлетворяет третьему закону Ньютона
F21 F12
13.
• В окончательном виде закон Кулона запишется:1 Q1Q2
F
.
2
4 0 r
(1.2)
Величина 0 называется электрической постоянной;
она относится к числу фундаментальных
физических постоянных и равна
8,85 10-12Кл2/(Н м2), или
0 8,85 10 12 Ф / м ,
(1.3)
где фарад (Ф) — единица электрической емкости.
1 /(4 0 ) 9 109 м / Ф .
14.
Напряженностьэлектростатического поля
Принцип суперпозиции
электростатических полей
Поле диполя
Лекция 2
15.
Электростатическое поле. Напряженностьэлектростатического поля
• Если в пространство, окружающее электрический
заряд, внести другой заряд, то на него будет
действовать кулоновская сила; значит, в
пространстве, окружающем электрические заряды,
существует силовое поле.
• Мы будем рассматривать электрические поля,
которые создаются неподвижными электрическими
зарядами и называются электростатическими.
• Для обнаружения и опытного исследования
электростатического поля используется пробный
точечный положительный заряд — такой заряд,
который не искажает исследуемое поле (не
вызывает перераспределения зарядов, создающих
поле).
16.
• Если в поле, создаваемое зарядом Q, поместитьпробный заряд Q0, то на него действует сила F ,
различная в разных точках поля, которая, согласно
закону Кулона (1.2), пропорциональна пробному
заряду Q0.
• Поэтому отношение F / Q0 не зависит от Q0 и
характеризует электрическое поле в той точке, где
пробный заряд находится.
• Эта величина называется напряженностью и
является силовой характеристикой
электростатического поля.
17.
• Напряженность электростатического поля вданной точке есть физическая величина,
определяемая силой, действующей на единичный
положительный заряд, помещенный в эту точку
поля:
(1.4)
E F / Q0 .
• Как следует из формул (1.4) и (1.1), напряженность
поля точечного заряда в вакууме
• E
1 Q r или
1
Q
,
E
.
2
2
4 0 r r
4 0 r
(1.5)
• Направление вектора E совпадает с направлением силы,
действующей на положительный заряд.
18.
Q+
E
Q
E
A
A
-
Рисунок 2
19.
• Из формулы (1.4) следует, что единицанапряженности электростатического поля —
ньютон на кулон (Н/Кл).
• 1 Н/Кл — напряженность такого поля, которое на
точечный заряд в 1 Кл действует с силой в 1 Н;
• 1 Н/Кл = 1 В/м, где В (вольт) — единица
потенциала электростатического поля.
• Графически электростатическое поле изображают
с помощью линий напряженности — линий,
касательные к которым в каждой точке совпадают
с направлением вектора (рис. 3).
• Линиям напряженности приписывается
направление, совпадающее с направлением
вектора напряженности.
20.
1Е1
2
Е2
Рисунок 3
• Чтобы с помощью линий напряженности можно было характеризовать
не только направление, но и значение напряженности
электростатического поля, условились проводить их с определенной
густотой: число линий напряженности, пронизывающих единицу
площади поверхности, перпендикулярную линиям напряженности,
должно быть равно модулю вектора напряженности.
21.
• Для однородного поля вектор напряженности влюбой точке постоянен по величине и
направлению, а линии напряженности
параллельны вектору напряженности.
• Если поле создается точечным зарядом, то линии
напряженности — радиальные прямые,
выходящие из заряда, если он положителен (рис.
4, а), и входящие в него, если заряд отрицателен
(рис. 4, б).
22.
а)б)
Рисунок 4
23.
• ВеличинаdФE En dS E dS
• называется потоком вектора напряженности
через площадку dS.
dS dS n
Е
dS
α
n
En
Рисунок 5
24.
• Единица потока вектора напряженностиэлектростатического поля - 1 В м.
• Для произвольной замкнутой поверхности S поток
вектора через эту поверхность
ФE En dS E dS ,
S
(1.6)
S
• Для замкнутых поверхностей за положительное
направление нормали принимается внешняя
нормаль, т. е. нормаль, направленная наружу
области, охватываемой поверхностью.
25.
Принцип суперпозицииэлектростатических полей. Поле диполя
• Рассмотрим метод определения значения и направления
вектора напряженности в каждой точке
электростатического поля, создаваемого системой
неподвижных зарядов Q1, Q2, , Qn.
• Опыт показывает, что к кулоновским силам применим
рассмотренный в механике принцип независимости
действия сил, т.е. результирующая сила, действующая со
стороны поля на пробный заряд Qo, равна векторной сумме
сил приложенных к нему со стороны каждого из зарядов Qi:
n
F Fi .
i 1
(1.7)
26.
• Согласно (1.4), F = Qo E и F = Qo E i ,i
• где E — напряженность результирующего поля,
• а E i — напряженность поля, создаваемого
зарядом Qi,. Подставляя последние выражения в
(1.7), получим
n
(1.8)
E Ei .
i 1
• Формула (1.8) выражает принцип суперпозиции
(наложения) электростатических полей:
напряженность результирующего поля,
создаваемого системой зарядов, равна
геометрической сумме напряженностей полей,
создаваемых в данной точке каждым из зарядов в
отдельности.
27.
• Электрический диполь — система двух равныхпо модулю разноименных точечных зарядов ( + Q,
— Q), расстояние между которыми значительно
меньше расстояния до рассматриваемых точек
поля. Вектор, направленный по оси диполя
(прямой, проходящей через оба заряда) от
отрицательного заряда к положительному и
равный расстоянию между ними, называется
плечом диполя l. Вектор
p Ql ,
(1.9)
• совпадающий по направлению с плечом диполя и
равный произведению заряда на плечо ,
называется электрическим моментом диполя
или дипольным моментом (рис. 6).
28.
QQ
р
l
-
+
Рисунок 6
• Согласно принципу суперпозиции (1.8),
напряженность поля диполя в произвольной точке
Е Е Е ,
29.
• Воспользовавшись этой формулой, рассчитаемнапряженность поля на продолжении оси диполя и
на перпендикуляре к середине его оси.
ЕВ
l
0
Е-
+
А
Е-
r
ЕА
Е+
Рисунок 7
r'
Е+
В
30.
Напряженность поля на продолжении оси
диполя в точке А (рис. 7).
Е А Е Е .
Обозначив расстояние от точки А до середины
оси диполя через , на основании формулы (1.5)
для вакуума можно записать
Q Q (r l / 2) 2 (r l / 2)2
1 Q
EA
.
2
2
2
2
4 0 (r l / 2) (r l / 2) 4 0 (r l / 2) (r l / 2)
Согласно определению диполя, l /2 r, поэтому
1 2Ql
1 2p
EA
.
3
3
4 0 r
4 0 r
31.
Напряженность поля на перпендикуляре,восставленном к оси из его середины, в точке В
(рис. 7).
• Точка В равноудалена от зарядов, поэтому
1
Q
1 Q
E E
,
4 0 (r ) 2 l 2 / 4 4 0 (r ) 2
(1.10)
• где r — расстояние от точки В до середины плеча
диполя.
• Из подобия равнобедренных треугольников,
опирающихся на плечо диполя и вектор , получим
EB
E
l
l
,
2
2
(r ) (l / 2) r
32.
• Откуда(1.11)
l
EB E .
r
• Подставив в выражение (1.11) значение (1.10),
получим
1
Ql
1
p
EB
.
3
3
4 0 (r ) 4 0 (r )
• Вектор имеет направление, противоположное
электрическому моменту диполя (вектор
направлен от отрицательного заряда к
положительному).
33.
Теорема ГауссаЦиркуляция вектора
напряженности
электростатического поля
Лекция 3
34.
Теорема Гаусса для электростатическогополя в вакууме
• Вычисление напряженности поля системы
электрических зарядов с помощью принципа
суперпозиции электростатических полей можно
значительно упростить, используя выведенную
немецким ученым К.Гауссом теорему,
определяющую поток вектора напряженности
электрического поля через произвольную
замкнутую поверхность.
35.
• В соответствии с формулой (1.6) поток векторанапряженности сквозь сферическую поверхность
радиуса r, охватывающую точечный заряд Q,
находящийся в ее центре (рис. 8),
ФE En dS
S
Q
4 0 r
2
Q
2
4 r .
0
E
Q
+
r
+
Рисунок 8
Q
Рисунок 9
36.
• Если замкнутая поверхность не охватываетзаряда, то поток сквозь нее равен нулю, так как
число линий напряженности, входящих в
поверхность, равно числу линий напряженности,
выходящих из нее.
• Таким образом, для поверхности любой формы,
если она замкнута и заключает
в себя точечный
заряд Q, поток вектора Е будет равен Q / 0 , т. е.
Q
ФE E dS En dS .
S
S
0
(1.12)
• Знак потока совпадает со знаком заряда Q.
37.
• Рассмотрим общий случай произвольнойповерхности, окружающей зарядов. В
соответствии с принципом суперпозиции (1.8)
напряженность поля, создаваемого всеми
зарядами, равна сумме напряженностей,
создаваемых каждым зарядом в отдельности.
Поэтому
ФE E dS Ei dS Ei dS .
i S
S
S i
• Согласно (1.12), каждый из интегралов, стоящий
под знаком суммы, равен Q / 0 . Следовательно,
38.
1 n
E dS En dS Qi .
S
S
0 i 1
(1.13)
• Формула (1.13) выражает теорему Гаусса для
электростатического поля в вакууме:
• поток вектора напряженности электростатического
поля в вакууме сквозь произвольную замкнутую
поверхность равен алгебраической сумме
заключенных внутри этой поверхности зарядов,
деленной на
.
0
• Эта теорема выведена математически для векторного поля
любой природы русским математиком М. В. Остроградским,
а затем независимо от него применительно к
электростатическому полю — К. Гауссом.
39.
• В общем случае электрические заряды могут быть«размазаны» с некоторой объемной плотностью
dQ
,
dV
• различной в разных местах пространства.
• Тогда суммарный заряд, заключенный внутри
замкнутой поверхности S, охватывающей
некоторый объем V,
Qi dV .
i
V
• И теорему Гаусса (1.13) можно записать так:
1
E dS En dS dV .
S
S
0 V
40.
• Дана система точечных зарядов в вакууме изамкнутые поверхности S1, S2 и S3. Поток вектора
напряженности электростатического поля равен
нулю через…
41.
• На рисунке изображены тонкая равномерно заряженнаянить длиной 1 м и равномерно заряженный цилиндр
радиусом 1 см и длиной 1 м. Величины зарядов нити и
цилиндра одинаковы.
• Как соотносятся между собой напряженность
электрического поля, созданного нитью в точке А,
справа от нити и напряженность поля, созданного
цилиндром в точке А справа от цилиндра?
42.
Применение теоремы Гаусса к расчетунекоторых электростатических полей в
вакууме
• 1. Поле равномерно заряженной бесконечной
плоскости. Бесконечная плоскость (рис.10)
заряжена с постоянной поверхностной
плотностью +σ (σ = dQ
–
заряд,
приходящийся
dS
на единицу поверхности).
• В качестве замкнутой поверхности мысленно
построим цилиндр, основания которого
параллельны заряженной плоскости, а ось
перпендикулярна ей.
43.
Рисунок 10• Так как образующие цилиндра параллельны линиям
напряженности (cos = 0), то поток вектора напряженности
сквозь боковую поверхность цилиндра равен нулю, а
полный поток сквозь цилиндр равен сумме потоков сквозь
его основания, т.е. равен 2ES.
44.
• Заряд, заключенный внутри построеннойцилиндрической поверхности, равен S. Согласно
теореме Гаусса (1.13), 2ES = S/ 0 , откуда
Е /(2 0 ) .
(1.14)
• Из формулы (1.14) вытекает, что напряженность
поля Е на любых расстояниях от заряженной
плоскости одинакова по модулю, иными словами,
поле равномерно заряженной плоскости
однородно.
• 2. Поле двух бесконечных параллельных
разноименно заряженных плоскостей (рис. 11).
Пусть плоскости заряжены равномерно
разноименными зарядами с поверхностными
плотностями +σ и -σ .
45.
• Поле таких плоскостей найдем как суперпозициюполей, создаваемых каждой из плоскостей в
отдельности.
+σ
-σ
• Слева и справа от плоскостей
• поля вычитаются (линии
• напряженности направлены
• навстречу друг другу),
• поэтому здесь напряженность
• поля Е = 0. В области между
Рисунок 11
• плоскостями ( определяются
• по формуле (1.14)), поэтому
• результирующая напряженность
Е / 0 .
(1.15)
46.
• 3. Поле равномерно заряженной сферическойповерхности.
• Сферическая поверхность радиуса R с общим
зарядом Q заряжена равномерно с
поверхностной плотностью +σ.
+
+
σ
+
+
+
R r
r'
+
+
+
+
+
+
+
Рисунок 12
47.
• Построим мысленно сферу радиуса r, имеющуюобщий центр с заряженной сферой. Если r > R, то
внутрь поверхности попадает весь заряд Q,
создающий рассматриваемое поле, и, по теореме
Гаусса (1.13),
2
4 r E Q / 0
• Откуда
1 Q
E
(
r
R
)
.
2
4 0 r
(1.16)
• При r > R поле убывает с расстоянием r по такому
же закону, как у точечного заряда.
• График зависимости Е от r приведен на рисунок
13.
48.
Е~
0
r=R
r
Рисунок 13
• Если r' < R, то замкнутая поверхность не содержит
внутри зарядов, поэтому внутри равномерно
заряженной сферической поверхности
электростатическое поле отсутствует (Е = 0).
49.
• 4. Поле объемно заряженного шара.• Шар радиуса R с общим зарядом Q заряжен
равномерно с объемной плотностью
( = dQ
– заряд, приходящийся на единицу
dV
• объема).
• Учитывая соображения симметрии (см. п. 3),
можно показать, что для напряженности поля вне
шара получится тот же результат, что и в
предыдущем случае (см. (1.16)).
• Внутри же шара напряженность поля будет другая.
• Сфера радиуса r' < R охватывает заряд
Q 4 3 r 3
50.
• Поэтому, согласно теореме Гаусса (1.13),2
3
4
4 r E Q / 0 3 r / 0
3
4
Q /( 3 R )
• Учитывая, что
• Получим
1
Q
E
r
(
r
R
)
.
3
4 0 R
(1.17)
• Таким образом, напряженность поля вне
равномерно заряженного шара описывается
формулой (1.16), а внутри его изменяется линейно
с расстоянием
согласно выражению (1.17).
r
51.
• График зависимости Е от r приведен на рисунке14.
Е
~
1
2
r
~r
0
ρ >0
r=R
Рисунок 14
r
52.
• 5. Поле равномерно заряженного бесконечногоцилиндра (нити).
• Бесконечный цилиндр радиуса R (рис. 15) заряжен
равномерно с линейной плотностью
dQ
• (
– заряд, приходящийся на единицу длины).
dl
• Из соображений симметрии следует, что линии
напряженности будут направлены по радиусам
круговых сечений цилиндра с одинаковой густотой
во все стороны относительно оси цилиндра.
• В качестве замкнутой поверхности мысленно
построим коаксиальный с заряженным цилиндр
радиуса r и высотой l.
53.
Рисунок 1554.
• Поток вектора сквозь торцы коаксиальногоцилиндра равен нулю (торцы параллельны линиям
напряженности), а сквозь боковую поверхность —
2 rlE
• По теореме Гаусса (1.13), при r > R
l
2 rlE =
0
• откуда
1
E
(r R)
2 0 r
,
(1.18)
55.
Циркуляция вектора напряженностиэлектростатического поля
F
α
dr
dl
+
1
Q0
r
r1
r2
+
Q
Рисунок 16
2
56.
• Если в электростатическом поле точечного зарядаQ из точки 1 в точку 2 вдоль произвольной
траектории (рис. 16) перемещается другой
точечный заряд Qo, то сила, приложенная к заряду,
совершает работу.
• Работа силы F на элементарном перемещении dl
равна
1 QQo
dA Fdl Fdl cos
dl cos .
2
4 0 r
• Так как dl cosα = dr , то
1 QQo
dA
dr
.
2
4 0 r
57.
• Работа при перемещении заряда Qo из точки 1 вточку 2
QQo r dr
1 QQo QQo
A12 dA
2
4 0 r 4 0 r1
r2
r2
r1
2
(1.19)
r1
• не зависит от траектории перемещения, а
определяется только положениями начальной 1 и
конечной 2 точек.
• Следовательно, электростатическое поле
точечного заряда является потенциальным, а
электростатические силы — консервативными.
58.
• Из формулы (1.19) следует, что работа,совершаемая при перемещении электрического
заряда во внешнем электростатическом поле по
любому замкнутому пути L, равна нулю, т. е
dA 0 .
(1.20)
L
• Если в качестве заряда, переносимого в
электростатическом поле, взять единичный
точечный положительный заряд, то элементарная
работа сил поля на пути dl равна
Edl El dl
• Тогда формулу (1.20) можно записать в виде
59.
Edl El dl 0 .
L
(1.21)
L
• Интегралы в выражении (1.21) называются
циркуляцией вектора напряженности.
• Следовательно, циркуляция вектора
напряженности электростатического поля вдоль
любого замкнутого контура равна нулю.
• Силовое поле, обладающее свойством (1.21),
называется потенциальным.
• Из обращения в нуль циркуляции вектора следует, что
линии напряженности электростатического поля не
могут быть замкнутыми, они начинаются и кончаются
на зарядах или же уходят в бесконечность.
60.
Потенциалэлектростатического поля
Вычисление разности
потенциалов по
напряженности поля
Лекция 4
61.
Потенциал электростатического поля• Тело, находящееся в потенциальном поле сил (в
электростатическом поле), обладает
потенциальной энергией, за счет которой силами
поля совершается работа.
• Как известно, работа консервативных сил
(кулоновских сил) совершается за счет убыли
потенциальной энергии.
• Поэтому работу сил электростатического поля
можно представить как разность потенциальных
энергий, которыми обладает точечный заряд Qo в
начальной и конечной точках поля заряда Q:
62.
1 QQo QQoA12 dA
U1 U 2 ,
r1
r2
4
0
r
r2
(2.1)
1
• откуда следует, что потенциальная энергия заряда
Qo в поле заряда Q равна
1 QQo
U
C.
4 0 r
• Она, как и в случае гравитационного поля,
определяется не однозначно, а с точностью до
произвольной постоянной С.
63.
• Если считать, что при удалении заряда вбесконечность ( r ) его потенциальная энергия
обращается в нуль (U = 0), то С = 0 и
потенциальная энергия заряда Qo, находящегося в
поле заряда Q на расстоянии r от него, равна
1 QQo
U
.
4 0 r
(2.2)
• Для одноименных зарядов QoQ > 0 и
потенциальная энергия их взаимодействия
(отталкивания) положительна, для разноименных
зарядов QoQ < 0 и потенциальная энергия их
взаимодействия (притяжения) отрицательна.
64.
• Если поле создается системой n точечных зарядовQ1, Q2, ..., Qn, то работа электростатических сил,
совершаемая над зарядом Qo, равна
алгебраической сумме работ сил, обусловленных
каждым из зарядов в отдельности.
• Поэтому потенциальная энергия U заряда Qo,
находящегося в этом поле, равна сумме его
потенциальных энергий U i , создаваемых каждым
из зарядов в отдельности:
n
n
U U i Qo
i 1
Qi
4
r
0
i
i 1
.
(2.3)
65.
• Из формул (2.2) и (2.3) вытекает, что отношениеU/Qo не зависит от Qo, поэтому оно является
энергетической характеристикой
электростатического поля, называемой
потенциалом:
U / Qo .
(2.4)
• Потенциал φ в какой-либо точке
электростатического поля есть физическая
величина, определяемая потенциальной энергией
единичного положительного заряда, помещенного
в эту точку.
66.
• Из формул (2.4) и (2.2) следует, что потенциалполя, создаваемого точечным зарядом Q, равен
1 Q
.
4 0 r
(2.5)
• Работа, совершаемая силами электростатического
поля при перемещении заряда Qo из точки 1 в
точку 2 (см. (2.1), (2.4), (2.5)), может быть
представлена как
A12 U 1 U 2 Qo ( 1 2 ) ,
(2.6)
• т. е. равна произведению перемещаемого заряда
на разность потенциалов в начальной и конечной
точках.
67.
• Разность потенциалов двух точек 1 и 2 вэлектростатическом поле определяется работой,
совершаемой силами поля, при перемещении
единичного положительного заряда из точки 1 в
точку 2.
• Работа сил поля при перемещении заряда Qo из
точки 1 в точку 2 может быть записана также в
2
виде
A12 Qo E dl .
(2.7)
1
• Приравняв (2.6) и (2.7), придем к выражению для
разности потенциалов:
2
1 2 E dl El dl ,
2
1
1
(2.8)
68.
• Если перемещать заряд Qo из произвольной точкив бесконечность, где по условию потенциал равен
нулю, то работа сил электростатического поля,
согласно (2.6),
A Q
откуда
o
A / Qo .
(2.9)
Таким образом, потенциал — физическая величина,
определяемая работой по перемещению
единичного положительного заряда при удалении
его из данной точки в бесконечность.
69.
• Из выражения (2.4) следует, что единицапотенциала — вольт (В): 1 В есть потенциал такой
точки поля, в которой заряд в 1 Кл обладает
потенциальной энергией 1 Дж (1 В = 1 Дж/Кл).
• Из формул (2.3) и (2.4) вытекает, что если поле
создается несколькими зарядами, то потенциал
поля системы зарядов равен алгебраической
сумме потенциалов полей всех этих зарядов:
n
i
i 1
1
n Q
i
4 0 i 1 ri
.
70.
Напряженность как градиент потенциала.Эквипотенциальные поверхности
• Найдем взаимосвязь между напряженностью
электростатического поля, являющейся его
силовой характеристикой, и потенциалом —
энергетической характеристикой поля.
• Работа по перемещению единичного точечного
положительного заряда из одной точки в другую
вдоль оси х при условии, что точки расположены
бесконечно близко друг к другу равна E x dx
.
• Та же работа равна 1 2 d .
• Приравняв оба выражения, можем записать
71.
Ex
,
x
(2.10)
где символ частной производной подчеркивает, что
дифференцирование производится только по х.
Повторив аналогичные рассуждения
для осей у и z,
можем найти вектор E :
E i
j k ,
y
z
x
Из определения градиента следует, что
E grad
или
E
(2.11)
72.
• Для графического изображения распределенияпотенциала электростатического поля пользуются
эквипотенциальными поверхностями —
поверхностями, во всех точках которых потенциал
имеет одно и то же значение.
• Если поле создается точечным зарядом, то его
потенциал, согласно (2.5),
1
Q
4 0 r
• Таким образом, эквипотенциальные поверхности в
данном случае — концентрические сферы.
73.
• Линии напряженности всегда нормальны кэквипотенциальным поверхностям.
• Эквипотенциальных поверхностей вокруг каждого
заряда и каждой системы зарядов можно провести
бесчисленное множество. Однако их обычно
проводят так, чтобы разности потенциалов между
любыми двумя соседними эквипотенциальными
поверхностями были одинаковы.
• Тогда густота эквипотенциальных поверхностей
наглядно характеризует напряженность поля в
разных точках. Там, где эти поверхности
расположены гуще, напряженность поля больше.
74.
+б)
а)
Рисунок 17
75.
76.
77.
• На рисунке показаны эквипотенциальныеповерхности электростатического поля.
• Вектор напряженности поля имеет
направление…
78.
• В вершинах равностороннего треугольниканаходятся заряды, одинаковые по модулю.
• Сила, действующая на верхний заряд, и
напряженность поля в месте нахождения
этого заряда обозначены векторами ….
79.
• Поле создано бесконечной равномернозаряженной плоскостью.
• Укажите направление вектора градиента
потенциала в точке А.
80.
Вычисление разности потенциалов понапряженности поля
• 1. Поле равномерно заряженной бесконечной
плоскости определяется формулой (1.14):
Е /( 2 0 )
• где σ — поверхностная плотность заряда.
Разность потенциалов между точками, лежащими
на расстояниях х1 и х2 от плоскости (см. формулу
(2.10)), равна
1 2 E dx
dx
( x2 x1 ) .
2
2
0
0
x
х2
x2
х1
1
81.
• 2. Поле двух бесконечных параллельныхразноименно заряженных плоскостей
определяется формулой (1.15):
E / 0
• Разность потенциалов между плоскостями,
расстояние между которыми равно d (см. формулу
(2.1)), равна
1 2 E dx dx d .
0
0
0
d
0
d
(2.12)
82.
• 3. Поле равномерно заряженной сферическойповерхности радиуса R с общим зарядом Q вне
сферы (r > R) вычисляется по (1.16):
1
Q
E
2
4 0 r
• Разность потенциалов между двумя точками,
лежащими на расстояниях r1 и r2 от центра сферы
( r1 > R, r2 > R), равна
Q
Q 1
1
1 2 E dr
dr
. (2.13)
2
4
4
r
r
r
0
0
1
2
r
r2
r2
r1
1
1
83.
• Если принять 1 = r и 2 =, то потенциал поля
вне сферической поверхности, согласно формуле
(86.2), задается выражением
r
r
1 Q
4 0 r
• Внутри сферической поверхности потенциал всюду
одинаков и равен
1 Q
.
4 0 R
• График зависимости φ от r приведен на рисунке 18.
84.
φ1
~ r
r=R
Рис. 18
r
85.
• 4. Поле объемно заряженного шара радиуса R собщим зарядом Q вне шара (r > R) вычисляется по
формуле (82.3), поэтому разность потенциалов
между двумя точками, лежащими вне шара
определяется формулой (86.2).
• В любой точке, лежащей внутри шара на
расстоянии, напряженность определяется
выражением (82.4):
1 Q
Е=
4 0 R
r
3
• Следовательно, разность потенциалов между
двумя точками, лежащими внутри шара
r2
1 2 E dr
r1
Q
8 0 R
2 2 r1 2 ) .
(
r
3
86.
• 5. Поле равномерно заряженного бесконечногоцилиндра радиуса R, заряженного с линейной
плотностью , вне цилиндра (r > R) определяется
формулой (1.18):
1
E
2 0 r
• Следовательно, разность потенциалов между
двумя точками, лежащими вне цилиндра, равна
dr
r2
1 2 E dr
ln .
2 0 r r 2 0 r1
r2
r1
r2
1
(2.14)
87.
Типы диэлектриков.Поляризация диэлектриков
• Положительный заряд всех ядер молекулы равен
суммарному заряду электронов, т.е. молекула в
целом электрически нейтральна.
• Если заменить положительные заряды ядер
молекул суммарным зарядом +Q, находящемся в
центре «тяжести» положительных зарядов, а заряд
всех электронов — суммарным отрицательным
зарядом -Q, находящемся в центре «тяжести»
отрицательных зарядов, то молекулу можно
рассматривать как электрический диполь с
электрическим моментом, определенным
формулой (1.9).
88.
p Ql ,• Первую группу диэлектриков (N2, Н2, О2, СО2, ...)
составляют вещества, молекулы которых имеют
симметричное строение, т. е. центры «тяжести»
положительных и отрицательных зарядов в
отсутствие внешнего электрического поля
совпадают, т.е. дипольный момент молекулы
равен нулю.
• Молекулы таких диэлектриков называются
неполярными. Под действием внешнего
электрического поля заряды неполярных молекул
смещаются в противоположные стороны и
молекула приобретает дипольный момент.
89.
Вторую группу диэлектриков (Н2О, NН3, SO2, СО, ...)составляют вещества, молекулы которых имеют
асимметричное строение, т. е. центры «тяжести»
положительных и отрицательных зарядов не
совпадают. Эти молекулы в отсутствие внешнего
электрического поля обладают дипольным
моментом.
Молекулы таких диэлектриков называются
полярными. При отсутствии внешнего поля
дипольные моменты полярных молекул
вследствие теплового движения ориентированы в
пространстве хаотично и их результирующий
момент равен нулю.
Если такой диэлектрик поместить во внешнее поле,
то диполи будут ориентироваться вдоль поля и
возникнет отличный от нуля результирующий
момент.
90.
• Третью группу диэлектриков (NaCl, КСl, КВг,...)составляют вещества, молекулы которых имеют
ионное строение.
• Ионные кристаллы представляют собой
пространственные решетки с правильным
чередованием ионов разных знаков. В этих
кристаллах нельзя выделить отдельные молекулы,
а рассматривать их можно как систему двух
вдвинутых одна в другую ионных подрешеток.
• При наложении на ионный кристалл
электрического поля происходит некоторая
деформация кристаллической решетки или
относительное смещение подрешеток,
приводящее к возникновению дипольных
моментов.
91.
• Таким образом, внесение всех трех группдиэлектриков во внешнее электрическое поле
приводит к возникновению отличного от нуля
результирующего электрического момента
диэлектрика, или, иными словами, к поляризации
диэлектрика.
• Поляризацией диэлектрика называется процесс
ориентации диполей или появления под
воздействием электрического поля
ориентированных по полю диполей.
• Соответственно трем группам диэлектриков
различают три вида поляризации:
92.
• электронная, или деформационная,поляризация диэлектрика с неполярными
молекулами, заключающаяся в возникновении у
атомов индуцированного дипольного момента за
счет деформации электронных орбит;
• ориентационная, или дипольная, поляризация
диэлектрика с полярными молекулами,
заключающаяся в ориентации имеющихся
дипольных моментов молекул по полю.
Естественно, что тепловое движение препятствует
полной ориентации молекул. Эта ориентация тем
сильнее, чем больше напряженность
электрического поля и ниже температура;
• ионная поляризация диэлектриков с ионными
кристаллическими решетками, заключающаяся в
смещении подрешетки положительных ионов
вдоль поля, а отрицательных — против поля,
приводящем к возникновению дипольных
моментов.
93.
Электростатическое поле вдиэлектрике
Лекция 5
94.
Поляризованность.Напряженность поля в диэлектрике
• При помещении диэлектрика во внешнее
электростатическое поле он поляризуется, т. е.
приобретает отличный от нуля дипольный момент
pV pi
pi
i
— дипольный момент одной молекулы.
95.
• Для количественного описания поляризациидиэлектрика пользуются векторной величиной —
поляризованностью, определяемой как
дипольный момент единицы объема диэлектрика:
P pV /V pi / V .
(2.15)
i
• Из опыта следует, что для большого класса
диэлектриков (за исключением сегнетоэлектриков)
поляризованность линейно зависит от
напряженности
поля. Если диэлектрик изотропный
и E не слишком велико, то
P 0 E ,
(2.16)
96.
— диэлектрическая восприимчивость
вещества, безразмерная величина,
характеризующая свойства диэлектрика; она
всегда больше нуля.
• Для большинства диэлектриков (твердых и жидких)
она составляет несколько единиц (хотя, например,
для спирта 25, для воды 80).
• Для установления количественных
закономерностей поля в диэлектрике внесем в
однородное внешнее электростатическое поле
(создается двумя бесконечными параллельными
разноименно заряженными плоскостями)
пластинку из однородного диэлектрика,
расположив ее так, как показано на рисунке 19.
97.
• Под действием поля диэлектрик поляризуется, т. е.происходит смещение зарядов
+σ -σ'
+σ' -σ
Рисунок 19
98.
• Не скомпенсированные заряды + и - ,появляющиеся в результате поляризации
диэлектрика, называются связанными.
• Так как поверхностная плотность связанных
зарядов меньше плотности свободных зарядов
плоскостей, то не всё поле, создаваемое
плоскостями компенсируется полем зарядов
диэлектрика: часть линий напряженности пройдет
сквозь диэлектрик, другая же часть — обрывается
на связанных зарядах (см. рис. 19).
• Результирующее поле внутри диэлектрика
Е Ео Е .
• Е - поле, создаваемое свободными зарядами
о
99.
Е / 0Е - поле, создаваемое связанными зарядами.
• Т.е.
Е Ео / 0 .
(2.17)
• Определим поверхностную плотность связанных
зарядов. По (2.15), полный дипольный момент
рV = PV = PSd,
пластинки диэлектрика
• где S — площадь грани пластинки, d — ее
толщина.
100.
• С другой стороны, полный дипольный момент,согласно (80.3), равен произведению связанного
заряда каждой грани Q S на расстояние d
между ними, т.е.
pV Sd
• Таким образом
• или
PSd Sd
P,
(2.18)
• т. е. поверхностная плотность связанных зарядов
равна поляризованности Р.
101.
• Подставив в (2.17) выражения (2.18) и (2.16),получим
Е Ео Е
• откуда напряженность результирующего поля
внутри диэлектрика равна
Е Ео /(1 ) Ео / .
(2.19)
• Безразмерная величина
1
(2.20)
• называется диэлектрической проницаемостью
среды. Она показывает, во сколько раз поле
ослабляется диэлектриком.
102.
Электрическое смещение.Теорема Гаусса для электростатического
поля в диэлектрике
• Напряженность электростатического поля,
согласно (2.19), зависит от свойств среды: в
однородной изотропной среде напряженность поля
Е обратно пропорциональна ε.
• Вектор Е , на границе диэлектриков, претерпевает
скачкообразное изменение, создавая тем самым
неудобства при расчете электростатических полей.
Поэтому удобно помимо вектора напряженности
характеризовать поле еще вектором
электрического смещения, который для
электрически изотропной среды по определению
равен:
103.
D 0 E .(2.21)
• Используя формулы (2.20) и (2.16), вектор
электрического смещения можно выразить как
D 0 E P.
(2.22)
• Единица измерения электрического смещения —
кулон на метр в квадрате (Кл/м2).
• В диэлектрике на электростатическое поле
свободных зарядов накладывается
дополнительное поле связанных зарядов.
• Результирующее поле в диэлектрике описывается
вектором напряженности Е , который зависит от
свойств диэлектрика.
104.
• Вектором D описывает электростатическое поле,создаваемое свободными зарядами. Связанные
заряды, возникающие в диэлектрике, могут
вызвать, перераспределение свободных зарядов,
создающих поле.
• Поэтому вектор электрического смещения D
характеризует электростатическое поле,
создаваемое свободными зарядами (т. е. в
вакууме), но при таком их распределении в
пространстве, какое имеется при наличии
диэлектрика.
• Поле D изображается с помощью линий
электрического смещения, направление и
густота которых определяются
точно так же, как и
для линий напряженности Е .
105.
• Линии вектора Е могут начинаться изаканчиваться на любых зарядах — свободных
и
связанных, в то время как линии вектора D —
только на свободных зарядах.
• Через области поля, где находятся связанные
заряды, линии вектора D проходят не прерываясь.
• Для произвольной
замкнутой поверхности S поток
вектора D сквозь эту поверхность
ФD D dS Dn dS .
S
S
106.
Теорема Гаусса для электростатического поля вдиэлектрике:
n
D dS Dn dS Qi ,
i 1
S
S
(2.23)
Dn 0 En ( 1)
• Для вакуума
n
• Поэтому
0 En dS Qi .
S
i 1
• Так как источниками поля Е в среде являются как
свободные, так и связанные заряды, то теорему
Гаусса в самом общем виде можно записать:
107.
nn
0 Е dS 0 Еn dS Qi Qiсс ,
S
S
n
i 1
i 1
Qiсс — соответственно
• где , Qi и
i 1
i 1
алгебраические суммы свободных и связанных
зарядов, охватываемых замкнутой поверхностью
S.
• Однако эта формула неприемлема для описания
поля Е в диэлектрике, так как
она выражает
свойства неизвестного поля Е через связанные
заряды, которые, в свою очередь, определяются
им же. Это еще раз доказывает целесообразность
введения вектора электрического смещения.
n
108.
Условия на границе раздела двухдиэлектрических сред
• Рассмотрим связь между векторами Е и D на
границе раздела двух однородных изотропных
диэлектриков (диэлектрические проницаемости
которых 1 и 2 ) при отсутствии на границе
свободных зарядов.
• Построим вблизи границы раздела диэлектриков
1 и 2 небольшой замкнутый прямоугольный контур
ABCDA длины l, ориентировав его так, как
показано на рисунок 20.
109.
Рисунок 20110.
• Согласно теореме (1.21) о циркуляции вектора Е ,E dl 0 ,
ABCDA
• Откуда
E2 l E1 l 0
• (знаки интегралов по АВ и CD разные, так как пути
интегрирования противоположны, а интегралы по
участкам ВС и DA ничтожно малы). Поэтому
Е1 Е2 .
(2.24)
• Заменив, согласно (2.21),
проекции вектора Е
проекциями вектора D , получим
111.
D1 1
.
D2 2
(2.25)
• На границе раздела двух диэлектриков (рис. 21)
построим прямой цилиндр ничтожной высоты, одно
основание которого находится в первом
диэлектрике, другое — во втором.
• Основания S настолько малы, что в пределах
каждого из них вектор D одинаков.
112.
Рисунок 21113.
• Согласно теореме Гаусса (2.23),D2n S D1n S 0
• (нормали и к основаниям цилиндра направлены
противоположно).
• Поэтому
D1n D2n .
(2.26)
• Заменив, согласно (2.21),
проекции вектора D
проекциями вектора Е , получим
Е1n 2
.
E2n 1
(2.27)
114.
• Таким образом, при переходе через границураздела двух диэлектрических сред
тангенциальная составляющая вектора
Е ( E ) и
нормальная составляющая вектора D ( D n )
изменяются непрерывно (не претерпевают
скачка),
а нормальная составляющая вектора Е ( E n ) и
тангенциальная составляющая вектора D ( D )
претерпевают скачок.
• Из условий (2.24) — (2.27) для составляющих
векторов Е и D следует, что линии этих
векторов испытывают излом (преломляются).
115.
Рисунок 22116.
Из рисунка 22 следует ( 2 ),что
1
tg 2 E2 / E2n
.
tg 1 E1 / E1n
Учитывая записанные выше условия, получим закон
преломления линий напряженности (а значит, и
линий смещения)
tg 2 2
.
tg 1 1
Эта формула показывает, что, входя в диэлектрик с
большей диэлектрической проницаемостью, эти
линии удаляются от нормали.
117.
Сегнетоэлектрики• Сегнетоэлектрики — диэлектрики, обладающие в
определенном интервале температур спонтанной
(самопроизвольной) поляризованностью в
отсутствие внешнего электрического поля.
• К сегнетоэлектрикам относятся, например,
сегнетова соль NaKC4H4O6 4H2O (от нее и
получили свое название сегнетоэлектрики) и
титанат бария ВаТiО3.
• При отсутствии внешнего электрического поля
сегнетоэлектрик представляет собой мозаику из
доменов — областей с различными
направлениями поляризованности.
118.
Рисунок 23119.
• Так как в смежных доменахнаправления вектора
поляризованности Р различны, то в целом
дипольный момент диэлектрика равен нулю.
• При внесении сегнетоэлектрика во внешнее поле
происходит переориентация дипольных моментов
доменов по полю.
• Поэтому сегнетоэлектрики имеют аномально
большие значения диэлектрической
проницаемости (для сегнетовой соли,
• например, max 104).
120.
• Сегнетоэлектрические свойства сильно зависят оттемпературы.
• Для каждого сегнетоэлектрика имеется
определенная температура, выше которой его
необычные свойства исчезают и он становится
обычным диэлектриком.
• Эта температура называется точкой Кюри (в
честь французского физика Пьера Кюри).
• В сегнетоэлектриках вблизи точки Кюри
наблюдается резкое возрастание теплоемкости
вещества.
• Превращение сегнетоэлектриков в обычный
диэлектрик, происходящее в точке Кюри,
сопровождается фазовым переходом II рода.
121.
• Диэлектрическая проницаемость(а
следовательно, и диэлектрическая
восприимчивость ) сегнетоэлектриков зависит
от напряженности Е поля в веществе, а для других
диэлектриков эти величины являются
характеристиками вещества.
• Для сегнетоэлектриков формула (2.16) не
соблюдается; для них связь между векторами
поляризованности ( Р ) и напряженности
( Е)
нелинейная и зависит от значений Е в
предшествующие моменты времени.
• В сегнетоэлектриках наблюдается явление
диэлектрического гистерезиса («запаздывания»)
(см. рис. 24).
122.
р2
р0
1
3
-ЕС
Е
Рисунок 24
123.
• Следует упомянуть еще о пьезоэлектриках —кристаллических веществах, в которых при сжатии или
растяжении в определенных направлениях возникает
электрическая поляризация даже в отсутствие внешнего
электрического поля (прямой пьезоэффект). Следствием
прямого пьезоэффекта является обратный пьезоэффект
— появление механической деформации под действием
электрического поля.
• У некоторых пьезоэлектриков решетка положительных
ионов в состоянии термодинамического равновесия
смещена относительно решетки отрицательных ионов, в
результате чего они оказываются электрически
поляризованными даже без внешнего электрического поля.
Такие кристаллы называются пироэлектриками.
• Еще существуют электреты — диэлектрики, длительно
сохраняющие поляризованное состояние после снятия
внешнего электрического поля (электрические аналоги
постоянных магнитов).
124.
Проводники вэлектростатическом поле
Электроёмкость
Лекция 6
125.
Проводники в электростатическом поле• Если поместить проводник во внешнее
электростатическое поле или его зарядить, то на
заряды проводника будет действовать
электростатическое поле, в результате чего они
начнут перемещаться.
• Перемещение зарядов (ток) продолжается до тех
пор, пока не установится равновесное
распределение зарядов, при котором
электростатическое поле внутри проводника
обращается в нуль.
• Это происходит в течение очень короткого
времени.
126.
• Отсутствие поля внутри проводника означает,согласно (2.11), что потенциал во всех точках
внутри проводника постоянен (φ = const), т. е.
поверхность проводника в электростатическом
поле является эквипотенциальной.
• Отсюда же следует, что вектор напряженности
поля на внешней поверхности проводника
направлен по нормали к каждой точке его
поверхности.
• Если бы это было не так, то под действием
касательной составляющей заряды начали бы по
поверхности проводника перемещаться, что, в
свою очередь, противоречило бы равновесному
распределению зарядов.
127.
• Если проводнику сообщить некоторый заряд Q, тонекомпенсированные заряды располагаются
только на поверхности проводника.
• Это следует непосредственно из теоремы Гаусса
(2.23), согласно которой заряд Q, находящийся
внутри проводника в некотором объеме,
ограниченном произвольной замкнутой
поверхностью, равен
Q D dS Dn dS 0 ,
S
S
• так как во всех точках внутри поверхности D = 0.
128.
• Найдем взаимосвязь между напряженностью Еполя вблизи поверхности заряженного проводника
и поверхностной плотностью σ зарядов на его
поверхности. Для этого применим теорему Гаусса
к бесконечно малому цилиндру с основаниями ΔS,
пересекающему границу проводник — диэлектрик.
Е
∆S
E1=0
Рисунок 25
129.
• Ось цилиндра ориентирована вдоль вектора Е(рис. 25).
• Поток вектора электрического смещения через
внутреннюю часть цилиндрической поверхности
равен нулю, так как внутри проводника Е 1 (а
следовательно,
и D1 ) равен нулю, поэтому поток
вектора D сквозь замкнутую цилиндрическую
поверхность определяется только потоком сквозь
наружное основание цилиндра.
• Согласно теореме Гаусса (2.23), этот поток (DΔS)
равен сумме зарядов (Q = σΔS), охватываемых
поверхностью: DΔS = σΔS, т.е.
D
• или
(3.1)
130.
E /( 0 ) ,
(3.2)
• Таким образом, напряженность
электростатического поля у поверхности
проводника определяется поверхностной
плотностью зарядов. Можно показать, что
соотношение (3.2) задает напряженность
электростатического поля вблизи поверхности
проводника любой формы.
• Если в электростатическое поле внести
нейтральный проводник, то свободные заряды
(электроны, ионы) будут перемещаться (рис. 26, а).
На одном конце проводника будет скапливаться
избыток положительного заряда, на другом —
избыток отрицательного.
• Эти заряды называются индуцированными.
131.
Рисунок 26132.
• Таким образом, нейтральный проводник, внесенныйв электростатическое поле, разрывает линий
напряженности; они заканчиваются на
отрицательных индуцированных зарядах и вновь
начинаются на положительных.
• Индуцированные заряды распределяются на
внешней поверхности проводника.
• Явление перераспределения поверхностных
зарядов на проводнике во внешнем
электростатическом поле называется
электростатической индукцией.
• Из рисунка 26, б следует, что индуцированные
заряды появляются на проводнике вследствие
смещения их под действием поля, т. е. σ является
поверхностной плотностью смещенных зарядов.
133.
• Так как в состоянии равновесия внутри проводниказаряды отсутствуют, то создание внутри него
полости не повлияет на конфигурацию
расположения зарядов и тем самым на
электростатическое поле. Следовательно, внутри
полости поле будет отсутствовать. Если теперь
этот проводник с полостью заземлить, то
потенциал во всех точках полости будет нулевым,
т. е. полость полностью изолирована от влияния
внешних электростатических полей.
• На этом основана электростатическая защита —
экранирование тел, например измерительных
приборов, от влияния внешних электростатических
полей.
134.
• Свойство зарядов располагаться на внешнейповерхности проводника используется для
устройства электростатических генераторов,
предназначенных для накопления больших
зарядов и достижения разности потенциалов в
несколько миллионов вольт.
• Электростатический генератор состоит из
шарообразного полого проводника 1 (рис. 27),
укрепленного на изоляторах 2. Движущаяся замкнутая
лента 3 из прорезиненной ткани заряжается от
источника напряжения с помощью системы остриев 4,
соединенных с одним из полюсов источника, второй
полюс которого заземлен. Заземленная пластина 5
усиливает стекание зарядов с остриев на ленту. Другая
система остриев 6 снимает заряды с ленты и передает
их полому шару, и они переходят на его внешнюю
поверхность.
135.
Электростатический генератор Ван де Граафа1
6
2
3
5
4
20 кВ
Рисунок 27
136.
Электрическая емкость уединенногопроводника
• Рассмотрим уединенный проводник, т. е.
проводник, который удален от других проводников,
тел и зарядов.
• Его потенциал, согласно (2.5), прямо
пропорционален заряду проводника.
• Из опыта следует, что разные проводники, будучи
одинаково заряженными, принимают различные
потенциалы. Поэтому для уединенного проводника
можно записать
Q C .
137.
• ВеличинуC Q /
(3.3)
• называют электроемкостью (или просто
емкостью) уединенного проводника.
• Емкость уединенного проводника определяется
зарядом, сообщение которого проводнику
изменяет его потенциал на единицу.
• Емкость проводника зависит от его размеров и
формы, но не зависит от материала, агрегатного
состояния, формы и размеров полостей внутри
проводника.
• Это связано с тем, что избыточные заряды
распределяются на внешней поверхности
проводника.
138.
• Единица электроемкости — фарад (Ф):• 1Ф — емкость такого уединенного проводника,
потенциал которого изменяется на 1В при
сообщении ему заряда в 1 Кл.
• Согласно (2.5), потенциал уединенного шара
радиуса R, находящегося в однородной среде с
диэлектрической проницаемостью ε, равен
1
Q
.
4 0 R
• Используя формулу (93.1), получим, что емкость
шара
C 4 0 R .
(3.4)
139.
• Отсюда следует, что емкостью в 1Ф обладал быуединенный шар, находящийся в вакууме и
имеющий радиус R = С/(4 0 ) 9 106 км, что
примерно в 1400 раз больше радиуса Земли
(электроемкость Земли С 0,7 мФ).
Следовательно, фарад — очень большая
величина, поэтому на практике используются
дольные единицы — миллифарад (мФ),
микрофарад (мкФ), нанофарад (нФ), пикофарад
(пФ).
• Из формулы (3.4) вытекает также, что единица
электрической постоянной фарад на метр (Ф/м)
(см. (1.3)).
140.
Конденсаторы• Для того чтобы проводник обладал большой
емкостью, он должен иметь очень большие
размеры.
• На практике, однако, необходимы устройства,
обладающие способностью при малых размерах и
небольших относительно окружающих тел
потенциалах накапливать значительные по
величине заряды, иными словами, обладать
большой емкостью.
• Эти устройства получили название
конденсаторов.
141.
• Если к заряженному проводнику приближатьдругие тела, то на них возникают индуцированные
(на проводнике) или связанные (на диэлектрике)
заряды, причем ближайшими к наводящему заряду
Q будут заряды противоположного знака.
• Эти заряды, естественно, ослабляют поле,
создаваемое зарядом Q, т. е. понижают потенциал
проводника, что приводит (см. (3.3)) к повышению
его электроемкости.
• Поэтому конденсатор состоит из двух проводников
(обкладок), разделенных диэлектриком.
142.
• На емкость конденсатора не должны оказыватьвлияния окружающие тела, поэтому проводникам
придают такую форму, чтобы поле, создаваемое
накапливаемыми зарядами, было сосредоточено в
узком зазоре между обкладками конденсатора.
• Этому условию удовлетворяют:
• 1) две плоские пластины; 2) два коаксиальных
цилиндра; 3) две концентрические сферы.
• Поэтому в зависимости от формы обкладок
конденсаторы делятся на плоские,
цилиндрические и сферические.
143.
• Под емкостью конденсатора понимаетсяфизическая величина, равная отношению заряда
Q конденсатора к разности потенциалов ( 1 2 )
между его обкладками:
С Q /( 1 2 ) .
(3.5)
• При наличии диэлектрика между обкладками
разность потенциалов между ними, согласно
(86.1),
(3.6)
d
/(
)
,
1
2
0
• Тогда из формулы (3.5), заменяя Q = σS, с учетом
(3.6) получим выражение для емкости плоского
конденсатора.
144.
• Ёмкость плоского конденсатораC 0 S / d .
(3.7)
• Ёмкость цилиндрического конденсатора:
C 2 0 l / ln(r2 / r1 ) .
(3.8)
• Ёмкость сферического конденсатора:
r1r2
C 4 0
.
r2 r1
(3.9)
145.
• Конденсаторы характеризуются пробивнымнапряжением — разностью потенциалов между
обкладками конденсатора, при которой происходит
пробой — электрический разряд через слой
диэлектрика в конденсаторе.
• Пробивное напряжение зависит от формы
обкладок, свойств диэлектрика и его толщины.
• Для увеличения емкости и варьирования ее
возможных значений конденсаторы соединяют в
батареи, при этом используется их параллельное
и последовательное соединение.
146.
• 1. Параллельное соединение конденсаторов(рис. 28).
Cn
В
А
C2
C1
Рисунок 28
• У параллельно соединенных конденсаторов
разность потенциалов на обкладках конденсаторов
одинакова и равна
А
В
147.
• Если емкости отдельных конденсаторов равны:Q1 C1 ( A B ) ,
Q2 C2 ( A B ) ,
----------------------------
Qn Cn ( A B ) ,
• а заряд батареи конденсаторов
n
Q Qi (C1 C2 ... Cn )( A B ) .
i 1
• Полная емкость батареи
n
С Q /( А В ) С1 С2 ... Сn Сi ,
i 1
148.
• 2. Последовательное соединениеконденсаторов (рис. 29).
∆φ
∆φ1
∆φ2 ∆φ3
∆φn
C1
C2
Cn
C3
Рисунок 29
• У последовательно соединенных конденсаторов
заряды всех обкладок равны по модулю, а
разность потенциалов на зажимах батареи
149.
ni ,
i 1
• где для любого из рассматриваемых
конденсаторов
i Q / Ci .
• С другой стороны,
n
Q / C Q (1 / Ci ) ,
i 1
• откуда
n
1 / C (1 / Ci ) ,
i 1
150.
Энергия системы зарядов, уединенногопроводника и конденсатора.
Энергия электростатического поля
• 1. Энергия системы неподвижных точечных
зарядов.
• Электростатические силы взаимодействия
консервативны; следовательно, система зарядов
обладает потенциальной энергией.
• Найдем потенциальную энергию системы двух
неподвижных точечных зарядов.
• Каждый из этих зарядов в поле другого обладает
потенциальной энергией (см. (2.2) и (2.5)):
W1 Q1 12 ,
W2 Q2 21 ,
151.
• Согласно (2.5),1 Q2
12
4 0 r
• Поэтому
1 Q1
21
4 0 r
W1 W2 W
• и
W Q1 12 Q2 21 1 (Q1 12 Q2 21 ) .
2
152.
• Если у нас не два, а n зарядов, то1 n
W Qi i ,
2 i 1
(3.10)
• где i , — потенциал, создаваемый в той точке, где
находится заряд Qi всеми зарядами, кроме i-ro.
• 2. Энергия заряженного уединенного
проводника.
• Пусть имеется уединенный проводник, заряд,
емкость и потенциал которого соответственно
равны Q, С, φ.
• Увеличим заряд этого проводника на dQ.
153.
• Для этого необходимо перенести заряд dQ избесконечности на уединенный проводник, затратив
на это работу, равную
dA dQ C d .
• Чтобы зарядить тело от нулевого потенциала до ,
необходимо совершить работу
2
A C d C / 2 .
(3.11)
0
• Энергия заряженного проводника равна той
работе, которую необходимо совершить, чтобы
зарядить этот проводник:
• W C 2 / 2 Q / 2 Q 2 /(2C ) .
(3.12)
154.
• 3. Энергия заряженного конденсатора.• Как всякий заряженный проводник, конденсатор
обладает энергией, которая в соответствии с
формулой (95.3) равна
W C ( )2 / 2 Q / 2 Q 2 /(2C) ,
(3.13)
• Используя выражение (3.13), можно найти
механическую (пондеромоторную) силу, с которой
пластины конденсатора притягивают друг друга.
Для этого предположим, что расстояние х между
пластинами меняется, например, на величину dх.
Тогда действующая сила совершает работу
dA F dx
155.
• При этом изменяется потенциальная энергиясистемы
F dx dW ,
• Откуда
dW
F
.
dx
(3.14)
• Подставив в (95.4) выражение (94.3), получим
2
2
Q
Q
W
x.
2C 2 0 S
(3.15)
• Производя дифференцирование найдем искомую
2
силу
dW
Q
F
dx
2 0 S
,
156.
• 4. Энергия электростатического поля.• Преобразуем формулу (3.13), выражающую
энергию плоского конденсатора посредством
зарядов и потенциалов, воспользовавшись
выражениеми для емкости плоского конденсатора
(C = 0 S/d) и разности потенциалов между его
обкладками ( = Ed). Тогда получим
W
0 E
2
2
Sd
0 E
2
2
V,
• где V = Sd — объем конденсатора.
(3.16)
157.
• Объемная плотность энергииэлектростатического поля (энергия единицы
объема)
2
E
ED
0
(3.17)
w W /V
.
2
2
• Выражение (95.8) справедливо только для
изотропного диэлектрика, для которого
выполняется соотношение (88.2):
P 0 E
158.
Постоянный электрический токЗакон Ома
Сопротивление проводников
Лекция 7
159.
Постоянный электрический токЭлектрическим током называется любое
упорядоченное (направленное) движение
электрических зарядов.
В проводнике возникает электрический ток,
называемый током проводимости.
Если же упорядоченное движение электрических
зарядов осуществляется перемещением в
пространстве заряженного макроскопического тела
(рис. 146, б), то возникает так называемый
конвекционный ток.
160.
• а) – ток проводимости,• б) – конвекционный ток
Е
а)
-
б)
+
+
+
+
+
+
+
+
Рисунок 30
161.
• Для возникновения и существованияэлектрического тока необходимо, с одной
стороны, наличие свободных носителей
тока — заряженных частиц, способных
перемещаться упорядоченно, а с другой —
наличие электрического поля, энергия
которого, каким-то образом восполняясь,
расходовалась бы на их упорядоченное
движение.
• За направление тока условно принимают
направление движения положительных
зарядов.
162.
• Количественной мерой электрического токаслужит сила тока I — скалярная физическая
величина, определяемая электрическим
зарядом, проходящим через поперечное
сечение проводника в единицу времени:
dQ
I
.
dt
• Ток, сила и направление которого не
изменяются со временем, называется
постоянным. Для постоянного тока
Q
I ,
t
163.
• Физическая величина, определяемая силойтока, проходящего через единицу площади
поперечного сечения проводника,
перпендикулярного направлению тока,
называется плотностью тока:
dI
j
.
dS
• сила тока
dQ
I
ne v S ,
dt
• плотность тока
j ne v .
(4.1)
164.
• Сила тока сквозь произвольную поверхностьS определяется как поток вектора j , т. е.
I j dS ,
dS n dS
(4.2)
S
• n — единичный вектор нормали
к площадке
dS, составляющей с вектором j
угол α .
165.
Сторонние силы.Электродвижущая сила и напряжение
• Если в цепи на носители тока действуют только
силы электростатического поля, то происходит
перемещение носителей (они предполагаются
положительными) от точек с большим
потенциалом к точкам с меньшим потенциалом.
• Это приведет к выравниванию потенциалов во
всех точках цепи и к исчезновению электрического
поля.
• Поэтому для существования постоянного тока
необходимо наличие в цепи устройства,
способного создавать и поддерживать разность
потенциалов за счет работы сил
неэлектростатического происхождения.
• Такие устройства называются источниками тока.
166.
Силы неэлектростатического происхождения,действующие на заряды со стороны
источников тока, называются сторонними.
Под действием создаваемого поля сторонних
сил электрические заряды движутся внутри
источника тока против сил
электростатического поля, благодаря чему
на концах цепи поддерживается разность
потенциалов и в цепи течет постоянный
электрический ток.
Сторонние силы совершают работу по
перемещению электрических зарядов.
167.
• Физическая величина, определяемаяработой, совершаемой сторонними силами
при перемещении единичного
положительного заряда, называется
электродвижущей силой (э. д. с.) ,
действующей в цепи:
А / Q0 .
(4.3)
• Эта работа производится за счет энергии,
затрачиваемой в источнике тока, поэтому
величину можно также называть
электродвижущей силой источника тока,
включенного в цепь.
168.
• Сторонняя сила, действующая на заряд Qo,может быть выражена как
FCT ECT Q0 ,
• где ECT — напряженность поля сторонних
сил.
• Работа же сторонних сил по перемещению
заряда Qo на замкнутом участке цепи равна
A FCT dl Q0 ECT dl .
(4.4)
169.
• Разделив (4.4) на Qo, получим выражениедля э.д.с, действующей в цепи:
ЕСТ dl ,
• т. е. э.д.с, действующая в замкнутой цепи,
может быть определена как циркуляция
вектора напряженности поля сторонних сил.
Э.д.с, действующая на участке 1—2, равна
12 ECT dl .
2
1
(4.5)
170.
• На заряд Qo помимо сторонних силдействуют также силы электростатического
поля. Таким образом, результирующая сила,
действующая в цепи на заряд Qo, равна
F FCT Fe Q0 (ECT E) .
• Работа, совершаемая результирующей
силой над зарядом Qo на участке 1—2,
равна
2
A12 Q0 ECT dl Q0 E dl .
2
1
1
171.
• Используя выражения (4.5) и (2.8), можем записатьA12 Q0 12 Q0 ( 1 2 ) .
(4.6)
• Для замкнутой цепи работа электростатических
сил равна нулю (см. §83), поэтому
A12 Q0 12 .
• Напряжением U на участке 1—2 называется
физическая величина, определяемая работой,
совершаемой суммарным полем
электростатических и сторонних сил при
перемещении единичного положительного заряда
на данном участке цепи.
172.
• Таким образом, согласно (4.6),U12 1 2 12.
• Понятие напряжения является обобщением
понятия разности потенциалов:
• напряжение на концах участка цепи равно
разности потенциалов в том случае, если на
этом участке не действует э.д.с, т. е.
сторонние силы отсутствуют.
173.
Закон Ома.Сопротивление проводников
• Немецкий физик Г. Ом экспериментально
установил, что сила тока I, текущего по
однородному металлическому проводнику (т. е.
проводнику, в котором не действуют сторонние
силы), пропорциональна напряжению U на концах
проводника:
(4.7)
I U / R,
• где R — электрическое сопротивление проводника.
Уравнение (98.1) выражает закон Ома для
участка цепи (не содержащего источника э.д.с).
174.
• Формула (4.7) позволяет установить единицусопротивления — ом (Ом): 1 Ом — сопротивление
такого проводника, в котором при напряжении 1 В
течет постоянный ток 1 А.
• Величина
G 1/ R
• называется электрической проводимостью
проводника.
• Единица проводимости — сименс (См): 1 См —
проводимость участка электрической цепи
сопротивлением 1 Ом.
• Сопротивление проводника зависит от его
размеров и формы, а также от материала, из
которого он изготовлен.
175.
• Для однородного линейного проводникасопротивление R прямо пропорционально
его длине l и обратно пропорционально
площади его поперечного сечения S:
l
R ,
S
(4.8)
• где — коэффициент пропорциональности,
характеризующий материал проводника.
• Он называется удельным электрическим
сопротивлением.
• Единица удельного электрического
сопротивления — ом-метр (Ом м).
176.
• Закон Ома можно представить вдифференциальной форме. Подставив выражение
для сопротивления (98.2) в закон Ома (98.1),
получим
I 1U
U
,
S l
l
(4.9)
• где величина 1 / , обратная удельному
сопротивлению, называется удельной
электрической проводимостью вещества
проводника. Ее единица— сименс на метр (См/м).
• Формулу (98.3) можно записать в виде
j E.
(4.10)
177.
• Так как в изотропном проводнике носители тока вкаждой точке движутся
в направлении вектора E ,
то направления j и E совпадают.
• Поэтому формулу (4.10) можно записать в виде
j E.
(4.11)
• Выражение (98.5) — закон Ома в
дифференциальной форме, связывающий
плотность тока в любой точке внутри проводника с
напряженностью электрического поля в этой же
точке.
• Это соотношение справедливо и для переменных
полей.
178.
• Опыт показывает, что в первом приближенииизменение удельного сопротивления, а
следовательно, и сопротивления, с температурой
описывается линейным законом:
0 1 t ,
R R0 (1 t ) ,
• где и 0 , R и Ro — соответственно удельные
сопротивления и сопротивления проводника при
t = 0°С, — температурный коэффициент
сопротивления, для чистых металлов (при не
очень низких температурах) близкий к 1/273 К-1.
• Температурную зависимость сопротивления можно
представить в виде
R R0T ,
179.
• Качественная температурная зависимостьсопротивления металла представлена на рисунке
31 (кривая 1).
R
1
2
Тк
Рисунок 31
Т, К
180.
• Впервые это явление, называемоесверхпроводимостью, обнаружено в 1911 г. Г.
Камерлинг-Оннесом для ртути.
• Явление сверхпроводимости объясняется на
основе квантовой теории.
• Практическое использование сверхпроводящих
материалов (в обмотках сверхпроводящих
магнитов, в системах памяти ЭВМ и др.)
затруднено из-за низких их критических
температур.
• Правда, в настоящее время обнаружены и активно
исследуются керамические материалы,
обладающие сверхпроводимостью при
температуре выше 100 К.
• На зависимости электрического сопротивления металлов
от температуры основано действие термометров
сопротивления, которые позволяют по градуированной
взаимосвязи сопротивления от температуры измерять
температуру с точностью до 0,003 К.
181.
• Если на данном участке цепи источник токаотсутствует ( 12= 0), то из (4.22) приходим к закону
Ома для однородного участка цепи (4.7):
I
1 2
R
U
R
• Если же электрическая цепь замкнута, то
выбранные точки 1 и 2 совпадают, 1 2 ;
тогда из (4.22) получаем закон Ома для замкнутой
цепи:
I 12 / R ,
• R — суммарное сопротивление всей цепи.
• В общем случае R = r + R1, где r — внутреннее
сопротивление источника э.д.с, R1 — сопротивление
внешней цепи.
182.
Работа и мощность тока.Закон Джоуля — Ленца
• Рассмотрим однородный проводник, к концам
которого приложено напряжение U. За время dt
через сечение проводника переносится заряд
dq = I dt. Так как ток представляет собой
перемещение заряда dq под действием
электрического поля, то, по формуле (2.6), работа
тока
dA U dQ IU dt .
(4.12)
183.
• Если сопротивление проводника R, то, используязакон Ома (4.7), получим
U
2
dA I R dt
2
R
dt .
(4.13)
• Из (99.1) и (99.2) следует, что мощность тока
2
dA
U
2
P
UI I R
.
dt
R
(4.14)
• Если сила тока выражается в амперах, напряжение — в
вольтах, сопротивление — в омах, то работа тока
выражается в джоулях, а мощность — в ваттах.
184.
• На практике применяются также внесистемныеединицы работы тока:
• ватт-час (Вт ч) и киловатт-час (кВт ч).
• 1 Вт ч -работа тока мощностью в 1 Вт в течение 1
ч: 1 Вт ч = 3600 Вт с = 3,6 103 Дж;
• 1 кВт ч = 103 Вт ч = 3,6 106 Дж.
• Если ток проходит по неподвижному
металлическому проводнику, то вся работа тока
идет на его нагревание и, по закону сохранения
энергии,
dQТ dA.
(4.15)
185.
• Таким образом, используя выражения (4.15), (4.12)и (4.13), получим
dQТ
U
2
dA IU dt I R dt
2
R
dt .
(4.16)
• Выражение (99.5) представляет собой закон
Джоуля — Ленца, экспериментально
установленный независимо друг от друга Дж.
Джоулем и Э. X. Ленцем (русский физик).
• Выделим в проводнике элементарный
цилиндрический объем dV = dS dl (ось цилиндра
совпадает с направлением тока), сопротивление
которого
dl
R
dS
186.
• По закону Джоуля — Ленца, за время dt в этомобъеме выделится теплота
dQТ
dl
2
I R dt
( jdS )2 dt j 2dV dt .
dS
• Количество теплоты, выделяющееся за единицу
времени в единице объема, называется удельной
тепловой мощностью тока. Она равна
2
w j .
(4.17)
• Используя дифференциальную форму закона Ома
(j = γE) и соотношение 1 / , получим
w
2
jE E .
(4.18)
187.
• Формулы (4.17) и (4.18) являются обобщеннымвыражением закона Джоуля — Ленца в
дифференциальной форме, пригодным для
любого проводника.
• Тепловое действие тока находит широкое
применение в технике, которое началось с
открытия в 1873 г. русским инженером А. Н.
Лодыгиным (1847—1923) лампы накаливания.
• На нагревании проводников электрическим током
основано действие электрических муфельных
печей, электрической дуги (открыта русским
инженером В. В. Петровым (1761 —1834)),
контактной электросварки, бытовых
электронагревательных приборов и т. д.
188.
Электрические цепипостоянного тока
Лекция 8
189.
Закон Ома для неоднородного участкацепи
• Мы рассматривали закон Ома (см. (4.7)) для
однородного участка цепи, т. е. такого, в котором
не действует э.д.с. (не действуют сторонние силы).
• Теперь рассмотрим неоднородный участок цепи,
где действующую э.д.с. на участке 1—2 обозначим
через 12 , а приложенную на концах участка
разность потенциалов — через 1 2 .
• Работа сил, совершаемая при перемещении
заряда Qo на участке 1—2, согласно (4.6),
А12 Q0 12 Q0 ( 1 2 ) .
(4.19)
190.
• Если э.д.с. способствует движению положительныхзарядов в выбранном направлении (в направлении
1—2), то 12 > 0.
• Если э.д.с. препятствует движению положительных
зарядов в данном направлении, то 12 < 0.
• За время t в проводнике выделяется теплота (см.
(4.16))
QТ I 2 Rt IR (It) IRQ0 . (4.20)
• Из формул (4.19) и (4.20) получим
IR ( 1 2 ) 12 ,
I
1 2 12
R
.
(4.21)
(4.22)
191.
Правила Кирхгофа для разветвленныхцепей
• Обобщенный закон Ома (см. (4.21)) позволяет
рассчитать практически любую сложную цепь.
• Однако непосредственный расчет разветвленных
цепей, содержащих несколько замкнутых контуров
(контуры могут иметь общие участки, каждый из
контуров может иметь несколько источников э.д.с.
и т. д.), довольно сложен.
• Эта задача решается более просто с помощью
двух правил Кирхгофа.
• Любая точка разветвления цепи, в которой сходится не
менее трех проводников с током, называется узлом. При
этом ток, входящий в узел, считается положительным, а
ток, выходящий из узла,— отрицательным.
192.
• Первое правило Кирхгофа: алгебраическаясумма токов, сходящихся в узле, равна нулю
I k 0.
k
• Например, для рисунке 148 первое правило
Кирхгофа запишется так:
I1
I1 I 2 I 3 I 4 I 5 0 .
I5
I2
Первое правило Кирхгофа
вытекает из закона сохранения
электрического заряда.
I3
I4
Рисунок 32
193.
• Второе правило Кирхгофа получается изобобщенного закона Ома для разветвленных
цепей. Рассмотрим контур, состоящий из трех
участков (рис. 33).
В
ε2,R2,I2
ε1,R1,I1
А
С
ε 3,R3,I3
Рисунок 33
194.
• Направление обхода по часовой стрелке примемза положительное, отметив, что выбор этого
направления совершенно произволен.
• Все токи, совпадающие по направлению с
направлением обхода контура, считаются
положительными, не совпадающие с
направлением обхода — отрицательными.
• Источники э.д.с. считаются положительными, если
они создают ток, направленный в сторону обхода
контура.
• Применяя к участкам закон Ома (4.21), можно
записать:
I1 R1 A B 1 ,
I 2 R2 B C 2 ,
I 3 R3 C A 3 .
195.
• Складывая почленно эти уравнения, получимI1 R1 I 2 R2 I 3 R3 1 2 3 .
(4.23)
• Уравнение (4.23) выражает второе правило
Кирхгофа: в любом замкнутом контуре,
произвольно выбранном в разветвленной
электрической цепи, алгебраическая сумма
произведений сил токов на сопротивления
соответствующих участков этого контура равна
алгебраической сумме э.д.с., встречающихся в
этом контуре:
I i Ri k .
i
k
(4.24)
196.
• При расчете сложных цепей постоянного тока сприменением правил Кирхгофа необходимо:
• 1. Выбрать произвольное направление токов на всех
участках цепи; действительное направление токов
определяется при решении задачи: если искомый ток
получится положительным, то его направление было
выбрано правильно, отрицательным — его истинное
направление противоположно выбранному.
• 2. Выбрать направление обхода контура и строго его
придерживаться; произведение IR положительно, если ток
на данном участке совпадает с направлением обхода, и
наоборот; э.д.с, действующие по выбранному направлению
обхода, считаются положительными, против —
отрицательными.
• 3. Составить столько уравнений, чтобы их число было
равно числу искомых величин (в систему уравнений
должны входить все сопротивления и э.д.с.
рассматриваемой цепи); каждый рассматриваемый контур
должен содержать хотя бы один элемент, не содержащийся
в предыдущих контурах, иначе получатся уравнения,
являющиеся простой комбинацией уже составленных.
197.
• В качестве примера использования правилКирхгофа рассмотрим схему (рис. 34)
измерительного моста Уитстона
С
I1
I2
IG
R1
А
G
I4
R4
Ir
r
R2
В
I3
R3
RG
D
ε
Рисунок 34
198.
• Для узлов А, В и С, применяя первое правилоКирхгофа, получим
I r I1 I 4 0 ,
I2 I3 Ir 0,
I1 I 2 I G 0 .
(4.25)
• Для контуров ACBA, ACDA и СВDC, согласно
второму правилу Кирхгофа, можно записать:
I r r I1 R1 I 2 R2 ,
I1 R1 I G RG I 4 R4 0 ,
I 2 R2 I 3 R3 I G RG 0 .
(4.26)
199.
• Если известны все сопротивления и э.д.с, то,решая полученные шесть уравнений, можно найти
неизвестные токи. Изменяя известные
сопротивления R2, R3 и R4, можно добиться того,
чтобы ток через гальванометр был равен нулю
( I G = 0). Тогда из (4.25) найдем
I1 I 2 ,
I3 I4 ,
(4.27)
• а из (4.26) получим
I1 R1 I 4 R4 ,
I 2 R2 I 3 R3 .
(4.28)
200.
• Из (4.27) и (4.28) вытекает, чтоR1 R2
,
R4 R3
R2 R4
R1
.
R3
(4.29)
• Таким образом, в случае равновесного моста
( I G = 0) при определении искомого сопротивления
R1
э.д.с. батареи, сопротивления батареи и
гальванометра роли не играют.
• На практике обычно используется реохордный
мост Уитстона (рис. 35).
201.
R1А
R2
G
R4
l4
R3
С
ε
Рисунок 35
l3
В
202.
• Сопротивления R3 и R4 представляют собойдлинную однородную проволоку (реохорд) с
большим удельным сопротивлением.
• В этом случае отношение R3/R4 можно заменить
отношением l 3 / l 4 . Тогда, используя выражение
(4.29), можно записать
l4
R1 R2 .
l3
(4.30)
• Длины l 3 и l 4 легко измеряются по шкале, a R2
всегда известно. Поэтому уравнение (4.30)
позволяет определить неизвестное сопротивление
R1.
203.
Токи в различных средахЛекция 9
204.
Электрические токи в металлах, вакууме игазах
Элементарная классическая теория
электропроводности металлов
Носителями тока в металлах являются свободные
электроны, т. е. электроны, слабо связанные с
ионами кристаллической решетки металла.
Существование свободных электронов в металлах
можно объяснить следующим образом: при
образовании кристаллической решетки металла
валентные электроны, сравнительно слабо
связанные с атомными ядрами, отрываются от
атомов металла, становятся «свободными» и могут
перемещаться по всему объему.
205.
• Таким образом, в узлах кристаллической решеткирасполагаются ионы металла, а между ними
хаотически движутся свободные электроны,
образуя своеобразный электронный газ,
обладающий, согласно электронной теории
металлов, свойствами идеального газа.
• По теории Друде — Лоренца, электроны обладают
такой же энергией теплового движения, как и
молекулы одноатомного газа. Поэтому, применяя
выводы молекулярно-кинетической, можно найти
среднюю скорость теплового движения
электронов,
которая для T = 300 К
u
8
kT
/(
m
)
,
e
равна 1,1 105 м/с.
206.
• Тепловое движение электронов, являясьхаотическим, не может привести к возникновению
тока.
• При наложении внешнего электрического поля на
металлический проводник кроме теплового
движения электронов возникает их упорядоченное
движение, т. е. возникает электрический ток.
• Среднюю скорость v упорядоченного движения
электронов можно оценить по формуле (4.1) для
плотности тока: j = ne v .
• Выбрав допустимую плотность тока, например для
медных проводов107 А/м2, получим, что при
концентрации носителей тока n = 8 1028 м-3
средняя скорость упорядоченного движения
электронов равна 7,8 10-4 м/с.
207.
• Следовательно, даже при очень большихплотностях тока средняя скорость упорядоченного
движения электронов, обусловливающего
электрический ток, значительно меньше их
скорости теплового движения. Поэтому их
результирующую скорость можно заменять
скоростью теплового движения.
• Казалось бы, полученный результат противоречит
факту практически мгновенной передачи
электрических сигналов на большие расстояния.
Дело в том, что замыкание электрической цепи
влечет за собой распространение электрического
поля со скоростью с (с = 3 108 м/с).
• Поэтому электрический ток возникает в цепи
практически одновременно с ее замыканием.
208.
Вывод основных законов электрическоготока в классической теории
электропроводности металлов
• 1. Закон Ома. Пусть в металлическом проводнике
существует электрическое поле напряженностью Е
= const.
• Co стороны поля заряд е испытывает действие
силы F = eE и приобретает ускорение
a = F/m = еЕ/m.
• Таким образом, во время свободного пробега
электроны движутся равноускоренно, приобретая к
концу свободного пробега скорость
vmax eE t / m ,
209.
• Согласно теории Друде, в конце свободногопробега электрон, сталкиваясь с ионами решетки,
отдает им накопленную в поле энергию, поэтому
скорость его упорядоченного движения становится
равной нулю.
• Следовательно, средняя скорость направленного
движения электрона
v (vmax 0) / 2 eE t /(2m) .
(5.1)
• Классическая теория не учитывает распределения
электронов по скоростям, поэтому среднее время
свободного пробега определяется средней длиной
свободного пробега и средней скоростью движения
электронов относительно кристаллической решетки
проводника, равной
+
v
u
210.
• Посколькуv u , поэтому
t l /u.
Подставив значение
t
в формулу (5.1), получим
v eE l /(2m u ) .
Плотность тока в металлическом проводнике,
2
по (4.1),
ne l
j ne v
2m u
E,
откуда видно, что плотность тока пропорциональна
напряженности поля, т. е. получили закон Ома в
дифференциальной форме (ср. с (4.10)).
211.
• Коэффициент пропорциональности между j и Еесть не что иное, как удельная проводимость
материала
2
ne l
,
2m u
(5.2)
• которая тем больше, чем больше концентрация
свободных электронов и средняя длина их
свободного пробега.
• 2. Закон Джоуля — Ленца. К концу свободного
пробега электрон под действием поля приобретает
дополнительную кинетическую энергию
2
2
2
mvmax e l
2.
(5.3)
Eк
E
2
2
2m u
212.
• При соударении электрона с ионом эта энергияполностью передается решетке и идет на
увеличение внутренней энергии металла, т. е. на
его нагревание.
• За единицу времени электрон испытывает с
узлами решетки в среднем z столкновений:
z u /l .
(5.4)
• Если n — концентрация электронов, то в единицу
времени происходит n z столкновений и решетке
передается энергия
w n z Eк ,
(5.5)
• которая идет на нагревание проводника.
213.
• Подставив (5.3) и (5.4) в (5.5), получим, такимобразом, энергию, передаваемую решетке в
единице объема проводника за единицу времени,
2
ne l 2
w
E .
2m u
(5.6)
• Величина w называется удельной тепловой
мощностью тока.
• Коэффициент пропорциональности между w и Е2
по (5.2) есть удельная проводимость γ;
следовательно, выражение (5.6) — закон Джоуля
— Ленца в дифференциальной форме (ср. с
(4.18)).
214.
• 3. Закон Видемана — Франца. Металлы обладаюткак большой электропроводностью, так и высокой
теплопроводностью.
• Это объясняется тем, что носителями тока и теплоты в
металлах являются одни и те же частицы — свободные
электроны, которые, перемещаясь в металле, переносят не
только электрический заряд, но и присущую им энергию
хаотического теплового движения, т. е. осуществляют
перенос теплоты.
• Видеманом и Францем в 1853 г. экспериментально
установлен закон, согласно которому отношение
теплопроводности (λ) к удельной проводимости (γ) для всех
металлов при одной и той же температуре одинаково и
увеличивается пропорционально термодинамической
температуре: / T ,
• где β — постоянная, не зависящая от рода металла.
215.
• Элементарная классическая теорияэлектропроводности металлов позволила найти
значение : β = 3(k/е)2, где k — постоянная
Больцмана. Это значение хорошо согласуется с
опытными данными.
• Однако Лоренц, применив к электронному газу
статистику Максвелла — Больцмана, учтя тем
самым распределение электронов по скоростям,
получил β = 2 (k/е)2, что привело к резкому
расхождению теории с опытом.
• Таким образом, классическая теория
электропроводности металлов объяснила законы
Ома и Джоуля — Ленца, а также дала
качественное объяснение закона Видемана —
Франца.
• Но некоторые её результаты не согласуются с
опытом.
216.
• Температурная зависимость сопротивления.• Из формулы удельной проводимости (5.2) следует,
что сопротивление металлов должно возрастать
пропорционально T (в (103.2) n и l от
температуры не зависят, а u ~ T ).
• Этот вывод электронной теории противоречит
опытным данным, согласно которым R~T.
• Оценка средней длины свободного пробега
электронов в металлах. Чтобы по формуле (5.2)
получить γ, совпадающие с опытными значениями,
надо принимать l значительно больше истинных,
иными словами, предполагать, что электрон
проходит без соударений с ионами решетки сотни
междоузельных расстояний, что не согласуется с
теорией Друде — Лоренца.
217.
• Теплоемкость металлов.• Теплоемкость металла складывается из теплоемкости
его кристаллической решетки и теплоемкости
электронного газа.
• Поэтому атомная (т. е. рассчитанная на 1 моль)
теплоемкость металла должна быть значительно
большей, чем атомная теплоемкость диэлектриков, у
которых нет свободных электронов.
• Согласно закону Дюлонга и Пти, теплоемкость
3 R
одноатомного кристалла равна 3R. Учтем, что
2
теплоемкость одноатомного электронного газа равна
. Тогда атомная теплоемкость металлов должна быть
близка к 4,5R.
• Однако опыт доказывает, что она равна 3R, т. е. для
металлов, так же как и для диэлектриков, хорошо
выполняется закон Дюлонга и Пти.
218.
• Следовательно, наличие электроновпроводимости практически не сказывается
на значении теплоемкости, что не
объясняется классической электронной
теорией.
• Указанные расхождения теории с опытом
можно объяснить тем, что движение
электронов в металлах подчиняется не
законам классической механики, а законам
квантовой механики и, следовательно,
поведение электронов проводимости надо
описывать не статистикой Максвелла —
Больцмана, а квантовой статистикой.
219.
• Этим и объясняются затруднения элементарнойклассической теории.
• Надо, однако, отметить, что классическая
электронная теория не утратила своего значения и
до настоящего времени, так как во многих случаях
(например, при малой концентрации электронов
проводимости и высокой температуре) она дает
правильные качественные результаты и является
по сравнению с квантовой теорией простой и
наглядной.
220.
Ионизация газов. Несамостоятельныйгазовый разряд
• Газы при не слишком высоких температурах и при
давлениях, близких к атмосферному, являются
хорошими изоляторами.
• Это объясняется тем, что газы при обычных
условиях состоят из нейтральных атомов и
молекул и не содержат свободных зарядов
(электронов и ионов).
• Газ становится проводником электричества, когда
некоторая часть его молекул ионизуется, т. е.
произойдет расщепление нейтральных атомов и
молекул на ионы и свободные электроны.
221.
• При ионизации газов под действием какого-либоионизатора происходит вырывание из электронной
оболочки атома или молекулы одного или
нескольких электронов, что приводит к
образованию свободных электронов и
положительных ионов.
• Электроны могут присоединяться к нейтральным
молекулам и атомам, превращая их в
отрицательные ионы.
• Следовательно, в ионизованном газе имеются
положительные и отрицательные ионы и
свободные электроны.
• Прохождение электрического тока через газы
называется газовым разрядом.
222.
• Ионизация газов может происходить под действиемразличных ионизаторов: сильный нагрев
(столкновения быстрых молекул становятся
настолько сильными, что они разбиваются на ионы),
короткое электромагнитное излучение
(ультрафиолетовое, рентгеновское и -излучения),
корпускулярное излучение (потоки электронов,
протонов, -частиц) и т. д.
• Для того чтобы выбить из молекулы (атома) один
электрон, необходимо затратить определенную
энергию, называемую энергией ионизации,
значения которой для атомов различных веществ
лежат в пределах 4 25 эВ.
• Одновременно с процессом ионизации газа всегда
идет и обратный процесс — процесс
рекомбинации: положительные и отрицательные
ионы, положительные ионы и электроны, встречаясь,
воссоединяются между собой с образованием
нейтральных атомов и молекул.
223.
• Строго говоря, электропроводность газа нулю неравна никогда, так как в нем всегда имеются
свободные заряды, образующиеся в результате
действия на газы излучения радиоактивных веществ,
имеющихся на поверхности Земли, а также
космического излучения.
• Эта незначительная электропроводность воздуха
(интенсивность ионизации под действием указанных
факторов невелика) служит причиной утечки зарядов
наэлектризованных тел даже при хорошей их
изоляции.
• Характер газового разряда определяется составом
газа, его температурой и давлением, размерами,
конфигурацией и материалом электродов,
приложенным напряжением, плотностью тока.
224.
• Рассмотрим цепь, содержащую газовыйпромежуток (рис. 39), подвергающийся
непрерывному, постоянному по интенсивности
воздействию ионизатора.
I
E
mA
А
V
В
С
D
Iнас
R
0
Рисунок 40
Рисунок 39
U
225.
• На участке кривой ОА сила тока возрастаетпропорционально напряжению, т. е. выполняется
закон Ома.
• При дальнейшем увеличении напряжения закон
Ома нарушается: рост силы тока замедляется
(участок АВ) и наконец прекращается совсем
(участок ВС).
• Это происходит, когда все ионы и электроны,
создаваемые внешним ионизатором за единицу
времени, за это же время достигают электродов.
• В результате получаем ток насыщения, значение
которого определяется мощностью ионизатора.
• Разряды, существующие только под действием
внешних ионизаторов, называются
несамостоятельными.
226.
Самостоятельный газовый разряд и еготипы
• Разряд в газе, сохраняющийся после прекращения
действия внешнего ионизатора, называется
самостоятельным.
• при больших напряжениях между электродами
газового промежутка (см. рис. 39) ток сильно
возрастает (участки CD и DE на рис.40).
• При больших напряжениях возникающие под
действием внешнего ионизатора электроны,
сильно ускоренные электрическим полем,
сталкиваясь с нейтральными молекулами газа,
ионизируют их, в результате чего образуются
вторичные электроны и положительные ионы
(процесс 1 на рис.41).
227.
Рисунок 41228.
• Вторичные электроны вновь ионизируют молекулыгаза, и, следовательно, общее количество
электронов и ионов будет возрастать по мере
продвижения электронов к аноду лавинообразно.
Это является причиной увеличения электрического
тока на участке CD (см. рис.40). Описанный
процесс называется ударной ионизацией.
• Однако ударная ионизация под действием
электронов недостаточна для поддержания
разряда при удалении внешнего ионизатора.
• Для этого необходимо, чтобы электронные лавины
«воспроизводились», т. е. чтобы в газе под
действием каких-то процессов возникали новые
электроны (см. рис.41):
229.
• 1) ускоренные полем положительные ионы, ударяясь окатод, выбивают из него электроны (процесс 2);
• 2) положительные ионы, сталкиваясь с молекулами
газа, переводят их в возбужденное состояние; переход
таких молекул в нормальное состояние
сопровождается испусканием фотона (процесс 3);
• 3) фотон, поглощенный нейтральной молекулой,
ионизирует ее, происходит так называемый процесс
фотонной ионизации молекул (процесс 4);
• 4) выбивание электронов из катода под действием
фотонов (процесс 5);
• 5) при значительных напряжениях между электродами
газового промежутка наступает момент, когда
положительные ионы, обладающие меньшей длиной
свободного пробега, чем электроны, приобретают
энергию, достаточную для ионизации молекул газа
(процесс 6), и к отрицательной пластине устремляются
ионные лавины.
230.
• Тогда возникают кроме электронных лавин еще иионные, сила тока растет уже практически без
увеличения напряжения (участок DE на рис.40).
• В результате описанных процессов (1—6) число
ионов и электронов в объеме газа лавинообразно
возрастает и разряд становится самостоятельным,
т. е. сохраняется после прекращения действия
внешнего ионизатора. Напряжение, при котором
возникает самостоятельный разряд, называется
напряжением пробоя.
• В зависимости от давления газа, конфигурации
электродов, параметров внешней цепи можно
говорить о четырех типах самостоятельного
разряда: тлеющем, искровом, дуговом и
коронном.
231.
• 1. Тлеющий разряд возникает при низкихдавлениях.
• Если к электродам, впаянным в стеклянную трубку
длиной 30— 50 см, приложить постоянное
напряжение в несколько сотен вольт, постепенно
откачивая из трубки воздух, то при давлении
5,3 6,7 кПа возникает разряд в виде светящегося
извилистого шнура красноватого цвета, идущего от
катода к аноду.
• При дальнейшем понижении давления шнур
утолщается, и при давлении 13 Па разряд имеет
вид, схематически изображенный на рис.42.
232.
к катоду прилегает тонкий светящийся слой 1 — первое катодное свечение,
или катодная пленка, затем следует темный слой 2 — катодное темное
пространство, переходящее в дальнейшем в светящийся слой 3 — тлеющее
свечение, имеющее резкую границу со стороны катода, постепенно
исчезающую со стороны анода. Оно возникает из-за рекомбинации электронов
с положительными ионами. С тлеющим свечением граничит темный
промежуток 4 — фарадеево темное пространство, за которым следует столб
ионизированного светящегося газа 5 — положительный столб.
1
К
3
2
5
4
Рисунок 42
А
233.
• Положительный столб существенной роли вподдержании разряда не имеет. При уменьшении
расстояния между электродами трубки его длина
сокращается, в то время как катодные части разряда
по форме и величине остаются неизменными.
• В тлеющем разряде особое значение для его
поддержания имеют только две его части: катодное
темное пространство и тлеющее свечение.
• В катодном темном пространстве происходит сильное
ускорение электронов и положительных ионов,
выбивающих электроны с катода (вторичная эмиссия).
В области тлеющего свечения же происходит ударная
ионизация электронами молекул газа. Образующиеся
при этом положительные ионы устремляются к катоду
и выбивают из него новые электроны, которые, в свою
очередь, опять ионизируют газ и т. д. Таким образом
непрерывно поддерживается тлеющий разряд.
234.
• При дальнейшем откачивании трубки придавлении 1,3 Па свечение газа ослабевает и
начинают светиться стенки трубки.
• Электроны, выбиваемые из катода
положительными ионами, при таких разрежениях
редко сталкиваются с молекулами газа и поэтому,
ускоренные полем, ударяясь о стекло, вызывают
его свечение, так называемую
катодолюминесценцию.
• Поток этих электронов исторически получил
название катодных лучей. Если в катоде
просверлить малые отверстия, то положительные
ионы, бомбардирующие катод, пройдя через
отверстия, проникают в пространство за катодом и
образуют резко ограниченный пучок, получивший
название каналовых (или положительных)
лучей, названных по знаку заряда, который они
несут.
235.
• Тлеющий разряд широко используется в технике. Так каксвечение положительного столба имеет характерный для
каждого газа цвет, то его используют в газосветных
трубках для светящихся надписей и реклам (например,
неоновые газоразрядные трубки дают красное свечение,
аргоновые — синевато-зеленое).
• В лампах дневного света, более экономичных, чем
лампы накаливания, излучение тлеющего разряда,
происходящее в парах ртути, поглощается нанесенным
на внутреннюю поверхность трубки флуоресцирующим
веществом (люминофором), начинающим под
воздействием поглощенного излучения светиться.
• Тлеющий разряд используется для катодного
напыления металлов. Вещество катода в тлеющем
разряде вследствие бомбардировки положительными
ионами, сильно нагреваясь, переходит в парообразное
состояние. Помещая вблизи катода различные
предметы, их можно покрыть равномерным слоем
металла.
236.
• 2. Искровой разряд возникает при большихнапряженностях электрического поля ( 3 106 В/м)
в газе, находящемся под давлением порядка
атмосферного. Искра имеет вид ярко светящегося
тонкого канала, сложным образом изогнутого и
разветвленного.
• Объяснение искрового разряда дается на основе
стримерной теории, согласно которой
возникновению ярко светящегося канала искры
предшествует появление слабосветящихся
скоплений ионизованного газа — стримеров.
Стримеры возникают не только в результате
образования электронных лавин посредством
ударной ионизации, но и в результате фотонной
ионизации газа. Лавины, догоняя друг друга,
образуют проводящие мостики из стримеров, по
которым в следующие моменты времени и
устремляются мощные потоки электронов,
образующие каналы искрового разряда.
237.
• Из-за выделения при рассмотренных процессахбольшого количества энергии газ в искровом
промежутке нагревается до очень высокой
температуры (104 К), что приводит к его свечению.
• Быстрый нагрев газа ведет к повышению давления
и возникновению ударных волн, объясняющих —
характерное потрескивание в слабых разрядах и
мощные раскаты грома в случае молнии,
являющейся примером мощного искрового
разряда между грозовым облаком и Землей или
между двумя грозовыми облаками.
• Искровой разряд используется для воспламенения
горючей смеси в двигателях внутреннего сгорания
и предохранения электрических линий передачи от
перенапряжений (искровые разрядники).
238.
• 3. Дуговой разряд. Если после зажиганияискрового разряда от мощного источника
постепенно уменьшать расстояние между
электродами, то разряд становится непрерывным
— возникает дуговой разряд. При этом сила тока
резко возрастает до сотен ампер, а напряжение на
разрядном промежутке падает до нескольких
десятков вольт.
• Дуговой разряд можно получить при низком
напряжении минуя стадию искры. Для этого
электроды сближают до соприкосновения, они
сильно раскаляются электрическим током, потом
их разводят и получают электрическую дугу. По
мере горения дуги угольный катод заостряется, а
на аноде образуется углубление — кратер,
являющийся наиболее горячим местом дуги (3900
К).
239.
• По современным представлениям, дуговой разрядподдерживается за счет высокой температуры
катода из-за интенсивной термоэлектронной
эмиссии, а также термической ионизации молекул,
обусловленной высокой температурой газа.
• Дуговой разряд находит широкое применение в
народном хозяйстве для сварки и резки металлов,
получения высококачественных сталей (дуговая
печь) и освещения (прожекторы, проекционная
аппаратура). Широко применяются также дуговые
лампы с ртутными электродами в кварцевых
баллонах, где дуговой разряд возникает в ртутном
паре при откачанном воздухе. Дуга, возникающая в
ртутном паре, является мощным источником
ультрафиолетового излучения и используется в
медицине (например, кварцевые лампы). Дуговой
разряд при низких давлениях в парах ртути
используется в ртутных выпрямителях для
выпрямления переменного тока.
240.
• 4. Коронный разряд — высоковольтныйэлектрический разряд при высоком
(например, атмосферном) давлении в резко
неоднородном поле вблизи электродов с
большой кривизной поверхности (например,
острия). При напряженности поля вблизи
острия ~ 30 кВ/см вокруг него возникает
свечение, имеющее вид короны, чем и
вызвано название этого вида разряда.
241.
• В зависимости от знака коронирующегоэлектрода различают отрицательную или
положительную корону. В случае
отрицательной короны рождение
электронов, вызывающих ударную
ионизацию молекул газа, происходит за счет
эмиссии их из катода под действием
положительных ионов, в случае
положительной — вследствие ионизации
газа вблизи анода.
242.
• В естественных условиях корона возникаетпод влиянием атмосферного электричества
у вершин мачт (на этом основано действие
молниеотводов), деревьев (Это явление
получило в древности название огней
святого Эльма).
• Вредное действие короны вокруг проводов
высоковольтных линий передачи
проявляется в возникновении вредных токов
утечки. Для их снижения провода
высоковольтных линий делаются толстыми.
Коронный разряд, являясь прерывистым,
становится также источником радиопомех.
243.
• Используется коронный разряд вэлектрофильтрах, применяемых для очистки
промышленных газов от примесей.
• Газ, подвергаемый очистке, движется снизу
вверх в вертикальном цилиндре, по оси
которого расположена коронирующая
проволока. Ионы, имеющиеся в большом
количестве во внешней части короны,
оседают на частицах примеси и увлекаются
полем к внешнему некоронирующему
электроду и на нем оседают.
• Коронный разряд применяется также при
нанесении порошковых и лакокрасочных
покрытий.
244.
Работа выхода электронов изметалла
Эмиссионные явления
Лекция 10
245.
Работа выхода электронов из металла• Как показывает опыт, свободные электроны при
обычных температурах практически не, покидают
металл. Следовательно, в поверхностном слое
металла должно быть задерживающее
электрическое поле, препятствующее выходу
электронов из металла в окружающий вакуум.
• Работа, которую нужно затратить для удаления
электрона из металла в вакуум, называется
работой выхода.
• Укажем две вероятные причины появления работы
выхода:
246.
• 1. Если электрон по какой-то причине удаляется изметалла, то в том месте, которое электрон
покинул, возникает избыточный положительный
заряд и электрон притягивается к
индуцированному им самим положительному
заряду.
• 2. Отдельные электроны, покидая металл,
удаляются от него на расстояния порядка атомных
и создают тем самым над поверхностью металла
«электронное облако».
• Это облако вместе с наружным слоем
положительных ионов решетки образует двойной
электрический слой, поле которого подобно полю
плоского конденсатора.
• Толщина этого слоя равна нескольким
межатомным расстояниям (10-10 — 10-9 м). Он не
создает электрического поля во внешнем
пространстве, но препятствует выходу свободных
электронов из металла.
247.
• Таким образом, электрон при вылете из металладолжен преодолеть задерживающее его
электрическое поле двойного слоя. Разность
потенциалов в этом слое, называемая
поверхностным скачком потенциала,
определяется работой выхода (А) электрона из
металла:
A / e ,
Вне двойного слоя электрическое поле отсутствует,
то потенциал среды равен нулю, а внутри металла
потенциал положителен и равен .
Потенциальная энергия свободного электрона
внутри металла равна –е и является
относительно вакуума отрицательной.
248.
Работа выхода выражается в электрон-вольтах(эВ): 1 эВ равен работе, совершаемой силами поля
при перемещении элементарного электрического
заряда (заряда, равного заряду электрона) при
прохождении им разности потенциалов в 1 В.
Так как заряд электрона равен 1,6 10-19 Кл,
то 1 эВ = 1,6 10-19 Дж.
Работа выхода зависит от химической природы
металлов и от чистоты их поверхности и
колеблется в пределах нескольких электрон-вольт
(например, у калия А = 2,2 эВ, у платины А =6,3
эВ).
Подобрав определенным образом покрытие
поверхности, можно значительно уменьшить
работу выхода. Например, если нанести на
поверхность вольфрама (А = 4,5 эВ) слой оксида
щелочно-земельного металла (Са, Sr, Ba), то
работа выхода снижается до 2 эВ.
249.
Эмиссионные явления и их применение• Если сообщить электронам в металлах энергию,
необходимую для преодоления работы выхода, то
часть электронов может покинуть металл, в
результате чего наблюдается явление испускания
электронов, или электронной эмиссии.
• В зависимости от способа сообщения электронам
энергии различают:
• термоэлектронную,
• фотоэлектронную,
• вторичную электронную и
• автоэлектронную эмиссии.
250.
• I. Термоэлектронная эмиссия — это испусканиеэлектронов нагретыми металлами.
• Концентрация свободных электронов в металлах
достаточно высока, поэтому даже при средних
температурах вследствие распределения
электронов по скоростям (по энергии) некоторые
электроны обладают энергией, достаточной для
преодоления потенциального барьера на границе
металла.
• С повышением температуры число электронов,
кинетическая энергия теплового движения которых
больше работы выхода, растет и явление
термоэлектронной эмиссии становится заметным.
251.
• Исследование закономерностей термоэлектроннойэмиссии можно провести с помощью простейшей
двухэлектродной лампы — вакуумного диода,
представляющего собой откачанный баллон,
содержащий два электрода: катод К и анод А.
• В простейшем случае катодом служит нить из
тугоплавкого металла (например, вольфрама),
накаливаемая электрическим током.
• Анод чаще всего имеет форму металлического
цилиндра, окружающего катод.
• Схема включения диода показана на рисунке 36.
252.
mAR
А
К
V
Rн
Бн
Рисунок 36
Ба
253.
• Если поддерживать температуру накаленногокатода постоянной и снять зависимость анодного
тока Iа от анодного напряжения Ua — вольтамперную характеристику (рис. 37), то
оказывается, что она не является линейной, т. е.
для вакуумного диода закон Ома не выполняется.
• Зависимость термоэлектронного тока I от анодного
напряжения в области малых положительных
значений U описывается законом трех вторых:
3
/
2
I BU ,
• где В — коэффициент, зависящий от формы и
размеров электродов, а также их взаимного
расположения.
254.
IaТ2
I2нас
Т1
I1нас
Т растет
0
Ua
Рисунок 37
255.
• Плотность тока насыщения определяетсяформулой Ричардсона — Дешмана, выведенной
теоретически на основе квантовой статистики:
jнас
A /(kT )
2
CT e
,
• где А — работа выхода электронов из катода, Т —
термодинамическая температура, С — постоянная,
теоретически одинаковая для всех металлов (это
не подтверждается экспериментом, что, повидимому, объясняется поверхностными
эффектами).
• Уменьшение работы выхода приводит к резкому
увеличению плотности тока насыщения.
256.
• Явление термоэлектронной эмиссии используетсяв приборах, в которых необходимо получить поток
электронов в вакууме, например в электронных
лампах, рентгеновских трубках, электронных
микроскопах и т. д.
• Электронные лампы широко применяются в
электро- и радиотехнике, автоматике и
телемеханике для выпрямления переменных
токов, усиления электрических сигналов и
переменных токов, генерирования
электромагнитных колебаний и т. д.
• В зависимости от назначения в лампах
используются дополнительные управляющие
электроды.
257.
• 2. Фотоэлектронная эмиссия — это эмиссияэлектронов из металла под действием света, а
также коротковолнового электромагнитного
излучения (например, рентгеновского).
• 3. Вторичная электронная эмиссия — это
испускание электронов поверхностью металлов,
полупроводников или диэлектриков при
бомбардировке их пучком электронов.
• Вторичный электронный поток состоит из
электронов, отраженных поверхностью (упруго и
неупруго отраженные электроны), и «истинно»
вторичных электронов — электронов, выбитых из
металла, полупроводника или диэлектрика
первичными электронами.
258.
• Отношение числа вторичных электронов к числупервичных, вызвавших эмиссию, называется
коэффициентом вторичной электронной
эмиссии:
n2 / n1 .
• Коэффициент зависит от природы материала
поверхности, энергии бомбардирующих частиц и
их угла падения на поверхность.
• У полупроводников и диэлектриков δ больше, чем
у металлов.
• Это объясняется тем, что в металлах, где
концентрация электронов проводимости велика,
вторичные электроны, часто сталкиваясь с ними,
теряют свою энергию и не могут выйти из металла.
259.
• Явление вторичной электронной эмиссиииспользуется в фотоэлектронных умножителях
(ФЭУ), применяемых для усиления слабых
электрических токов.
• ФЭУ представляет собой вакуумную трубку с
фотокатодом К и анодом А, между которыми
расположено несколько электродов—эмиттеров
(рис. 38).
К
Э
2
Рисунок 38
А
260.
• Электроны, вырванные с фотокатода поддействием света, попадают на эмиттер Э1 пройдя
ускоряющую разность потенциалов между К и Э1.
Из эмиттера Э1 каждым падающим электроном
выбивается электронов.
• Усиленный таким образом электронный поток
направляется на эмиттер Э2, и процесс умножения
повторяется на всех последующих эмиттерах.
Если ФЭУ содержит n эмиттеров, то на аноде А,
называемом коллектором, получается усиленный
в n раз фотоэлектронный ток.
• 4. Автоэлектронная эмиссия — это эмиссия
электронов с поверхности металлов под
действием сильного внешнего электрического
поля.
261.
Список использованныхисточников
Савельев, И.В. Курс физики: учеб. пособие для вузов Т. 1-5/ И. В. Савельев . - 3е изд., стер. - CПб.: Лань, 2007.
Трофимова Т.И. Курс физики: учеб. пособие для вузов / Т. И. Трофимова .- 15-е
изд., стер. - М. : Академия, 2007. - 560 с.
Детлаф, А. А. Курс физики: учеб. пособие для втузов / А. А. Детлаф, Б. М.
Яворский.- 5-е изд., стер. - М.: Академия, 2005. - 720 с.
Иродов, И.Е. Механика. Основные законы [Текст]/ И.Е. Иродов. – М.:
Лаборатория базовых знаний, 2003. – 312 с.
Иродов, И.Е. Физика макросистем. Основные законы [Текст]/ И.Е. Иродов. – М.:
Физматлит, 2001. – 200 с.
Иродов, И.Е. Электромагнетизм. Основные законы [Текст]/ И.Е. Иродов. –
БИНОМ. Лаборатория знаний, 2006. – 320 с.
Иродов, И.Е. Квантовая физика. Основные законы [Текст]/ И.Е. Иродов. – М.:
Лаборатория Базовых знаний, 2001. – 272 с.
Иродов, И.Е. Волновые процессы. Основные законы [Текст]/ И.Е. Иродов. – М.:
Физматлит: Лаборатория Базовых знаний , 2001. – 256 с.



























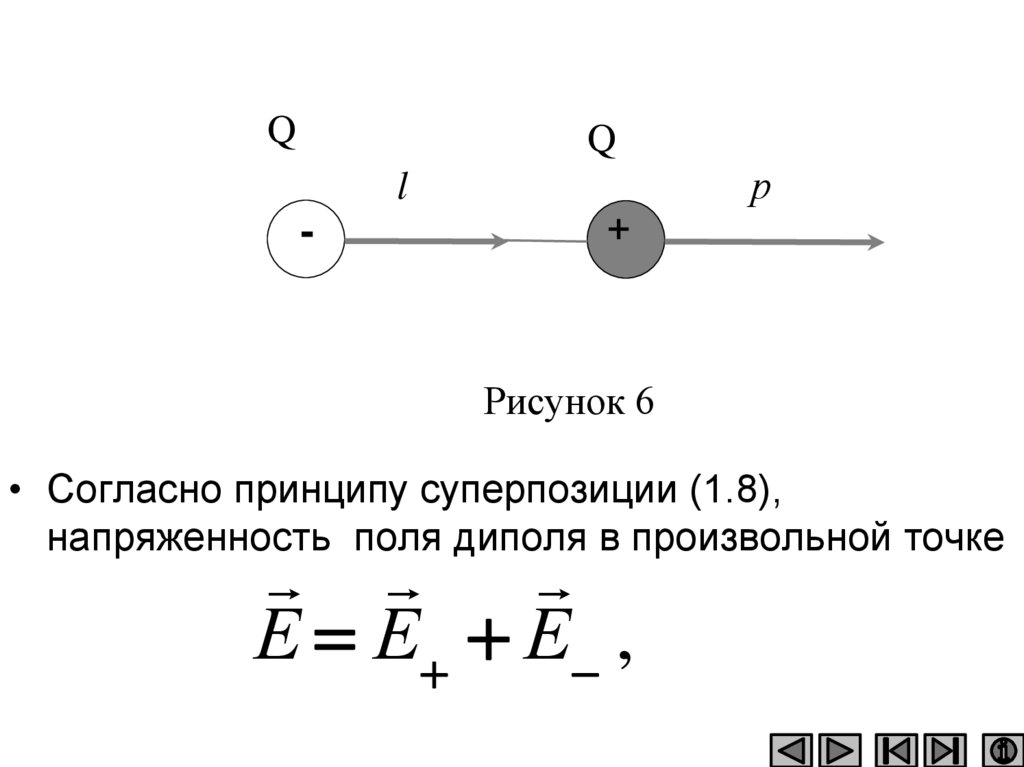
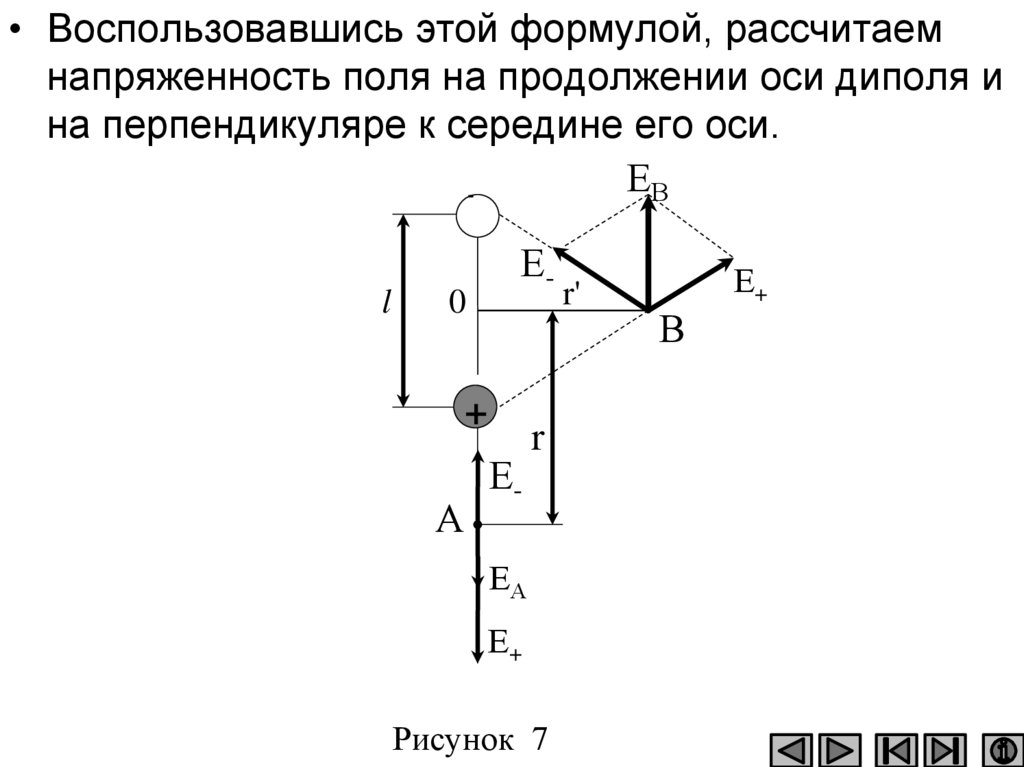





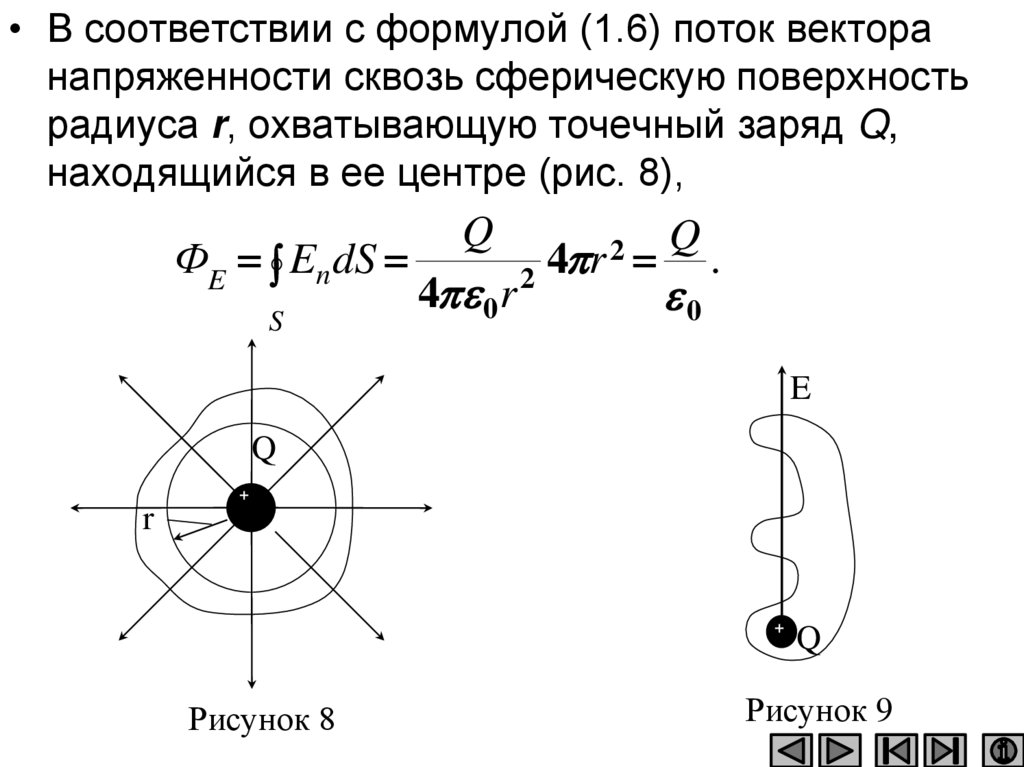







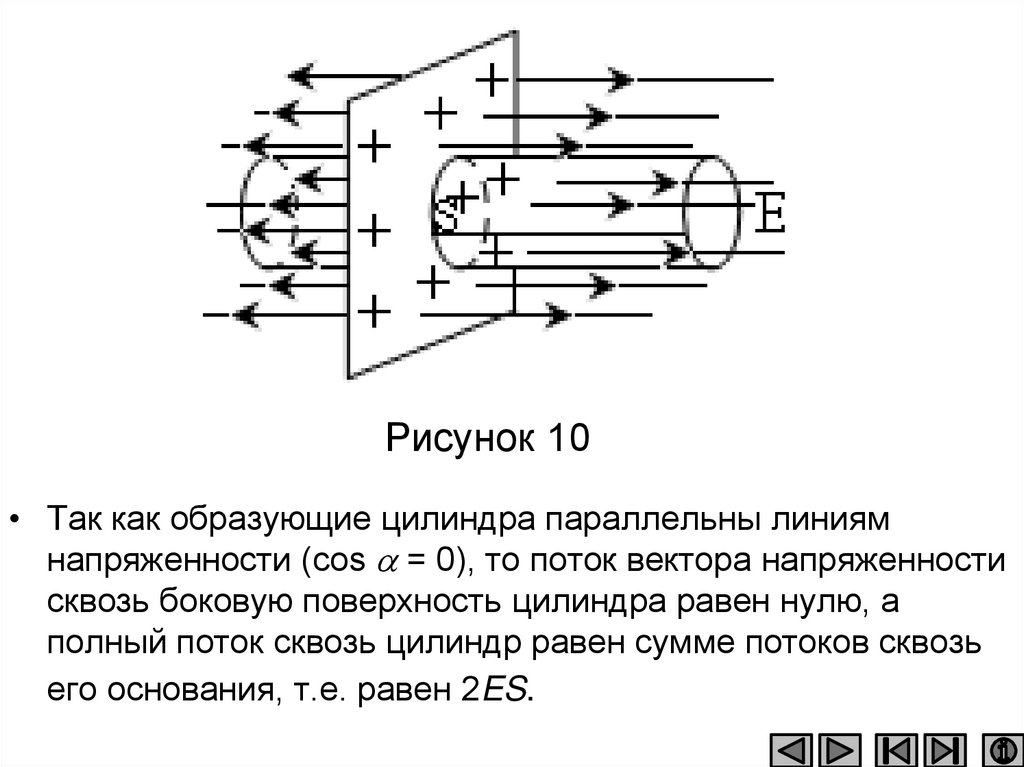

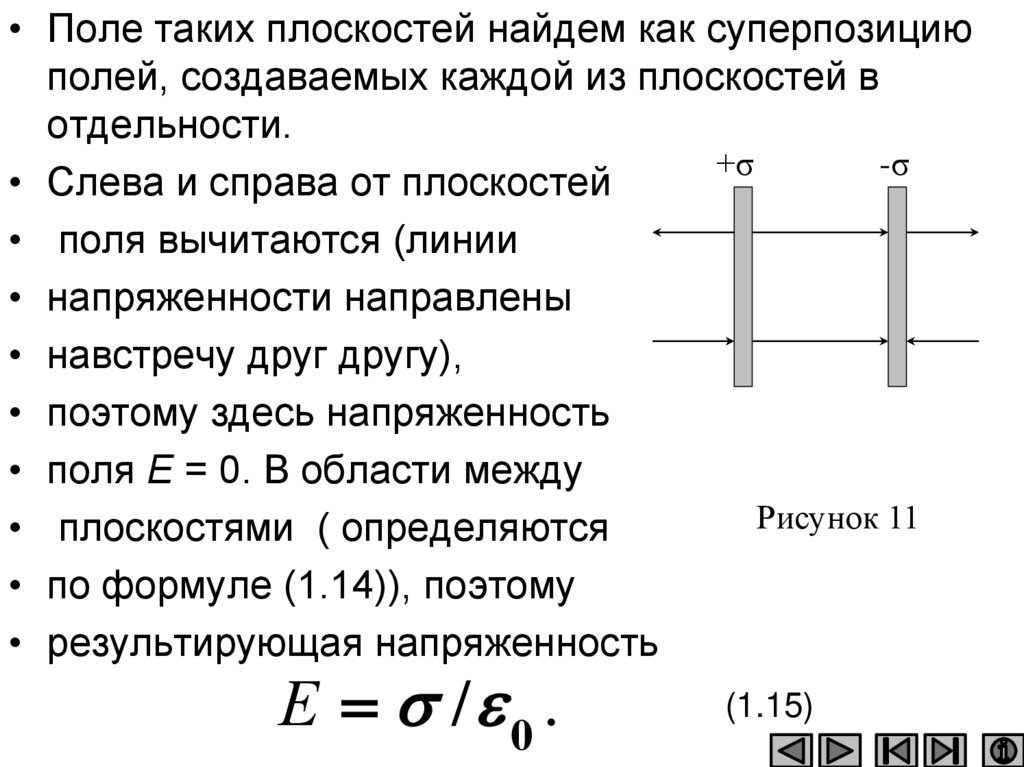


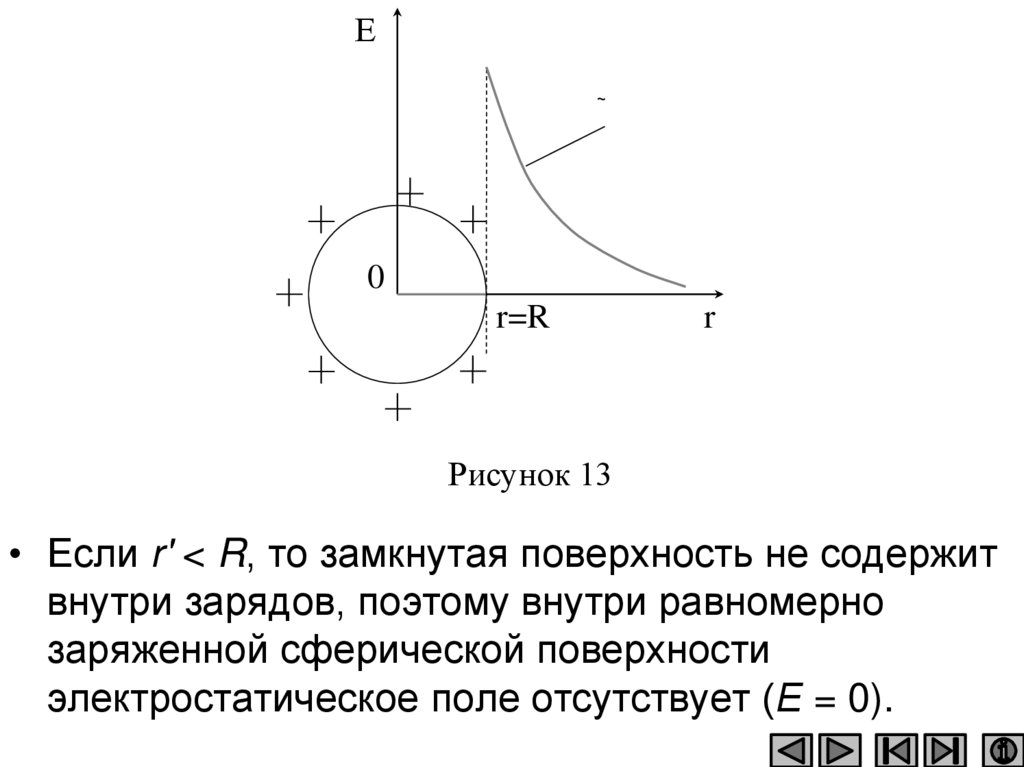

























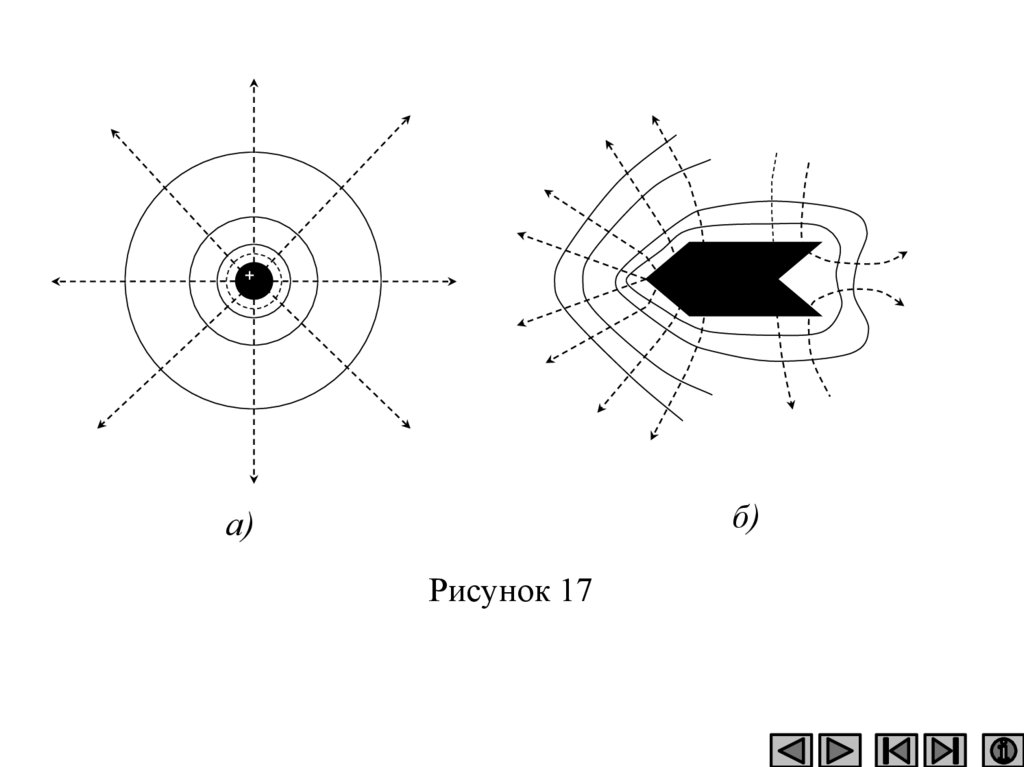
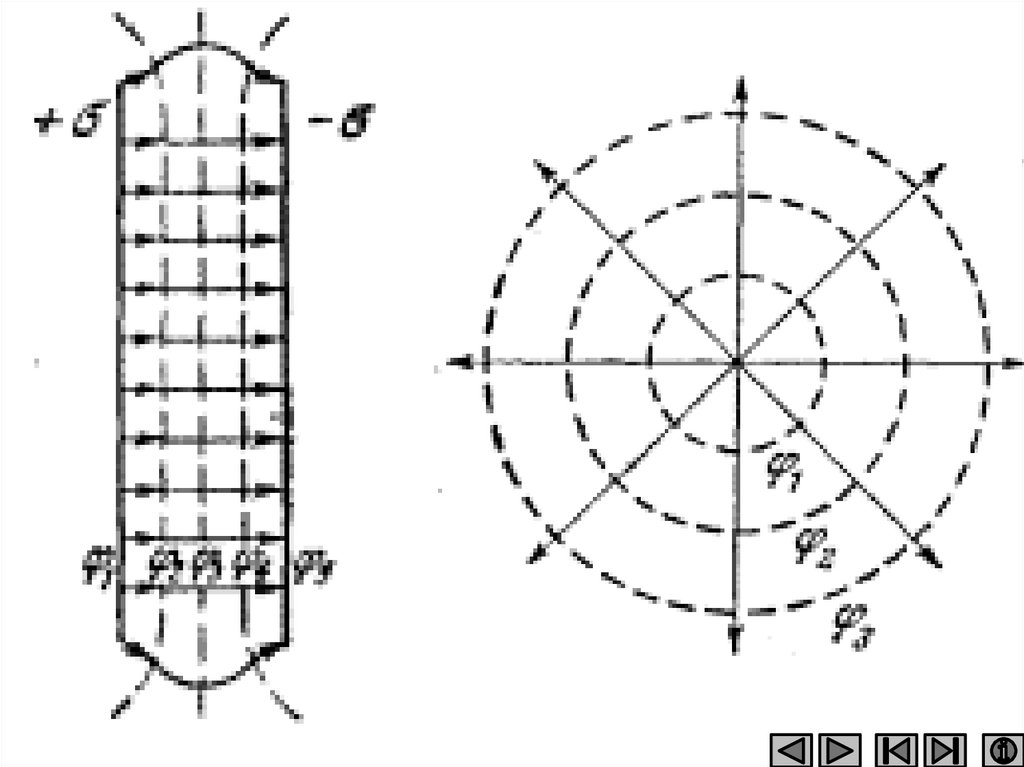
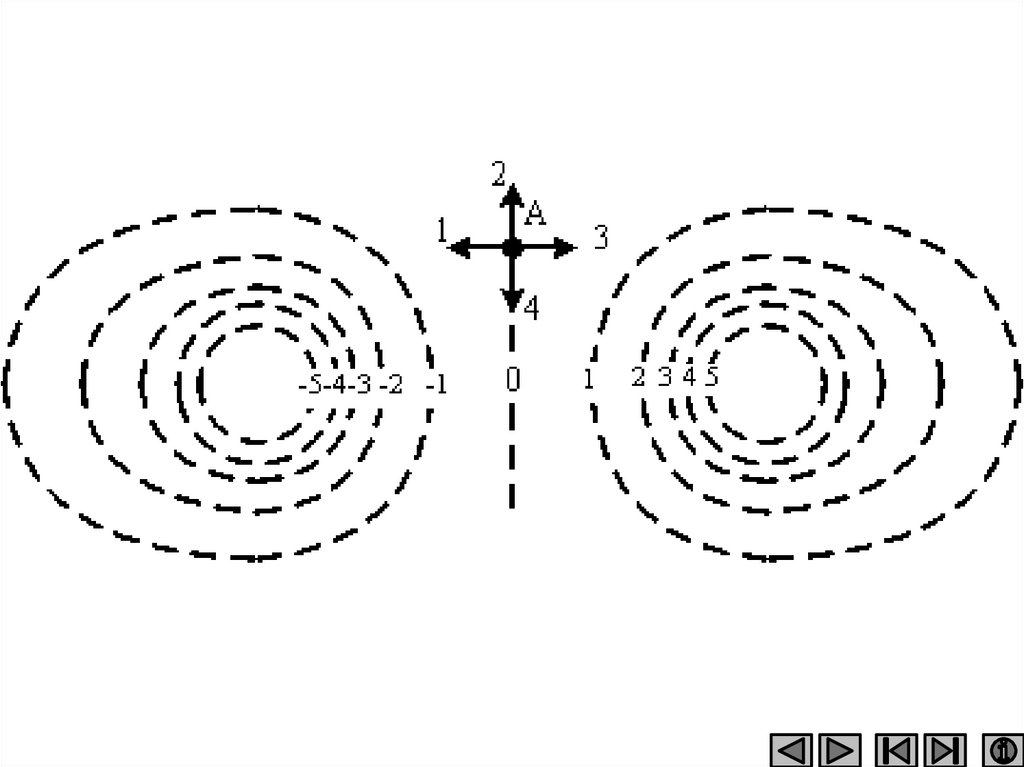


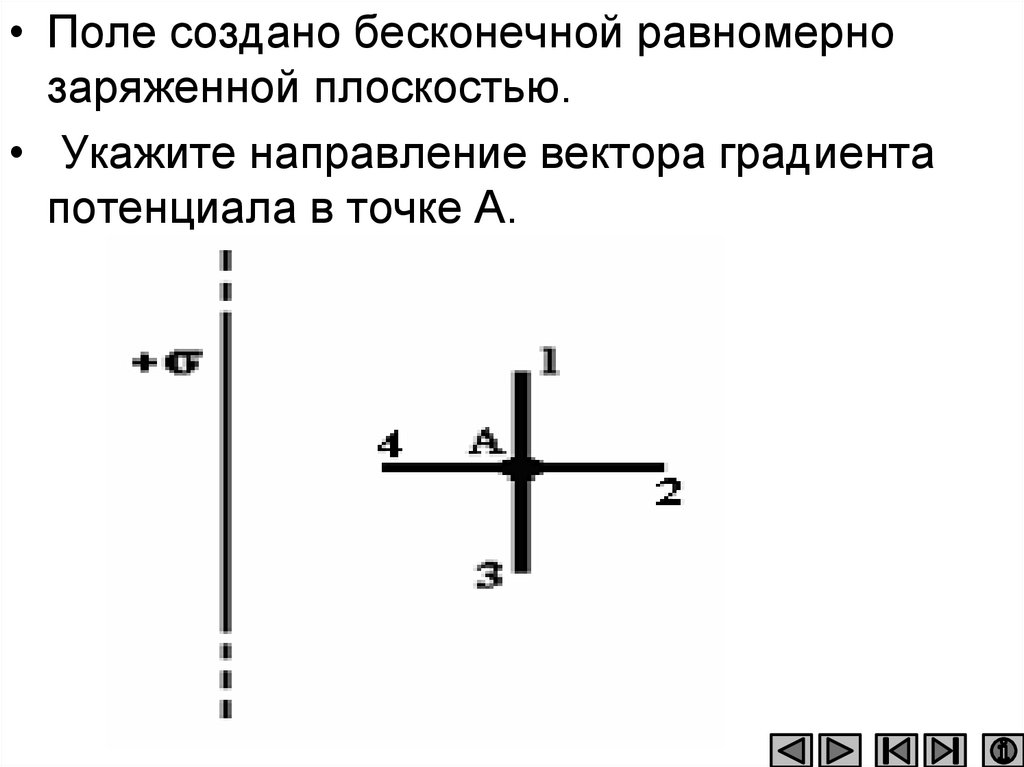

















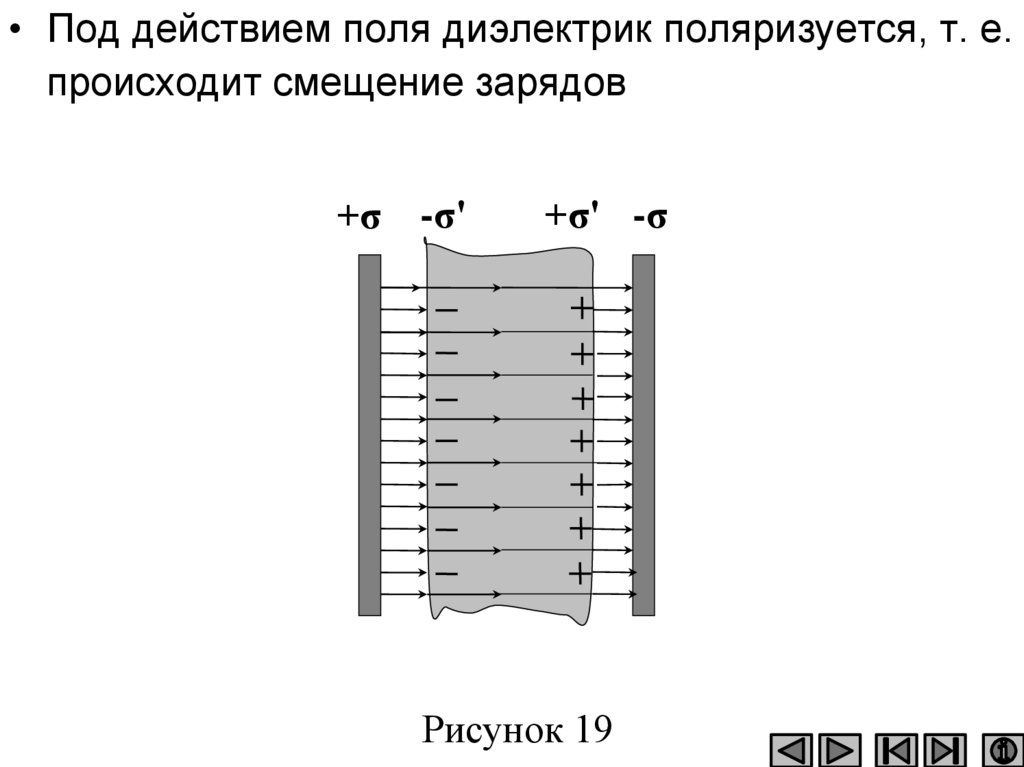











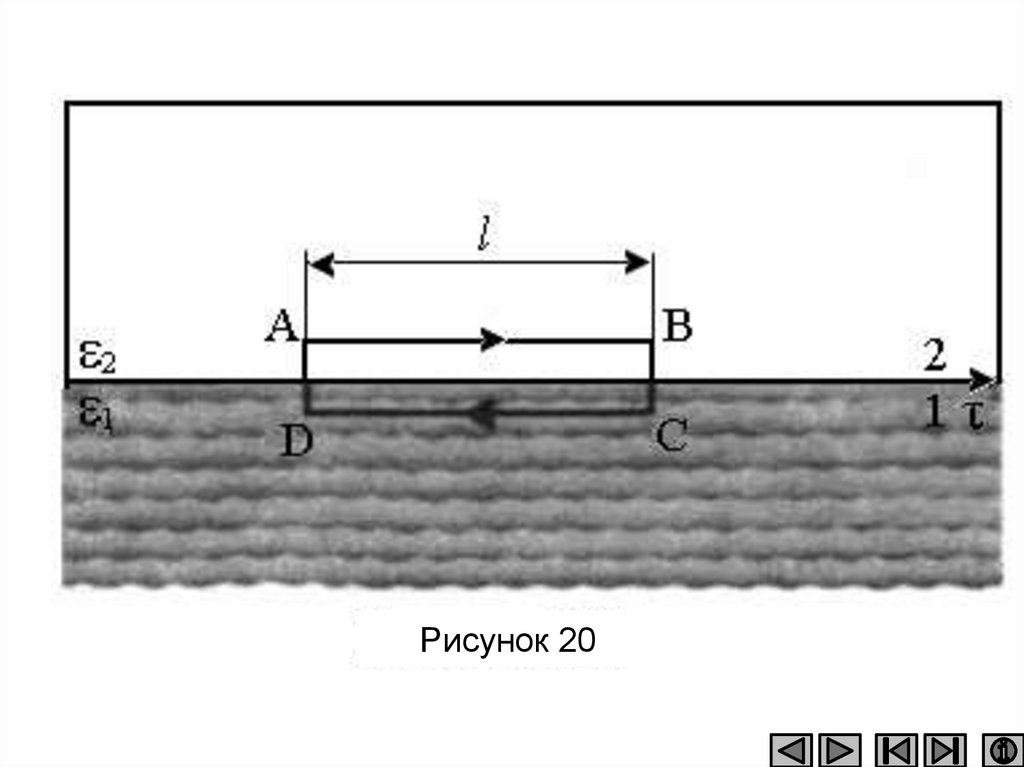





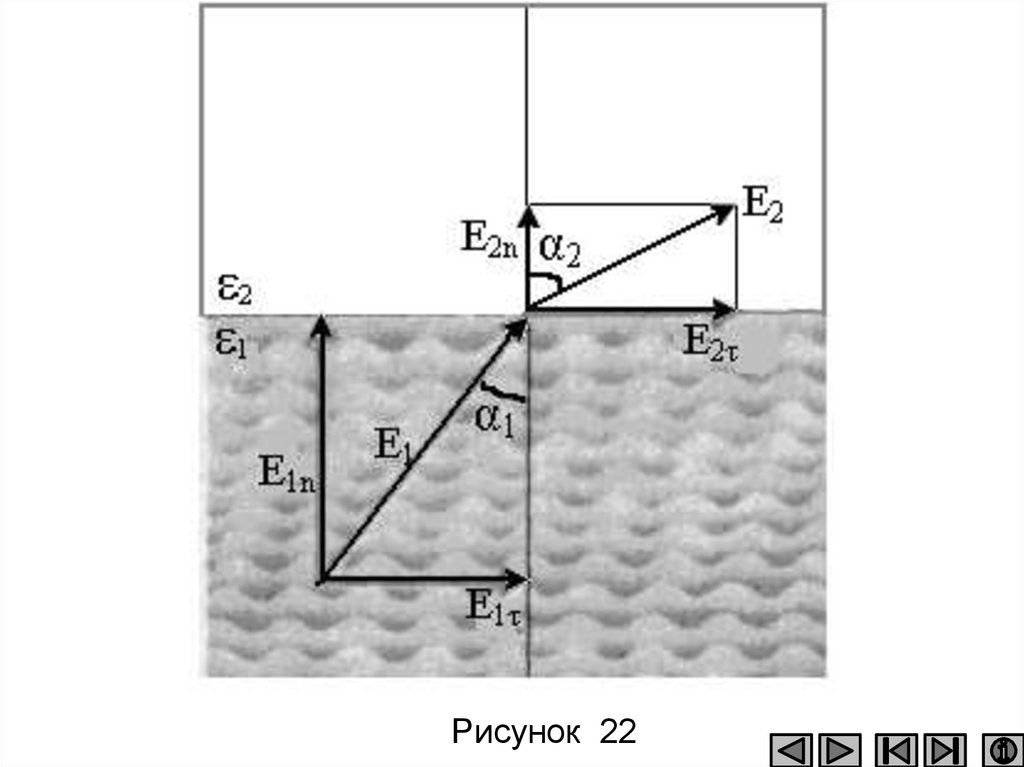


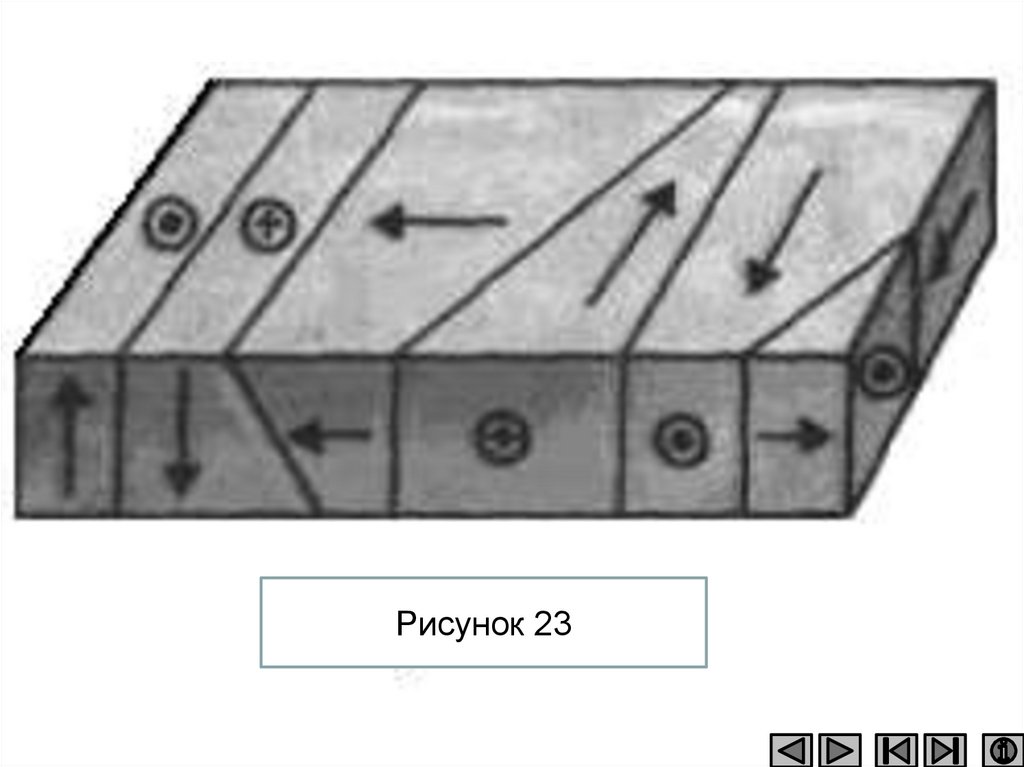









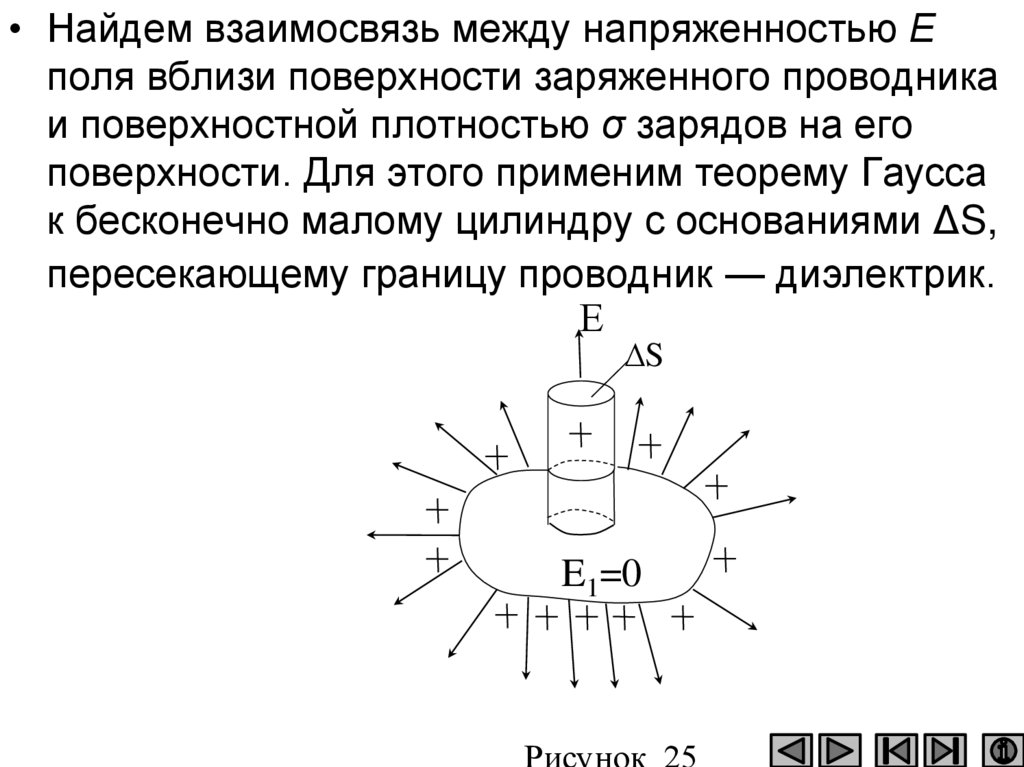

















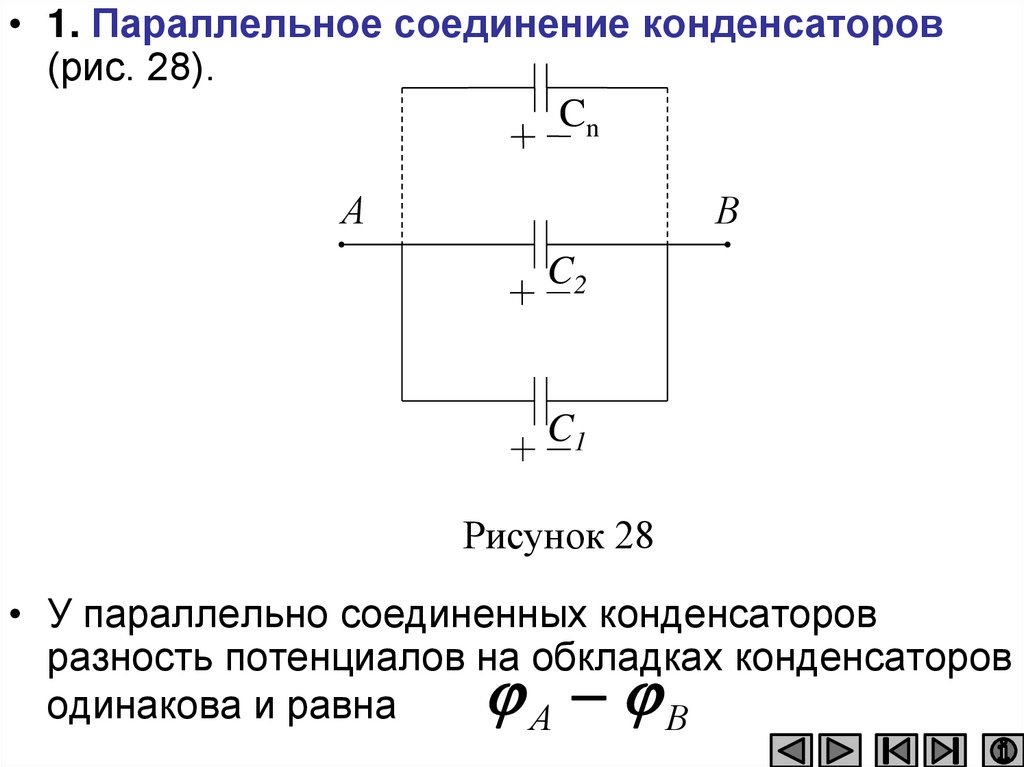




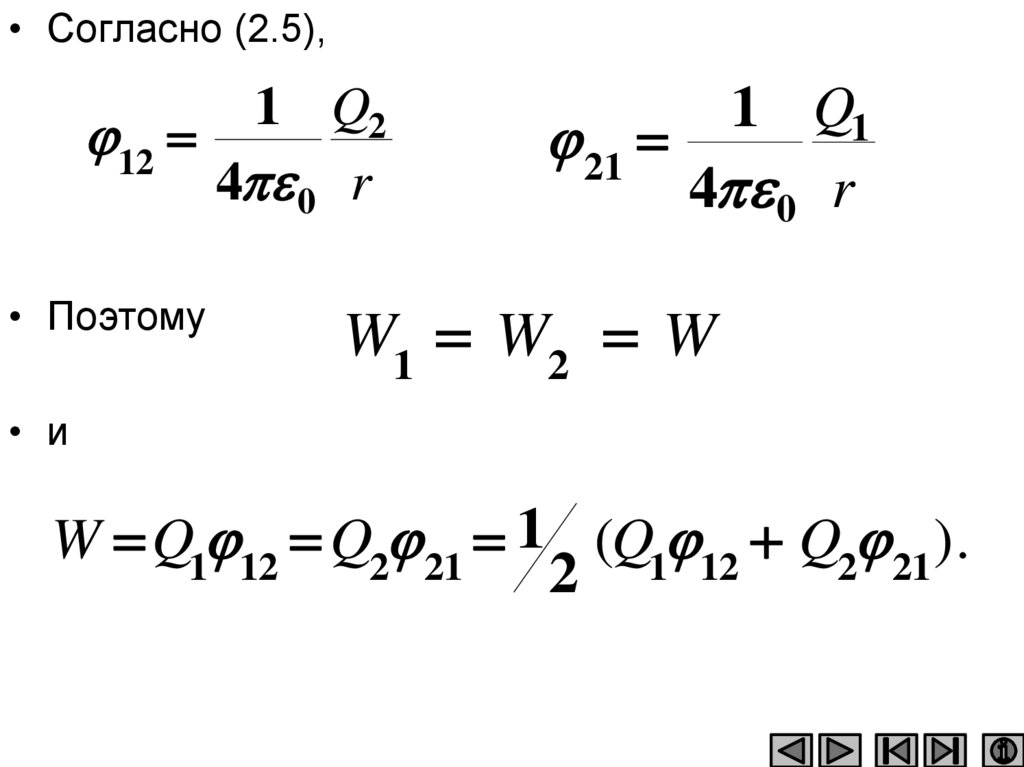








































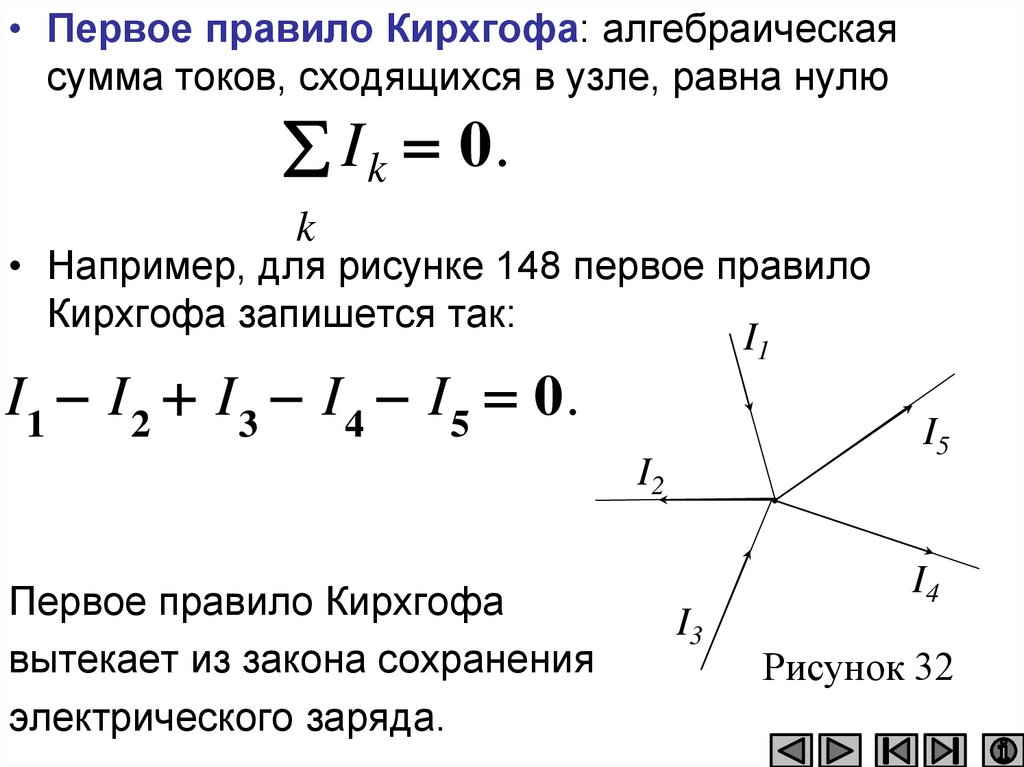































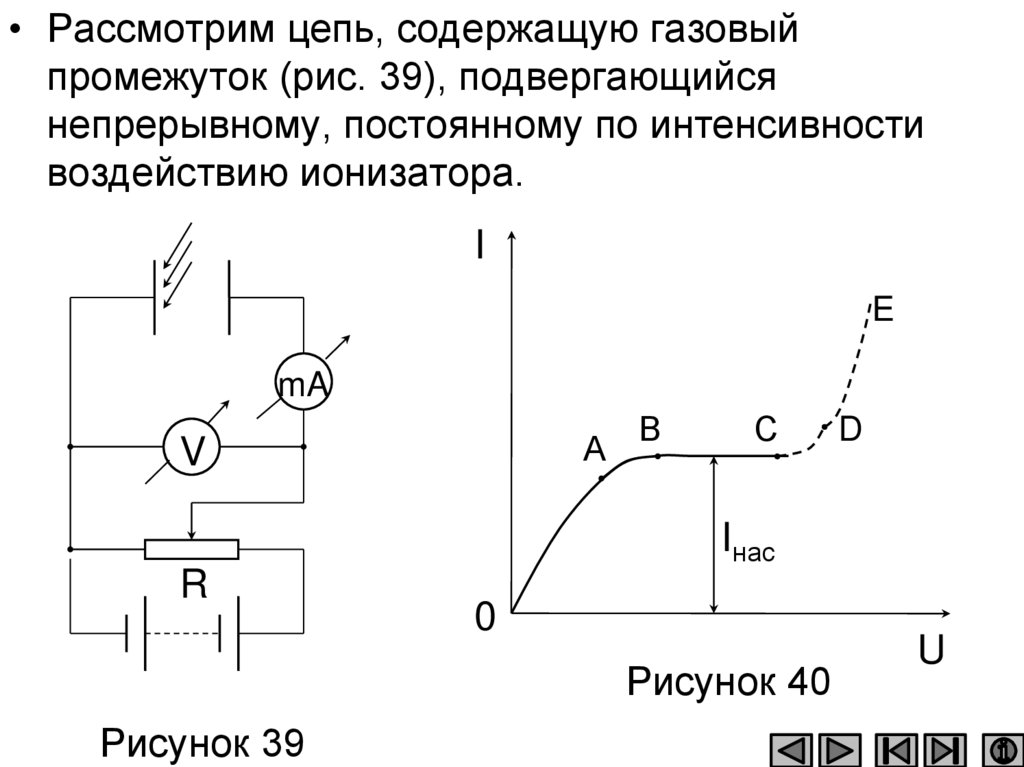







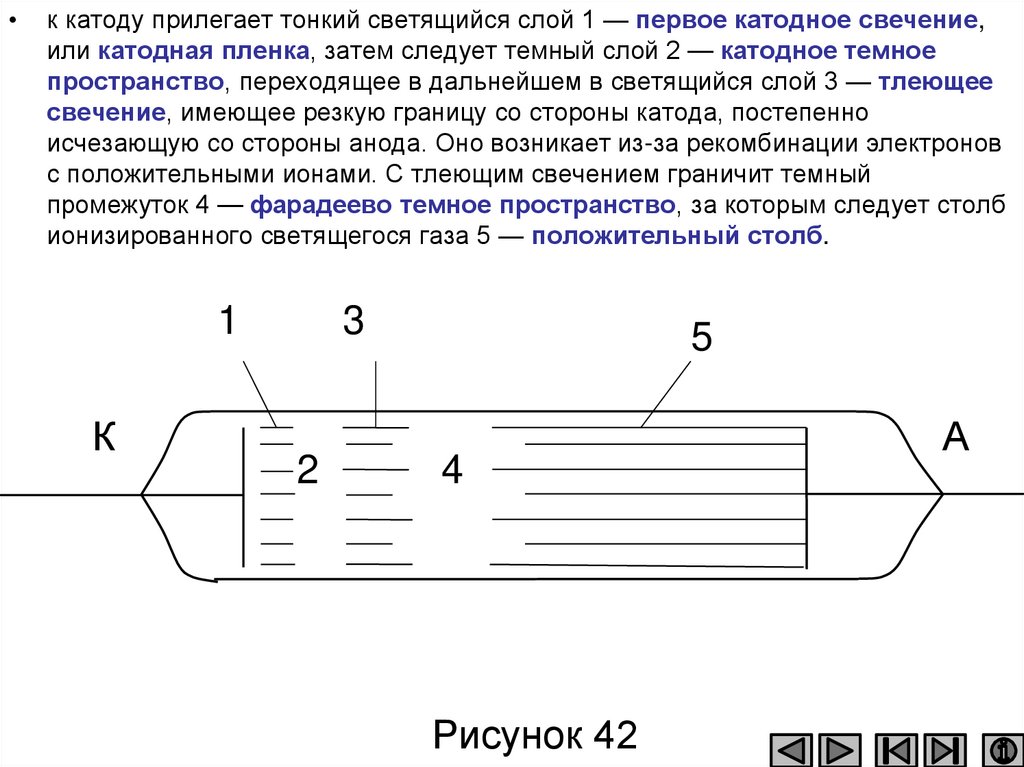





























 physics
physics








