Постоянный электрический ток

1.

Постоянный электрический ток
company name
Электрический ток
Условия существования электрического тока
Сила тока

2.

Постоянный электрический ток
Электрическим током называется направленное движение электрических
зарядов:
конвекционный (переносной) ток – это перемещение заряженных тел в
пространстве,
ток проводимости – это движение микроскопических носителей заряда
внутри неподвижного проводника,
ток в вакууме – это движение микроскопических носителей заряда в
вакууме (например, в электронной лампе).
company name
Для существования электрического тока проводимости необходимо:
наличие свободных носителей заряда – электронов, ионов
наличие в проводнике электрического поля, энергия которого
затрачивалась бы на перемещение зарядов
для длительного существования электрического тока необходим
источник тока, преобразующий какой-либо вид энергии в энергию
электрического поля.
Сила тока – скалярная величина, численно равная
электрическому заряду, проходимому через поперечное
сечение проводника за 1 с.
I 1 А
I
dq
dt

3.

Постоянный электрический ток
Постоянный ток – ток, величина и направление которого не
меняются с течением времени.
Направление постоянного тока – это направление движения
положительных зарядов.
Рассмотрим проводник, по которому течет ток.
dq
I
dt
За промежуток времени dt через поперечное
сечение
S
проводника
пройдет
число
заряженных частиц N, находящихся в некотором
объеме:
N nSVн dt ,
n – концентрация заряженных частиц, Vн –
скорость их направленного движения (дрейфа).
company name
I
Общий заряд этих частиц:
тогда сила тока
I
dq qnSVн dt ,
dq
qnSVн .
dt
Сила тока зависит от заряда, переносимого каждой частицей,
концентрации частиц, скорости их направленного движения и площади
поперечного сечения проводника.

4.

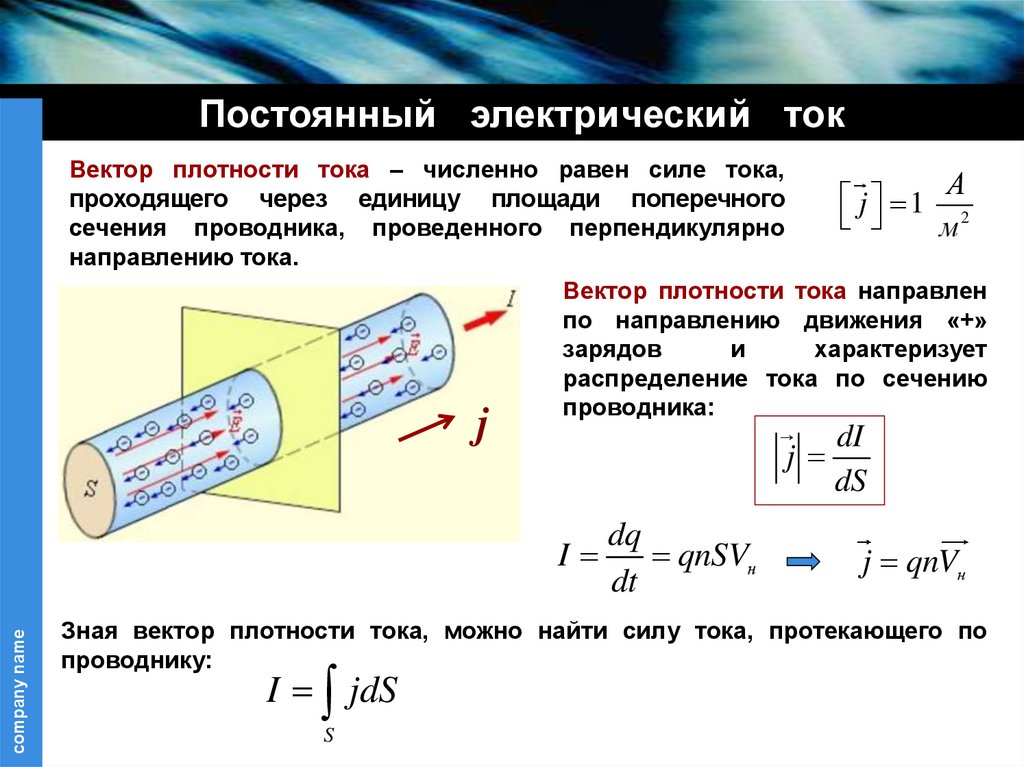
Постоянный электрический ток
Вектор плотности тока – численно равен силе тока,
проходящего через единицу площади поперечного
j 1 А2
сечения проводника, проведенного перпендикулярно
м
направлению тока.
Вектор плотности тока направлен
по направлению движения «+»
зарядов
и
характеризует
распределение тока по сечению
проводника:
j
j
company name
dq
I
qnSVн
dt
dI
dS
j qnVн
Зная вектор плотности тока, можно найти силу тока, протекающего по
проводнику:
I jdS
S

5.

Постоянный электрический ток
Электродвижущая сила
Разность потенциалов
Напряжение
1) Разность потенциалов
Работа, совершаемая силами электростатического поля (кулоновскими
силами) по перемещению единичного положительного заряда из точки 1 в
точку 2 электрической цепи называется разностью потенциалов на данном
участке цепи:
2
к
A1,2
Fк dl ,
Fк qEк
1
2
к
A1,2
q Eк dl q 1 2 q 1,2
company name
1
к
2
A1,2
1,2
EК dl
q
1
Кулоновские силы не могут обеспечить постоянный
ток. Действие кулоновских сил приводит к
выравниванию потенциалов, поле в проводнике
исчезает.
Дж
В
Кл

6.

Постоянный электрический ток
2) Электродвижущая сила - эдс
Работа, совершаемая сторонними силами (не кулоновскими силами), по
перемещению единичного положительного заряда из точки 1 в точку 2
электрической цепи называется эдс на данном участке цепи:
2
ст
A1,2
F ст dl ,
F ст qE ст
1
ст
2
2
A1,2
1
1
1,2
F ст dl qE ст dl
q
q1
q1
company name
2
1,2 E ст dl
1
Сторонние силы – это силы неэлектрической
природы. Сторонние силы разделяют разноименные
заряды (кулоновские силы соединяют разноименные
заряды). Сторонние силы обеспечивают постоянный
ток.
В

7.

Постоянный электрический ток
3) Падение напряжения, напряжение
Работа, совершаемая кулоновскими и сторонними силами вместе по
перемещению единичного положительного заряда из точки 1 в точку 2
электрической цепи называется падением напряжения (напряжение) на
данном участке цепи:
2
Fк qEк
F ст qE ст
A1,2 F к F ст dl ,
1
company name
2
2
A1,2 1 2
U1,2
qE к qE ст dl E к dl E ст dl 1,2 1,2
q
q1
1
1
U1,2 1,2 1,2
Участок цепи, на котором нет сторонних сил, называется однородным. На
однородном участке
U
1,2
1,2

8.

Постоянный электрический ток
Закон Ома для участка и полной замкнутой цепи
Сила тока, текущего по однородному металлическому
проводнику, пропорциональна падению напряжения на
проводнике:
U
I
R
(1826 г.)
R - электрическое сопротивление проводника
R 1 Ом
1В
1А
Ом Георг Симон
(1787-1854 г.)
Сопротивление металлического проводника зависит от
его размеров и материала, из которого он изготовлен:
company name
длина проводника
Немецкий физик.
Экспериментально и
теоретически открыл
основной закон эл. цепи,
ввел понятие эдс, падения
напряжения, проводимости.
l
R
S
удельное
сопротивление
площадь
поперечного
сечения проводника

9.

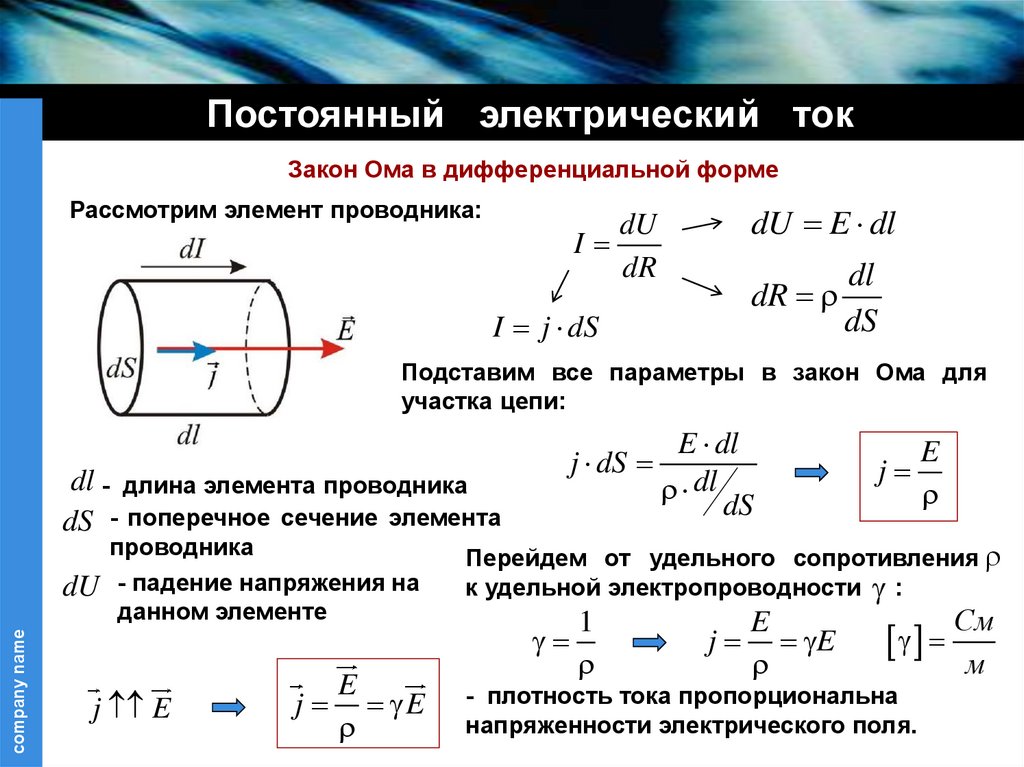
Постоянный электрический ток
Закон Ома в дифференциальной форме
Рассмотрим элемент проводника:
I
I j dS
dU
dR
dU E dl
dR
dl
dS
Подставим все параметры в закон Ома для
участка цепи:
dl - длина элемента проводника
dS - поперечное сечение элемента
company name
проводника
dU - падение напряжения на
данном элементе
j E
E
j E
E dl
j dS
dl
dS
j
E
Перейдем от удельного сопротивления
к удельной электропроводности :
1
E
j E
См
м
- плотность тока пропорциональна
напряженности электрического поля.

10.

Постоянный электрический ток
Закон Ома для неоднородного участка цепи
В общем случае на заряды могут действовать как
кулоновские, так и сторонние силы.
Напряженность результирующего силового поля
равна сумме напряженностей поля кулоновских и
поля сторонних сил:
E E к E ст
E
j
E
company name
j
1
E к E ст
1
1
E к dl E ст dl
I dl E к dl E ст dl
S
j dl
dl
j dl j dl
Интегрируем от точки 1 до точки 2 электрической цепи:
I
dl
S

11.

Закон Ома для неоднородного участка цепи
Интегрируем от точки 1 до точки 2 электрической цепи:
I dl E к dl E ст dl
1 S
1
1
2
R
2
2
1 2
1,2
IR 1 2 1,2
company name
Если цепь замкнута, то 1 2 ,
Rполн R r
R - внешнее сопротивление
r - внутреннее сопротивление
(сопротивление источника тока)
- эдс источника тока
I
R r
1 2 1,2
I
R

12.

Соединения резисторов
Последовательное соединение
n
U U i
i 1
1
I
n
R Ri
n
U
U
i
I
i 1 I
i 1
Параллельное соединение
n
I Ii
company name
i 1
1
U
n
I
I
I 1
i ,
U i 1 U
U R
n
1
1
R i 1 Ri
Величина, обратная полному сопротивлению параллельно соединенных
резисторов, равна алгебраической сумме величин их обратных
сопротивлений.

13.

Правила Кирхгофа для разветвленных цепей
Первое правило: алгебраическая сумма токов, сходящихся в в узле равна
нулю.
n
I 0
i 1
i
Узел – точка эл. схемы, в которой сходится более
двух проводников.
I1 I 2 I 3 I 4 I 5 0
company name
Токи, втекающие в узел берутся со знаком «+», токи, вытекающие из узла –
со знаком «-».
Второе правило: алгебраическая сумма произведений сил токов на
сопротивления в ветвях любого замкнутого контура равна алгебраической
сумме эдс, встречающихся в этом контуре.
n
n
I R
i 1
i
i
i 1
i

14.

Правила Кирхгофа
Знаки «+» и «-» выбираются с учетом
условного положительного направления
обхода контура.
I i Ri берутся
со знаком «+», если
направление тока и обхода совпадают;
со знаком «-» , если направления тока и
обхода противоположны.
i берется со знаком «+», если над
company name
В рассматриваемой эл. цепи
можно выделить 3 замкнутых
контура:
1) AMNB
2) CABD
3) CMND
положительным зарядом в направлении
обхода совершается положительная
работа, т.е. если обход контура идет от
«-» к «+» полюсу источника тока.
I1R1 I 2 R2 1
I 3 R3 I 2 R2 2 1
I1R1 I 3 R3 2

15.

Постоянный электрический ток
Закон Джоуля-Ленца
Описывает тепловое действие тока.
Если проводники цепи неподвижны и
электрический ток постоянен, то работа
электрических сил целиком расходуется
на нагревание проводников.
A Q
A q U
q I t
Джеймс Джоуль Эмилий Ленц
(1818-1889 г.)
(1804-1865 г.)
A I U t
company name
Количество теплоты, выделяемое током в проводнике, пропорционально
силе тока, времени его прохождения и напряжению на проводнике:
Q I U t
U I R
Закон Джоуля-Ленца
форме:
в
Q I2 R t
интегральной

16.

Постоянный электрический ток
Закон Джоуля-Ленца в дифференциальной форме
Рассмотрим элемент проводника:
Количество теплоты, выделяющейся в данном
элементе проводника:
dQ I 2 dR dt
I j dS
dl
dR
dS
dl
dQ j dS
dt j 2 dS dl dt j 2 dV dt
dS
2
2
company name
Удельная тепловая мощность тока – количество теплоты, выделяющееся
в единице объема проводника в единицу времени
dQ
dV dt
Qуд j 2 ,
1
,
j E
Qуд E 2
Qуд

17.

Постоянный электрический ток
Классическая электронная теория металлов
Основные положения:
1) атомы в металлах диссоциированы на
положительные ионы и электроны,
2) носителями тока в металлах являются
свободные
электроны
(электроны
проводимости),
3) совокупность свободных электронов
проводимости в металлах обладает
Хендрик Лоренц Пауль Друде
свойствами одноатомного электронного
1853-1928 г.
1863-1906 г.
газа и называется «электронным газом».
Концентрация электронного газа:
company name
n0 1028 1029
1
м3
Средняя длина свободного пробега:
10 10 м

18.

Классическая электронная теория металлов
Средняя скорость теплового движения:
V
8kT
m
Скорость упорядоченного движения
под действием электрического поля:
Масса и заряд электрона:
m 9,11 10 31 кг
U
e 1,6 10 19 Кл
Средняя скорость теплового движения при T=300 K :
company name
8kT
8 1,38 10 23 300
5 м
V
10
m
3,14 9,11 10 31
с
Среднюю скорость упорядоченного движения рассчитываем по плотности
тока.
Рассмотрим элемент длины проводника.

19.

Классическая электронная теория металлов
Рассмотрим элемент длины проводника.
j
I
S
I
dq
dt
j
dq e n0 S dl
1 n0eSUdt
S
dt
j n0eU
dl U dt
Среднюю скорость упорядоченного движения рассчитываем по плотности
тока.
1
Медный проводник
n 1029
j n eU
м3
А
jmax 107 2
м
company name
0
107
3 м
U 29
10
10 1,6 10 19
с
0
j
U
n0 e
U
V

20.

Классическая электронная теория металлов
Опыт Толмена и Стюарта (1916 г.)
При торможении быстро движущегося металлического
носители тока должны продолжать двигаться по инерции.
проводника
В опыте Толмена и Стюарта
резко тормозилась
вращающаяся с большой скоростью катушка. При резком
торможении быстро вращающейся катушки возникает
импульс тока за счет движения по инерции носителей
тока.
При торможении катушки на носители тока действуют
силы инерции:
company name
F ин ma m
dV
dt
При торможении вращающейся катушки
носители
тока
должны
продолжать
двигаться по инерции. Работа сил
инерции описывается эдс:
Длина провода – 500 м,
линейная скорость витков – 300 м/с.
1
m dV
F
L
ин dl
qL
q dt

21.

Классическая электронная теория металлов
По закону Ома для замкнутой цепи:
I
Протекающий по цепи заряд:
m L dV
R q R dt
0
m L dV
mL
dt
V0
q R
V0 q R dt
Q Idt
q
L V0
m
QR
company name
По результатам измерений был определен удельный заряд носителей
тока:
q
Кл
1,6 1011
m
кг
Опыт Толмена и Стюарта показал, что носителями тока в металлах
являются свободные электроны.

22.

Классическая электронная теория металлов
Закон Ома в классической теории металлов
j n0 e U ,
U 0 U max
U
2
U0 0
- время пробега
F
a , F e E
m
U 0 , U max
U max a
Электрическое
сопротивление
металлов
обусловлено
соударениями
свободных
электронов с ионами в узлах
кристаллической решетки.
eE
U
,
2m
V
eE
U
2mV
- скорости эл. поля после и перед соударением
company name
m, q - масса, заряд
Сопоставим полученное выражение с законом Ома в дифференциальной
форме:
eE
j n0 e U , U
2mV
n0e 2
j
E , j E
2mV
n0e 2
2mV

23.

Классическая электронная теория металлов
n0e 2
2mV
Полученное выражение согласуется с экспериментом:
а)
растет с ростом концентрации свободных электронов n0
и длины свободного пробега ,
б) проводимость
падает с ростом температуры T .
V
T
1
T
Закон Джоуля-Ленца в классической теории металлов
U max a
company name
eE
a
,
m
V
eE
U max
mV
При столкновениях с ионами решетки электроны
теряют
набранную
скорость
упорядоченного
движения и передают решетке приобретенную между
столкновениями кинетическую энергию.
Энергия, передаваемая решетке при однократном
столкновении одного электрона с ионом:
2
mU max
1 e 2 E 2 2
Wк
2
2 mV 2

24.

Классическая электронная теория металлов
Частота столкновений каждого электрона:
1 V
Следовательно, энергия выделяемая в единичном объеме проводника в
единицу времени, т.е. тепловая мощность тока равна:
Qуд n0
n0e 2
2mV
V
ne 2
Wк 0
E E 2
2mV
2
Закон Видемана-Франца
Для всех металлов отношение коэффициента
теплопроводности k и коэффициента удельной
электропроводимости
приблизительно
одинаково
и
изменяется
пропорционально
абсолютной температуре: k
company name
При
комнатной
(T=300 K)
const
температуре
(1853 г.)
k
Дж Ом
6 10 6
с К

25.

Классическая электронная теория металлов
Объяснение:
теплопроводность
металлов
также,
как
и
электропроводность, осуществляется в основном, за счет движения
свободных электронов.
Оценим величину коэффициента теплопроводности для электронного газа
в металлах:
1
cv
k n0 m V , - молярная масса электронного газа
3
Молярная теплоемкость электронного газа (как для одноатомного газа) при
постоянном объеме:
cv
3
3
R Na k
2
2
Na m
m - масса электрона
company name
После подстановки получаем:
1
3 Na k
k n0 m V
3
2 Na m
1
k n0 k V
2
Сравним коэффициенты теплопроводности и электропроводности:

26.

Классическая электронная теория металлов
Сравним коэффициенты теплопроводности и электропроводности:
1
k n0 k V ,
2
2
mV
3
kT
2
2
При T=300 K:
n0e
2mV
2
2
k
k
3 T
e
1
2
n
kV
0
k 2
kmV
n0e 2
e2
2m
2
1,38 10 23
k
6 Дж Ом
3
300
6,
7
10
19
1,
6
10
с К
company name
Противоречия классической теории металлов
а) точный расчет средней скорости с учетом распределения Максвелла
электронов по скоростям ухудшает согласие теории с экспериментом.
Например, в законе Видемана-Франца
2
k
k
2 T
e

27.

Классическая электронная теория металлов
б) классическая электронная теория металлов дает неправильную
зависимость сопротивления от температуры:
n0e 2
2mV
company name
1
T
8kT
V
T
m
1
теор
T
эксп
T
Зависимость сопротивления металлов от температуры:
а) экспериментальная
б) по классической теории

28.

Классическая электронная теория металлов
в) расчет длины свободного пробега электронов в электронном газе по
экспериментальным значениям электропроводности дает неожиданно
большие значения:
2
n0e
2mV
2mV
n0e2
102 103 d
d - расстояние между узлами решетки
г) трудности при подсчете теплоемкости металлов.
В молярную теплоемкость металлов дают вклад ионы решетки и
электронный газ:
теор
cмет
c реш cэл.газ
company name
c реш 3R
Ионы решетки обладают тремя
колебательными
степенями
свободы i 2i
кол
c
теор
мет
3
cэл.газ R
2
i
c R
2
Электронный
газ
(i=3)
одноатомный идеальный газ
3
3R R 4,5R
2
–

29.

Классическая электронная теория металлов
c
теор
мет
3
3R R 4,5R - теория
2
эксп
cмет
3R
- эксперимент
Закон Дюлонга-Пти
company name
Закон Дюлонга-Пти означает практическое отсутствие теплоемкости
электронного газа, т.е. при нагревании металла энергия теплового
движения электронов проводимости не изменяется???